6.4平面向量的应用-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案)
文档属性
| 名称 | 6.4平面向量的应用-【新教材】2020--2021学年人教A版(2019)高中数学必修第二册同步练习(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 58.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 00:00:00 | ||
图片预览

文档简介
1285875-3028956.4平面向量的应用
6.4平面向量的应用
1.在 △ABC 中,角 A,B,C 的对边分别为 a,b,c ,已知 c=25 ,且 2asinCcosB=asinA?bsinB+ 52bsinC ,点 O 满足 OA+OB+OC=0 , cos∠CAO=38 ,则 △ABC 的面积为(? ????)
A.?553?????????????????????????????????????B.?35?????????????????????????????????????C.?52?????????????????????????????????????D.?55
2.已知 △ABC 中, a=1,b=3,∠A=30? ,则 ∠B 等于(??? )
A.?30°???????????????????????????????B.?30°或150°???????????????????????????????C.?60°???????????????????????????????D.?60°或120°
3.已知△ABC的面积是 S=14(b2+c2) (其中b,c为△ABC的边长),则△ABC的形状为(?? )
A.?等边三角形?????????????????????????????????????????????????????????B.?是直角三角形但不是等腰三角形
C.?是等腰三角形但不是直角三角形?????????????????????????D.?等腰直角三角形
4.在△ABC中, AB=3,AC=2,BC=10 ,则 AB?AC= (??? )
A.??32???????????????????????????????????????B.??23???????????????????????????????????????C.?32???????????????????????????????????????D.?23
5.在△ABC中,A= 60° ,a=1,则 csinC= (???? )
A.?833?????????????????????????????????B.?? 2393?????????????????????????????????C.?? 233?????????????????????????????????D.?? 23 ?
6.△ABC中,角A、B、C的对边分别是a、b、c,若 a2+b2>c2 ,则三角形为( )
? A.?锐角三角形??????????????????????B.?直角三角形??????????????????????C.?钝角三角形??????????????????????D.?无法作出判断
7.向量 a , b 满足 |a|=|b|=a?b=2 ,则 |λb?a|+|λb?a2| ( λ∈R )的最小值为(????? )
A.?6??????????????????????????????????B.?7??????????????????????????????????C.?1+3??????????????????????????????????D.?12+132
8.在 △ABC 中, a , b , c 分别为 ∠A , ∠B , ∠C 的对边,如果 sinAsinB?sinC=b+cb?a ,那么 cosC 的值为(??? )
A.?12????????????????????????????????????????B.?22????????????????????????????????????????C.?23????????????????????????????????????????D.?32
9.我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜.其小斜一十三里,中斜一十四里,大斜一十五里.里法三百步.欲知为田几何.”题意是有一个三角形的沙田,其三边长分别为13里、14里、15里、1里为300步,设6尺为1步,1尺=0.231米,则该沙田的面积约为(??? )(结果精确到0.1,参考数据: 415.82=172889.64 )
A.?15.6平方千米?????????????????B.?15.2平方千米?????????????????C.?14.8平方千米?????????????????D.?14.5平方千米
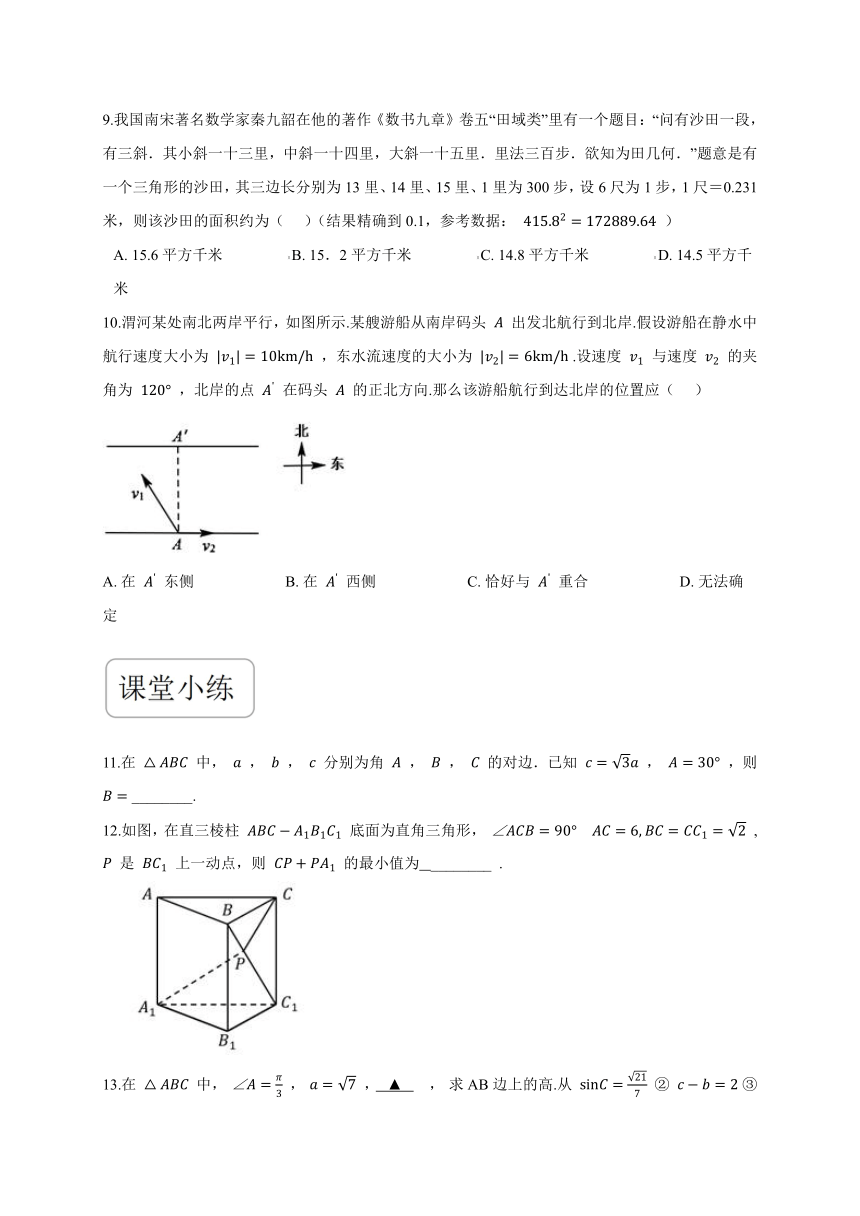
10.渭河某处南北两岸平行,如图所示.某艘游船从南岸码头 A 出发北航行到北岸.假设游船在静水中航行速度大小为 |v1|=10km/h ,东水流速度的大小为 |v2|=6km/h .设速度 v1 与速度 v2 的夹角为 120° ,北岸的点 A' 在码头 A 的正北方向.那么该游船航行到达北岸的位置应(??? )
A.?在 A' 东侧????????????????????????B.?在 A' 西侧????????????????????????C.?恰好与 A' 重合????????????????????????D.?无法确定
11.在 △ABC 中, a , b , c 分别为角 A , B , C 的对边.已知 c=3a , A=30° ,则 B= ________.
12.如图,在直三棱柱 ABC?A1B1C1 底面为直角三角形, ∠ACB=90° AC=6,BC=CC1=2 , P 是 BC1 上一动点,则 CP+PA1 的最小值为? ________??.
?
13.在 △ABC 中, ∠A=π3 , a=7 ,? ▲? , 求AB边上的高.从 sinC=217 ② c?b=2 ③ S△ABC=332 ,这三个条件中任选一个,补充在上面问题中并作答.
14.已知A、B、C为△ABC的三个内角,它们的对边分别为a、b、c,若 2acosA=ccosB+bcosC
(1)求A;
(2)若a= 23 ,△ABC的面积S= 3 ,求b+c的值.
15.已知向量 m=(3sinx,cosx?1) , n=(cosx,cosx+1) .若 f(x)=m?n .
(1)求函数 f(x) 的单调递增区间;
(2)在 Rt△ABC 中,角 A , B , C 的对边分别为 a , b , c ,若 ∠A=90° , f(C)=0 , c=3 , CD 为 ∠BCA 的角平分线, E 为 CD 中点,求 BE 的长.
1.【答案】 D 2.【答案】 D 3.【答案】 D 4.【答案】 C 5.【答案】 C 6.【答案】 D 7.【答案】 B 8.【答案】 A 9.【答案】 D 10.【答案】 A
11.【答案】 90°或30° 12.【答案】 52
13.【答案】 选择①:
在 △ABC 中,由正弦定理 asinA=csinC ,
得 732=c217 ,所以 c=2 ,
由余弦定理 a2=b2+c2?2bccosA ,
得 72=b2+22?2×2×b×12 ,
b2?2b?3=0 ,解得 b=3 ,
AB 边上的高 ?=bsinA=3×32=332 .
选择②:在 △ABC 中,由 c?b=2 ,得 c=b+2 ,
由余弦定理 a2=b2+c2?2bccosA ,
得 72=b2+(b+2)2?2×(b+2)×b×12 ,
化简 b2+2b?3=0 ,解得 b=1 ,
AB 边上的高 ?=bsinA=3×32=332 .
选择③:
在 △ABC 中,由 S△ABC=12bcsinA=332 ,
得 12bc?32=332 ,所以 bc=6 ,
由余弦定理 a2=b2+c2?2bccosA ,
得 a2=(b+c)2?2bc?2bccosA ,
72=(b+c)2?12?12×12 ,
解得 b+c=5 ,
所以 {b=2c=3 或 {b=3c=2 ,
AB 边上的高 ?=bsinA=3×32=332
14.【答案】 (1)由正弦定理得; 2sinAcosA=sinCcosB+sinBcosC ?
所以 2sinAcosA=sin(B+C)=sinA
由于 sinA≠0 ,所以 2cosA=1 ,即 cosA=12
因为0(2)因为 SΔ=12bcsinπ3=3,则bc=4
由余弦定理知: a2=b2+c2?2bccosAa2=(b+c)2?2bc(1+cosA)
所以 (b+c)2=a2+2bc(1+cosA)=12+2×4×(1+12)=24
所以 b+c=26
15.【答案】 (1)解: f(x)=m?n=3sinx?cosx+cos2x?1
=32sin2x+12cos2x?12 =sin(2x+π6)?12
函数 f(x) 的单调递增区间 2x+π6∈[2kπ?π2,2kπ+π2](k∈Z)
x∈[kπ?π3,kπ+π6](k∈Z)
(2)解: f(C)=sin(2C+π6)?12=0
sin(2C+π6)=12 , C∈(0,π2) ,所以 C=π3
在 ΔACD 中: CD=233
在 ΔBCE 中: BE=22+(33)2?2×2×33×32=213 .
6.4平面向量的应用
1.在 △ABC 中,角 A,B,C 的对边分别为 a,b,c ,已知 c=25 ,且 2asinCcosB=asinA?bsinB+ 52bsinC ,点 O 满足 OA+OB+OC=0 , cos∠CAO=38 ,则 △ABC 的面积为(? ????)
A.?553?????????????????????????????????????B.?35?????????????????????????????????????C.?52?????????????????????????????????????D.?55
2.已知 △ABC 中, a=1,b=3,∠A=30? ,则 ∠B 等于(??? )
A.?30°???????????????????????????????B.?30°或150°???????????????????????????????C.?60°???????????????????????????????D.?60°或120°
3.已知△ABC的面积是 S=14(b2+c2) (其中b,c为△ABC的边长),则△ABC的形状为(?? )
A.?等边三角形?????????????????????????????????????????????????????????B.?是直角三角形但不是等腰三角形
C.?是等腰三角形但不是直角三角形?????????????????????????D.?等腰直角三角形
4.在△ABC中, AB=3,AC=2,BC=10 ,则 AB?AC= (??? )
A.??32???????????????????????????????????????B.??23???????????????????????????????????????C.?32???????????????????????????????????????D.?23
5.在△ABC中,A= 60° ,a=1,则 csinC= (???? )
A.?833?????????????????????????????????B.?? 2393?????????????????????????????????C.?? 233?????????????????????????????????D.?? 23 ?
6.△ABC中,角A、B、C的对边分别是a、b、c,若 a2+b2>c2 ,则三角形为( )
? A.?锐角三角形??????????????????????B.?直角三角形??????????????????????C.?钝角三角形??????????????????????D.?无法作出判断
7.向量 a , b 满足 |a|=|b|=a?b=2 ,则 |λb?a|+|λb?a2| ( λ∈R )的最小值为(????? )
A.?6??????????????????????????????????B.?7??????????????????????????????????C.?1+3??????????????????????????????????D.?12+132
8.在 △ABC 中, a , b , c 分别为 ∠A , ∠B , ∠C 的对边,如果 sinAsinB?sinC=b+cb?a ,那么 cosC 的值为(??? )
A.?12????????????????????????????????????????B.?22????????????????????????????????????????C.?23????????????????????????????????????????D.?32
9.我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜.其小斜一十三里,中斜一十四里,大斜一十五里.里法三百步.欲知为田几何.”题意是有一个三角形的沙田,其三边长分别为13里、14里、15里、1里为300步,设6尺为1步,1尺=0.231米,则该沙田的面积约为(??? )(结果精确到0.1,参考数据: 415.82=172889.64 )
A.?15.6平方千米?????????????????B.?15.2平方千米?????????????????C.?14.8平方千米?????????????????D.?14.5平方千米
10.渭河某处南北两岸平行,如图所示.某艘游船从南岸码头 A 出发北航行到北岸.假设游船在静水中航行速度大小为 |v1|=10km/h ,东水流速度的大小为 |v2|=6km/h .设速度 v1 与速度 v2 的夹角为 120° ,北岸的点 A' 在码头 A 的正北方向.那么该游船航行到达北岸的位置应(??? )
A.?在 A' 东侧????????????????????????B.?在 A' 西侧????????????????????????C.?恰好与 A' 重合????????????????????????D.?无法确定
11.在 △ABC 中, a , b , c 分别为角 A , B , C 的对边.已知 c=3a , A=30° ,则 B= ________.
12.如图,在直三棱柱 ABC?A1B1C1 底面为直角三角形, ∠ACB=90° AC=6,BC=CC1=2 , P 是 BC1 上一动点,则 CP+PA1 的最小值为? ________??.
?
13.在 △ABC 中, ∠A=π3 , a=7 ,? ▲? , 求AB边上的高.从 sinC=217 ② c?b=2 ③ S△ABC=332 ,这三个条件中任选一个,补充在上面问题中并作答.
14.已知A、B、C为△ABC的三个内角,它们的对边分别为a、b、c,若 2acosA=ccosB+bcosC
(1)求A;
(2)若a= 23 ,△ABC的面积S= 3 ,求b+c的值.
15.已知向量 m=(3sinx,cosx?1) , n=(cosx,cosx+1) .若 f(x)=m?n .
(1)求函数 f(x) 的单调递增区间;
(2)在 Rt△ABC 中,角 A , B , C 的对边分别为 a , b , c ,若 ∠A=90° , f(C)=0 , c=3 , CD 为 ∠BCA 的角平分线, E 为 CD 中点,求 BE 的长.
1.【答案】 D 2.【答案】 D 3.【答案】 D 4.【答案】 C 5.【答案】 C 6.【答案】 D 7.【答案】 B 8.【答案】 A 9.【答案】 D 10.【答案】 A
11.【答案】 90°或30° 12.【答案】 52
13.【答案】 选择①:
在 △ABC 中,由正弦定理 asinA=csinC ,
得 732=c217 ,所以 c=2 ,
由余弦定理 a2=b2+c2?2bccosA ,
得 72=b2+22?2×2×b×12 ,
b2?2b?3=0 ,解得 b=3 ,
AB 边上的高 ?=bsinA=3×32=332 .
选择②:在 △ABC 中,由 c?b=2 ,得 c=b+2 ,
由余弦定理 a2=b2+c2?2bccosA ,
得 72=b2+(b+2)2?2×(b+2)×b×12 ,
化简 b2+2b?3=0 ,解得 b=1 ,
AB 边上的高 ?=bsinA=3×32=332 .
选择③:
在 △ABC 中,由 S△ABC=12bcsinA=332 ,
得 12bc?32=332 ,所以 bc=6 ,
由余弦定理 a2=b2+c2?2bccosA ,
得 a2=(b+c)2?2bc?2bccosA ,
72=(b+c)2?12?12×12 ,
解得 b+c=5 ,
所以 {b=2c=3 或 {b=3c=2 ,
AB 边上的高 ?=bsinA=3×32=332
14.【答案】 (1)由正弦定理得; 2sinAcosA=sinCcosB+sinBcosC ?
所以 2sinAcosA=sin(B+C)=sinA
由于 sinA≠0 ,所以 2cosA=1 ,即 cosA=12
因为0
由余弦定理知: a2=b2+c2?2bccosAa2=(b+c)2?2bc(1+cosA)
所以 (b+c)2=a2+2bc(1+cosA)=12+2×4×(1+12)=24
所以 b+c=26
15.【答案】 (1)解: f(x)=m?n=3sinx?cosx+cos2x?1
=32sin2x+12cos2x?12 =sin(2x+π6)?12
函数 f(x) 的单调递增区间 2x+π6∈[2kπ?π2,2kπ+π2](k∈Z)
x∈[kπ?π3,kπ+π6](k∈Z)
(2)解: f(C)=sin(2C+π6)?12=0
sin(2C+π6)=12 , C∈(0,π2) ,所以 C=π3
在 ΔACD 中: CD=233
在 ΔBCE 中: BE=22+(33)2?2×2×33×32=213 .
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
