江西省南昌市2012年中考数学研讨会资料 用思维演绎真知
文档属性
| 名称 | 江西省南昌市2012年中考数学研讨会资料 用思维演绎真知 |
|
|
| 格式 | zip | ||
| 文件大小 | 73.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-15 19:48:54 | ||
图片预览


文档简介
用思维演绎真知,追求“思考的深度,理解的宽度,演绎的缜密”数学教育之化境
【案例1】 冷静从合情思考
问 题:要购买一块绸布,宽为1米,长为a米, 用来剪出三块矩形旗帜.
要 求: 1.裁剪截出矩形旗帜的长与宽的比与原绸布的长与宽的比相同.
2.尽可能少的出现废料.
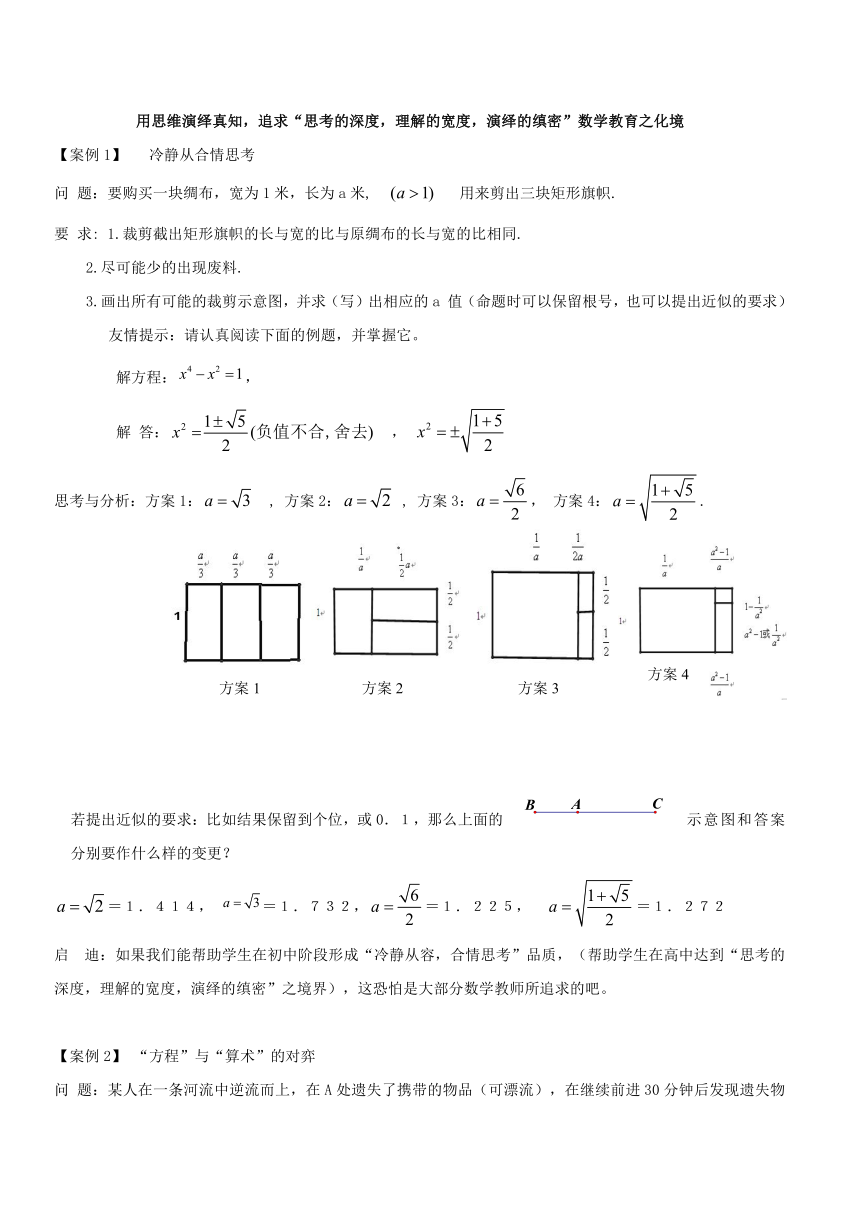
3.画出所有可能的裁剪示意图,并求(写)出相应的a 值(命题时可以保留根号,也可以提出近似的要求)
友情提示:请认真阅读下面的例题,并掌握它。
解方程:,
解 答: ,
思考与分析:方案1: , 方案2: , 方案3:, 方案4:.
若提出近似的要求:比如结果保留到个位,或0.1,那么上面的示意图和答案分别要作什么样的变更?
=1.414, =1.732,=1.225, =1.272
启 迪:如果我们能帮助学生在初中阶段形成“冷静从容,合情思考”品质,(帮助学生在高中达到“思考的深度,理解的宽度,演绎的缜密”之境界),这恐怕是大部分数学教师所追求的吧。
【案例2】 “方程”与“算术”的对弈
问 题:某人在一条河流中逆流而上,在A处遗失了携带的物品(可漂流),在继续前进30分钟后发现遗失物品,即刻顺流而下去追赶物品,在离A处3千米的B处追上物品,求水流速度.
思考与分析:(算术方法):w—人在静水中游速.v—水速
∵人离开物品的速度是w- v + v = w 人追赶物品的速度是w + v – v = w
∴人离开物品的时间=人追赶物品的时间
∴物品漂浮了1小时.∴v=3千米/时
(方程方法):AC= AB=3 BC=
启 迪:“算术方法”是“巧劲”需要学生聪慧;“方程方法”是“钝劲”需要学生踏实.
“算术方法”难想,但解决问题的过程比较巧;“方程方法”合情合理,但有可能方程难解甚至暂时解不了.
【案例3】 操作与思考
问 题:已知如图,∠BAC=100°,∠B=60°,CD平分∠ACB,∠EAC=20°,求∠DEB的度数
思考与分析:按题意画出精确地符合条件的图形,那么∠DEB的度数可用量角器测
量知道是20°,从而,可∠AED=20°.即该题只要证DE是∠AEB的角平分线就可以了.
启 迪:学生的思维状态如果滞留在“纯几何计算”的范畴里,就难以想到
通过证明DE是∠AEB的角平分线来解决问题的思路了。但是我们
平时的几何教学中,重视动手,学生有“量一量”的意识,恐怕会给
我们带来欣喜的。
【案例4】 拓宽知识放飞思维
问 题:如图,Rt△ABC中,AC=BC=3,Rt△EDC中,EC=CD=2. 绕点C顺时针旋转△ECD 60°,
得到△ECD’,过点C作CM⊥D’E’于M交AE’于N.求MN的长.
思考与分析:(解析法)点E’点D’可求,直线ED’可求,CM⊥D’E’.则CM的
斜率可求,则直线CM可求,点M可求,直线AE可求,则点N可求.
利用两点之间距离公式求出MN的长
启 迪:面向全体学生,不仅仅是,提醒我们不要抛弃一个差生,我们同样不要漠视了一大批优生的学习潜质,在合适的时候做一点合适的知识拓宽,恐怕在数学教学实践中,百分之九十的老师都是这样做的吧,但是,我还是要友情提示一下:把思维发展放在第一位,知识拓宽只是顺势而为。
【案例5】 追溯、变式、引申
问 题: 如图,给出四个不同形态的“n角星”,分别解答下面问题。
(在同一平面内,有任意三点都不在同一直线上的n个点,将每间隔k个点的两点,顺次连接起来而形成的图形,我们姑且称其为“n角星”)
在图1中,求:;
在图2中,求:;
(3)在图3中,求:
(4)图4是顺次连接每间隔k个点的两点形成的“n角星”
①求:
②写出n、k必须满足的条件
思考与分析:(略)
启 迪:请反思一下问题(1)的求解的路径
请反思一下问题(2)提出的思考的方向与问题(1)的方向有什么变化?
问题(1)是在设置好的情景中按要求解决问题,我们学会用不同的方式来解决(一题多解)。
问题(2)的提出,是研究问题的视角变化,我们要学会提出问题(一题多变)
请思考问题(3)和(4)是如何在前面两个问题的基础上进行的变化(变式与引申)
【案例5】深入浅出 搭建进步的阶梯
问 题:(1)线段AB上有一点C,AB=3,BC=1, 求AC长?
(2)A、B、C是直线上 l 的三点,AB=3, BC=1,求AC长?
(3)A、B、C是直线上 l 的三点,且 AB=a, BC=b,求AC长?
思考与分析:(略)
启 迪:让每个孩子都会去学数学,让每个孩子都不怕学数学,让每个孩子都学好数学。简单的问题,同样有浓浓的数学味。
【案例6】 尊重学生 尊重真理
问 题:如图,已知经过原点的抛物线y=-2x2+4x与x轴的另一交点为A,现将它向右平移m(m>0)个单位,所得抛物线与x轴交与C、D两点,与原抛物线交与点P.
(1)求点A的坐标,并判断△PCA存在时它的形状(不要求说理)
(2)在x轴上是否存在两条相等的线段,若存在,请一一找出,并
写出它们的长度(可用含m的式子表示);若不存在,请说明理由;
(3)△CDP的面积为S,求S关于m的关系式。
思考与分析:点A的坐标是(2,0),△PCA是等腰三角形, 存在。 OC=AD=m, OA=CD=2,
点P坐标为( , )又CD=2,
当
当
当
(这时,即指点P在X轴上PCD的面积为0)
启 迪:这个问题大家很熟悉,但是解答与标准答案不一样,我们千万不能用自己的思维定势去束缚学生的发展。
方案1
方案2
方案3
方案4
图1
图2
【案例1】 冷静从合情思考
问 题:要购买一块绸布,宽为1米,长为a米, 用来剪出三块矩形旗帜.
要 求: 1.裁剪截出矩形旗帜的长与宽的比与原绸布的长与宽的比相同.
2.尽可能少的出现废料.
3.画出所有可能的裁剪示意图,并求(写)出相应的a 值(命题时可以保留根号,也可以提出近似的要求)
友情提示:请认真阅读下面的例题,并掌握它。
解方程:,
解 答: ,
思考与分析:方案1: , 方案2: , 方案3:, 方案4:.
若提出近似的要求:比如结果保留到个位,或0.1,那么上面的示意图和答案分别要作什么样的变更?
=1.414, =1.732,=1.225, =1.272
启 迪:如果我们能帮助学生在初中阶段形成“冷静从容,合情思考”品质,(帮助学生在高中达到“思考的深度,理解的宽度,演绎的缜密”之境界),这恐怕是大部分数学教师所追求的吧。
【案例2】 “方程”与“算术”的对弈
问 题:某人在一条河流中逆流而上,在A处遗失了携带的物品(可漂流),在继续前进30分钟后发现遗失物品,即刻顺流而下去追赶物品,在离A处3千米的B处追上物品,求水流速度.
思考与分析:(算术方法):w—人在静水中游速.v—水速
∵人离开物品的速度是w- v + v = w 人追赶物品的速度是w + v – v = w
∴人离开物品的时间=人追赶物品的时间
∴物品漂浮了1小时.∴v=3千米/时
(方程方法):AC= AB=3 BC=
启 迪:“算术方法”是“巧劲”需要学生聪慧;“方程方法”是“钝劲”需要学生踏实.
“算术方法”难想,但解决问题的过程比较巧;“方程方法”合情合理,但有可能方程难解甚至暂时解不了.
【案例3】 操作与思考
问 题:已知如图,∠BAC=100°,∠B=60°,CD平分∠ACB,∠EAC=20°,求∠DEB的度数
思考与分析:按题意画出精确地符合条件的图形,那么∠DEB的度数可用量角器测
量知道是20°,从而,可∠AED=20°.即该题只要证DE是∠AEB的角平分线就可以了.
启 迪:学生的思维状态如果滞留在“纯几何计算”的范畴里,就难以想到
通过证明DE是∠AEB的角平分线来解决问题的思路了。但是我们
平时的几何教学中,重视动手,学生有“量一量”的意识,恐怕会给
我们带来欣喜的。
【案例4】 拓宽知识放飞思维
问 题:如图,Rt△ABC中,AC=BC=3,Rt△EDC中,EC=CD=2. 绕点C顺时针旋转△ECD 60°,
得到△ECD’,过点C作CM⊥D’E’于M交AE’于N.求MN的长.
思考与分析:(解析法)点E’点D’可求,直线ED’可求,CM⊥D’E’.则CM的
斜率可求,则直线CM可求,点M可求,直线AE可求,则点N可求.
利用两点之间距离公式求出MN的长
启 迪:面向全体学生,不仅仅是,提醒我们不要抛弃一个差生,我们同样不要漠视了一大批优生的学习潜质,在合适的时候做一点合适的知识拓宽,恐怕在数学教学实践中,百分之九十的老师都是这样做的吧,但是,我还是要友情提示一下:把思维发展放在第一位,知识拓宽只是顺势而为。
【案例5】 追溯、变式、引申
问 题: 如图,给出四个不同形态的“n角星”,分别解答下面问题。
(在同一平面内,有任意三点都不在同一直线上的n个点,将每间隔k个点的两点,顺次连接起来而形成的图形,我们姑且称其为“n角星”)
在图1中,求:;
在图2中,求:;
(3)在图3中,求:
(4)图4是顺次连接每间隔k个点的两点形成的“n角星”
①求:
②写出n、k必须满足的条件
思考与分析:(略)
启 迪:请反思一下问题(1)的求解的路径
请反思一下问题(2)提出的思考的方向与问题(1)的方向有什么变化?
问题(1)是在设置好的情景中按要求解决问题,我们学会用不同的方式来解决(一题多解)。
问题(2)的提出,是研究问题的视角变化,我们要学会提出问题(一题多变)
请思考问题(3)和(4)是如何在前面两个问题的基础上进行的变化(变式与引申)
【案例5】深入浅出 搭建进步的阶梯
问 题:(1)线段AB上有一点C,AB=3,BC=1, 求AC长?
(2)A、B、C是直线上 l 的三点,AB=3, BC=1,求AC长?
(3)A、B、C是直线上 l 的三点,且 AB=a, BC=b,求AC长?
思考与分析:(略)
启 迪:让每个孩子都会去学数学,让每个孩子都不怕学数学,让每个孩子都学好数学。简单的问题,同样有浓浓的数学味。
【案例6】 尊重学生 尊重真理
问 题:如图,已知经过原点的抛物线y=-2x2+4x与x轴的另一交点为A,现将它向右平移m(m>0)个单位,所得抛物线与x轴交与C、D两点,与原抛物线交与点P.
(1)求点A的坐标,并判断△PCA存在时它的形状(不要求说理)
(2)在x轴上是否存在两条相等的线段,若存在,请一一找出,并
写出它们的长度(可用含m的式子表示);若不存在,请说明理由;
(3)△CDP的面积为S,求S关于m的关系式。
思考与分析:点A的坐标是(2,0),△PCA是等腰三角形, 存在。 OC=AD=m, OA=CD=2,
点P坐标为( , )又CD=2,
当
当
当
(这时,即指点P在X轴上PCD的面积为0)
启 迪:这个问题大家很熟悉,但是解答与标准答案不一样,我们千万不能用自己的思维定势去束缚学生的发展。
方案1
方案2
方案3
方案4
图1
图2
同课章节目录
