五年级上册数学课件-除数是整数的小数除法人教版(共64张PPT)
文档属性
| 名称 | 五年级上册数学课件-除数是整数的小数除法人教版(共64张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 12.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-27 00:00:00 | ||
图片预览







文档简介
(共64张PPT)
除数是整数的小数除法
经历由整数除法的计算迁移到除数是整数的小数除法计算的探究过程,理解商的小数点和被除数的小数点对齐,体会转化思想。
能正确地计算小数除以整数,进一步提高运算能力。
感受小数除以整数与生活的密切联系,培养归纳、概括的能力和良好的验算习惯。
教学目标
明确商的小数点与被除数小数点对齐的道理。
明确余数末尾添“0”继续除的道理和方法;明确首位商“0”的道理。
教学重点
教学难点
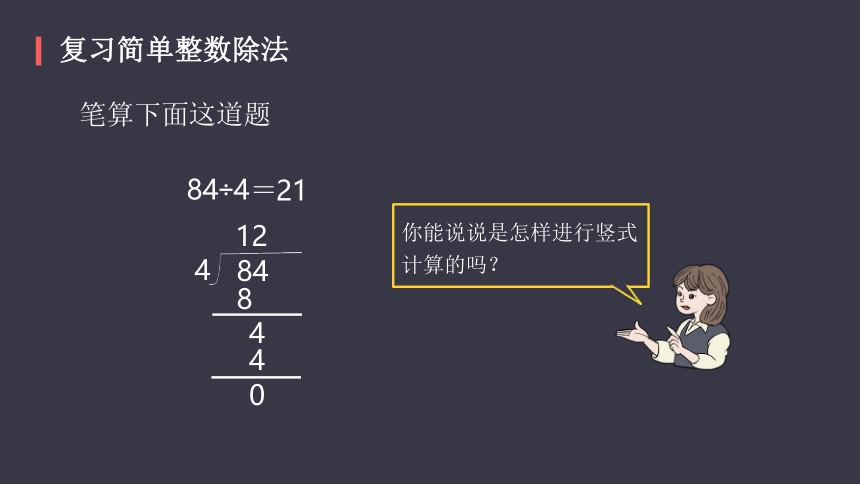
笔算下面这道题
复习简单整数除法
84÷4=
21
你能说说是怎样进行竖式计算的吗?
4
12
8
4
4
0
84
整数除法的竖式是怎样计算的?
2.
除到被除数的哪一位,就在那一
位上面写_____。
3.
求出每一位商,余下的数必须比除数
___。
王鹏的爸爸计划4个月跑步224千米,平均每个月应跑多少千米?
复习旧知
1.
从被除数的______位除起,先用除
数试除被除数的前______位数,如
果它比除数小,再试除前_____位。
最高
一
两
商
小
224÷4=
56(千米)
4
2
0
2
2
4
4
0
5
6
5个十
20个十
24个一
2
2
4
王鹏坚持晨练。他平均每周应跑多少千米?
想一想:被除数是小数该怎么除呢?
主题图导入
甲商店牛奶每袋多少元?
答:甲商店牛奶每袋2.3元。
11.5÷5=
2.3(元)
5
10
1
5
1.5
不同情境版
2
3
元
角
0
11.5
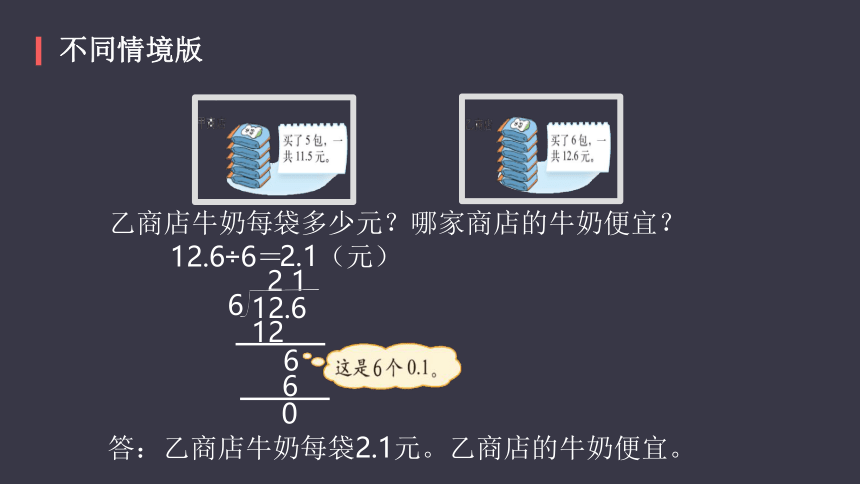
乙商店牛奶每袋多少元?哪家商店的牛奶便宜?
答:乙商店牛奶每袋2.1元。乙商店的牛奶便宜。
12.6÷6=
2.1(元)
不同情境版
12
6
6
0
2
1
6
12.6
王鹏坚持晨练。他平均每周应跑多少千米?
想一想:被除数是小数该怎么除呢?
探究新知
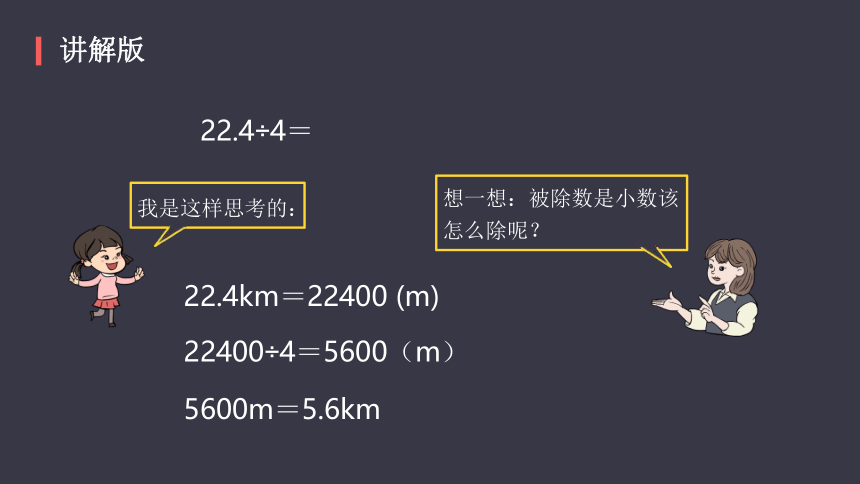
22.4÷4=
想一想:被除数是小数该怎么除呢?
我是这样思考的:
22.4km=22400
(m)
22400÷4=5600(m)
5600m=5.6km
讲解版
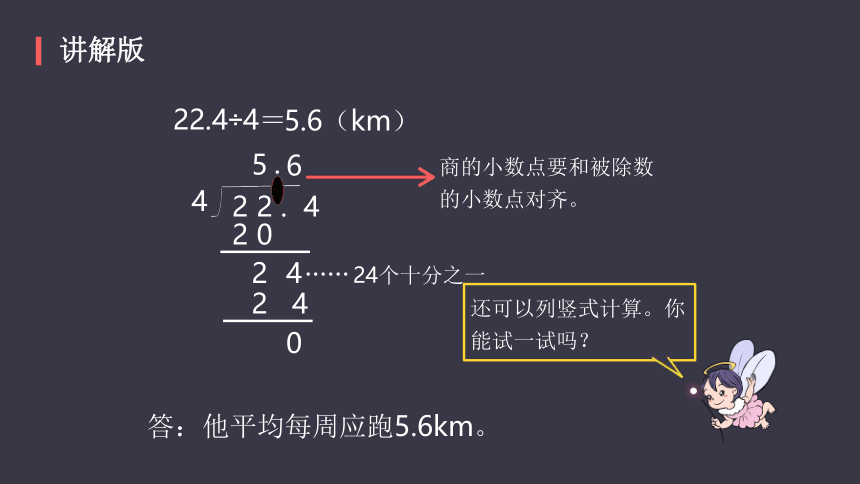
22.4÷4=
5.6(km)
商的小数点要和被除数的小数点对齐。
还可以列竖式计算。你能试一试吗?
答:他平均每周应跑5.6km。
4
2
0
4
2
2
?
4
0
5
.
讲解版
24个十分之一
……
2
2
.
4
6
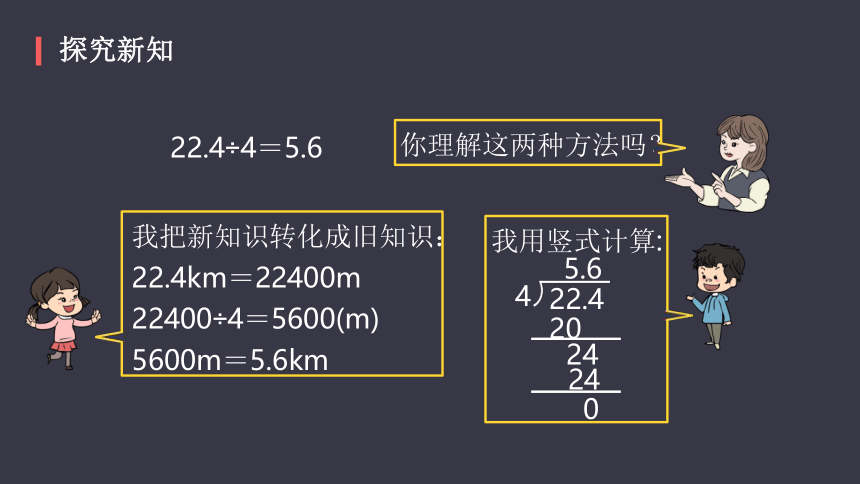
22.4÷4=5.6
你理解这两种方法吗?
我把新知识转化成旧知识:
22.4km=22400m
22400÷4=5600(m)
5600m=5.6km
我用竖式计算:
探究新知
4
20
24
24
0
5.6
22.4
42÷3=
算一算,比一比
14
4.2÷3=
1.4
相同点:小数除以整数与整数除以整数的计算方法相同。
不同点:小数除以整数要把商的小数点与被除数的小数点对齐。
想一想,这两道题有哪些相同点和不同点呢?
做一做
先想一想计算时应该注意什么,再计算。
9.6÷4=
2.4
25.2÷6=
4.2
做一做
34.5÷15=
2.3
先想一想计算时应该注意什么,再计算。
18.9÷6=
不同情境版
3.15(元)
18
3
6
9
6
3
0
3
0
0
答:每把笤帚3.15元。
买6把笤帚共花了18.9元。每把笤帚多少元?估一估,算一算。
1
.
这是5个0.01
还能算下去吗?
3个0.1可以看成30个0.01
3角就是30分
5
3
18.9
26÷4=
6.5(元)
答:每把笤帚6.5元。
6
5
4
24
20
2
0
0
.
买4个簸箕共花了26元。每个簸箕多少元?请接着算下去。
不同情境版
把余数2看成20个0.1,就能除下去了。
.
26
王鹏的爷爷计划16天慢跑28km,平均每天慢跑多少千米?
探究新知
28÷16=
把计划16天慢跑的28千米平均分成16份,每份就是爷爷一天应跑的千米数。
爷爷平均每天慢跑多少千米?
王鹏的爷爷计划16天慢跑28km,平均每天慢跑多少千米?
探究新知
12表示什么,接下来该怎么除呢?
添0继续除,表示120个(?
?
?)分之一。
十
28÷16=
1
7
16
16
12
.
0
……
28
.
0
王鹏的爷爷计划16天慢跑28km,平均每天慢跑多少千米?
计算除数是整数的小数除法要注意什么?
讲解版
添0继续除,表示120个(?
?
?)分之一。
十
28÷16=
1
7
16
16
12
.
0
……
11
2
8
0
8
0
添0继续除,表示80个(?
?
?)分之一。
……
百
0
120-112=8,8比16小,还是没有除尽,该怎么办呢?
5
0
1.75(km)
答:平均每天慢跑1.75km。
商的小数点要和被除数的小数点对齐。
如果有余数,要添0再除。
28
.
0
5.6÷7=
探究新知
我每周计划跑5.6km。
一周是7天,把每周计划跑的5.6km平均分成7份,每份就是他一天跑的千米数。
他平均每天要跑多少千米?
王鹏每周计划跑5.6km,平均每天要跑多少千米?
为什么要商0呢?
整数部分不够商1,用0补位。
答:平均每天要跑0.8km。
5.6÷7=
0.8(km)
7
5
6
0
0.
8
讲解版
5.6
讲解版
怎样验算呢?自己试一试。
5.6÷7=
0.8(km)
验算:
0.
8
×
5.
6
7
7
5
6
0
0.8
5.6
计算除数是整数的除法,要注意什么呢?
按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。
整数不够除,商0,点上小数点。如果有余数,要添0再除。
讲解版
王鹏坚持晨练。他平均每天要跑多少千米?
总结版
我计划每周跑步5.6千米。
计划每周跑步5.6千米,平均每天要跑多少千米?
总结版
5.6
÷7=?
_____(千米)
0.8
整数部分不够商1时,先在商的个位上写0,点上小数点后再除。
5.6
0
8
.
7
5
6
0
当除到有余数的时候,可以在余数的末尾补“0”,然后再继续除。因为小数的末尾添0或者去掉0,小数的大小不变。
1
2
60
6
0
1
2
0
0.1
5
总结版
1.8
按照整数除法的方法计算;商的小数点与被除数的小数点对齐;
整数部分不够除,商0,点上小数点。
除到有余数时,添0再除。
总结版
?
5.6
22.4
20
?
24
?
24
?
?
0
4
0.15
1.8
1
2
?
?60
?
?60
?
?
?0
12
列竖式计算
做一做
72
÷15=
25.5÷6=
4.8
4.25
0.54÷6=
0.09
86
÷
16=
5.375
0.416÷32=
0.013
14.21÷7=
2.03
7.83÷9=
0.87
6.3÷14=
0.45
1.26÷28=
0.045
42÷3=
算一算,比一比
14
4.2÷3=
1.4
84÷4=
8.4÷4=
21
2.1
91÷14=
9.1÷14=
6.5
0.65
相同点:小数除以整数与整数除以整数的计算方法相同。
不同点:小数除以整数要把商的小数点和被除数的小数点对齐。
比较每组中的两题,你发现有什么相同?有什么不同吗?
《新编童话集》一套共4本,售价26.8元。平均每本售价多少钱?
26.8÷4
=
6.7(元)
答:平均每本售价6.7元。
练习六
爸爸给舅舅打长途电话一共花了8.4元。他们共通话12分钟,
平均每分钟付费多少钱?
8.4÷12=
0.7(元)
答:平均每分钟付费0.7元。
练习六
6.6÷4
=?
43.5÷29
=?
练习六
4.列竖式计算。
?1.65
?1.5
18.9÷27
=
1.35÷15
=?
18
9
27
0.7
0
15
1
35
0.09
0
练习六
0.7
0.09
1.35
18.9
37.5÷6=
28.6÷11
=?
练习六
6.25
2.6
20.4÷24=
3.64÷52
=?
练习六
0.85
0.07
练习六
在两栖动物中,非洲蛙是跳远冠军。一直非洲蛙曾创造了连续3次共跳跃7.74m的记录。这只非洲蛙平均一次跳多远?
7.74÷3
=
2.58(m)
答:这只非洲蛙平均一次跳2.58米。
练习六
6.下面的计算对吗?如果不对,错在哪里?
24÷15=1
6
1.26÷18=?
24
15
?
90
?
90
?
?
0
15
1
6
.
0
.
.
1.26
1.26
?
?
?0
18
0.07
0.07
0.7
0.7
15.6÷12
=1.3
12
1
.
3
12
3
6
3
6
0
验算:
1.3
×1
2
2
6
1
3
15
6
.
328÷16
=20.5
0
2
0
5
.
32
8
8
0
0
16
0
.
验算:
20.5
×
1
6
123
0
205
328
0
.
练习六
\
7.计算下面各题,并用乘法验算。
15.6÷12
?
?
?
?
?328÷16
?
?
?
?
?
?
?1.35÷27
?
?
?
?
?0.646÷19
15.6
328
7.计算下面各题,并用乘法验算。
15.6÷12
?
?
?
?
?328÷16
?
?
?
?
?
?
?1.35÷27
?
?
?
?
?0.646÷19
1.35÷27
=0.05
27
0
0
0
0
1
35
5
.
验算:
27
×0.05
1
35
.
0.646÷19
=0.034
57
76
76
0
0
3
4
.
验算:
0.034
×19
306
34
646
0.
练习六
1.35
0.646
19
8.从1997年初到2002年初,北京市5年共发放了节水龙头319.46万只。平均每年发放多少万只?
319.46÷5
=
63.892(万只)
答:平均每年发放63.892万只。
练习六
9.下面各题的商,那些是小于1的?在括号里画“√”。
?
?
?
??
?
?
?5.04÷6?
?
?
?
?76.5÷45?
?
?
?
?45÷36?
?
?
?
?0.84÷28
??
?
(?
?
?)
?
?
(?
?
?)
?
?
(?
?
?)
?
?(?
?
?)
?
想一想,什么情况下得到的商比1小?
练习六
当被除数大于除数时,商比1大。
10、五(1)班有班费24.5元,同学们卖废品又得到16.4元。
(1)一本《少年科技》多少钱?一根跳绳多少钱?
(2)你还能提出其他数学问题并解答吗?
(1)24.2+16.4=40.6(元)
40.6÷7=
5.8(元)
40.6÷14
=
2.9(元)
答:一本《少年科技》5.8元,一根跳绳2.9元。
练习六
上山:7.2÷3
=
2.4(千米/时)
下山:7.2÷2
=
3.6(千米/时)
答:上山的平均速度是2.4千米/时,下山的平均速度是3.6千米/时。
练习六
11.双休日爸爸带小勇去登山。从山脚到山顶全程有7.2km,
他们上山用了3小时下山用了2小时。上山、下山的平均速度各是多少?
你还能提出其他数学问题并解答吗?
下山比上山每小时快多少千米?
3.6-2.4=0.8(千米)
答:下山比上山每小时快0.8千米。
11.双休日爸爸带小勇去登山。从山脚到山顶全程有7.2km,
他们上山用了3小时下山用了2小时。上山、下山的平均速度各是多少?
你还能提出其他数学问题并解答吗?
练习六
12、算一算,填一填
被除数和除数同时乘或除以相同的数(0除外),商不变。
被除数
除数
商
1.5
5
15
50
150
500
0.3
0.3
0.3
练习六
提高练习
1.森林医生。
.
0
0
6
提高练习
1、填空
十分之一
百分之一
十分之一
百分之一
2、我会判断。下面各题的商,哪些是小于1的在(
)内画“√”。
提高练习
12.4÷8?
?
?
?
?
?
?
?
?
?
?
?
?1.35÷15?
?
?
?
?
?
?
?
?
?
?
?
?
?45÷36
(?
?
?)?
?
?
?
?
?
?
?
?
?
?
?
(?
?
?)?
?
?
?
?
?
?
?
?
?
?
?
?
(?
?
?)
?
?
??
10.43÷13?
?
?
?
?
?
?
?
?
?
?
4.45÷2?
?
?
?
?
?
?
?
?
?
?
?
?
?
8.2÷9
(?
?
?)?
?
?
?
?
?
?
?
?
?
?
?
(?
?
?)?
?
?
?
?
?
?
?
?
?
?
?
?
(?
?
?)
??
整数部分大于除数,商大于1
整数部分小于除数,商小于1
霸王龙玩具每盒12个,共12.6元。平均每个多少元?
提高练习
12.6÷12=
1.05(元)
答:平均每个1.05元。
?
1.05
12.6
12
?
?
60
?
?
60
?
?
?
0
12
拓展练习
2.5×50=
(
?
?
?
?
?
?)
12.5÷5
=
(?
?
?
?
?
?
)
12.5÷25=(
?
?
?
?
?
?)
1.25÷5
=
(?
?
?
?
?
?
)
0.125÷5=(
?
?
?
?
?
?)
1250÷5=
(
?
?
?
?
?
?)
1.根据2.5×5=12.5,直接写出下列各题得数。
125
2.5
0.5
0.25
0.025
250
2、两个数的和是71.5,其中一个数的小数点如果向左移动一位就等于另外一个数了,这两个数的差是多少?
拓展练习
71.5÷11=6.5??
?
?
?
?
?
?65-6.5=58.5
3.两箱水果共重24.8千克,如果从第一箱中取出3.2千克放入第二箱,则两箱水果就同样重了。第一箱水果重(?
?
)千克,第二箱水果重(?
?
?)千克。
拓展练习
24.8÷2=12.4(千克)
12.4+3.2=15.6(千克)
12.4-3.2=9.2(千克)
4、老师带学生去春游,从学校到公园一共25km。去时用了2.5小时,回来用了1.5小时。请你算一算来回平均速度是多少?
拓展练习
25+25=50(千米)
2.5+1.5=4(时)
50÷4=1.5(千米/时)
第一台电子数字计算机的诞生
?早期的计算工具?
?机械计算机?
?机电计算机?
?电子计算机
?
手指:人们习惯于十进制计数法与此有关。
?
结绳:结之多少,随物众寡。
?
算筹:祖冲之的圆周率就是借助算筹计算出来的。
??
?
?
?
?
运筹帷幄之中,决胜千里之外。
?
算盘:从唐朝一直延续到现在,仍有人在使用。
早期的计算工具
?
1614年,英国数学家约翰.纳皮尔发明简化乘除运算的纳皮尔骨条。
?
1620年,英国数学家埃德蒙.冈特发明对数计算尺。
?
1624年,英国数学家威廉.奥垂德发明了圆形滑动计算尺。
机械计算机
?
1642年,法国科学家帕斯卡发明了齿轮式能实现加减法运算的计算器Pascaline。
?
1673年,德国数学家莱布尼茨建造了一台能进行加减乘除四则运算的机械式计算机。
机械计算机
机械计算机
手摇计算机
?
1820年,法国人德.考尔玛改进了莱布尼茨的设计,研制了第
?
一台实用的机械计算机,并实现了1500台的批量生产。
?
1847年,英国数学家、逻辑学家乔治.布尔发明了布尔代数,
?
逻辑学走进了数学的领域。
?
1872年,美国人弗兰克.鲍德温开始
?
建立美国的手摇计算器工业。直到
?
1960年代电子计算机的出现,手摇计算器一直是主要的计算工具。
?
1777年,英国的查尔斯·马洪发明了逻辑演示器
。
?
1822年,英国数学家巴贝奇研制成功差分机。
机械计算机
?
1833年,巴比奇设计出
?
?
?
了分析机模型,这个模
??
?
型包括了现代计算机所
??
?
具有的5个基本组成部分。
??
?
?(P
5)
差分机
?
1886年,美国统计学家霍勒瑞斯用电磁继电器代替一部分
?
机械元件,制成了第一台机电穿孔卡系统—制表机。
?
1941年,德国工程师祖斯研制成功全部采用继电器的计算
机Z-3
,这是世界上第一台完全由程序控制的机电计算机。
?
1944年,美国哈佛大学教授霍华德.艾肯设计的机电计算机Mark-Ⅰ投入运行。在哈佛
大学服役了15年。
Mark-II的研制过程中,创造
了bug一词的新用法
机电计算机
马克一号计算机
?
1937年,美国衣阿华州立学院的阿塔纳索夫教授就开始
?
进行研制电子计算机的探索。第一台电子计算机ENIAC
?
的设计者莫奇利曾经看过他的关于电子计算机设计的笔
?
记本。
?
1946年2月15日
,世界上第一台电子数字计算机在美国
?
宾夕法尼亚大学诞生。
电子计算机
电子计算机ENIAC
电子计算机
?
ENIAC
的基本情况
–
30多岁的莫奇利提出总体设计,
24岁的埃克特负责工程技术问题,
年轻的戈尔斯坦负责组织协调。
–
占地面积170平方米;用了大约18000只电子管,1500个继电器,70000只电阻,18000只电容;耗资近49万美元;重30吨。
–
运算速度为每秒5000次加法。
–
耗电量惊人,功率为150千瓦,常常因为电子管烧坏而需要停机检修。
–
存储容量小,至多只能存20个字长为l0位的十进制数。
–
与后来的存储程序型的计算机不同,它的程序是外插型的,使用很不方便。
电子计算机
除数是整数的小数除法
经历由整数除法的计算迁移到除数是整数的小数除法计算的探究过程,理解商的小数点和被除数的小数点对齐,体会转化思想。
能正确地计算小数除以整数,进一步提高运算能力。
感受小数除以整数与生活的密切联系,培养归纳、概括的能力和良好的验算习惯。
教学目标
明确商的小数点与被除数小数点对齐的道理。
明确余数末尾添“0”继续除的道理和方法;明确首位商“0”的道理。
教学重点
教学难点
笔算下面这道题
复习简单整数除法
84÷4=
21
你能说说是怎样进行竖式计算的吗?
4
12
8
4
4
0
84
整数除法的竖式是怎样计算的?
2.
除到被除数的哪一位,就在那一
位上面写_____。
3.
求出每一位商,余下的数必须比除数
___。
王鹏的爸爸计划4个月跑步224千米,平均每个月应跑多少千米?
复习旧知
1.
从被除数的______位除起,先用除
数试除被除数的前______位数,如
果它比除数小,再试除前_____位。
最高
一
两
商
小
224÷4=
56(千米)
4
2
0
2
2
4
4
0
5
6
5个十
20个十
24个一
2
2
4
王鹏坚持晨练。他平均每周应跑多少千米?
想一想:被除数是小数该怎么除呢?
主题图导入
甲商店牛奶每袋多少元?
答:甲商店牛奶每袋2.3元。
11.5÷5=
2.3(元)
5
10
1
5
1.5
不同情境版
2
3
元
角
0
11.5
乙商店牛奶每袋多少元?哪家商店的牛奶便宜?
答:乙商店牛奶每袋2.1元。乙商店的牛奶便宜。
12.6÷6=
2.1(元)
不同情境版
12
6
6
0
2
1
6
12.6
王鹏坚持晨练。他平均每周应跑多少千米?
想一想:被除数是小数该怎么除呢?
探究新知
22.4÷4=
想一想:被除数是小数该怎么除呢?
我是这样思考的:
22.4km=22400
(m)
22400÷4=5600(m)
5600m=5.6km
讲解版
22.4÷4=
5.6(km)
商的小数点要和被除数的小数点对齐。
还可以列竖式计算。你能试一试吗?
答:他平均每周应跑5.6km。
4
2
0
4
2
2
?
4
0
5
.
讲解版
24个十分之一
……
2
2
.
4
6
22.4÷4=5.6
你理解这两种方法吗?
我把新知识转化成旧知识:
22.4km=22400m
22400÷4=5600(m)
5600m=5.6km
我用竖式计算:
探究新知
4
20
24
24
0
5.6
22.4
42÷3=
算一算,比一比
14
4.2÷3=
1.4
相同点:小数除以整数与整数除以整数的计算方法相同。
不同点:小数除以整数要把商的小数点与被除数的小数点对齐。
想一想,这两道题有哪些相同点和不同点呢?
做一做
先想一想计算时应该注意什么,再计算。
9.6÷4=
2.4
25.2÷6=
4.2
做一做
34.5÷15=
2.3
先想一想计算时应该注意什么,再计算。
18.9÷6=
不同情境版
3.15(元)
18
3
6
9
6
3
0
3
0
0
答:每把笤帚3.15元。
买6把笤帚共花了18.9元。每把笤帚多少元?估一估,算一算。
1
.
这是5个0.01
还能算下去吗?
3个0.1可以看成30个0.01
3角就是30分
5
3
18.9
26÷4=
6.5(元)
答:每把笤帚6.5元。
6
5
4
24
20
2
0
0
.
买4个簸箕共花了26元。每个簸箕多少元?请接着算下去。
不同情境版
把余数2看成20个0.1,就能除下去了。
.
26
王鹏的爷爷计划16天慢跑28km,平均每天慢跑多少千米?
探究新知
28÷16=
把计划16天慢跑的28千米平均分成16份,每份就是爷爷一天应跑的千米数。
爷爷平均每天慢跑多少千米?
王鹏的爷爷计划16天慢跑28km,平均每天慢跑多少千米?
探究新知
12表示什么,接下来该怎么除呢?
添0继续除,表示120个(?
?
?)分之一。
十
28÷16=
1
7
16
16
12
.
0
……
28
.
0
王鹏的爷爷计划16天慢跑28km,平均每天慢跑多少千米?
计算除数是整数的小数除法要注意什么?
讲解版
添0继续除,表示120个(?
?
?)分之一。
十
28÷16=
1
7
16
16
12
.
0
……
11
2
8
0
8
0
添0继续除,表示80个(?
?
?)分之一。
……
百
0
120-112=8,8比16小,还是没有除尽,该怎么办呢?
5
0
1.75(km)
答:平均每天慢跑1.75km。
商的小数点要和被除数的小数点对齐。
如果有余数,要添0再除。
28
.
0
5.6÷7=
探究新知
我每周计划跑5.6km。
一周是7天,把每周计划跑的5.6km平均分成7份,每份就是他一天跑的千米数。
他平均每天要跑多少千米?
王鹏每周计划跑5.6km,平均每天要跑多少千米?
为什么要商0呢?
整数部分不够商1,用0补位。
答:平均每天要跑0.8km。
5.6÷7=
0.8(km)
7
5
6
0
0.
8
讲解版
5.6
讲解版
怎样验算呢?自己试一试。
5.6÷7=
0.8(km)
验算:
0.
8
×
5.
6
7
7
5
6
0
0.8
5.6
计算除数是整数的除法,要注意什么呢?
按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。
整数不够除,商0,点上小数点。如果有余数,要添0再除。
讲解版
王鹏坚持晨练。他平均每天要跑多少千米?
总结版
我计划每周跑步5.6千米。
计划每周跑步5.6千米,平均每天要跑多少千米?
总结版
5.6
÷7=?
_____(千米)
0.8
整数部分不够商1时,先在商的个位上写0,点上小数点后再除。
5.6
0
8
.
7
5
6
0
当除到有余数的时候,可以在余数的末尾补“0”,然后再继续除。因为小数的末尾添0或者去掉0,小数的大小不变。
1
2
60
6
0
1
2
0
0.1
5
总结版
1.8
按照整数除法的方法计算;商的小数点与被除数的小数点对齐;
整数部分不够除,商0,点上小数点。
除到有余数时,添0再除。
总结版
?
5.6
22.4
20
?
24
?
24
?
?
0
4
0.15
1.8
1
2
?
?60
?
?60
?
?
?0
12
列竖式计算
做一做
72
÷15=
25.5÷6=
4.8
4.25
0.54÷6=
0.09
86
÷
16=
5.375
0.416÷32=
0.013
14.21÷7=
2.03
7.83÷9=
0.87
6.3÷14=
0.45
1.26÷28=
0.045
42÷3=
算一算,比一比
14
4.2÷3=
1.4
84÷4=
8.4÷4=
21
2.1
91÷14=
9.1÷14=
6.5
0.65
相同点:小数除以整数与整数除以整数的计算方法相同。
不同点:小数除以整数要把商的小数点和被除数的小数点对齐。
比较每组中的两题,你发现有什么相同?有什么不同吗?
《新编童话集》一套共4本,售价26.8元。平均每本售价多少钱?
26.8÷4
=
6.7(元)
答:平均每本售价6.7元。
练习六
爸爸给舅舅打长途电话一共花了8.4元。他们共通话12分钟,
平均每分钟付费多少钱?
8.4÷12=
0.7(元)
答:平均每分钟付费0.7元。
练习六
6.6÷4
=?
43.5÷29
=?
练习六
4.列竖式计算。
?1.65
?1.5
18.9÷27
=
1.35÷15
=?
18
9
27
0.7
0
15
1
35
0.09
0
练习六
0.7
0.09
1.35
18.9
37.5÷6=
28.6÷11
=?
练习六
6.25
2.6
20.4÷24=
3.64÷52
=?
练习六
0.85
0.07
练习六
在两栖动物中,非洲蛙是跳远冠军。一直非洲蛙曾创造了连续3次共跳跃7.74m的记录。这只非洲蛙平均一次跳多远?
7.74÷3
=
2.58(m)
答:这只非洲蛙平均一次跳2.58米。
练习六
6.下面的计算对吗?如果不对,错在哪里?
24÷15=1
6
1.26÷18=?
24
15
?
90
?
90
?
?
0
15
1
6
.
0
.
.
1.26
1.26
?
?
?0
18
0.07
0.07
0.7
0.7
15.6÷12
=1.3
12
1
.
3
12
3
6
3
6
0
验算:
1.3
×1
2
2
6
1
3
15
6
.
328÷16
=20.5
0
2
0
5
.
32
8
8
0
0
16
0
.
验算:
20.5
×
1
6
123
0
205
328
0
.
练习六
\
7.计算下面各题,并用乘法验算。
15.6÷12
?
?
?
?
?328÷16
?
?
?
?
?
?
?1.35÷27
?
?
?
?
?0.646÷19
15.6
328
7.计算下面各题,并用乘法验算。
15.6÷12
?
?
?
?
?328÷16
?
?
?
?
?
?
?1.35÷27
?
?
?
?
?0.646÷19
1.35÷27
=0.05
27
0
0
0
0
1
35
5
.
验算:
27
×0.05
1
35
.
0.646÷19
=0.034
57
76
76
0
0
3
4
.
验算:
0.034
×19
306
34
646
0.
练习六
1.35
0.646
19
8.从1997年初到2002年初,北京市5年共发放了节水龙头319.46万只。平均每年发放多少万只?
319.46÷5
=
63.892(万只)
答:平均每年发放63.892万只。
练习六
9.下面各题的商,那些是小于1的?在括号里画“√”。
?
?
?
??
?
?
?5.04÷6?
?
?
?
?76.5÷45?
?
?
?
?45÷36?
?
?
?
?0.84÷28
??
?
(?
?
?)
?
?
(?
?
?)
?
?
(?
?
?)
?
?(?
?
?)
?
想一想,什么情况下得到的商比1小?
练习六
当被除数大于除数时,商比1大。
10、五(1)班有班费24.5元,同学们卖废品又得到16.4元。
(1)一本《少年科技》多少钱?一根跳绳多少钱?
(2)你还能提出其他数学问题并解答吗?
(1)24.2+16.4=40.6(元)
40.6÷7=
5.8(元)
40.6÷14
=
2.9(元)
答:一本《少年科技》5.8元,一根跳绳2.9元。
练习六
上山:7.2÷3
=
2.4(千米/时)
下山:7.2÷2
=
3.6(千米/时)
答:上山的平均速度是2.4千米/时,下山的平均速度是3.6千米/时。
练习六
11.双休日爸爸带小勇去登山。从山脚到山顶全程有7.2km,
他们上山用了3小时下山用了2小时。上山、下山的平均速度各是多少?
你还能提出其他数学问题并解答吗?
下山比上山每小时快多少千米?
3.6-2.4=0.8(千米)
答:下山比上山每小时快0.8千米。
11.双休日爸爸带小勇去登山。从山脚到山顶全程有7.2km,
他们上山用了3小时下山用了2小时。上山、下山的平均速度各是多少?
你还能提出其他数学问题并解答吗?
练习六
12、算一算,填一填
被除数和除数同时乘或除以相同的数(0除外),商不变。
被除数
除数
商
1.5
5
15
50
150
500
0.3
0.3
0.3
练习六
提高练习
1.森林医生。
.
0
0
6
提高练习
1、填空
十分之一
百分之一
十分之一
百分之一
2、我会判断。下面各题的商,哪些是小于1的在(
)内画“√”。
提高练习
12.4÷8?
?
?
?
?
?
?
?
?
?
?
?
?1.35÷15?
?
?
?
?
?
?
?
?
?
?
?
?
?45÷36
(?
?
?)?
?
?
?
?
?
?
?
?
?
?
?
(?
?
?)?
?
?
?
?
?
?
?
?
?
?
?
?
(?
?
?)
?
?
??
10.43÷13?
?
?
?
?
?
?
?
?
?
?
4.45÷2?
?
?
?
?
?
?
?
?
?
?
?
?
?
8.2÷9
(?
?
?)?
?
?
?
?
?
?
?
?
?
?
?
(?
?
?)?
?
?
?
?
?
?
?
?
?
?
?
?
(?
?
?)
??
整数部分大于除数,商大于1
整数部分小于除数,商小于1
霸王龙玩具每盒12个,共12.6元。平均每个多少元?
提高练习
12.6÷12=
1.05(元)
答:平均每个1.05元。
?
1.05
12.6
12
?
?
60
?
?
60
?
?
?
0
12
拓展练习
2.5×50=
(
?
?
?
?
?
?)
12.5÷5
=
(?
?
?
?
?
?
)
12.5÷25=(
?
?
?
?
?
?)
1.25÷5
=
(?
?
?
?
?
?
)
0.125÷5=(
?
?
?
?
?
?)
1250÷5=
(
?
?
?
?
?
?)
1.根据2.5×5=12.5,直接写出下列各题得数。
125
2.5
0.5
0.25
0.025
250
2、两个数的和是71.5,其中一个数的小数点如果向左移动一位就等于另外一个数了,这两个数的差是多少?
拓展练习
71.5÷11=6.5??
?
?
?
?
?
?65-6.5=58.5
3.两箱水果共重24.8千克,如果从第一箱中取出3.2千克放入第二箱,则两箱水果就同样重了。第一箱水果重(?
?
)千克,第二箱水果重(?
?
?)千克。
拓展练习
24.8÷2=12.4(千克)
12.4+3.2=15.6(千克)
12.4-3.2=9.2(千克)
4、老师带学生去春游,从学校到公园一共25km。去时用了2.5小时,回来用了1.5小时。请你算一算来回平均速度是多少?
拓展练习
25+25=50(千米)
2.5+1.5=4(时)
50÷4=1.5(千米/时)
第一台电子数字计算机的诞生
?早期的计算工具?
?机械计算机?
?机电计算机?
?电子计算机
?
手指:人们习惯于十进制计数法与此有关。
?
结绳:结之多少,随物众寡。
?
算筹:祖冲之的圆周率就是借助算筹计算出来的。
??
?
?
?
?
运筹帷幄之中,决胜千里之外。
?
算盘:从唐朝一直延续到现在,仍有人在使用。
早期的计算工具
?
1614年,英国数学家约翰.纳皮尔发明简化乘除运算的纳皮尔骨条。
?
1620年,英国数学家埃德蒙.冈特发明对数计算尺。
?
1624年,英国数学家威廉.奥垂德发明了圆形滑动计算尺。
机械计算机
?
1642年,法国科学家帕斯卡发明了齿轮式能实现加减法运算的计算器Pascaline。
?
1673年,德国数学家莱布尼茨建造了一台能进行加减乘除四则运算的机械式计算机。
机械计算机
机械计算机
手摇计算机
?
1820年,法国人德.考尔玛改进了莱布尼茨的设计,研制了第
?
一台实用的机械计算机,并实现了1500台的批量生产。
?
1847年,英国数学家、逻辑学家乔治.布尔发明了布尔代数,
?
逻辑学走进了数学的领域。
?
1872年,美国人弗兰克.鲍德温开始
?
建立美国的手摇计算器工业。直到
?
1960年代电子计算机的出现,手摇计算器一直是主要的计算工具。
?
1777年,英国的查尔斯·马洪发明了逻辑演示器
。
?
1822年,英国数学家巴贝奇研制成功差分机。
机械计算机
?
1833年,巴比奇设计出
?
?
?
了分析机模型,这个模
??
?
型包括了现代计算机所
??
?
具有的5个基本组成部分。
??
?
?(P
5)
差分机
?
1886年,美国统计学家霍勒瑞斯用电磁继电器代替一部分
?
机械元件,制成了第一台机电穿孔卡系统—制表机。
?
1941年,德国工程师祖斯研制成功全部采用继电器的计算
机Z-3
,这是世界上第一台完全由程序控制的机电计算机。
?
1944年,美国哈佛大学教授霍华德.艾肯设计的机电计算机Mark-Ⅰ投入运行。在哈佛
大学服役了15年。
Mark-II的研制过程中,创造
了bug一词的新用法
机电计算机
马克一号计算机
?
1937年,美国衣阿华州立学院的阿塔纳索夫教授就开始
?
进行研制电子计算机的探索。第一台电子计算机ENIAC
?
的设计者莫奇利曾经看过他的关于电子计算机设计的笔
?
记本。
?
1946年2月15日
,世界上第一台电子数字计算机在美国
?
宾夕法尼亚大学诞生。
电子计算机
电子计算机ENIAC
电子计算机
?
ENIAC
的基本情况
–
30多岁的莫奇利提出总体设计,
24岁的埃克特负责工程技术问题,
年轻的戈尔斯坦负责组织协调。
–
占地面积170平方米;用了大约18000只电子管,1500个继电器,70000只电阻,18000只电容;耗资近49万美元;重30吨。
–
运算速度为每秒5000次加法。
–
耗电量惊人,功率为150千瓦,常常因为电子管烧坏而需要停机检修。
–
存储容量小,至多只能存20个字长为l0位的十进制数。
–
与后来的存储程序型的计算机不同,它的程序是外插型的,使用很不方便。
电子计算机
