五年级下册数学课件-暑假培优 6 较复杂的列举 人教版(22页PPT)
文档属性
| 名称 | 五年级下册数学课件-暑假培优 6 较复杂的列举 人教版(22页PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 11:26:05 | ||
图片预览







文档简介
(共22张PPT)
抢
答
游
戏
1、中国的四大名著是指?
2、唐僧有几个徒弟?
4个
抢
答
游
戏
3、世界有几大洲?几大洋?
七大洲
四大洋
抢
答
游
戏
4、TFboys
+
快乐家族
=
?个人
8
个
人
6
较复杂的列举
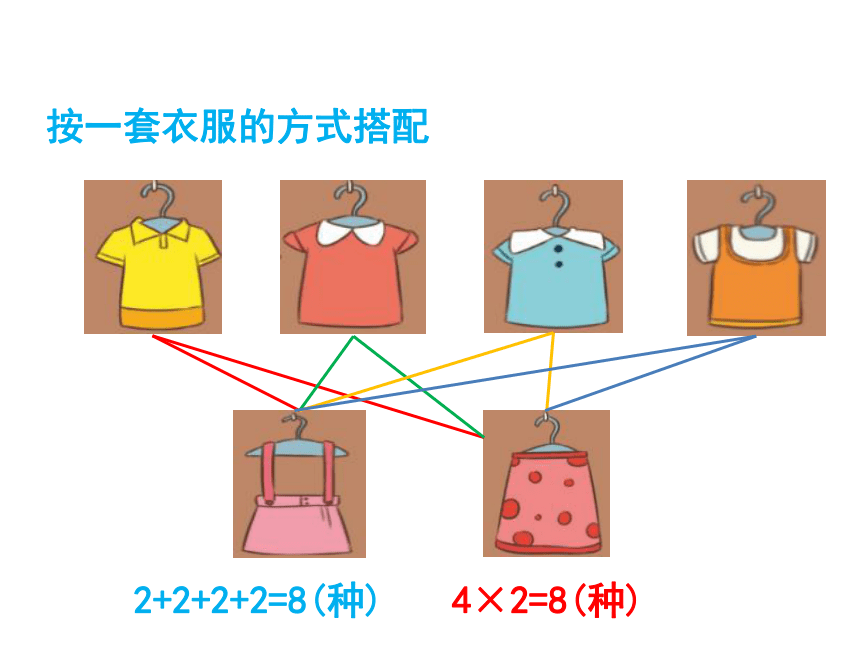
按一套衣服的方式搭配
2+2+2+2=8(种)
4×2=8(种)
例1:小孟有3件不同的上衣,4条不同的裙子,她在选择一套衣裙时共有多少种不同的搭配方法?
自己动手画一画,
连一连吧!
例1:小孟有3件不同的上衣,4条不同的裙子,她在选择一套衣裙时共有多少种不同的搭配方法?
3×4=12(种)
答:共有12种不同的搭配方法。
小孟选择一套衣裙需要分成两步:第一步选择上衣,有3种不同的选法;第二步选择裙子,有4种不同的选法。所以,完成一套衣裙的搭配一共有3×4种方法。
小
结
乘法原理:一般地,如果完成一件事需要m个步骤,其中,做第一步有a1种不同的方法,做第二步有a2种不同的方法……做第m步有am种不同的方法,那么,完成这件事一共有
N=a1×a2×…×am种不同的方法。
例2:下图中,从甲地到乙地有2条路,从乙地到丙地有3条路,从丙地至丁地也有3条路。小明从甲地到丁地去,一共有多少种不同的走法?
小明怎样才能从甲地到达丁地呢?
例2:下图中,从甲地到乙地有2条路,从乙地到丙地有3条路,从丙地至丁地也有3条路。小明从甲地到丁地去,一共有多少种不同的走法?
从甲到丁需要经过乙和丙!
从甲到丁需要分成几步完成?
例2:下图中,从甲地到乙地有2条路,从乙地到丙地有3条路,从丙地至丁地也有3条路。小明从甲地到丁地去,一共有多少种不同的走法?
分三步完成
2×3×3=18(种)
答:一共有18种不同的走法。
例3:用红、绿、黄三种颜色的油漆去涂下面的方框。每个方框涂一种颜色,且三个方框涂的颜色互不相同,共有多少种不同的涂法?
看每个方框各有几种涂法
例3:用红、绿、黄三种颜色的油漆去涂下面的方框。每个方框涂一种颜色,且三个方框涂的颜色互不相同,共有多少种不同的涂法?
有3种填法
有2种填法
有1种填法
3×2×1=6(种)
答:一共有6种不同的涂法。
例4:用2、0、7、6这四个数字,可以组成多少个没有重复数字的四位数?从大到小排列,6207是第几个?
首先确定组成的数有几个数位,再看每个数位各有几种选择方式。
例4:用2、0、7、6这四个数字,可以组成多少个没有重复数字的四位数?从大到小排列,6207是第几个?
有3种填法
有3种填法
有2种填法
3×3×2×1=18(个)
有1种填法
有0怎么办?
最高位可以是0吗?
例4:用2、0、7、6这四个数字,可以组成多少个没有重复数字的四位数?从大到小排列,6207是第几个?
从大到小排列,依次是:
7620
7602
7260
7206
7062
7026
6720
6702
6270
6207
……
第10个
答:可以组成18个没有重复数字的四位数,
从大到小排列,6207是第10个。
例5:有一群人,若规定每两个人都握手一次且只握手一次,求他们共握手多少次?假设这群人有:①两个人;②三个人;③四个人。
①两个人
1
次
例5:有一群人,若规定每两个人都握手一次且只握手一次,求他们共握手多少次?假设这群人有:①两个人;②三个人;③四个人。
②三个人
2+1=3(次)
例5:有一群人,若规定每两个人都握手一次且只握手一次,求他们共握手多少次?假设这群人有:①两个人;②三个人;③四个人。
③四个人
3+2+1=6(次)
例5:有一群人,若规定每两个人都握手一次且只握手一次,求他们共握手多少次?假设这群人有:①两个人;②三个人;③四个人。
像这种握手类型的题(单循环,不重复)的解法与数线段的方法是一样的哦!
乘法原理:一般地,如果完成一件事需要m个步骤,其中,做第一步有a1种不同的方法,做第二步有a2种不同的方法……做第m步有am种不同的方法,那么,完成这件事一共有
N=a1×a2×…×am种不同的方法。
抢
答
游
戏
1、中国的四大名著是指?
2、唐僧有几个徒弟?
4个
抢
答
游
戏
3、世界有几大洲?几大洋?
七大洲
四大洋
抢
答
游
戏
4、TFboys
+
快乐家族
=
?个人
8
个
人
6
较复杂的列举
按一套衣服的方式搭配
2+2+2+2=8(种)
4×2=8(种)
例1:小孟有3件不同的上衣,4条不同的裙子,她在选择一套衣裙时共有多少种不同的搭配方法?
自己动手画一画,
连一连吧!
例1:小孟有3件不同的上衣,4条不同的裙子,她在选择一套衣裙时共有多少种不同的搭配方法?
3×4=12(种)
答:共有12种不同的搭配方法。
小孟选择一套衣裙需要分成两步:第一步选择上衣,有3种不同的选法;第二步选择裙子,有4种不同的选法。所以,完成一套衣裙的搭配一共有3×4种方法。
小
结
乘法原理:一般地,如果完成一件事需要m个步骤,其中,做第一步有a1种不同的方法,做第二步有a2种不同的方法……做第m步有am种不同的方法,那么,完成这件事一共有
N=a1×a2×…×am种不同的方法。
例2:下图中,从甲地到乙地有2条路,从乙地到丙地有3条路,从丙地至丁地也有3条路。小明从甲地到丁地去,一共有多少种不同的走法?
小明怎样才能从甲地到达丁地呢?
例2:下图中,从甲地到乙地有2条路,从乙地到丙地有3条路,从丙地至丁地也有3条路。小明从甲地到丁地去,一共有多少种不同的走法?
从甲到丁需要经过乙和丙!
从甲到丁需要分成几步完成?
例2:下图中,从甲地到乙地有2条路,从乙地到丙地有3条路,从丙地至丁地也有3条路。小明从甲地到丁地去,一共有多少种不同的走法?
分三步完成
2×3×3=18(种)
答:一共有18种不同的走法。
例3:用红、绿、黄三种颜色的油漆去涂下面的方框。每个方框涂一种颜色,且三个方框涂的颜色互不相同,共有多少种不同的涂法?
看每个方框各有几种涂法
例3:用红、绿、黄三种颜色的油漆去涂下面的方框。每个方框涂一种颜色,且三个方框涂的颜色互不相同,共有多少种不同的涂法?
有3种填法
有2种填法
有1种填法
3×2×1=6(种)
答:一共有6种不同的涂法。
例4:用2、0、7、6这四个数字,可以组成多少个没有重复数字的四位数?从大到小排列,6207是第几个?
首先确定组成的数有几个数位,再看每个数位各有几种选择方式。
例4:用2、0、7、6这四个数字,可以组成多少个没有重复数字的四位数?从大到小排列,6207是第几个?
有3种填法
有3种填法
有2种填法
3×3×2×1=18(个)
有1种填法
有0怎么办?
最高位可以是0吗?
例4:用2、0、7、6这四个数字,可以组成多少个没有重复数字的四位数?从大到小排列,6207是第几个?
从大到小排列,依次是:
7620
7602
7260
7206
7062
7026
6720
6702
6270
6207
……
第10个
答:可以组成18个没有重复数字的四位数,
从大到小排列,6207是第10个。
例5:有一群人,若规定每两个人都握手一次且只握手一次,求他们共握手多少次?假设这群人有:①两个人;②三个人;③四个人。
①两个人
1
次
例5:有一群人,若规定每两个人都握手一次且只握手一次,求他们共握手多少次?假设这群人有:①两个人;②三个人;③四个人。
②三个人
2+1=3(次)
例5:有一群人,若规定每两个人都握手一次且只握手一次,求他们共握手多少次?假设这群人有:①两个人;②三个人;③四个人。
③四个人
3+2+1=6(次)
例5:有一群人,若规定每两个人都握手一次且只握手一次,求他们共握手多少次?假设这群人有:①两个人;②三个人;③四个人。
像这种握手类型的题(单循环,不重复)的解法与数线段的方法是一样的哦!
乘法原理:一般地,如果完成一件事需要m个步骤,其中,做第一步有a1种不同的方法,做第二步有a2种不同的方法……做第m步有am种不同的方法,那么,完成这件事一共有
N=a1×a2×…×am种不同的方法。
