四年级上册数学课件 角的度量人教版51张ppt
文档属性
| 名称 | 四年级上册数学课件 角的度量人教版51张ppt |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 06:23:11 | ||
图片预览




文档简介
角的度量
认识量角器,知道角的度量单位,掌握用量角器度量角的步骤和方法,初步渗透符号化思想。?
经历分析与归纳的过程,培养分析问题和解决问题的能力。
借助量角的大小进一步明确角的大小与边的长短无关,与两边叉开的大小有关。
教学目标
教学重点
认识量角器,会用量角器量角。
教学难点
学会应用量角器或三角板。
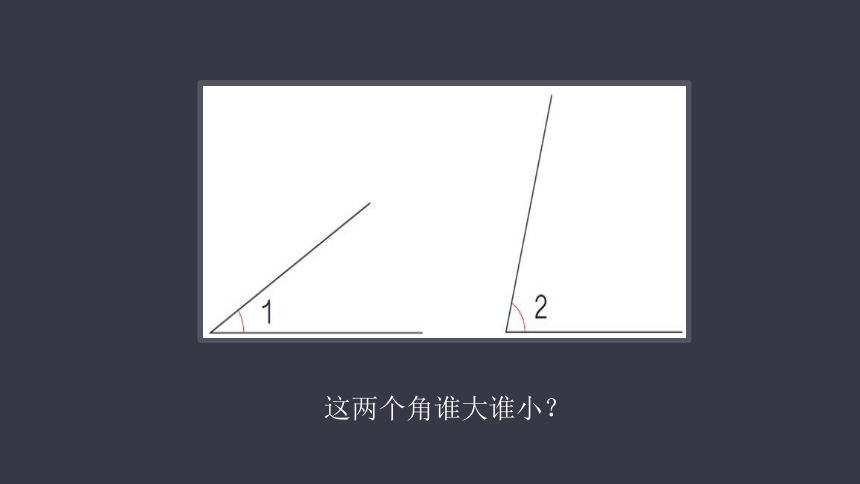
这两个角谁大谁小?
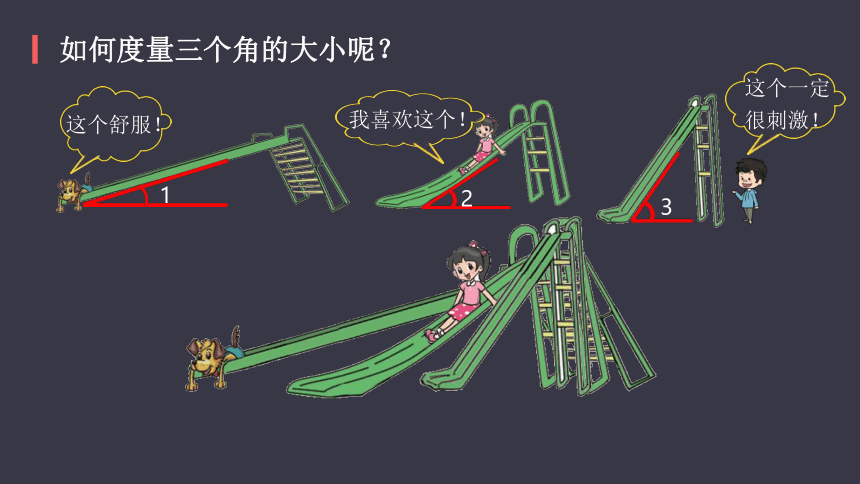
如何度量三个角的大小呢?
1
2
3
这个舒服!
我喜欢这个!
这个一定很刺激!
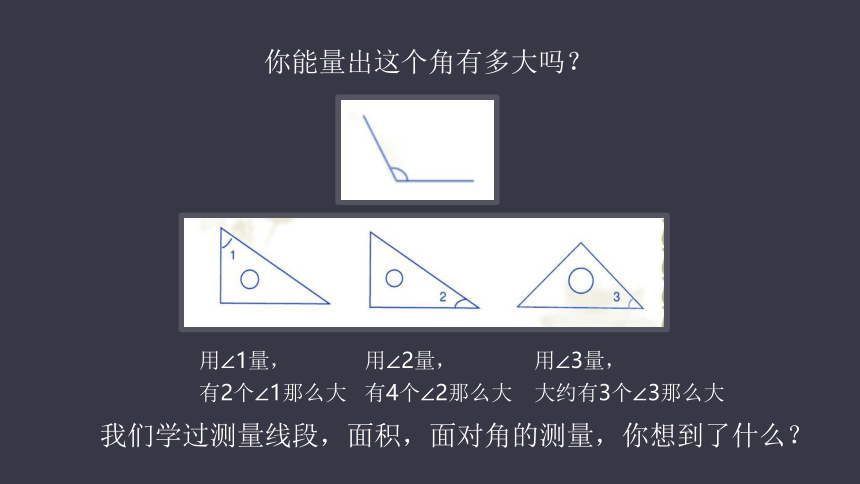
你能量出这个角有多大吗?
用∠1量,
有2个∠1那么大
用∠2量,
有4个∠2那么大
用∠3量,
大约有3个∠3那么大
我们学过测量线段,面积,面对角的测量,你想到了什么?
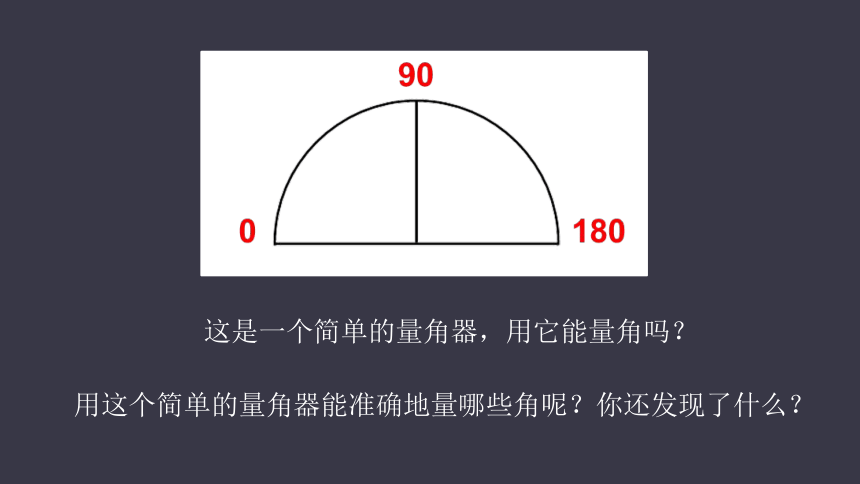
这是一个简单的量角器,用它能量角吗?
用这个简单的量角器能准确地量哪些角呢?你还发现了什么???
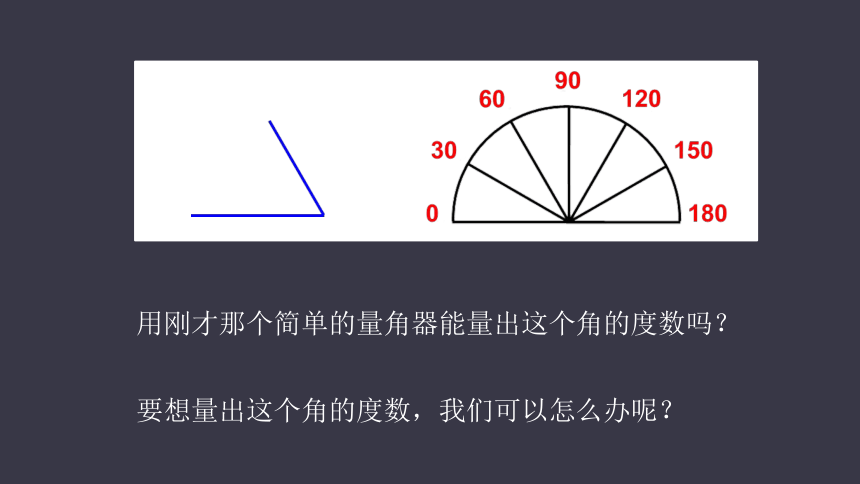
用刚才那个简单的量角器能量出这个角的度数吗?
要想量出这个角的度数,我们可以怎么办呢?
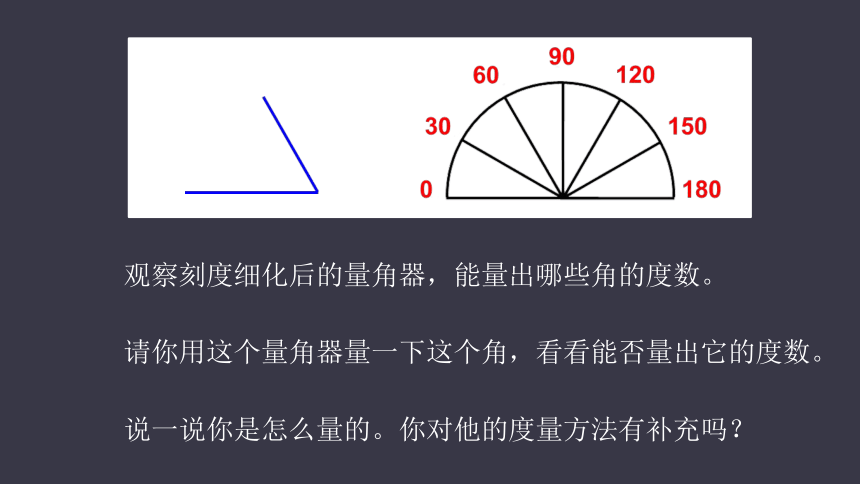
观察刻度细化后的量角器,能量出哪些角的度数。??
请你用这个量角器量一下这个角,看看能否量出它的度数。
说一说你是怎么量的。你对他的度量方法有补充吗?
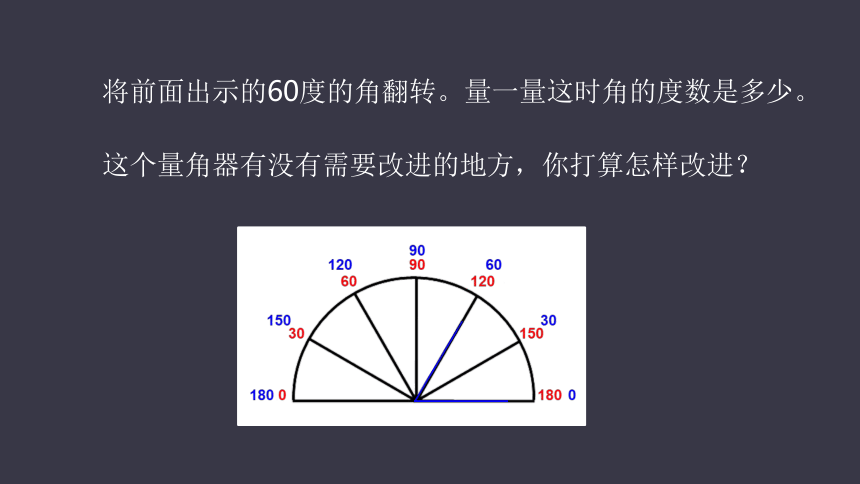
将前面出示的60度的角翻转。量一量这时角的度数是多少。
这个量角器有没有需要改进的地方,你打算怎样改进??
这个量角器能量出哪些角的度数?
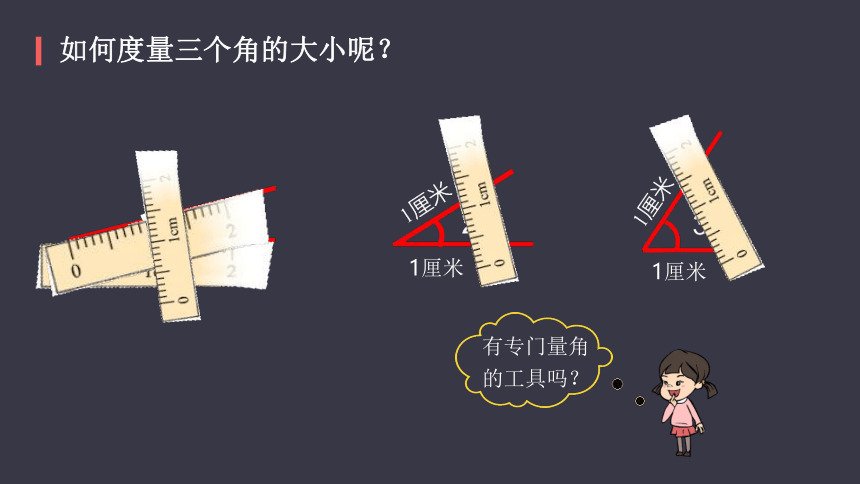
如何度量三个角的大小呢?
1厘米
1厘米
有专门量角的工具吗?
如果折的角再小
一点,会更准确。
想一想,认一认
想一想,认一认
比一比,下面两个角谁大?
仔细观察量角器上有什么?
角的计量单位是“度”, 用符号“ °”表示。把半圆分成180等份, 每一份所对的角的大小是1度, 记作1°。
试一试:读出下面角的度数。?
1. 把量角器放在角的上面,使量角器的中心点和角的顶点重合。
2. 零度刻度线和角的一条边重合。
3. 角的另一条边所对的量角器上的刻度,就是这个角的度数。
点对点,线对边,读数要看另一边;0在内读内,0在外读外。
测量角的歌诀:? ??
再看刻度没问题。
一边看零在哪里,
内圈外圈要分清。
一条边来对准零,
顶点放在中心上。
量角要从顶点起,
比一比,下面两个角谁大?
量角器的中心与角的顶点重合,0°刻度线与角的一条边重合。
1. 请你量出刚才这个∠1的度数。然后再和同学们说一说你是怎样用量角器量∠1的。
2. 谁来说一说∠1多少度?你是怎么量的?
3. 有什么需要注意的吗?
4. 问题:现在请你量一量∠2,看看∠2多少度。
1
观察量角器,认一认,说一说
中心点
零刻度线
估一估,并量出下面两个角的度数,说说你是怎么量的。
∠1=_____ °
∠2=_____ °
70
110
做一做
50°
55°
两个角的大小相等,角的大小与边的长短没有关系。
做一做
做一做
练习七
2、先估计三角尺上各个角的度数,再量一量。
45°
45°
30°
60°
1
2
3
1
2
3
∠1=_____
∠2=_____
∠3=_____
∠1=_____
∠2=_____
∠3=_____
练习七
3、量一量下面的角各是多少度。
55°
110°
36°
108°
55°
练习七
4、量出下面各角的度数。你能发现什么?
∠1=_____
∠2=_____
∠3=_____
∠4=_____
155°
25°
155°
25°
练习七
45°
150°
60°
1.把圆平均分成360份,将其中一份所对的角作为度量角的
单位,它的大小就是(? ? ?)度,记作(? ? ?)。? ? ?
提高练习
2.用一个放大镜看103°角,这个角是(? ? ? ? ? )度。
1
1°
103?
提高练习
2.用量角器量一量三角尺上每个角各是多少度。
提高练习
3.写出下面各角的度数。
45°
90°
120°
拓展练习
1.连接AB、BC、AC,形成三个角,用量角器量一量各角分别是多少度,再算一算它们的和是多少度?
A
B
C
2.用先估一估下图中各角的度数,然后量一量,你估得准吗?
拓展练习
拓展练习
3.量一量生活中的角。
线段AB 和BC 哪个长?
其实一样长
这个是圆吗??
【解析】两种解读都能看到。但是,在任何时候,你都只能看见面孔或只能看见花瓶。如果继续看,图形会自己调换以使你在面孔和花瓶之间只能选择看到一个。作者:心理学家爱德加·鲁宾,其灵感来源于一张19世纪的智力玩具卡片。
图中两只眼睛看起来排错了吗?那就请用直尺检查一下吧!
凯尼泽三角形
你能看见三角形吗?
虽然它们没有边缘和轮廓。?
你能看出这个球体吗?尽管没有边缘和阴影限定它。
? ? ? ? 平行的黑线完全是笔直而平行的,放射线会歪曲人对线条和形状的感知,这种经典幻觉由19世纪初德国心理学家艾沃德·黑林首先发现。 此图属于“黑林错觉”。并在当时用于研究人眼对错觉的判断,到19世纪末曾试用于审判犯人。这种错觉的具体原理尚在研究中。这是由于当人观察物体时,基于经验主义或不当的参照所形成的错误的判断和感知。
认识量角器,知道角的度量单位,掌握用量角器度量角的步骤和方法,初步渗透符号化思想。?
经历分析与归纳的过程,培养分析问题和解决问题的能力。
借助量角的大小进一步明确角的大小与边的长短无关,与两边叉开的大小有关。
教学目标
教学重点
认识量角器,会用量角器量角。
教学难点
学会应用量角器或三角板。
这两个角谁大谁小?
如何度量三个角的大小呢?
1
2
3
这个舒服!
我喜欢这个!
这个一定很刺激!
你能量出这个角有多大吗?
用∠1量,
有2个∠1那么大
用∠2量,
有4个∠2那么大
用∠3量,
大约有3个∠3那么大
我们学过测量线段,面积,面对角的测量,你想到了什么?
这是一个简单的量角器,用它能量角吗?
用这个简单的量角器能准确地量哪些角呢?你还发现了什么???
用刚才那个简单的量角器能量出这个角的度数吗?
要想量出这个角的度数,我们可以怎么办呢?
观察刻度细化后的量角器,能量出哪些角的度数。??
请你用这个量角器量一下这个角,看看能否量出它的度数。
说一说你是怎么量的。你对他的度量方法有补充吗?
将前面出示的60度的角翻转。量一量这时角的度数是多少。
这个量角器有没有需要改进的地方,你打算怎样改进??
这个量角器能量出哪些角的度数?
如何度量三个角的大小呢?
1厘米
1厘米
有专门量角的工具吗?
如果折的角再小
一点,会更准确。
想一想,认一认
想一想,认一认
比一比,下面两个角谁大?
仔细观察量角器上有什么?
角的计量单位是“度”, 用符号“ °”表示。把半圆分成180等份, 每一份所对的角的大小是1度, 记作1°。
试一试:读出下面角的度数。?
1. 把量角器放在角的上面,使量角器的中心点和角的顶点重合。
2. 零度刻度线和角的一条边重合。
3. 角的另一条边所对的量角器上的刻度,就是这个角的度数。
点对点,线对边,读数要看另一边;0在内读内,0在外读外。
测量角的歌诀:? ??
再看刻度没问题。
一边看零在哪里,
内圈外圈要分清。
一条边来对准零,
顶点放在中心上。
量角要从顶点起,
比一比,下面两个角谁大?
量角器的中心与角的顶点重合,0°刻度线与角的一条边重合。
1. 请你量出刚才这个∠1的度数。然后再和同学们说一说你是怎样用量角器量∠1的。
2. 谁来说一说∠1多少度?你是怎么量的?
3. 有什么需要注意的吗?
4. 问题:现在请你量一量∠2,看看∠2多少度。
1
观察量角器,认一认,说一说
中心点
零刻度线
估一估,并量出下面两个角的度数,说说你是怎么量的。
∠1=_____ °
∠2=_____ °
70
110
做一做
50°
55°
两个角的大小相等,角的大小与边的长短没有关系。
做一做
做一做
练习七
2、先估计三角尺上各个角的度数,再量一量。
45°
45°
30°
60°
1
2
3
1
2
3
∠1=_____
∠2=_____
∠3=_____
∠1=_____
∠2=_____
∠3=_____
练习七
3、量一量下面的角各是多少度。
55°
110°
36°
108°
55°
练习七
4、量出下面各角的度数。你能发现什么?
∠1=_____
∠2=_____
∠3=_____
∠4=_____
155°
25°
155°
25°
练习七
45°
150°
60°
1.把圆平均分成360份,将其中一份所对的角作为度量角的
单位,它的大小就是(? ? ?)度,记作(? ? ?)。? ? ?
提高练习
2.用一个放大镜看103°角,这个角是(? ? ? ? ? )度。
1
1°
103?
提高练习
2.用量角器量一量三角尺上每个角各是多少度。
提高练习
3.写出下面各角的度数。
45°
90°
120°
拓展练习
1.连接AB、BC、AC,形成三个角,用量角器量一量各角分别是多少度,再算一算它们的和是多少度?
A
B
C
2.用先估一估下图中各角的度数,然后量一量,你估得准吗?
拓展练习
拓展练习
3.量一量生活中的角。
线段AB 和BC 哪个长?
其实一样长
这个是圆吗??
【解析】两种解读都能看到。但是,在任何时候,你都只能看见面孔或只能看见花瓶。如果继续看,图形会自己调换以使你在面孔和花瓶之间只能选择看到一个。作者:心理学家爱德加·鲁宾,其灵感来源于一张19世纪的智力玩具卡片。
图中两只眼睛看起来排错了吗?那就请用直尺检查一下吧!
凯尼泽三角形
你能看见三角形吗?
虽然它们没有边缘和轮廓。?
你能看出这个球体吗?尽管没有边缘和阴影限定它。
? ? ? ? 平行的黑线完全是笔直而平行的,放射线会歪曲人对线条和形状的感知,这种经典幻觉由19世纪初德国心理学家艾沃德·黑林首先发现。 此图属于“黑林错觉”。并在当时用于研究人眼对错觉的判断,到19世纪末曾试用于审判犯人。这种错觉的具体原理尚在研究中。这是由于当人观察物体时,基于经验主义或不当的参照所形成的错误的判断和感知。
