1.3 探索三角形全等的条件 课件(共28张PPT)
文档属性
| 名称 | 1.3 探索三角形全等的条件 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 08:33:02 | ||
图片预览




文档简介
第一章 三角形
3 探索三角形全等的条件
知识点一 用“边边边(SSS)”判定两个三角形全等
内容
应用格式
图形表示
边边边(SSS)
三边分别相等的两个三角形全等,简写为“边边边”或“SSS”
在△ABC和△A’B’C’中,因为AB=A’B’,BC=B’C’,AC=A’C’,所以△ABC≌△A’B’C’
知识
详解
利用“边边边”判定三角形全等时,当所给的相等的线段不是要判定的三角形的边时,往往利用等式的性质,转化为两个三角形的边
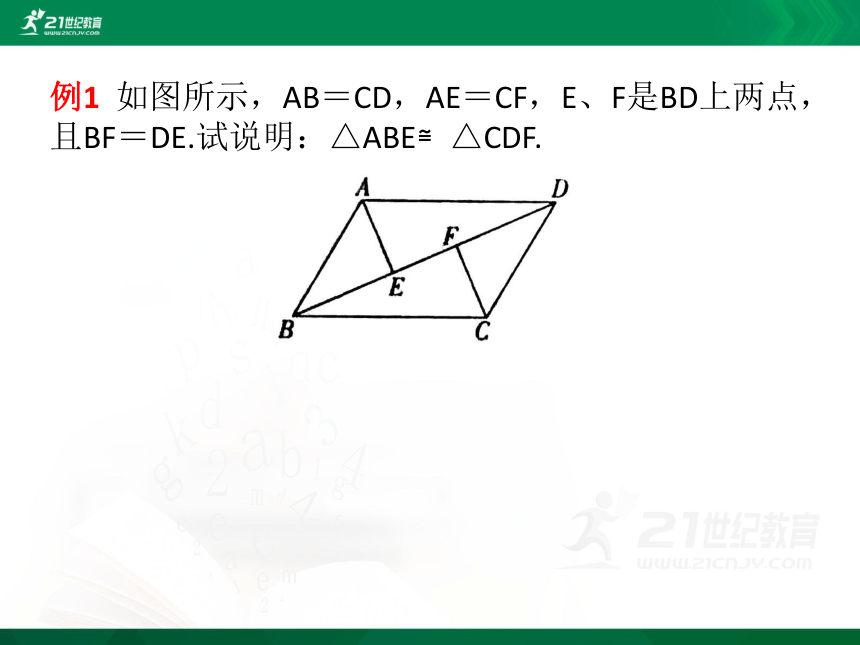
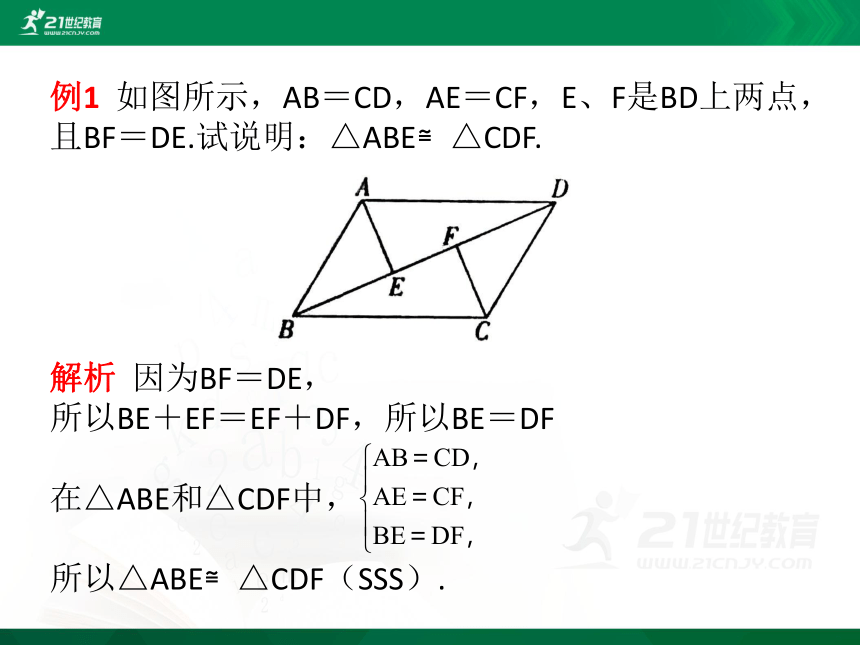
例1 如图所示,AB=CD,AE=CF,E、F是BD上两点,且BF=DE.试说明:△ABE≌△CDF.
例1 如图所示,AB=CD,AE=CF,E、F是BD上两点,且BF=DE.试说明:△ABE≌△CDF.
解析 因为BF=DE,
所以BE+EF=EF+DF,所以BE=DF
在△ABE和△CDF中,
所以△ABE≌△CDF(SSS).
知识点二 三角形的稳定性
只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,三角形的这个性质叫做三的稳定性这种性质表现为判定三角形全等的条件“SSS”,与角无关.
知识点二 三角形的稳定性
只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,三角形的这个性质叫做三的稳定性这种性质表现为判定三角形全等的条件“SSS”,与角无关.
知识详解
(1)要看图形是不是具有稳定性,关键在于它的结构是不是三角形结构.
(2)四边形具有不稳定性.
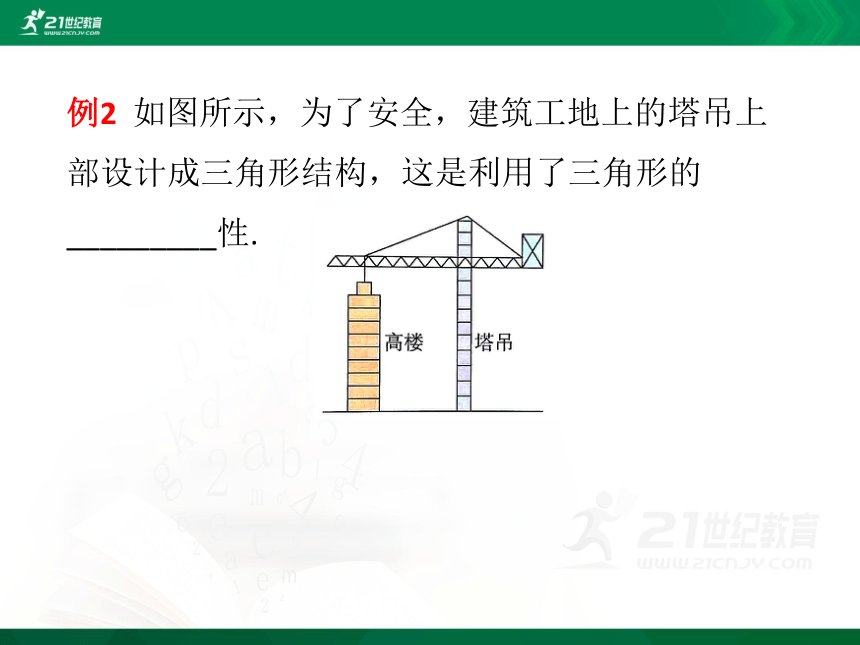
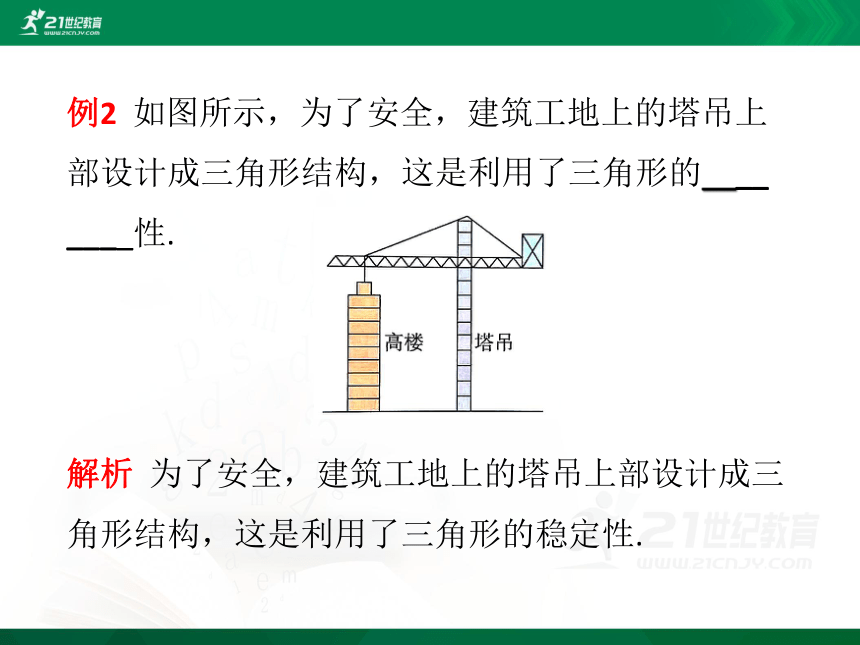
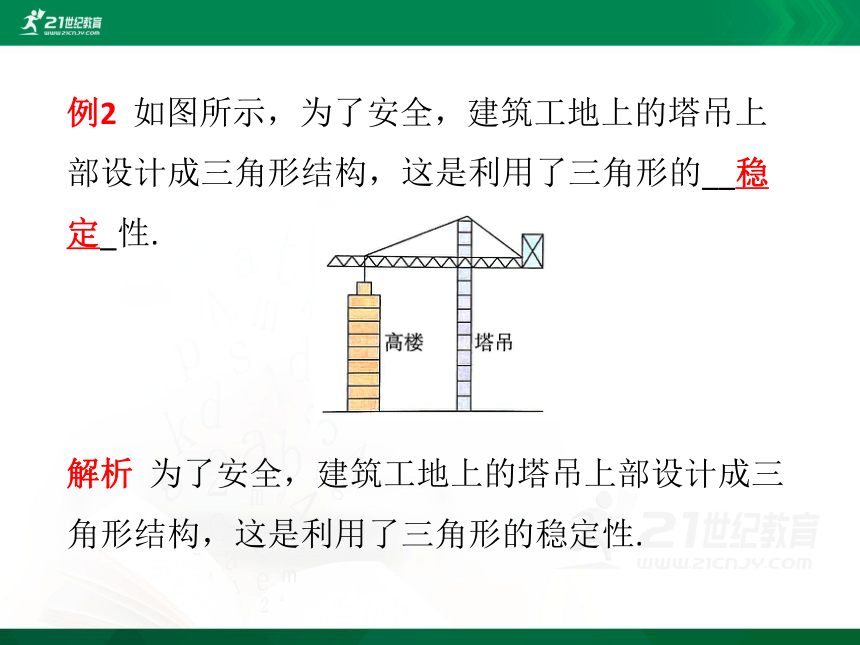
例2 如图所示,为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的_________性.
例2 如图所示,为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的____
____性.
解析 为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的稳定性.
例2 如图所示,为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的__稳定_性.
解析 为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的稳定性.
知识点三 用“角边角(ASA)”判定两个三角形全等
内容
应用格式
图形表示
角边角(ASA)
两角和它们的夹边分别相等的两个三角形全等,简写为“角边角”或“ASA”
在△ABC和△A’B’C’中,因为∠B=∠B’,BC=B’C’,∠C=∠C’,所以△ABC≌△A’B’C’
知识
详解
(1)用“ASA”判定两个三角形全等时,一定要说明这两个三角形有两个角相等以及这两个角的夹边相等.
(2)在书写两个三角形全等的条件“ASA”时,夹边相等写在中间,以突出边的位置.
例2 已知,如图所示,AB=AD,∠B=∠D,∠1=∠2.试说明:△ADE≌△ABC.
例2 已知,如图所示,AB=AD,∠B=∠D,∠1=∠2.试说明:△ADE≌△ABC.
解析 因为∠I=∠2,
所以∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC,
在△ABC和△ADE中,
所以△ABC≌△ADE(ASA).
知识点四 用“角角边(AAS)"判定两个三角形全等
内容
应用格式
图形表示
角角边(AAS)
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写为“角角边”或“AAS”
在△ABC和△A’B’C’中,因为∠A=∠A’,∠B=∠B’,BC=B’C’,所以△ABC≌△A’B’C’
知识
详解
(1)用“AAS”来判定两个三角形全等时,要注意边是其中一组等角的对边.(2)“AAS”与“ASA”的联系与区别:根据三角形的内角和定理可知,“AAS”可由“ASA”推导得出,将两者结合起来可得出:两个三角形,如果具备两个角和一条边对应相等,那么可判定这两个三角形全等,其中“对应”必不可少假如一个三角形中相等的边是两角的夹边,而另一个三角形中相等的边是其中一个角的对边,则这两个三角形不一定全等.
例4 如图所示,已知在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.试说明:AD=BC.
例4 如图所示,已知在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.试说明:AD=BC.
解析 因为AD∥BC,所以∠A=∠C,
因为AE=CF,所以AE+EF=CF+EF,即AF=CE,
因为在△ADF和△CBE中,
所以△ADF≌△CBE(AAS),所以AD=BC.
知识点五 用“边角边(SAS)”判定两个三角形全等
内容
应用格式
图形表示
边角边(SAS)
两边及其夹角分别相等的两个三角形全等,简写为“边角边”或“SAS”
在△ABC和△A’B’C’中,因为AB=A’B’,∠B=∠B’,BC=B’C’,所以△ABC≌△A’B’C’
知识
详解
(1)用“SAS”判定两个三角形全等时,对应相等的角必须是两条边的夹角,而不是其中一边的对角书写时,要按照边角边的顺序来写.
(2)当角是一组相等边的对角,即两边和其中
一边的对角分别相等时,两个三角形不一定全
等如图所示,在△ABC和△ABD中,AB=AB,
AC=AD,∠B=∠B(∠B是AC、AD边的对角),
显然△ABC和△ABD不全等.
例5 如图所示,AE=DB,BC=EF,BC∥EF,试说明:
△ABC≌△DEF.
例5 如图所示,AE=DB,BC=EF,BC∥EF,试说明:
△ABC≌△DEF.
解析 因为BC∥EF,所以∠ABC=∠DEF,
因为AE=BD,所以AE+BE=BD+BE,所以AB=DE,
在△ABC和△DEF中,
所以△ABC≌△DEF(SAS).
知识点六 三角形全等条件的灵活选用
判定两个三角形全等时,如果给出的条件不全面,那么需要根据已知条件结合相应的定理进行分析,先推导出所缺的条件,再证明.
具体思路如下:
(1)已知两边
思路一(找第三边)
思路二(找夹角)
AB=DE, BC=EF
首先推导AC=DF,然后应用“SSS”判定全等
首先推导∠B=∠E,然后应用“SAS”判定全等
(2)已知两角
思路一(找夹边)
思路二(找角的对边)
∠A=∠D,∠B=∠E
首先推导AB=DE,然后应用“ASA”判定全等
首先推导AC=DF或BC=EF,然后应用“AAS”判定全等
(3)已知一边一角
思路一(找夹角另一边)
思路二(找夹边另一角)
思路三(找边的对角)
①边为角的邻边:AB=DE,∠B=∠E
首先推导BC=EF,然后应用“SAS"判定全等
首先推导∠A=∠D,然后应用“ASA”判定全等
首先推导∠C=∠F,然后应用“AAS”判定全等
②边为角的对边:AC=DF,∠B=∠E
思路(找边的邻角对应相等)
首先推导∠A=∠D或∠C=∠F,然后应用“AAS”判定全等
例6 如图所示,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“SAS”需添加条件_________________;
(2)根据“ASA”需添加条件_________________;
(3)根据“AAS”需添加条件_________________;
解析: ∵AD平分∠BAC,∴∠BAD=∠CAD,∵AD=AD,
∴(1)要使△ABD≌△ACD,根据“SAS”可添加条件AB=AC.
(2)要使△ABD≌△ACD,根据“ASA”可添加条件∠BDA=∠CDA.
(3)要使△ABD≌△ACD,根据“AAS”可添加条件∠B=∠C.
解析: ∵AD平分∠BAC,∴∠BAD=∠CAD,∵AD=AD,
∴(1)要使△ABD≌△ACD,根据“SAS”可添加条件AB=AC.
(2)要使△ABD≌△ACD,根据“ASA”可添加条件∠BDA=∠CDA.
(3)要使△ABD≌△ACD,根据“AAS”可添加条件∠B=∠C.
答案
(1)AB=AC (2)∠BDA=∠CDA (3)∠B=∠C
经典例题
题型 全等三角形性质与判定的综合运用
例题 如图所示,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,BF=AC.
(1)求证:DF=DC;
(2)若BC=7,DF=3,求出AF的长度.
解析(1)因为AD⊥BC,BE⊥AC,
所以∠ADB=∠ADC=∠BEC=90°,
所以∠FBD+∠C=∠CAD+∠C=90°,
所以∠FBD=∠CAD,
在△BFD和△ACD中,
所以△BFD≌△ACD(AAS),所以DF=DC.
(2)因为DC=DF=3,所以BD=BC-DC=7-3=4,
因为△BFD≌△ACD,所以AD=BD=4,
所以AF=AD-DF=4-3=1.
解析(1)因为AD⊥BC,BE⊥AC,
所以∠ADB=∠ADC=∠BEC=90°,
所以∠FBD+∠C=∠CAD+∠C=90°,
所以∠FBD=∠CAD,
在△BFD和△ACD中,
所以△BFD≌△ACD(AAS),所以DF=DC.
(2)因为DC=DF=3,所以BD=BC-DC=7-3=4,
因为△BFD≌△ACD,所以AD=BD=4,
所以AF=AD-DF=4-3=1.
点拨 解决问题时要注意对图形本身的隐含条件的挖掘,如:对顶角、公共角、公共边等.
3 探索三角形全等的条件
知识点一 用“边边边(SSS)”判定两个三角形全等
内容
应用格式
图形表示
边边边(SSS)
三边分别相等的两个三角形全等,简写为“边边边”或“SSS”
在△ABC和△A’B’C’中,因为AB=A’B’,BC=B’C’,AC=A’C’,所以△ABC≌△A’B’C’
知识
详解
利用“边边边”判定三角形全等时,当所给的相等的线段不是要判定的三角形的边时,往往利用等式的性质,转化为两个三角形的边
例1 如图所示,AB=CD,AE=CF,E、F是BD上两点,且BF=DE.试说明:△ABE≌△CDF.
例1 如图所示,AB=CD,AE=CF,E、F是BD上两点,且BF=DE.试说明:△ABE≌△CDF.
解析 因为BF=DE,
所以BE+EF=EF+DF,所以BE=DF
在△ABE和△CDF中,
所以△ABE≌△CDF(SSS).
知识点二 三角形的稳定性
只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,三角形的这个性质叫做三的稳定性这种性质表现为判定三角形全等的条件“SSS”,与角无关.
知识点二 三角形的稳定性
只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,三角形的这个性质叫做三的稳定性这种性质表现为判定三角形全等的条件“SSS”,与角无关.
知识详解
(1)要看图形是不是具有稳定性,关键在于它的结构是不是三角形结构.
(2)四边形具有不稳定性.
例2 如图所示,为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的_________性.
例2 如图所示,为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的____
____性.
解析 为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的稳定性.
例2 如图所示,为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的__稳定_性.
解析 为了安全,建筑工地上的塔吊上部设计成三角形结构,这是利用了三角形的稳定性.
知识点三 用“角边角(ASA)”判定两个三角形全等
内容
应用格式
图形表示
角边角(ASA)
两角和它们的夹边分别相等的两个三角形全等,简写为“角边角”或“ASA”
在△ABC和△A’B’C’中,因为∠B=∠B’,BC=B’C’,∠C=∠C’,所以△ABC≌△A’B’C’
知识
详解
(1)用“ASA”判定两个三角形全等时,一定要说明这两个三角形有两个角相等以及这两个角的夹边相等.
(2)在书写两个三角形全等的条件“ASA”时,夹边相等写在中间,以突出边的位置.
例2 已知,如图所示,AB=AD,∠B=∠D,∠1=∠2.试说明:△ADE≌△ABC.
例2 已知,如图所示,AB=AD,∠B=∠D,∠1=∠2.试说明:△ADE≌△ABC.
解析 因为∠I=∠2,
所以∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC,
在△ABC和△ADE中,
所以△ABC≌△ADE(ASA).
知识点四 用“角角边(AAS)"判定两个三角形全等
内容
应用格式
图形表示
角角边(AAS)
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写为“角角边”或“AAS”
在△ABC和△A’B’C’中,因为∠A=∠A’,∠B=∠B’,BC=B’C’,所以△ABC≌△A’B’C’
知识
详解
(1)用“AAS”来判定两个三角形全等时,要注意边是其中一组等角的对边.(2)“AAS”与“ASA”的联系与区别:根据三角形的内角和定理可知,“AAS”可由“ASA”推导得出,将两者结合起来可得出:两个三角形,如果具备两个角和一条边对应相等,那么可判定这两个三角形全等,其中“对应”必不可少假如一个三角形中相等的边是两角的夹边,而另一个三角形中相等的边是其中一个角的对边,则这两个三角形不一定全等.
例4 如图所示,已知在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.试说明:AD=BC.
例4 如图所示,已知在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.试说明:AD=BC.
解析 因为AD∥BC,所以∠A=∠C,
因为AE=CF,所以AE+EF=CF+EF,即AF=CE,
因为在△ADF和△CBE中,
所以△ADF≌△CBE(AAS),所以AD=BC.
知识点五 用“边角边(SAS)”判定两个三角形全等
内容
应用格式
图形表示
边角边(SAS)
两边及其夹角分别相等的两个三角形全等,简写为“边角边”或“SAS”
在△ABC和△A’B’C’中,因为AB=A’B’,∠B=∠B’,BC=B’C’,所以△ABC≌△A’B’C’
知识
详解
(1)用“SAS”判定两个三角形全等时,对应相等的角必须是两条边的夹角,而不是其中一边的对角书写时,要按照边角边的顺序来写.
(2)当角是一组相等边的对角,即两边和其中
一边的对角分别相等时,两个三角形不一定全
等如图所示,在△ABC和△ABD中,AB=AB,
AC=AD,∠B=∠B(∠B是AC、AD边的对角),
显然△ABC和△ABD不全等.
例5 如图所示,AE=DB,BC=EF,BC∥EF,试说明:
△ABC≌△DEF.
例5 如图所示,AE=DB,BC=EF,BC∥EF,试说明:
△ABC≌△DEF.
解析 因为BC∥EF,所以∠ABC=∠DEF,
因为AE=BD,所以AE+BE=BD+BE,所以AB=DE,
在△ABC和△DEF中,
所以△ABC≌△DEF(SAS).
知识点六 三角形全等条件的灵活选用
判定两个三角形全等时,如果给出的条件不全面,那么需要根据已知条件结合相应的定理进行分析,先推导出所缺的条件,再证明.
具体思路如下:
(1)已知两边
思路一(找第三边)
思路二(找夹角)
AB=DE, BC=EF
首先推导AC=DF,然后应用“SSS”判定全等
首先推导∠B=∠E,然后应用“SAS”判定全等
(2)已知两角
思路一(找夹边)
思路二(找角的对边)
∠A=∠D,∠B=∠E
首先推导AB=DE,然后应用“ASA”判定全等
首先推导AC=DF或BC=EF,然后应用“AAS”判定全等
(3)已知一边一角
思路一(找夹角另一边)
思路二(找夹边另一角)
思路三(找边的对角)
①边为角的邻边:AB=DE,∠B=∠E
首先推导BC=EF,然后应用“SAS"判定全等
首先推导∠A=∠D,然后应用“ASA”判定全等
首先推导∠C=∠F,然后应用“AAS”判定全等
②边为角的对边:AC=DF,∠B=∠E
思路(找边的邻角对应相等)
首先推导∠A=∠D或∠C=∠F,然后应用“AAS”判定全等
例6 如图所示,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“SAS”需添加条件_________________;
(2)根据“ASA”需添加条件_________________;
(3)根据“AAS”需添加条件_________________;
解析: ∵AD平分∠BAC,∴∠BAD=∠CAD,∵AD=AD,
∴(1)要使△ABD≌△ACD,根据“SAS”可添加条件AB=AC.
(2)要使△ABD≌△ACD,根据“ASA”可添加条件∠BDA=∠CDA.
(3)要使△ABD≌△ACD,根据“AAS”可添加条件∠B=∠C.
解析: ∵AD平分∠BAC,∴∠BAD=∠CAD,∵AD=AD,
∴(1)要使△ABD≌△ACD,根据“SAS”可添加条件AB=AC.
(2)要使△ABD≌△ACD,根据“ASA”可添加条件∠BDA=∠CDA.
(3)要使△ABD≌△ACD,根据“AAS”可添加条件∠B=∠C.
答案
(1)AB=AC (2)∠BDA=∠CDA (3)∠B=∠C
经典例题
题型 全等三角形性质与判定的综合运用
例题 如图所示,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,BF=AC.
(1)求证:DF=DC;
(2)若BC=7,DF=3,求出AF的长度.
解析(1)因为AD⊥BC,BE⊥AC,
所以∠ADB=∠ADC=∠BEC=90°,
所以∠FBD+∠C=∠CAD+∠C=90°,
所以∠FBD=∠CAD,
在△BFD和△ACD中,
所以△BFD≌△ACD(AAS),所以DF=DC.
(2)因为DC=DF=3,所以BD=BC-DC=7-3=4,
因为△BFD≌△ACD,所以AD=BD=4,
所以AF=AD-DF=4-3=1.
解析(1)因为AD⊥BC,BE⊥AC,
所以∠ADB=∠ADC=∠BEC=90°,
所以∠FBD+∠C=∠CAD+∠C=90°,
所以∠FBD=∠CAD,
在△BFD和△ACD中,
所以△BFD≌△ACD(AAS),所以DF=DC.
(2)因为DC=DF=3,所以BD=BC-DC=7-3=4,
因为△BFD≌△ACD,所以AD=BD=4,
所以AF=AD-DF=4-3=1.
点拨 解决问题时要注意对图形本身的隐含条件的挖掘,如:对顶角、公共角、公共边等.
