数学:7.1《不等式的性质》课件(沪科版七年级下)
文档属性
| 名称 | 数学:7.1《不等式的性质》课件(沪科版七年级下) |  | |
| 格式 | zip | ||
| 文件大小 | 180.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-15 20:52:12 | ||
图片预览








文档简介
(共22张PPT)
七年级数学
不等式及其性质
引导性材料:
1.据气象预报,某天的最高气温是10℃,最
低气温为-5℃,由此我们说这一天的气温
不低于 ℃,并且不高于 ℃;
2.统计全班同学的年龄,年龄最大者为16岁,
可以知道全班每个同学的年龄都 17岁;
若设物体A的重量为x克;某天的气温为t℃;
本班某同学的年龄为a岁,上述不等关系能用式子
表示出来吗?
-5
10
小于
x>2,x <3,t≥-5,t≤10 ,a <17
-7<-5,3+4>1+4,5+3≠12-5
a+2>a+1,x+3 <6 ,a≠0,
(1)上述式子有哪些表示数量关系的符号?
这些符号表示什么关系?
(2)这些符号两侧的代数式可随意交换
位置吗?
(3)什么叫不等式?
(表示不等关系)
(不可随意互换位置)
(用不等号表示不等关系的式子叫不等式)
练习:
1.判断下列式子哪些是不等式?为什么?
(1)3> 2 (2)a2+1> 0 (3)3x2+2x
(4)x< 2x+1 (5)x=2x-5
(6)x2+4x< 3x+1 (7)a+b≠c
2.用“>”或“<”填空:
(1)4 -6 (2)-1 0 (3)-8 -3 (4)-4.5 -4
(5)7+3 4+3 (6)7+(-3) 4+(-3)
(7)7×3 4×3 (8)7×(-3) 4×(-3)
√
√
√
√
√
>
>
>
>
<
<
<
<
3.用不等式表示:
(1)a是正数
(2)a是负数
(3)x与3的和小于6
(4)x与2的差大于-1
(5)x的4倍大于等于7
(6)y的一半小于3
a>0
a<0
x+3<6
x-2>-1
4x≥7
y<3
解: (1) a<0 ;
(2)a≥0;
(3) 6x-3>10 ;
例1.用不等式表示:
(1) a是负数;(2) a是非负数;
(3) x的6倍减去3大于10;
(4)y的 与6的差小于1;
(5)y的 与6的差不小于1.
(4) y-6<1.
(5) y-6≥1
1.你能检验x=2及x=3是否为方程x+3=6
的解吗?
2.已知数值:-5, 0.5, 3, 0, 2, -2.5, 5.2
(1)判断:上述数值,哪些使不等式x+3<6
成立?哪些使之不成立?
(2)说出几个使不等式x+3<6成立的x的值,
及使之不成立的x的值.
总结:判断不等式是否成立的方法--------
不等号两边的大小关系是否与不等号一致
反馈练习:
1.当x取下列数值时,哪些是不等式
x+3>6解?
-4, -2.5, 0, 1, 3.5, 4, 4.5, 7
2. x=2是不是不等式x+3>4的解?
当x=1.5时呢?当x=-1时呢?
√
√
√
√
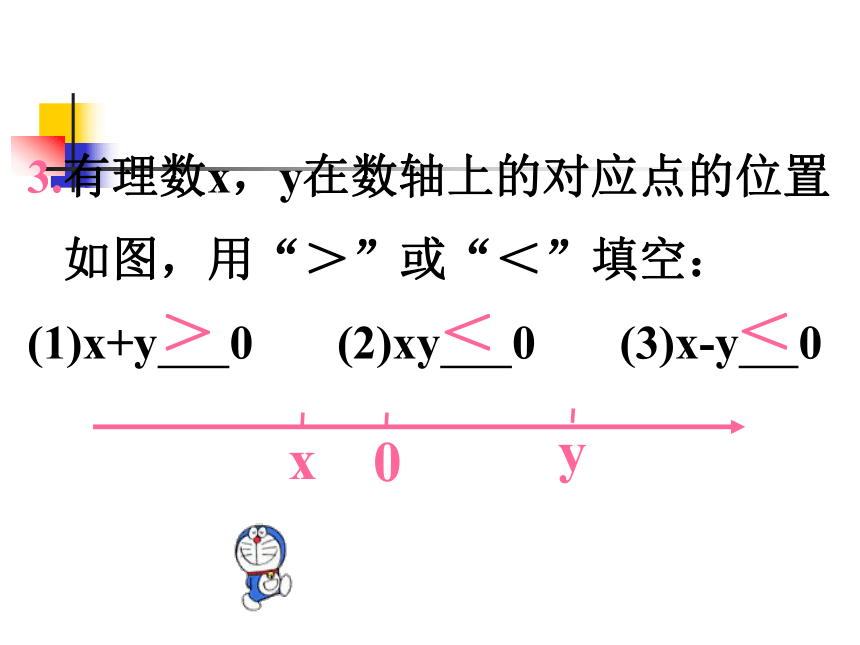
3.有理数x,y在数轴上的对应点的位置
如图,用“>”或“<”填空:
(1)x+y 0 (2)xy 0 (3)x-y 0
0
x
y
>
<
<
4.(1)用不等式表示:x与3的和小于等于6;
解:(1)x+3≤6;
(2)x取-5,0,0.5,2,3时不等式成立;
(3)x≤3时,不等式x+3≤6总成立;
x>3时,不等式x+3≤6总不成立.
(2)写出使上述不等式成立的几个x的值;
(3)x取何值时,不等式x+3≤6总成立? 取何值时总不成立?
5.绝对值小于3的非负整数有 ;
6.下列选项正确的是( )
A. a不是负数,则a>0
B. b是不大于0的数,则b<0;
C. m不小于-1,则m>-1;
D. a+b是负数,则a+b<0.
7.A市某天的最低气温是-7℃,最高气温
是6℃,设这天气温为t℃,则 t满足的
条件是 .
0,1,2
D
-7≤t≤6
8.依题意列不等式:
(1)a的3倍与7的差是非正数;
(2)x与6的和大于9且小于12.
解:(1)3a-7≤0
(2)9<x+6<12
小结:
1.掌握不等式是否成立的判断方法;
2.依题意列出正确的不等式.
(注意:表示不等关系的词语要用
不等号来表示,“不大于”即“≤”,
“不小于”即“≥” )
1.什么是等式?
2.等式的基本性质是什么?
3.用“>”或“<”填空:
7 + 3 4 + 3 7 +(-3) 4 +(-3)
7×3 4×3 7×(-3) 4×(-3)
(1)上述不等式中哪题的不等号与7>4
一致?
(2)观察思考,猜出不等式的基本性质
>
>
>
<
不等式的三条基本性质:
1. 不等式两边都加上(或减去)同一个
数或同一个整式,不等号的方向不变;
2. 不等式两边都乘(或除以)同一个
正数,不等号的方向不变;
3.*不等式两边都乘(或除以)同一个
负数,不等号的方向改变 ;
---如何用数学语言表示?
---与等式的基本性质有什么联系与区别?
解:(1)根据不等式基本性质1,两边都
加上2,得 x-2+2<3+2
x<5
(2)根据不等式基本性质1,两边都减去5x,
得 6x-5x<5x-1-5x
x<-1
例1.根据不等式的基本性质,把下列
不等式化成x<a或x>a的形式:
(1) x-2< 3 (2) 6x< 5x-1
(3) x>5 (4) -4x>3
例2.设a>b,用“<”或“>”填空:
(1)a-3 b-3 (2) (3) -4a -4b
解:(1) ∵a>b
∴两边都减去3,由不等式基本性质1
得 a-3>b-3
(2) ∵a>b,并且2>0
∴两边都除以2,由不等式基本性质2
得
(3) ∵a>b,并且-4<0
∴两边都乘以-4,由不等式基本性质3
得 -4a<-4b
>
变式训练:
1.用“>”或“<”在横线上填空,并在题后
括号内填写理由.
∵a>b (2)∵ a>b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m>5n (4)∵4x>5x
∴ -m ( ) ∴ x 0( )
(5)∵ < (6)∵a-1<8
∴ a 2b( ) ∴ a 9( )
>
>
>
<
<
<
不等式基
本性质1
不等式基
本性质3
不等式基
本性质3
不等式基
本性质1
不等式基
本性质2
不等式基
本性质1
2.单项选择:
(1)由 x>y 得 ax>ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
(2)由 x>y 得 ax≤ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
(3)由 a>b 得 am2>bm2 的条件是( )
A.m>0 B.m<0 C.m≠0 D.m是任意有理数
(4)若 a>1,则下列各式中错误的是( )
A.4a>4 B.a+5>6 C. < D.a-1<0
A
D
C
D
3.判断正误:
(1)∵a+8>4 (2)∵3>2
∴a>-4 ( ) ∴3a>2a( )
(3)∵-1>-2 (4)∵ab>0
∴a-1>a-2 ( ) ∴a>0,b> 0( )
√
×
√
×
归纳小结:
1.本节重点
(1)掌握不等式的三条基本性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;
2.注意事项
(1)要反复对比不等式性质与等式性质
的异同点;
(2)当不等式两边都乘以(或除以)同
一个数时,一定要看清是正数还是
负数;对于未给定范围的字母,应
分情况讨论.
七年级数学
不等式及其性质
引导性材料:
1.据气象预报,某天的最高气温是10℃,最
低气温为-5℃,由此我们说这一天的气温
不低于 ℃,并且不高于 ℃;
2.统计全班同学的年龄,年龄最大者为16岁,
可以知道全班每个同学的年龄都 17岁;
若设物体A的重量为x克;某天的气温为t℃;
本班某同学的年龄为a岁,上述不等关系能用式子
表示出来吗?
-5
10
小于
x>2,x <3,t≥-5,t≤10 ,a <17
-7<-5,3+4>1+4,5+3≠12-5
a+2>a+1,x+3 <6 ,a≠0,
(1)上述式子有哪些表示数量关系的符号?
这些符号表示什么关系?
(2)这些符号两侧的代数式可随意交换
位置吗?
(3)什么叫不等式?
(表示不等关系)
(不可随意互换位置)
(用不等号表示不等关系的式子叫不等式)
练习:
1.判断下列式子哪些是不等式?为什么?
(1)3> 2 (2)a2+1> 0 (3)3x2+2x
(4)x< 2x+1 (5)x=2x-5
(6)x2+4x< 3x+1 (7)a+b≠c
2.用“>”或“<”填空:
(1)4 -6 (2)-1 0 (3)-8 -3 (4)-4.5 -4
(5)7+3 4+3 (6)7+(-3) 4+(-3)
(7)7×3 4×3 (8)7×(-3) 4×(-3)
√
√
√
√
√
>
>
>
>
<
<
<
<
3.用不等式表示:
(1)a是正数
(2)a是负数
(3)x与3的和小于6
(4)x与2的差大于-1
(5)x的4倍大于等于7
(6)y的一半小于3
a>0
a<0
x+3<6
x-2>-1
4x≥7
y<3
解: (1) a<0 ;
(2)a≥0;
(3) 6x-3>10 ;
例1.用不等式表示:
(1) a是负数;(2) a是非负数;
(3) x的6倍减去3大于10;
(4)y的 与6的差小于1;
(5)y的 与6的差不小于1.
(4) y-6<1.
(5) y-6≥1
1.你能检验x=2及x=3是否为方程x+3=6
的解吗?
2.已知数值:-5, 0.5, 3, 0, 2, -2.5, 5.2
(1)判断:上述数值,哪些使不等式x+3<6
成立?哪些使之不成立?
(2)说出几个使不等式x+3<6成立的x的值,
及使之不成立的x的值.
总结:判断不等式是否成立的方法--------
不等号两边的大小关系是否与不等号一致
反馈练习:
1.当x取下列数值时,哪些是不等式
x+3>6解?
-4, -2.5, 0, 1, 3.5, 4, 4.5, 7
2. x=2是不是不等式x+3>4的解?
当x=1.5时呢?当x=-1时呢?
√
√
√
√
3.有理数x,y在数轴上的对应点的位置
如图,用“>”或“<”填空:
(1)x+y 0 (2)xy 0 (3)x-y 0
0
x
y
>
<
<
4.(1)用不等式表示:x与3的和小于等于6;
解:(1)x+3≤6;
(2)x取-5,0,0.5,2,3时不等式成立;
(3)x≤3时,不等式x+3≤6总成立;
x>3时,不等式x+3≤6总不成立.
(2)写出使上述不等式成立的几个x的值;
(3)x取何值时,不等式x+3≤6总成立? 取何值时总不成立?
5.绝对值小于3的非负整数有 ;
6.下列选项正确的是( )
A. a不是负数,则a>0
B. b是不大于0的数,则b<0;
C. m不小于-1,则m>-1;
D. a+b是负数,则a+b<0.
7.A市某天的最低气温是-7℃,最高气温
是6℃,设这天气温为t℃,则 t满足的
条件是 .
0,1,2
D
-7≤t≤6
8.依题意列不等式:
(1)a的3倍与7的差是非正数;
(2)x与6的和大于9且小于12.
解:(1)3a-7≤0
(2)9<x+6<12
小结:
1.掌握不等式是否成立的判断方法;
2.依题意列出正确的不等式.
(注意:表示不等关系的词语要用
不等号来表示,“不大于”即“≤”,
“不小于”即“≥” )
1.什么是等式?
2.等式的基本性质是什么?
3.用“>”或“<”填空:
7 + 3 4 + 3 7 +(-3) 4 +(-3)
7×3 4×3 7×(-3) 4×(-3)
(1)上述不等式中哪题的不等号与7>4
一致?
(2)观察思考,猜出不等式的基本性质
>
>
>
<
不等式的三条基本性质:
1. 不等式两边都加上(或减去)同一个
数或同一个整式,不等号的方向不变;
2. 不等式两边都乘(或除以)同一个
正数,不等号的方向不变;
3.*不等式两边都乘(或除以)同一个
负数,不等号的方向改变 ;
---如何用数学语言表示?
---与等式的基本性质有什么联系与区别?
解:(1)根据不等式基本性质1,两边都
加上2,得 x-2+2<3+2
x<5
(2)根据不等式基本性质1,两边都减去5x,
得 6x-5x<5x-1-5x
x<-1
例1.根据不等式的基本性质,把下列
不等式化成x<a或x>a的形式:
(1) x-2< 3 (2) 6x< 5x-1
(3) x>5 (4) -4x>3
例2.设a>b,用“<”或“>”填空:
(1)a-3 b-3 (2) (3) -4a -4b
解:(1) ∵a>b
∴两边都减去3,由不等式基本性质1
得 a-3>b-3
(2) ∵a>b,并且2>0
∴两边都除以2,由不等式基本性质2
得
(3) ∵a>b,并且-4<0
∴两边都乘以-4,由不等式基本性质3
得 -4a<-4b
>
变式训练:
1.用“>”或“<”在横线上填空,并在题后
括号内填写理由.
∵a>b (2)∵ a>b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m>5n (4)∵4x>5x
∴ -m ( ) ∴ x 0( )
(5)∵ < (6)∵a-1<8
∴ a 2b( ) ∴ a 9( )
>
>
>
<
<
<
不等式基
本性质1
不等式基
本性质3
不等式基
本性质3
不等式基
本性质1
不等式基
本性质2
不等式基
本性质1
2.单项选择:
(1)由 x>y 得 ax>ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
(2)由 x>y 得 ax≤ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
(3)由 a>b 得 am2>bm2 的条件是( )
A.m>0 B.m<0 C.m≠0 D.m是任意有理数
(4)若 a>1,则下列各式中错误的是( )
A.4a>4 B.a+5>6 C. < D.a-1<0
A
D
C
D
3.判断正误:
(1)∵a+8>4 (2)∵3>2
∴a>-4 ( ) ∴3a>2a( )
(3)∵-1>-2 (4)∵ab>0
∴a-1>a-2 ( ) ∴a>0,b> 0( )
√
×
√
×
归纳小结:
1.本节重点
(1)掌握不等式的三条基本性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;
2.注意事项
(1)要反复对比不等式性质与等式性质
的异同点;
(2)当不等式两边都乘以(或除以)同
一个数时,一定要看清是正数还是
负数;对于未给定范围的字母,应
分情况讨论.
