数学:10.3《平行线的性质》课件(沪科版七年级下)
文档属性
| 名称 | 数学:10.3《平行线的性质》课件(沪科版七年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 183.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-15 20:52:12 | ||
图片预览



文档简介
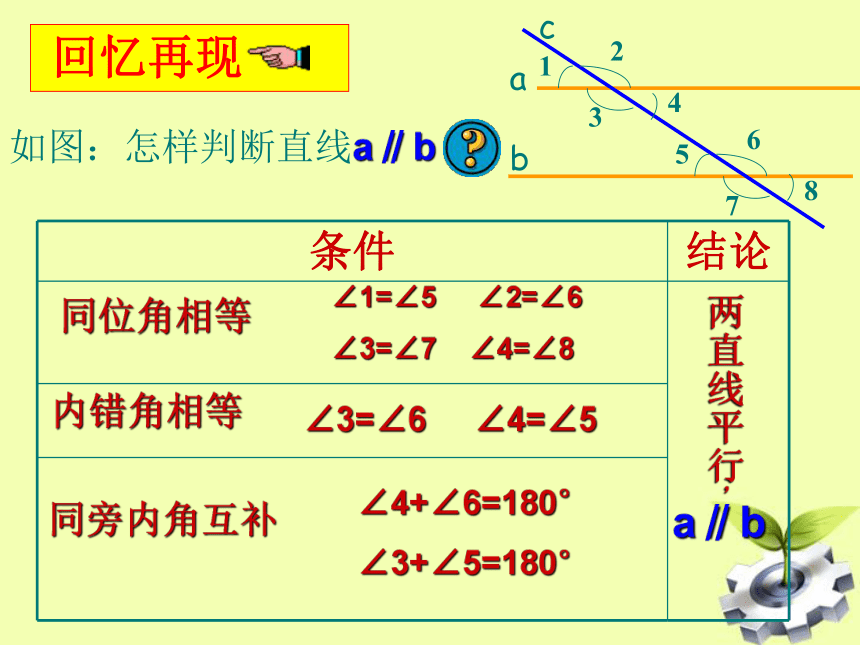
(共10张PPT)
b
1
2
3
4
5
6
7
8
a
c
条件
结论
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
∠3=∠6
∠4=∠5
∠4+∠6=180°
∠3+∠5=180°
a∥b
内错角相等
同旁内角互补
同位角相等
回忆再现
如图:怎样判断直线a∥b
两直线平行,
b
1
2
3
4
5
6
7
8
a
c
如图:直线
a
与b
直线平行
(1)比较同位角∠1和∠5的大小,它们相等吗?
相等:∠1=∠5
图中还有其它同位角吗?它们的大小有什么关系?
∠2=∠6
∠3=∠7
∠4=∠8
还有三对同位角.
(2)图中有几对内错角?它们的大小有什么关系?为什么?
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
有两对内错角.
∠3=∠6
∠4=∠5
∵∠2=∠3,∠2=∠6
∴
∠3=∠6
同理:
∠4=∠5
有两对同旁内角.
∠4+∠6=180°
∠3+∠5=180°
从中,你发现了什么规律吗?
规律:
两条平行直线被第三条直线直线所截,同位角相等,内错角相等,同旁内角互补.
简记为:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
a
b
c
如图:一束平行光线AB和DE射向一个水平镜面后被反射,此时∠1=∠2
,
∠3=∠4
。
1
2
3
4
B
E
A
C
D
F
(1
)∠1、∠3的大小有什么关系?
∠2与∠4呢?
因为AB∥DE
,所以∠1=∠3.
相等
两直线平行
同位角相等
(2)发射光线BC与EF也平行吗?
因为
∠2=∠4
,所以
BC∥EF
.
平行
同位角相等
两直线平行
因为
∠1=∠3
且
∠1=∠2
,∠3=∠4,
所以
∠2=∠4
.
你知道理由吗
1、如图,是有梯形上底的一部分,已经量得∠A=115o,∠D=100o,梯形另外两个角各是多少度?
解:因为AD∥BC,(梯形定义)
所以∠A+∠B=180o.
∠C=180o-100o=80o.
所以梯形的另外两个角分别是65o和80o.
(两直线平行,同旁内角互补)
(等式性质1)
D
C
B
A
于是∠B=180o-115o=65o.
∠D+∠C=180o.
(两直线平行,同旁内角互补)
(等式性质1)
(1)因为∠ADE=∠B=60o,(已知)
所以DE∥BC.(同位角相等,两直线平行)
(2)因为DE∥BC,(已证)
所以∠C=∠AED=40o.(两直线平行,同位角相等)
解答
如图,已知D是AB上一点,E是AC上一点,∠ADE=60o,∠B=60o,∠AED=40o,
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
E
D
C
B
A
问题
本节课学行线的三个特征(性质)
,总结了平行线的判定与性质的区别.
条件:角的关系
平行关系
特征:平行关系
角的关系
本节课初步学习了如何应用平行线的识别与特征进行计算和说理(证明).
要懂得几何中的计算往往要说理,要熟悉几何里计算题的格式;
还要懂得几何中常常可以由“已知”的条件推得一系列新的结论,在这个过程中,要能清楚每一步推理的依据,并初步了解解答这类问题的格式和要求.
b
1
2
3
4
5
6
7
8
a
c
条件
结论
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
∠3=∠6
∠4=∠5
∠4+∠6=180°
∠3+∠5=180°
a∥b
内错角相等
同旁内角互补
同位角相等
回忆再现
如图:怎样判断直线a∥b
两直线平行,
b
1
2
3
4
5
6
7
8
a
c
如图:直线
a
与b
直线平行
(1)比较同位角∠1和∠5的大小,它们相等吗?
相等:∠1=∠5
图中还有其它同位角吗?它们的大小有什么关系?
∠2=∠6
∠3=∠7
∠4=∠8
还有三对同位角.
(2)图中有几对内错角?它们的大小有什么关系?为什么?
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
有两对内错角.
∠3=∠6
∠4=∠5
∵∠2=∠3,∠2=∠6
∴
∠3=∠6
同理:
∠4=∠5
有两对同旁内角.
∠4+∠6=180°
∠3+∠5=180°
从中,你发现了什么规律吗?
规律:
两条平行直线被第三条直线直线所截,同位角相等,内错角相等,同旁内角互补.
简记为:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
a
b
c
如图:一束平行光线AB和DE射向一个水平镜面后被反射,此时∠1=∠2
,
∠3=∠4
。
1
2
3
4
B
E
A
C
D
F
(1
)∠1、∠3的大小有什么关系?
∠2与∠4呢?
因为AB∥DE
,所以∠1=∠3.
相等
两直线平行
同位角相等
(2)发射光线BC与EF也平行吗?
因为
∠2=∠4
,所以
BC∥EF
.
平行
同位角相等
两直线平行
因为
∠1=∠3
且
∠1=∠2
,∠3=∠4,
所以
∠2=∠4
.
你知道理由吗
1、如图,是有梯形上底的一部分,已经量得∠A=115o,∠D=100o,梯形另外两个角各是多少度?
解:因为AD∥BC,(梯形定义)
所以∠A+∠B=180o.
∠C=180o-100o=80o.
所以梯形的另外两个角分别是65o和80o.
(两直线平行,同旁内角互补)
(等式性质1)
D
C
B
A
于是∠B=180o-115o=65o.
∠D+∠C=180o.
(两直线平行,同旁内角互补)
(等式性质1)
(1)因为∠ADE=∠B=60o,(已知)
所以DE∥BC.(同位角相等,两直线平行)
(2)因为DE∥BC,(已证)
所以∠C=∠AED=40o.(两直线平行,同位角相等)
解答
如图,已知D是AB上一点,E是AC上一点,∠ADE=60o,∠B=60o,∠AED=40o,
(1)DE和BC平行吗?为什么?
(2)∠C是多少度?为什么?
E
D
C
B
A
问题
本节课学行线的三个特征(性质)
,总结了平行线的判定与性质的区别.
条件:角的关系
平行关系
特征:平行关系
角的关系
本节课初步学习了如何应用平行线的识别与特征进行计算和说理(证明).
要懂得几何中的计算往往要说理,要熟悉几何里计算题的格式;
还要懂得几何中常常可以由“已知”的条件推得一系列新的结论,在这个过程中,要能清楚每一步推理的依据,并初步了解解答这类问题的格式和要求.
