数学:7.1《不等式的性质》课件(沪科版七年级下)
文档属性
| 名称 | 数学:7.1《不等式的性质》课件(沪科版七年级下) |  | |
| 格式 | zip | ||
| 文件大小 | 687.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-15 20:52:12 | ||
图片预览



文档简介
(共10张PPT)
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
由此可见,“不相等”处处可见.
从今天起,我们开始学习一类新的数学知识:不等式.
不相等 处处可见
1
不等关系
自学提纲
1.认真看书中的内容.
2.举出生活中一个不等量关系的例子.
3.注意表示不等关系的词语如“不大于”,
“不高于”等等.
4.熟练掌握不等式基本性质1、基本性质2和基本性质3.
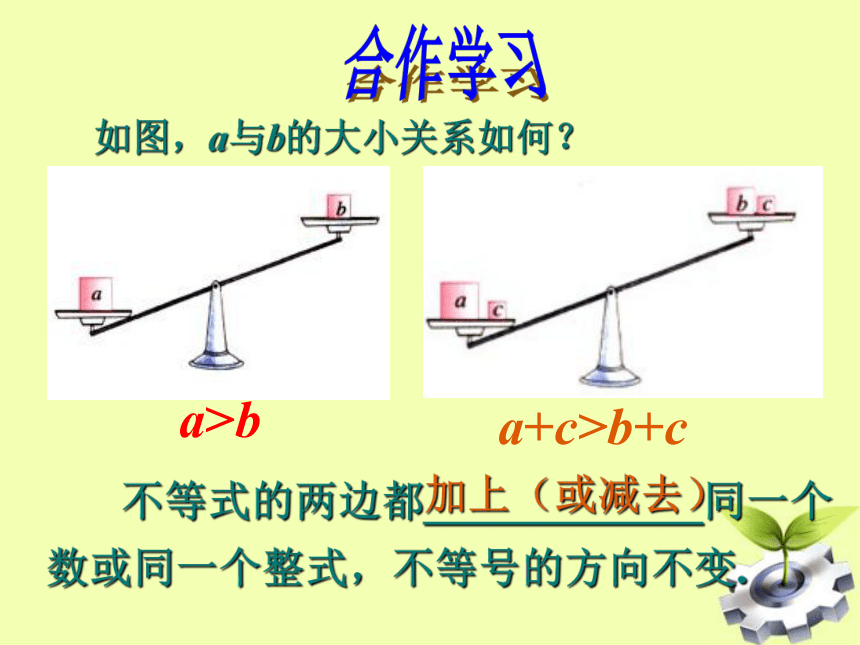
如图,a与b的大小关系如何?
不等式的两边都_____________同一个数或同一个整式,不等号的方向不变.
a>b
a+c>b+c
加上(或减去)
观察:用“<”或“>”填空,并找一找其中的规律.
8__12
8×4__12×4
8÷4__12÷4
(-4)__(-6)
(-4)×2__(-6)×2
(-4)÷2__(-6)÷2
想一想: 你发现了什么规律
不等式的两边都乘以(或除以)同一个正数,不等号的方向____;而乘以(除以)同一个负数,不等号的方向_____.
改变
不变
8×(-4)__12×(-4)
8÷(-4)__12÷(-4)
(-4)×(-2)__(-6)×(-2)
(-4)÷(-2)__(-6)÷(-2)
<
<
<
<
<
>
>
>
>
>
不等式的基本性质1:
不等式的两边都加上(或减去)同一个整式,不等号的方向不变.
不等式的基本性质2:
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3:
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
针对练习
自学检测
1.如果x-5>4,那么两边都 可得到x>9
2.如果在-7<8的两边都加上9,可得到
3.如果在5>-2的两边都加上a+2,可得到
4.如果在-3>-4的两边都乘以7,可得到
5.如果在8>0的两边都乘以8,可得到
6.如果在 的两边都乘以14,
可得到
X
7
>2+
X
2
加上5
2 < 17
a+7 > a
-21>-28
64 > 0
2x>28+7x
1.如果在不等式8>0的两边都乘以―8可得到
2.如果-3x>9,那么两边都除以―3可得到
3.设m>n,用“>”或“<”填空:
m-5 n-5(根据不等式的性质 )
-6m -6n(根据不等式的性质 )
针对练习
-64 < 0
x < -3
>
1
<
3
今天我学会了……
28
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
由此可见,“不相等”处处可见.
从今天起,我们开始学习一类新的数学知识:不等式.
不相等 处处可见
1
不等关系
自学提纲
1.认真看书中的内容.
2.举出生活中一个不等量关系的例子.
3.注意表示不等关系的词语如“不大于”,
“不高于”等等.
4.熟练掌握不等式基本性质1、基本性质2和基本性质3.
如图,a与b的大小关系如何?
不等式的两边都_____________同一个数或同一个整式,不等号的方向不变.
a>b
a+c>b+c
加上(或减去)
观察:用“<”或“>”填空,并找一找其中的规律.
8__12
8×4__12×4
8÷4__12÷4
(-4)__(-6)
(-4)×2__(-6)×2
(-4)÷2__(-6)÷2
想一想: 你发现了什么规律
不等式的两边都乘以(或除以)同一个正数,不等号的方向____;而乘以(除以)同一个负数,不等号的方向_____.
改变
不变
8×(-4)__12×(-4)
8÷(-4)__12÷(-4)
(-4)×(-2)__(-6)×(-2)
(-4)÷(-2)__(-6)÷(-2)
<
<
<
<
<
>
>
>
>
>
不等式的基本性质1:
不等式的两边都加上(或减去)同一个整式,不等号的方向不变.
不等式的基本性质2:
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3:
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
针对练习
自学检测
1.如果x-5>4,那么两边都 可得到x>9
2.如果在-7<8的两边都加上9,可得到
3.如果在5>-2的两边都加上a+2,可得到
4.如果在-3>-4的两边都乘以7,可得到
5.如果在8>0的两边都乘以8,可得到
6.如果在 的两边都乘以14,
可得到
X
7
>2+
X
2
加上5
2 < 17
a+7 > a
-21>-28
64 > 0
2x>28+7x
1.如果在不等式8>0的两边都乘以―8可得到
2.如果-3x>9,那么两边都除以―3可得到
3.设m>n,用“>”或“<”填空:
m-5 n-5(根据不等式的性质 )
-6m -6n(根据不等式的性质 )
针对练习
-64 < 0
x < -3
>
1
<
3
今天我学会了……
28
