13.2可能性(第2课时)课件(苏科版七年级下)(22张)
文档属性
| 名称 | 13.2可能性(第2课时)课件(苏科版七年级下)(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 376.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-15 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
飞机失事会给旅客造成意外伤害。一家保险公司要为购买机票的旅客进行保险,应该向旅客收取多少保费呢?为此保险公司必须精确计算出飞机失事的可能性有多大.
类似这样的问题在我们的日常生活中也经常遇到.例如:
抛掷1枚均匀硬币,正面朝上.
在装有彩球的袋子中,任意摸出的1个球恰好是红球.
明天将会下雨.
抛掷1枚均匀骰子,6点朝上.
……
都是随机事件,你还能再举出一些随机事件吗?
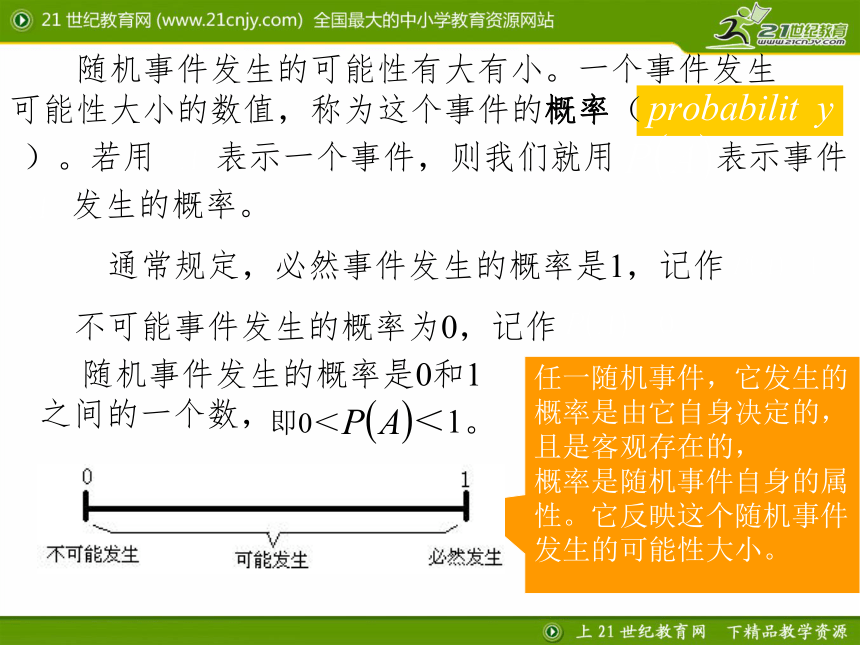
随机事件发生的可能性有大有小。一个事件发生可能性大小的数值,称为这个事件的概率(
)。若用
表示一个事件,则我们就用
表示事件
发生的概率。
随机事件发生的概率是0和1
之间的一个数,
通常规定,必然事件发生的概率是1,记作
不可能事件发生的概率为0,记作
即0< <1。
任一随机事件,它发生的概率是由它自身决定的,且是客观存在的,
概率是随机事件自身的属性。它反映这个随机事件发生的可能性大小。
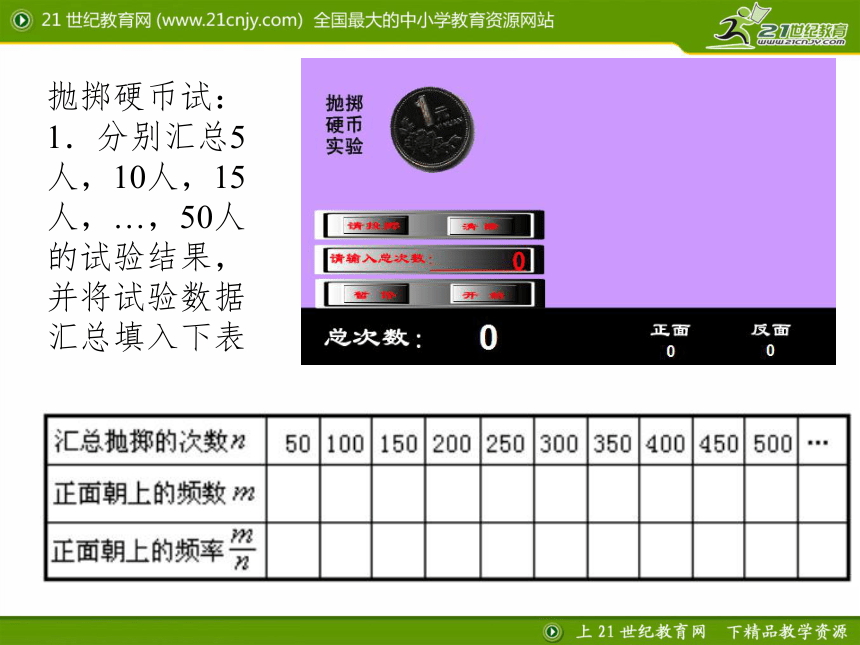
抛掷硬币试:
1.分别汇总5人,10人,15人,…,50人的试验结果,并将试验数据汇总填入下表
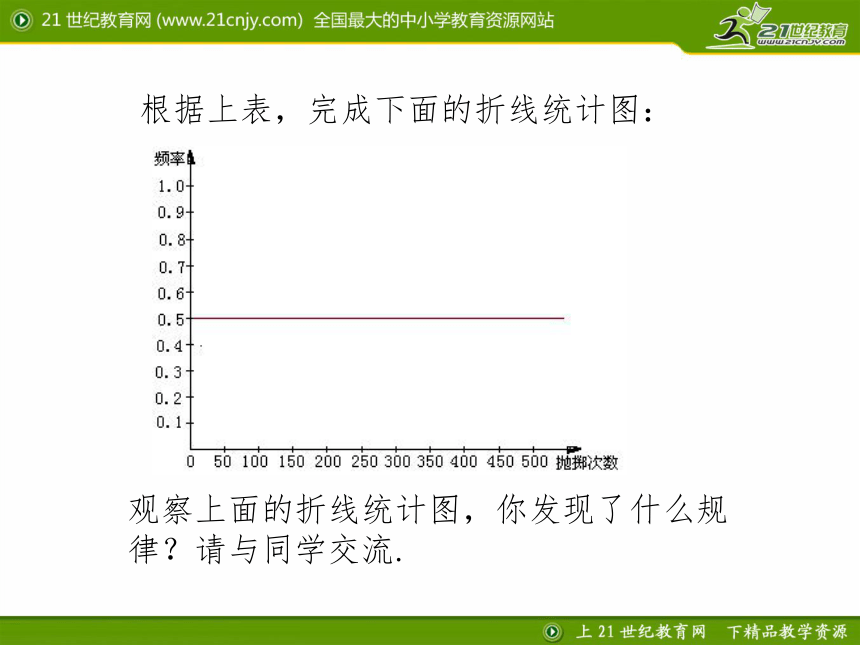
根据上表,完成下面的折线统计图:
观察上面的折线统计图,你发现了什么规律?请与同学交流.
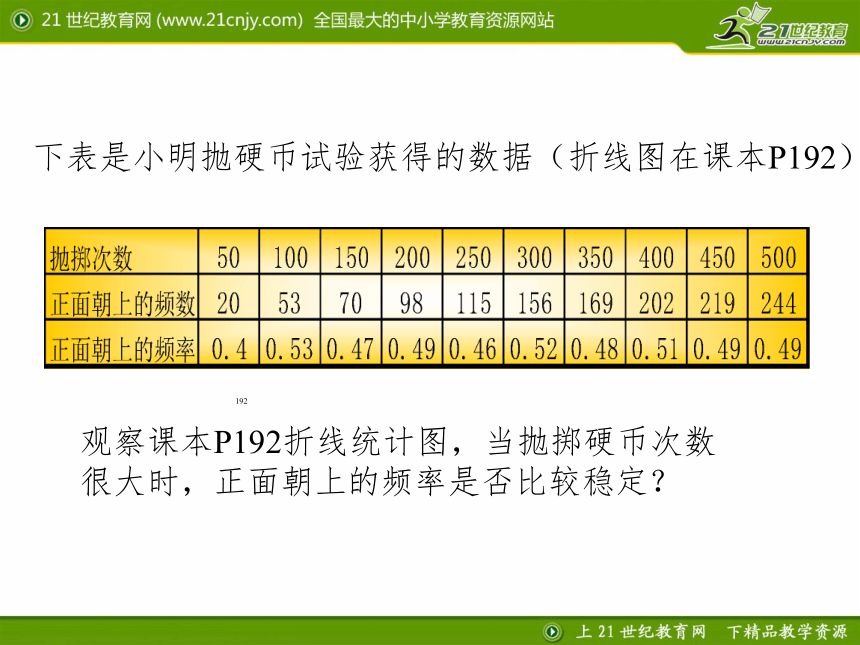
下表是小明抛硬币试验获得的数据(折线图在课本P192)
观察课本P192折线统计图,当抛掷硬币次数很大时,正面朝上的频率是否比较稳定?
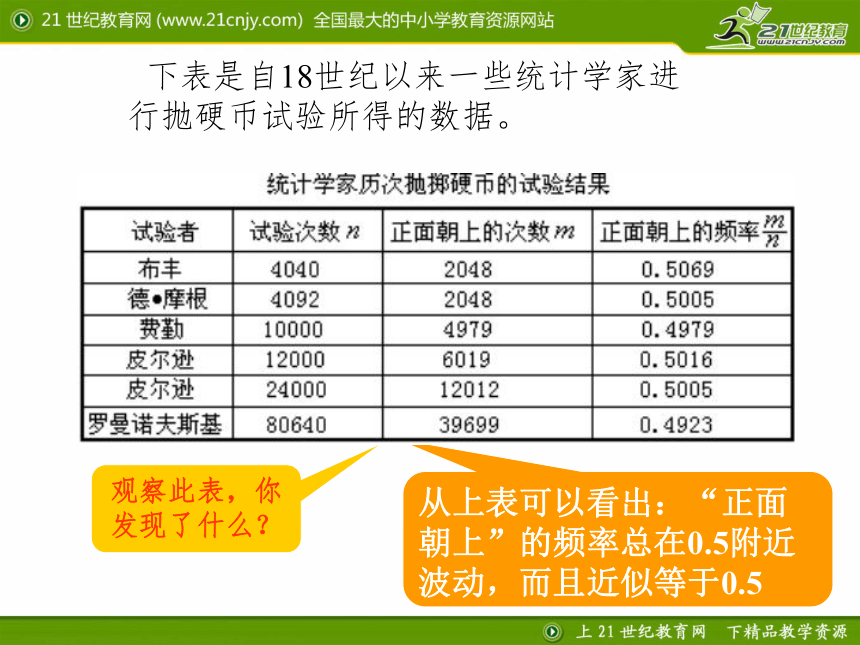
下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据。
观察此表,你发现了什么?
从上表可以看出:“正面朝上”的频率总在0.5附近波动,而且近似等于0.5
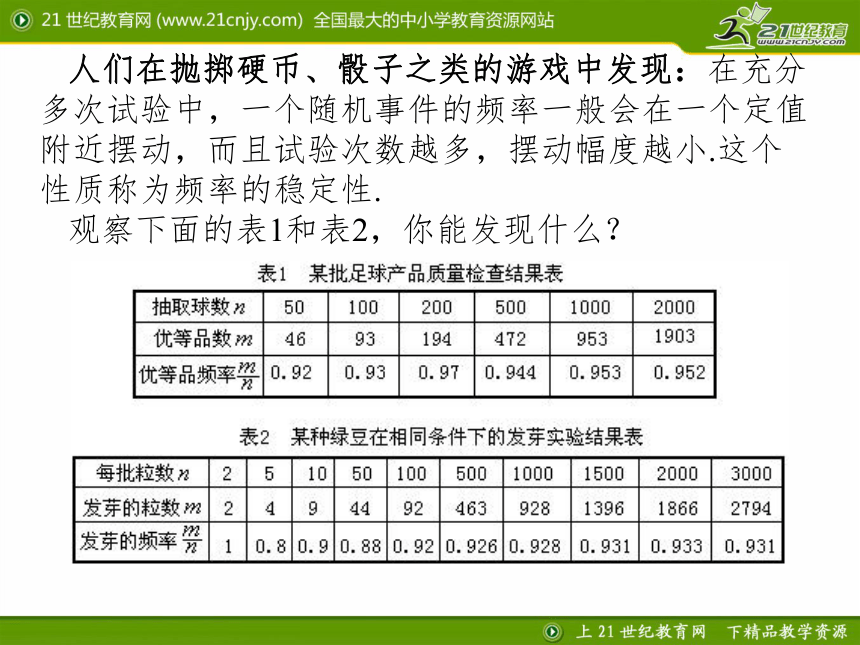
人们在抛掷硬币、骰子之类的游戏中发现:在充分多次试验中,一个随机事件的频率一般会在一个定值附近摆动,而且试验次数越多,摆动幅度越小.这个性质称为频率的稳定性.
观察下面的表1和表2,你能发现什么?
从表1可以看到,当抽查的足球数很多时,抽到优等品的频率 接近于某一个常数,并在它附近摆动。
从表2可以看到,当实验的绿豆的粒数很多时,绿豆发芽的频率 接近于某一个常数,并在它附近摆动。
一般地,在一定条件下大量重复进行同一试验时,事件A发生的频率 会稳定地在某一个常数附近摆动,这个常数就是事件A发生的概率
事实上,事件A发生的概率 的精确值,即这个常数还是未知的,但是在实际工作中,人们常把试验次数很大时事件发生的频率作为概率的近似值.
练一练:P194
1) 若袋中有3个红球、1个白球,同学们认为这名同学任摸一球,摸出的球可能是什么颜色?与同伴进行交流。
2)若将每个球都编上号码,分别为1号球(红)、2号球(红)、3号球(红)、4号球(白),那么这位同学摸到每个球的可能性一样吗?
3)任意摸出一球,你能说出所有可能出现的结果吗?
所有可能出现的结果有:1号球、2号球、3号球、4号球,摸到红球的可能出现的结果有:1号球、2号球、3号球。
人们通常用
来表示摸到红球的可能性,也叫做摸到红球的概率(probability).概率用英文(probability)的第一个字母p来表示.
1)你能写出摸到白球的概率吗?
解:P(摸到白球)=
-
1
4
2)若把摸球游戏换成4个红球,那么摸到红球、白球的概率分别是多少?
解:P(摸到红球)=1,
P(摸到白球)=0
3)你能写出必然事件和不可能事件的
概率吗?
4)你能猜出不确定事件的概率的范围
吗?
例1.掷一枚均匀的小立方体(立方体的每个面上分标有1点,2点,3点,4点,5点,6点),“6点”朝上的概率是多少?
解:任意掷一枚均匀的小立方体,所有可能出现的结果有6种:“1点”朝上,“2点”朝上,“3点”朝上,“4点”朝上,“5点”朝上,“6点”朝上,每一种结果出现的概率都相等。其中“6点”朝上的结果只有1种,因此
P(“6点”朝上)=
-
1
6
1.在我们班中任意抽取1人做游戏,
你被抽到的概率是多少?
2.一副扑克牌(去掉大、小王),任意抽取其中一张,抽到方块的概率是多少?抽到黑桃的概率呢?
解:P(抽到方块)=
P(抽到黑桃)=
-
13
52
-
1
4
=
=
-
1
4
-
13
52
1
2
-
1
2
-
1
2
-
1
4
-
用
4
个除颜色外完全相同的球设计一个摸球游戏
.
1)使摸到白球的概率为
,摸到红球的概率为
;
2)摸到白球的概率为
,摸到红球的概率为
;
你能用
8
个除颜色外完全相同的球分别设计满
足如上条件的游戏吗?
(1)举出日常生活中你所见到的“概率现象”。
(2)甲产品合格率为98%,乙产品的合格率为 80% ,你认为买哪一种产品更可靠?
(3)阿强在一次抽奖活动中,只抽了一张,就中了一等奖,能不能说这次抽奖活动的中奖率为百分之百?为什么?
(1) 从一副扑克牌(除去大小王)中任抽一张.
P (抽到红心) = ;
1
4
-
P (抽到黑桃) = ;
1
4
-
P (抽到红心3)= ;
1
-
52
1
-
13
P (抽到5)= .
(2)有5张数字卡片,它们的背面完全相同,正面分别标有1,2,2,3,4。现将它们的背面朝上,从中任意摸到一张卡片,则:
P(摸到1号卡片)=
1
-
5
p (摸到2号卡片)= ;
2
-
5
p (摸到3号卡片)= ;
1
-
5
p (摸到4号卡片)= ;
1
-
5
p (摸到奇数号卡片)= ;
2
-
5
P(摸到偶数号卡片) = .
3
-
5
(1)袋子里有1个红球,3个白球和5个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则
P(摸到红球)= ;
P(摸到白球)= ;
P(摸到黄球)= .
1
-
9
1
-
3
5
-
9
( 2 )任意翻一下2004年日历,
翻出1月6日的概率为 ;翻
出4月31日的概
率为 .
1/366
0
课堂小结:
1.预测随机事件在每一次实验中发生的可能性,可以预先估计随机事件在每一次实验中发生的机会有多大,不发生的机会机会有多大.
随机事件的发生与不发生的机会不总是对半的(都为50%),应通过开展一系列数学实践活动从中掌握预测的一些规律.
P
作业习题13.2
祝同学们
祝同学们
进步
进步
飞机失事会给旅客造成意外伤害。一家保险公司要为购买机票的旅客进行保险,应该向旅客收取多少保费呢?为此保险公司必须精确计算出飞机失事的可能性有多大.
类似这样的问题在我们的日常生活中也经常遇到.例如:
抛掷1枚均匀硬币,正面朝上.
在装有彩球的袋子中,任意摸出的1个球恰好是红球.
明天将会下雨.
抛掷1枚均匀骰子,6点朝上.
……
都是随机事件,你还能再举出一些随机事件吗?
随机事件发生的可能性有大有小。一个事件发生可能性大小的数值,称为这个事件的概率(
)。若用
表示一个事件,则我们就用
表示事件
发生的概率。
随机事件发生的概率是0和1
之间的一个数,
通常规定,必然事件发生的概率是1,记作
不可能事件发生的概率为0,记作
即0< <1。
任一随机事件,它发生的概率是由它自身决定的,且是客观存在的,
概率是随机事件自身的属性。它反映这个随机事件发生的可能性大小。
抛掷硬币试:
1.分别汇总5人,10人,15人,…,50人的试验结果,并将试验数据汇总填入下表
根据上表,完成下面的折线统计图:
观察上面的折线统计图,你发现了什么规律?请与同学交流.
下表是小明抛硬币试验获得的数据(折线图在课本P192)
观察课本P192折线统计图,当抛掷硬币次数很大时,正面朝上的频率是否比较稳定?
下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据。
观察此表,你发现了什么?
从上表可以看出:“正面朝上”的频率总在0.5附近波动,而且近似等于0.5
人们在抛掷硬币、骰子之类的游戏中发现:在充分多次试验中,一个随机事件的频率一般会在一个定值附近摆动,而且试验次数越多,摆动幅度越小.这个性质称为频率的稳定性.
观察下面的表1和表2,你能发现什么?
从表1可以看到,当抽查的足球数很多时,抽到优等品的频率 接近于某一个常数,并在它附近摆动。
从表2可以看到,当实验的绿豆的粒数很多时,绿豆发芽的频率 接近于某一个常数,并在它附近摆动。
一般地,在一定条件下大量重复进行同一试验时,事件A发生的频率 会稳定地在某一个常数附近摆动,这个常数就是事件A发生的概率
事实上,事件A发生的概率 的精确值,即这个常数还是未知的,但是在实际工作中,人们常把试验次数很大时事件发生的频率作为概率的近似值.
练一练:P194
1) 若袋中有3个红球、1个白球,同学们认为这名同学任摸一球,摸出的球可能是什么颜色?与同伴进行交流。
2)若将每个球都编上号码,分别为1号球(红)、2号球(红)、3号球(红)、4号球(白),那么这位同学摸到每个球的可能性一样吗?
3)任意摸出一球,你能说出所有可能出现的结果吗?
所有可能出现的结果有:1号球、2号球、3号球、4号球,摸到红球的可能出现的结果有:1号球、2号球、3号球。
人们通常用
来表示摸到红球的可能性,也叫做摸到红球的概率(probability).概率用英文(probability)的第一个字母p来表示.
1)你能写出摸到白球的概率吗?
解:P(摸到白球)=
-
1
4
2)若把摸球游戏换成4个红球,那么摸到红球、白球的概率分别是多少?
解:P(摸到红球)=1,
P(摸到白球)=0
3)你能写出必然事件和不可能事件的
概率吗?
4)你能猜出不确定事件的概率的范围
吗?
例1.掷一枚均匀的小立方体(立方体的每个面上分标有1点,2点,3点,4点,5点,6点),“6点”朝上的概率是多少?
解:任意掷一枚均匀的小立方体,所有可能出现的结果有6种:“1点”朝上,“2点”朝上,“3点”朝上,“4点”朝上,“5点”朝上,“6点”朝上,每一种结果出现的概率都相等。其中“6点”朝上的结果只有1种,因此
P(“6点”朝上)=
-
1
6
1.在我们班中任意抽取1人做游戏,
你被抽到的概率是多少?
2.一副扑克牌(去掉大、小王),任意抽取其中一张,抽到方块的概率是多少?抽到黑桃的概率呢?
解:P(抽到方块)=
P(抽到黑桃)=
-
13
52
-
1
4
=
=
-
1
4
-
13
52
1
2
-
1
2
-
1
2
-
1
4
-
用
4
个除颜色外完全相同的球设计一个摸球游戏
.
1)使摸到白球的概率为
,摸到红球的概率为
;
2)摸到白球的概率为
,摸到红球的概率为
;
你能用
8
个除颜色外完全相同的球分别设计满
足如上条件的游戏吗?
(1)举出日常生活中你所见到的“概率现象”。
(2)甲产品合格率为98%,乙产品的合格率为 80% ,你认为买哪一种产品更可靠?
(3)阿强在一次抽奖活动中,只抽了一张,就中了一等奖,能不能说这次抽奖活动的中奖率为百分之百?为什么?
(1) 从一副扑克牌(除去大小王)中任抽一张.
P (抽到红心) = ;
1
4
-
P (抽到黑桃) = ;
1
4
-
P (抽到红心3)= ;
1
-
52
1
-
13
P (抽到5)= .
(2)有5张数字卡片,它们的背面完全相同,正面分别标有1,2,2,3,4。现将它们的背面朝上,从中任意摸到一张卡片,则:
P(摸到1号卡片)=
1
-
5
p (摸到2号卡片)= ;
2
-
5
p (摸到3号卡片)= ;
1
-
5
p (摸到4号卡片)= ;
1
-
5
p (摸到奇数号卡片)= ;
2
-
5
P(摸到偶数号卡片) = .
3
-
5
(1)袋子里有1个红球,3个白球和5个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则
P(摸到红球)= ;
P(摸到白球)= ;
P(摸到黄球)= .
1
-
9
1
-
3
5
-
9
( 2 )任意翻一下2004年日历,
翻出1月6日的概率为 ;翻
出4月31日的概
率为 .
1/366
0
课堂小结:
1.预测随机事件在每一次实验中发生的可能性,可以预先估计随机事件在每一次实验中发生的机会有多大,不发生的机会机会有多大.
随机事件的发生与不发生的机会不总是对半的(都为50%),应通过开展一系列数学实践活动从中掌握预测的一些规律.
P
作业习题13.2
祝同学们
祝同学们
进步
进步
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
