1.5 利用三角形全等测距离 同步练习(含答案)
文档属性
| 名称 | 1.5 利用三角形全等测距离 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 08:42:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章 三角形
5 利用三角形全等测距离
知识能力全练
知识点 利用三角形全等测量两点间的距离
1.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
A.SSS B.SAS C.ASA D.AAS
2.如图所示,AD、BC表示两根长度相同的木条,若O是AD、BC的中点,经测量,AB=9cm,则容器的内径CD为_________cm.
3.如图所示,李飒为测量被一座小山隔开的A、B两点间的距离,设计了如下测量方案:在小山旁边取一点O,使点O能直接到达A、B两点,连接AO并延长到C,使AO=OC,连接BO并延长到D,使BO=OD,这时,只要测出线段________的长度就可知A、B两点间的距离,这是根据_________判定________≌_________.
4.如图所示,太阳光线AC与A'C'是平行的,同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗?说说你的理由.
巩固提高全练
5.如图所示,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上,可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.AAS C.SSS D.ASA
6.如图所示,王强同学用10块高度都是2 cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和点B分别与木墙的顶端重合,则两堵木墙之间的距离为________cm.
7.如图所示,某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时停止行走;
④测得DE的长为5米.
根据他们的做法,回答下列问题:
(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
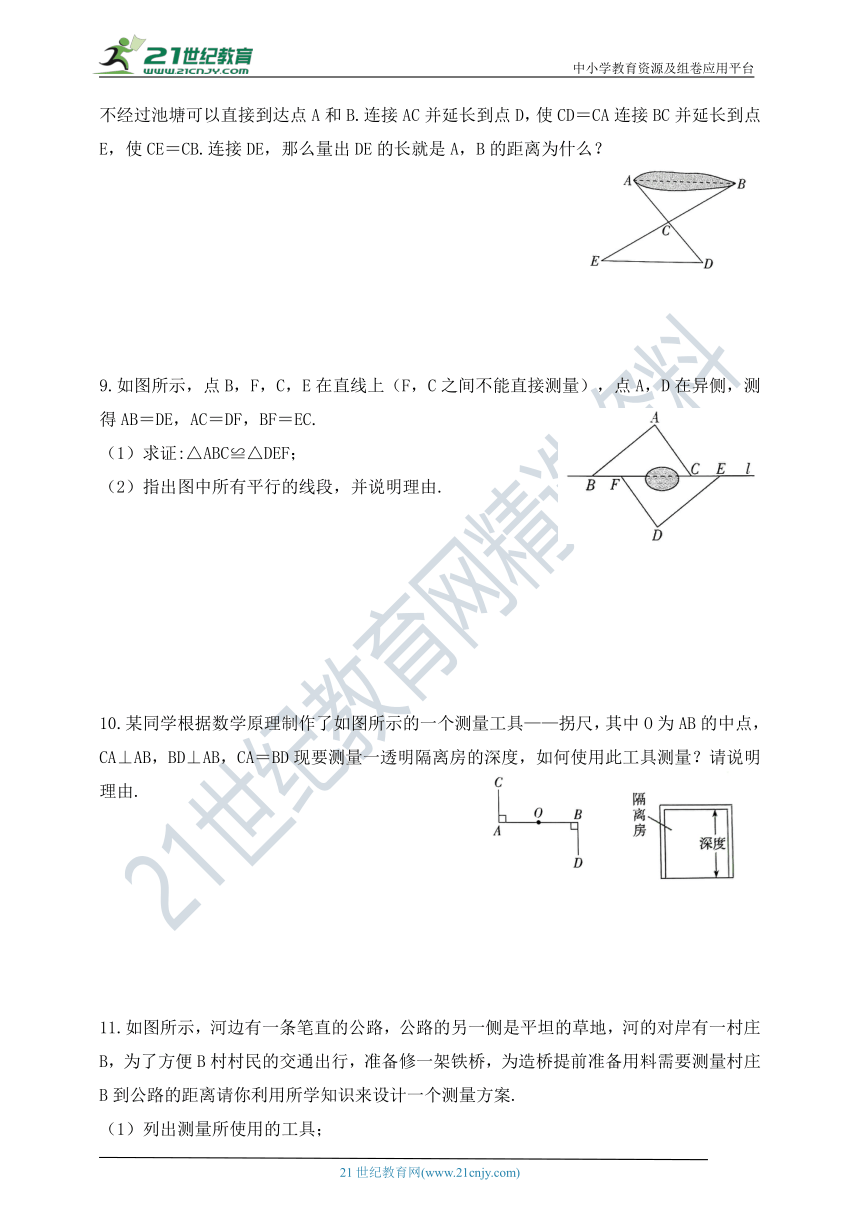
8.如图所示,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离为什么?
9.如图所示,点B,F,C,E在直线上(F,C之间不能直接测量),点A,D在异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
10.某同学根据数学原理制作了如图所示的一个测量工具——拐尺,其中O为AB的中点,CA⊥AB,BD⊥AB,CA=BD现要测量一透明隔离房的深度,如何使用此工具测量?请说明理由.
11.如图所示,河边有一条笔直的公路,公路的另一侧是平坦的草地,河的对岸有一村庄B,为了方便B村村民的交通出行,准备修一架铁桥,为造桥提前准备用料需要测量村庄B到公路的距离请你利用所学知识来设计一个测量方案.
(1)列出测量所使用的工具;
(2)画出测量的示意图,写出测量的步骤;
(3)用字母表示测量的数据,求村庄B与公路之间的距离.
参考答案
1.B 2.9 3.CD;SAS;△AOB;△COD
4.解析 影子一样长.
理由:∵AB⊥BC,A?B?⊥B?C?,∴∠ABC=∠A?B?C?=90°,
∵AC∥A?C?,∴∠ACB=∠A?C?B?.
在△ABC和△A?B?C?中,∴△ABC≌△A?B?C?(AAS),
∴BC=B?C?,即影子一样长.
5.D 6.20
7.解析(1)河宽AB是5米.
(2)由题意知,在△ABC和△EDC中,
∴△ABC≌△EDC(ASA),∴AB=ED.
故河宽AB就是测得的DE的长,因此他们的做法是正确的.
8.解析 理由如下:
在△ABC和△DEC中,∴△ABC≌△DEC(SAS),
∴AB=DE.故量出DE的长就是A,B的距离.
9.解析(1)证明:∵BF=CE,∴BF+FC=FC+CE,即BC=EF.
在△ABC和△DEF中,∴△ABC≌△DEF(SSS).
(2)AB∥DE,AC∥DF
理由:∵△ABC≌△DEF,∴∠ABC=∠DEF、∠ACB=∠DFE,∴AB∥DE,AC∥DF.
10.解析 如图所示,使AC与房间内壁在一条直线上,且C与一端点接触,然后人在BD的延长线上移动至F,使F、O、E三点正好在一条直线上,记下F点,这时量出DF的长即为房间深度CE的长.
理由:∵CA⊥AB,DB⊥AB,∴∠A=∠B=90°,
在△BOF和△AOE中,∴△BOF≌△AOE(ASA),
∴BF=AE(全等三角形的对应边相等).
∵AC=BD,∴AE=AC=BF-BD,即CE=DF.
11.解析 (1)所使用的工具为测角器、卷尺.
(2)测量的示意图如图所示,
测量步骤如下:
①在公路上取点A,C,用测角器测得∠BAC=90°;
②用测角器测得∠ACB=α;
③作射线CD,使∠ACD=α,且交BA的延长线于点D;
④用卷尺测出AD=m米.
(3)由作法可知,在△BAC和△DAC中,
∵∠BAC=∠DAC=90°,AC=AC,∠ACB=∠ACD,
△BAC≌△DAC(ASA).
∴AB=AD.因此点B与公路之间的距离为m米.
_21?????????è?????(www.21cnjy.com)_
第一章 三角形
5 利用三角形全等测距离
知识能力全练
知识点 利用三角形全等测量两点间的距离
1.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
A.SSS B.SAS C.ASA D.AAS
2.如图所示,AD、BC表示两根长度相同的木条,若O是AD、BC的中点,经测量,AB=9cm,则容器的内径CD为_________cm.
3.如图所示,李飒为测量被一座小山隔开的A、B两点间的距离,设计了如下测量方案:在小山旁边取一点O,使点O能直接到达A、B两点,连接AO并延长到C,使AO=OC,连接BO并延长到D,使BO=OD,这时,只要测出线段________的长度就可知A、B两点间的距离,这是根据_________判定________≌_________.
4.如图所示,太阳光线AC与A'C'是平行的,同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗?说说你的理由.
巩固提高全练
5.如图所示,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上,可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.AAS C.SSS D.ASA
6.如图所示,王强同学用10块高度都是2 cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和点B分别与木墙的顶端重合,则两堵木墙之间的距离为________cm.
7.如图所示,某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时停止行走;
④测得DE的长为5米.
根据他们的做法,回答下列问题:
(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
8.如图所示,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离为什么?
9.如图所示,点B,F,C,E在直线上(F,C之间不能直接测量),点A,D在异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
10.某同学根据数学原理制作了如图所示的一个测量工具——拐尺,其中O为AB的中点,CA⊥AB,BD⊥AB,CA=BD现要测量一透明隔离房的深度,如何使用此工具测量?请说明理由.
11.如图所示,河边有一条笔直的公路,公路的另一侧是平坦的草地,河的对岸有一村庄B,为了方便B村村民的交通出行,准备修一架铁桥,为造桥提前准备用料需要测量村庄B到公路的距离请你利用所学知识来设计一个测量方案.
(1)列出测量所使用的工具;
(2)画出测量的示意图,写出测量的步骤;
(3)用字母表示测量的数据,求村庄B与公路之间的距离.
参考答案
1.B 2.9 3.CD;SAS;△AOB;△COD
4.解析 影子一样长.
理由:∵AB⊥BC,A?B?⊥B?C?,∴∠ABC=∠A?B?C?=90°,
∵AC∥A?C?,∴∠ACB=∠A?C?B?.
在△ABC和△A?B?C?中,∴△ABC≌△A?B?C?(AAS),
∴BC=B?C?,即影子一样长.
5.D 6.20
7.解析(1)河宽AB是5米.
(2)由题意知,在△ABC和△EDC中,
∴△ABC≌△EDC(ASA),∴AB=ED.
故河宽AB就是测得的DE的长,因此他们的做法是正确的.
8.解析 理由如下:
在△ABC和△DEC中,∴△ABC≌△DEC(SAS),
∴AB=DE.故量出DE的长就是A,B的距离.
9.解析(1)证明:∵BF=CE,∴BF+FC=FC+CE,即BC=EF.
在△ABC和△DEF中,∴△ABC≌△DEF(SSS).
(2)AB∥DE,AC∥DF
理由:∵△ABC≌△DEF,∴∠ABC=∠DEF、∠ACB=∠DFE,∴AB∥DE,AC∥DF.
10.解析 如图所示,使AC与房间内壁在一条直线上,且C与一端点接触,然后人在BD的延长线上移动至F,使F、O、E三点正好在一条直线上,记下F点,这时量出DF的长即为房间深度CE的长.
理由:∵CA⊥AB,DB⊥AB,∴∠A=∠B=90°,
在△BOF和△AOE中,∴△BOF≌△AOE(ASA),
∴BF=AE(全等三角形的对应边相等).
∵AC=BD,∴AE=AC=BF-BD,即CE=DF.
11.解析 (1)所使用的工具为测角器、卷尺.
(2)测量的示意图如图所示,
测量步骤如下:
①在公路上取点A,C,用测角器测得∠BAC=90°;
②用测角器测得∠ACB=α;
③作射线CD,使∠ACD=α,且交BA的延长线于点D;
④用卷尺测出AD=m米.
(3)由作法可知,在△BAC和△DAC中,
∵∠BAC=∠DAC=90°,AC=AC,∠ACB=∠ACD,
△BAC≌△DAC(ASA).
∴AB=AD.因此点B与公路之间的距离为m米.
_21?????????è?????(www.21cnjy.com)_
