2012年中考第一轮复习精品教学案:九、四边形
文档属性
| 名称 | 2012年中考第一轮复习精品教学案:九、四边形 |

|
|
| 格式 | zip | ||
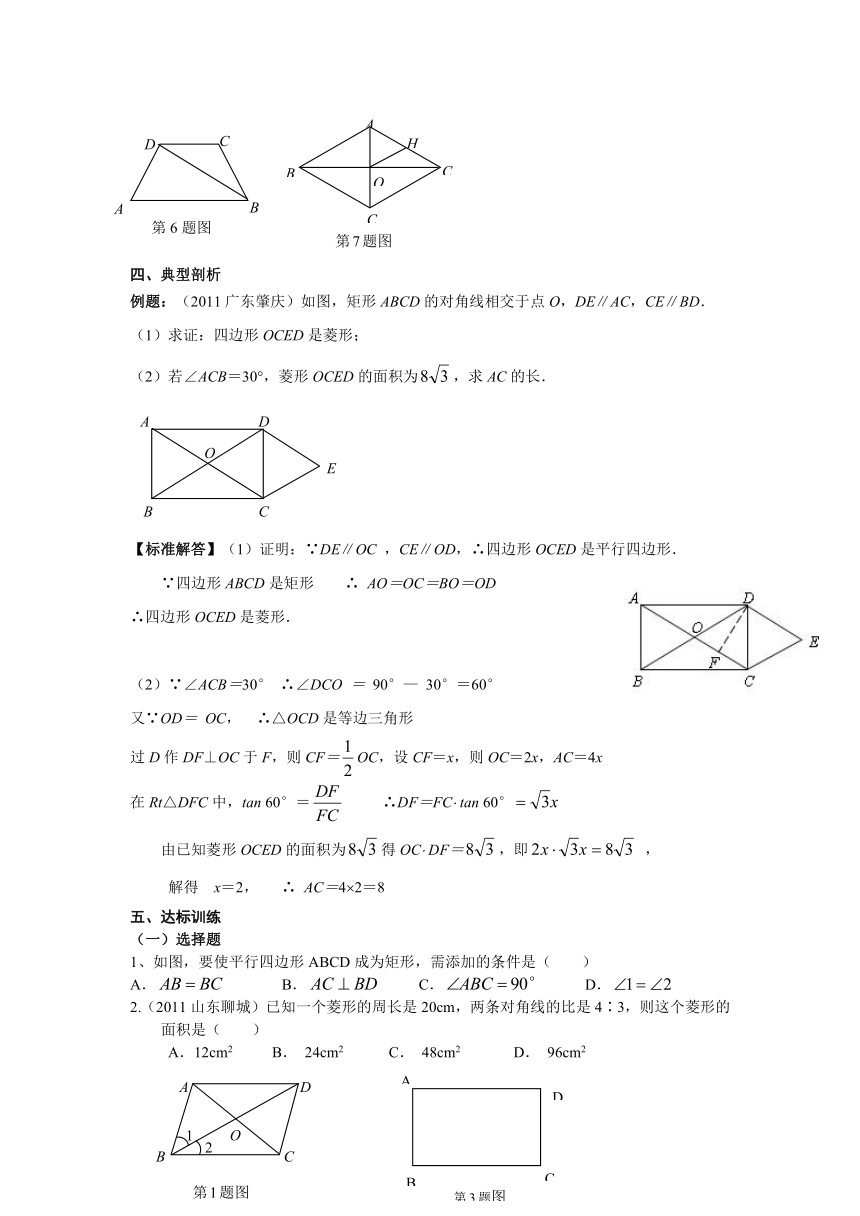
| 文件大小 | 141.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-15 00:00:00 | ||
图片预览

文档简介
九、四边形
一、学习目标
1.理解多边形,多边形的顶点、边、内角、外角及对角线等概念,理解多边形的内角和定理,掌握四边形的内角和和外角和都是360°的性质;
2.了解两点间的距离。点到直线的距离与两条平行线之间的距离及三者之间的联系,了解平行四边形不稳定性的应用,理解两条平行线间的距离概念;
3. 掌握平行四边形、矩形、菱形、正方形、等腰梯形等概念,掌握平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定以及梯形的中位线定理。
二、知识要点
四边形、四边形的内角和与外角和、多边形、多边形的内角和与外角和、平行四边形、平行四边形的性质和判定、两条平行线间的距离,矩形、菱形、正方形、梯形的性质和判定、梯形中位线定理。
三、考点再现
1.(2011广西来宾)如果一个多边形的内角和是其外角和的一半,那么这个多边形是( )
A.六边形 B.五边形 C.四边形 D.三角形
2. (2011江苏泰州)四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判定这个四边形是平行四边形的条件有
A.1组 B.2组 C.3组 D.4组
3. (2011辽宁沈阳)如图,矩形ABCD中,AB<BC,对角线AC、BD相交于点O,则图中的等腰三角形有( )
A.2个 B.4个 C. 6个 D.8个
4. (2011四川内江)如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足( )条件时,四边形EFGH是菱形.
A.AC=BD B.AC⊥BD C.四边形ABCD 是菱形 D.四边形ABCD 是梯形
5.(2011广西贵港)如图所示,在矩形ABCD中,AB=,BC=2,对角线AC、BD相交于点O,过点O作OE⊥AC交AD于点E,则AE的长是( )
A. B.C. 1 D.1.5
6. (2011湖北武汉市)如图,在梯形ABCD中,AB∥DC,AD=DC=CB,若∠ABD=25°,则∠BAD的大小是( )
A.40°. B.45°. C.50°. D.60°.
7.如图所示,菱形中,对角线相交于点,为边中点,菱形的周长为24,则的长等于( ).
A.1 B.2 C.3 D.4
四、典型剖析
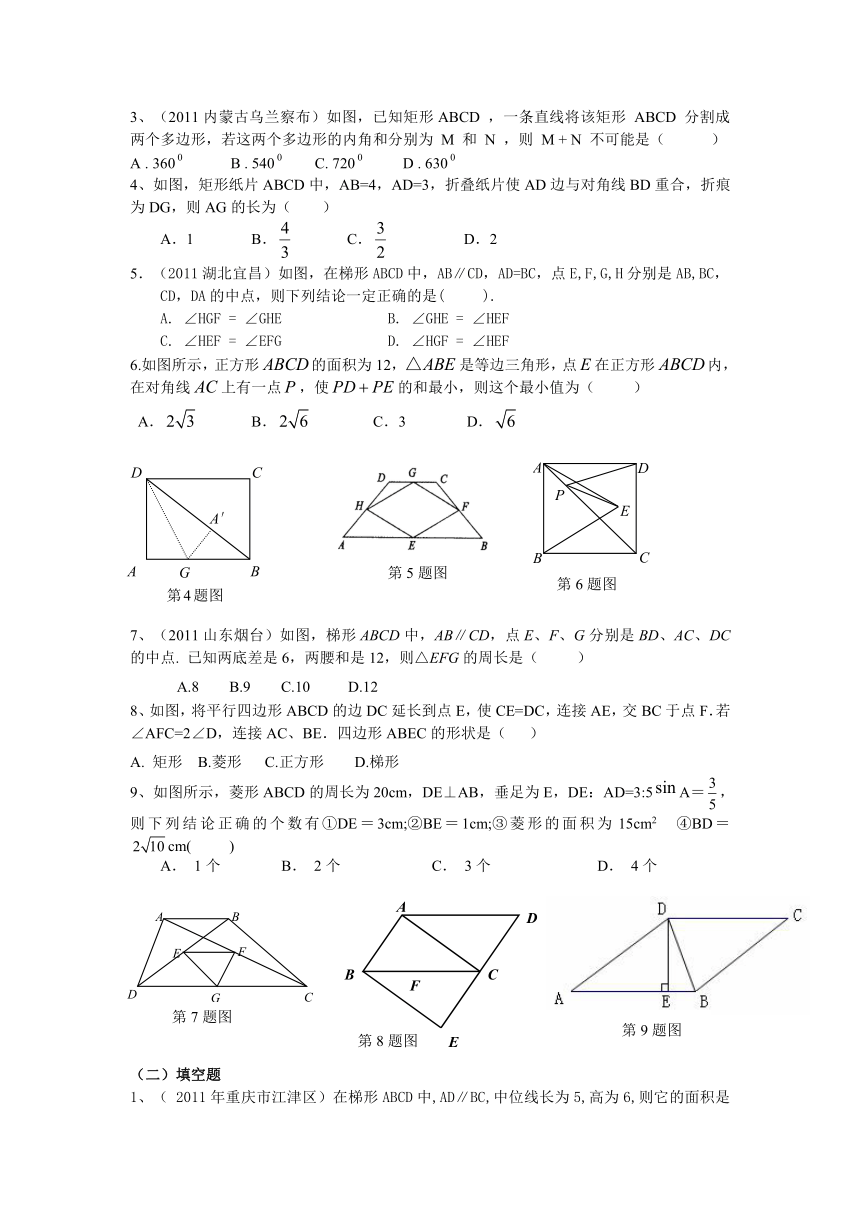
例题:(2011广东肇庆)如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30,菱形OCED的面积为,求AC的长.
【标准解答】(1)证明:∵DE∥OC ,CE∥OD,∴四边形OCED是平行四边形.
∵四边形ABCD是矩形 ∴ AO=OC=BO=OD
∴四边形OCED是菱形.
(2)∵∠ACB=30° ∴∠DCO = 90°— 30°=60°
又∵OD= OC, ∴△OCD是等边三角形
过D作DF⊥OC于F,则CF=OC,设CF=x,则OC=2x,AC=4x
在Rt△DFC中,tan 60°= ∴DF=FC tan 60°
由已知菱形OCED的面积为得OC DF=,即 ,
解得 x=2, ∴ AC=42=8
五、达标训练
(一)选择题
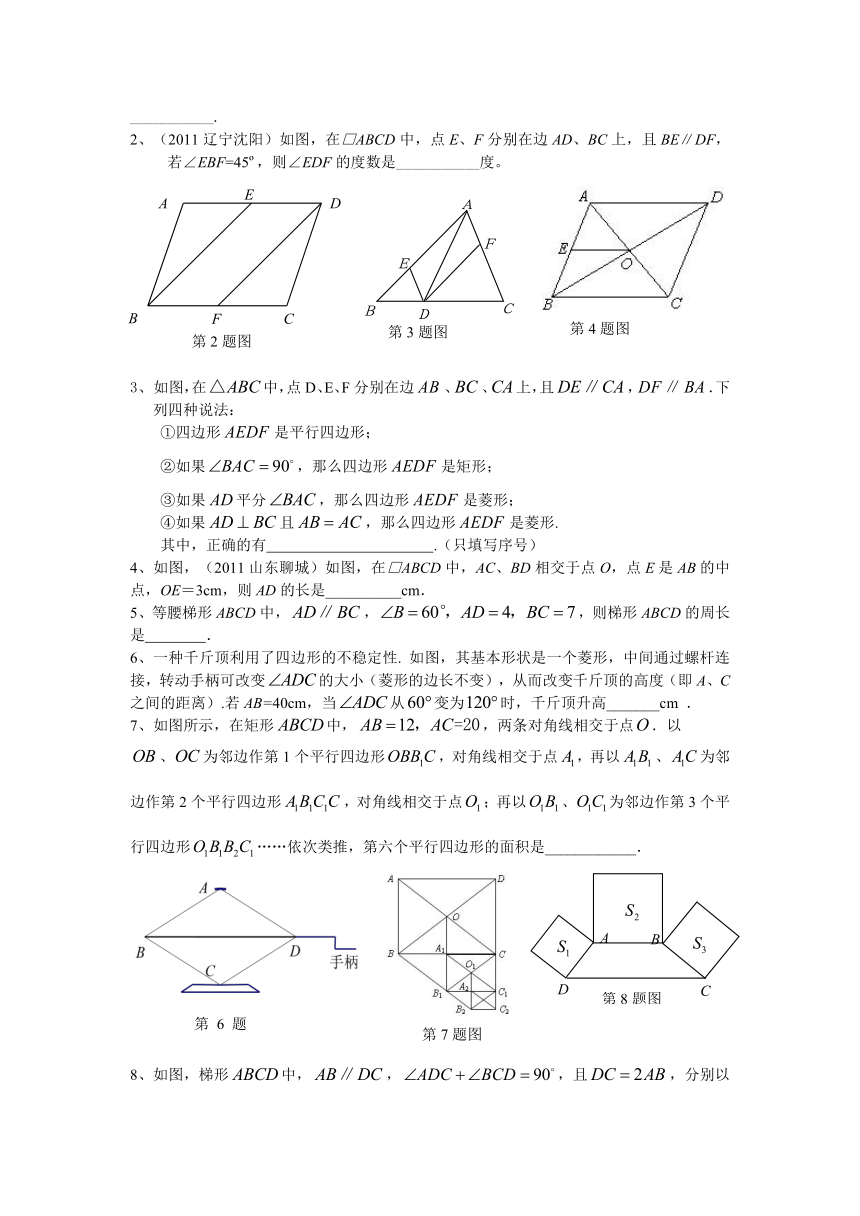
1、如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A. B. C. D.
2.(2011山东聊城)已知一个菱形的周长是20cm,两条对角线的比是4∶3,则这个菱形的面积是( )
A.12cm2 B. 24cm2 C. 48cm2 D. 96cm2
3、(2011内蒙古乌兰察布)如图,已知矩形ABCD ,一条直线将该矩形 ABCD 分割成两个多边形,若这两个多边形的内角和分别为 M 和 N ,则 M + N 不可能是( )
A . 360 B . 540 C. 720 D . 630
4、如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,则AG的长为( )
A.1 B. C. D.2
5.(2011湖北宜昌)如图,在梯形ABCD中,AB∥CD,AD=BC,点E,F,G,H分别是AB,BC,CD,DA的中点,则下列结论一定正确的是( ).
A. ∠HGF = ∠GHE B. ∠GHE = ∠HEF
C. ∠HEF = ∠EFG D. ∠HGF = ∠HEF
6.如图所示,正方形的面积为12,是等边三角形,点在正方形内,在对角线上有一点,使的和最小,则这个最小值为( )
A. B. C.3 D.
7、(2011山东烟台)如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点. 已知两底差是6,两腰和是12,则△EFG的周长是( )
A.8 B.9 C.10 D.12
8、如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.若∠AFC=2∠D,连接AC、BE.四边形ABEC的形状是( )
A. 矩形 B.菱形 C.正方形 D.梯形
9、如图所示,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,DE:AD=3:5A=,则下列结论正确的个数有①DE=3cm;②BE=1cm;③菱形的面积为15cm2 ④BD=cm( )
A. 1个 B. 2个 C. 3个 D. 4个
(二)填空题
1、( 2011年重庆市江津区)在梯形ABCD中,AD∥BC,中位线长为5,高为6,则它的面积是___________.
2、(2011辽宁沈阳)如图,在□ABCD中,点E、F分别在边AD、BC上,且BE∥DF,若∠EBF=45 ,则∠EDF的度数是___________度。
3、 如图,在中,点D、E、F分别在边、、上,且,.下列四种说法:
①四边形是平行四边形;
②如果,那么四边形是矩形;
③如果平分,那么四边形是菱形;
④如果且,那么四边形是菱形.
其中,正确的有 .(只填写序号)
4、如图,(2011山东聊城)如图,在□ABCD中,AC、BD相交于点O,点E是AB的中点,OE=3cm,则AD的长是__________cm.
5、等腰梯形ABCD中,,,则梯形ABCD的周长是 .
6、一种千斤顶利用了四边形的不稳定性. 如图,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变的大小(菱形的边长不变),从而改变千斤顶的高度(即A、C 之间的距离).若AB=40cm,当从变为时,千斤顶升高_______cm .
7、如图所示,在矩形中,,两条对角线相交于点.以
、为邻边作第1个平行四边形,对角线相交于点,再以、为邻边作第2个平行四边形,对角线相交于点;再以、为邻边作第3个平行四边形……依次类推,第六个平行四边形的面积是____________.
8、如图,梯形中,,,且,分别以为边向梯形外作正方形,其面积分别为,则之间的关系是 .
(三)解答题
1、(2011广东肇庆)如图,在正方形ABCD中,E为对角线AC上一点,连接EB、ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,若∠DEB = 140,求∠AFE的度数.
2、两个全等的直角三角形重叠放在直线上,如图⑴,AB=6cm,BC=8cm,∠ABC=90°,将Rt△ABC在直线上左右平移,如图⑵所示.
⑴ 四边形ACFD是平行四边形吗?说明理由;
⑵ 怎样移动Rt△ABC,使得四边形ACFD为菱形;
3、(2011山东滨州改编)如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF.
(1)那么当点O运动到何处时,四边形AECF是矩形?
(2) 当点O运动到何处时,且△ABC满足什么条件时,四边形AECF是菱形?
4、(2011山东泰安)已知,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC
(1)点F是DC上一点,连接EF,交AC于点O(如图①),求证:△AOE∽△COF
(2)若点F是DC的中点,连接BD,交AE于点G(如图②),求证:四边形EFDG是菱形。
六、学习感悟
九、四边形 参考答案:
考点再现:D 、C 、B、B、B、C、C.
达标训练:
一、选择 1、 C;2、B;3、D;4、C;5、D;6、A;7、B;8、A;9、C。
二、填空1、 30;2、45°;3、①②③④;4、6;5、17;6、;7、3;8、S22=S12+S32
三、解答题
1.解:(1)证明:∵四边形ABCD 是正方形 ∴CD=CB,
∵AC是正方形的对角线 ∴∠DCA=∠BCA
又 CE=CE ∴△BEC≌△DEC
(2)∵∠DEB=140
由△BEC≌△DEC可得∠DEC=∠BEC=1402=70,
∴∠AEF=∠BEC=70,
又∵AC是正方形的对角线, ∠DAB=90 ∴∠DAC=∠BAC=902=45,
在△AEF中,∠AFE=180— 70— 45=65
2. (1)是
因为△ABC≌△DEF,所以AC=DF,∠ACB=∠DFE,所以AC∥DF,所以四边形ACFD是平行四边形;
(2)在Rt△ABC中,由勾股定理得AC=10cm,要使四边形ACFD为菱形,则AC=CF,由勾股定理得出AC===10cm.所以可将Rt△ABC向左平移10cm或向右平移10cm;
3. 解:(1)当点O运动到AC的中点(或OA=OC)时,
四边形AECF是矩形.
因为CE平分∠BCA,所以∠1=∠2.
又因为MN∥BC,所以∠1=∠3.
所以∠3=∠2,所以EO=CO.
同理,FO=CO.
所以EO=FO.
又OA=OC,所以四边形AECF是平行四边形.
方法一:又因为∠1=∠2,∠4=∠5,
所以∠1+∠5=∠2+∠4.
又因为∠1+∠5+∠2+∠4=180°,
所以∠2+∠4=90°.
所以四边形AECF是矩形.
方法二:因为EO=CO,FO=CO,OA=OC,所以EO=CO=FO=OA,即AC=EF.
所以平行四边形AECF是矩形.
(2) 当点O运动到AC的中点(或OA=OC)且∠ACB=90°时,四边形AECF是菱形.
由(1)知,当点O运动到AC的中点(或OA=OC)时,四边形AECF是平行四边形.因为MN∥BC∠,ACB=90°,所以MN⊥AC,所以四边形AECF是四边形AECF是菱形.
4. 证明:(1)∵点E是BC的中点,BC=2AD,
∴EC=BE= BC=AD,
又∵AD∥EC,
∴四边形AECD为平行四边形,
∴AE∥DC,
∴∠AEO=∠CFO,∠EAO=∠FCO,
∴△AOE∽△COF;
(2)连接DE,
∵AD∥BE,AD=BE,
∴四边形ABED是平行四边形,
又∠ABE=90°,
∴四边形ABED是矩形,
∴GE=GA=GB=GD= BD= AE,
∴E、F分别是BC、CD的中点,
∴EF、GE是△CBD的两条中位线,
∴EF= BD=GD,GE= CD=DF,
又GE=GD,
∴EF=GD=GE=DF,
∴四边形EFDG是菱形.
(命题人:仪阳 司强、辛显顺、赵爱华、鹿向明、刘倩)
A
B
C
D
E
F
G 第4题 题题
H
BA
A
CA
DA
OA
第3题图
第5题
A
B
C
D
E
O
B
A
H
C
C
O
第7题图
第6题图
A
B
C
D
A
B
C
D
E
O
A
C
B
D
第3题图
1
2
B
C
D
A
O
第1题图
A
D
E
P
B
C
第6题图
第5题图
A′
G
D
B
C
A
第4题图
A
B
C
D
E
F
第8题图
第9题图
A
B
C
D
E
F
G
第7题图
第4题图
A
F
C
D
B
E
第3题图
A
BA
CA
DA
EA
FA
第2题图
第7题图
A
B
D
C
第8题图
第6题图
1题图
3题图
一、学习目标
1.理解多边形,多边形的顶点、边、内角、外角及对角线等概念,理解多边形的内角和定理,掌握四边形的内角和和外角和都是360°的性质;
2.了解两点间的距离。点到直线的距离与两条平行线之间的距离及三者之间的联系,了解平行四边形不稳定性的应用,理解两条平行线间的距离概念;
3. 掌握平行四边形、矩形、菱形、正方形、等腰梯形等概念,掌握平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定以及梯形的中位线定理。
二、知识要点
四边形、四边形的内角和与外角和、多边形、多边形的内角和与外角和、平行四边形、平行四边形的性质和判定、两条平行线间的距离,矩形、菱形、正方形、梯形的性质和判定、梯形中位线定理。
三、考点再现
1.(2011广西来宾)如果一个多边形的内角和是其外角和的一半,那么这个多边形是( )
A.六边形 B.五边形 C.四边形 D.三角形
2. (2011江苏泰州)四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判定这个四边形是平行四边形的条件有
A.1组 B.2组 C.3组 D.4组
3. (2011辽宁沈阳)如图,矩形ABCD中,AB<BC,对角线AC、BD相交于点O,则图中的等腰三角形有( )
A.2个 B.4个 C. 6个 D.8个
4. (2011四川内江)如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足( )条件时,四边形EFGH是菱形.
A.AC=BD B.AC⊥BD C.四边形ABCD 是菱形 D.四边形ABCD 是梯形
5.(2011广西贵港)如图所示,在矩形ABCD中,AB=,BC=2,对角线AC、BD相交于点O,过点O作OE⊥AC交AD于点E,则AE的长是( )
A. B.C. 1 D.1.5
6. (2011湖北武汉市)如图,在梯形ABCD中,AB∥DC,AD=DC=CB,若∠ABD=25°,则∠BAD的大小是( )
A.40°. B.45°. C.50°. D.60°.
7.如图所示,菱形中,对角线相交于点,为边中点,菱形的周长为24,则的长等于( ).
A.1 B.2 C.3 D.4
四、典型剖析
例题:(2011广东肇庆)如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30,菱形OCED的面积为,求AC的长.
【标准解答】(1)证明:∵DE∥OC ,CE∥OD,∴四边形OCED是平行四边形.
∵四边形ABCD是矩形 ∴ AO=OC=BO=OD
∴四边形OCED是菱形.
(2)∵∠ACB=30° ∴∠DCO = 90°— 30°=60°
又∵OD= OC, ∴△OCD是等边三角形
过D作DF⊥OC于F,则CF=OC,设CF=x,则OC=2x,AC=4x
在Rt△DFC中,tan 60°= ∴DF=FC tan 60°
由已知菱形OCED的面积为得OC DF=,即 ,
解得 x=2, ∴ AC=42=8
五、达标训练
(一)选择题
1、如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A. B. C. D.
2.(2011山东聊城)已知一个菱形的周长是20cm,两条对角线的比是4∶3,则这个菱形的面积是( )
A.12cm2 B. 24cm2 C. 48cm2 D. 96cm2
3、(2011内蒙古乌兰察布)如图,已知矩形ABCD ,一条直线将该矩形 ABCD 分割成两个多边形,若这两个多边形的内角和分别为 M 和 N ,则 M + N 不可能是( )
A . 360 B . 540 C. 720 D . 630
4、如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,则AG的长为( )
A.1 B. C. D.2
5.(2011湖北宜昌)如图,在梯形ABCD中,AB∥CD,AD=BC,点E,F,G,H分别是AB,BC,CD,DA的中点,则下列结论一定正确的是( ).
A. ∠HGF = ∠GHE B. ∠GHE = ∠HEF
C. ∠HEF = ∠EFG D. ∠HGF = ∠HEF
6.如图所示,正方形的面积为12,是等边三角形,点在正方形内,在对角线上有一点,使的和最小,则这个最小值为( )
A. B. C.3 D.
7、(2011山东烟台)如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点. 已知两底差是6,两腰和是12,则△EFG的周长是( )
A.8 B.9 C.10 D.12
8、如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.若∠AFC=2∠D,连接AC、BE.四边形ABEC的形状是( )
A. 矩形 B.菱形 C.正方形 D.梯形
9、如图所示,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,DE:AD=3:5A=,则下列结论正确的个数有①DE=3cm;②BE=1cm;③菱形的面积为15cm2 ④BD=cm( )
A. 1个 B. 2个 C. 3个 D. 4个
(二)填空题
1、( 2011年重庆市江津区)在梯形ABCD中,AD∥BC,中位线长为5,高为6,则它的面积是___________.
2、(2011辽宁沈阳)如图,在□ABCD中,点E、F分别在边AD、BC上,且BE∥DF,若∠EBF=45 ,则∠EDF的度数是___________度。
3、 如图,在中,点D、E、F分别在边、、上,且,.下列四种说法:
①四边形是平行四边形;
②如果,那么四边形是矩形;
③如果平分,那么四边形是菱形;
④如果且,那么四边形是菱形.
其中,正确的有 .(只填写序号)
4、如图,(2011山东聊城)如图,在□ABCD中,AC、BD相交于点O,点E是AB的中点,OE=3cm,则AD的长是__________cm.
5、等腰梯形ABCD中,,,则梯形ABCD的周长是 .
6、一种千斤顶利用了四边形的不稳定性. 如图,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变的大小(菱形的边长不变),从而改变千斤顶的高度(即A、C 之间的距离).若AB=40cm,当从变为时,千斤顶升高_______cm .
7、如图所示,在矩形中,,两条对角线相交于点.以
、为邻边作第1个平行四边形,对角线相交于点,再以、为邻边作第2个平行四边形,对角线相交于点;再以、为邻边作第3个平行四边形……依次类推,第六个平行四边形的面积是____________.
8、如图,梯形中,,,且,分别以为边向梯形外作正方形,其面积分别为,则之间的关系是 .
(三)解答题
1、(2011广东肇庆)如图,在正方形ABCD中,E为对角线AC上一点,连接EB、ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,若∠DEB = 140,求∠AFE的度数.
2、两个全等的直角三角形重叠放在直线上,如图⑴,AB=6cm,BC=8cm,∠ABC=90°,将Rt△ABC在直线上左右平移,如图⑵所示.
⑴ 四边形ACFD是平行四边形吗?说明理由;
⑵ 怎样移动Rt△ABC,使得四边形ACFD为菱形;
3、(2011山东滨州改编)如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF.
(1)那么当点O运动到何处时,四边形AECF是矩形?
(2) 当点O运动到何处时,且△ABC满足什么条件时,四边形AECF是菱形?
4、(2011山东泰安)已知,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC
(1)点F是DC上一点,连接EF,交AC于点O(如图①),求证:△AOE∽△COF
(2)若点F是DC的中点,连接BD,交AE于点G(如图②),求证:四边形EFDG是菱形。
六、学习感悟
九、四边形 参考答案:
考点再现:D 、C 、B、B、B、C、C.
达标训练:
一、选择 1、 C;2、B;3、D;4、C;5、D;6、A;7、B;8、A;9、C。
二、填空1、 30;2、45°;3、①②③④;4、6;5、17;6、;7、3;8、S22=S12+S32
三、解答题
1.解:(1)证明:∵四边形ABCD 是正方形 ∴CD=CB,
∵AC是正方形的对角线 ∴∠DCA=∠BCA
又 CE=CE ∴△BEC≌△DEC
(2)∵∠DEB=140
由△BEC≌△DEC可得∠DEC=∠BEC=1402=70,
∴∠AEF=∠BEC=70,
又∵AC是正方形的对角线, ∠DAB=90 ∴∠DAC=∠BAC=902=45,
在△AEF中,∠AFE=180— 70— 45=65
2. (1)是
因为△ABC≌△DEF,所以AC=DF,∠ACB=∠DFE,所以AC∥DF,所以四边形ACFD是平行四边形;
(2)在Rt△ABC中,由勾股定理得AC=10cm,要使四边形ACFD为菱形,则AC=CF,由勾股定理得出AC===10cm.所以可将Rt△ABC向左平移10cm或向右平移10cm;
3. 解:(1)当点O运动到AC的中点(或OA=OC)时,
四边形AECF是矩形.
因为CE平分∠BCA,所以∠1=∠2.
又因为MN∥BC,所以∠1=∠3.
所以∠3=∠2,所以EO=CO.
同理,FO=CO.
所以EO=FO.
又OA=OC,所以四边形AECF是平行四边形.
方法一:又因为∠1=∠2,∠4=∠5,
所以∠1+∠5=∠2+∠4.
又因为∠1+∠5+∠2+∠4=180°,
所以∠2+∠4=90°.
所以四边形AECF是矩形.
方法二:因为EO=CO,FO=CO,OA=OC,所以EO=CO=FO=OA,即AC=EF.
所以平行四边形AECF是矩形.
(2) 当点O运动到AC的中点(或OA=OC)且∠ACB=90°时,四边形AECF是菱形.
由(1)知,当点O运动到AC的中点(或OA=OC)时,四边形AECF是平行四边形.因为MN∥BC∠,ACB=90°,所以MN⊥AC,所以四边形AECF是四边形AECF是菱形.
4. 证明:(1)∵点E是BC的中点,BC=2AD,
∴EC=BE= BC=AD,
又∵AD∥EC,
∴四边形AECD为平行四边形,
∴AE∥DC,
∴∠AEO=∠CFO,∠EAO=∠FCO,
∴△AOE∽△COF;
(2)连接DE,
∵AD∥BE,AD=BE,
∴四边形ABED是平行四边形,
又∠ABE=90°,
∴四边形ABED是矩形,
∴GE=GA=GB=GD= BD= AE,
∴E、F分别是BC、CD的中点,
∴EF、GE是△CBD的两条中位线,
∴EF= BD=GD,GE= CD=DF,
又GE=GD,
∴EF=GD=GE=DF,
∴四边形EFDG是菱形.
(命题人:仪阳 司强、辛显顺、赵爱华、鹿向明、刘倩)
A
B
C
D
E
F
G 第4题 题题
H
BA
A
CA
DA
OA
第3题图
第5题
A
B
C
D
E
O
B
A
H
C
C
O
第7题图
第6题图
A
B
C
D
A
B
C
D
E
O
A
C
B
D
第3题图
1
2
B
C
D
A
O
第1题图
A
D
E
P
B
C
第6题图
第5题图
A′
G
D
B
C
A
第4题图
A
B
C
D
E
F
第8题图
第9题图
A
B
C
D
E
F
G
第7题图
第4题图
A
F
C
D
B
E
第3题图
A
BA
CA
DA
EA
FA
第2题图
第7题图
A
B
D
C
第8题图
第6题图
1题图
3题图
同课章节目录
