2012年中考第一轮复习精品教学案:十一、解直角三角形
文档属性
| 名称 | 2012年中考第一轮复习精品教学案:十一、解直角三角形 |
|
|
| 格式 | zip | ||
| 文件大小 | 275.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-15 00:00:00 | ||
图片预览


文档简介
十一、解直角三角形
一、学习目标
1、能说出锐角三角函数的概念及特殊角的三角函数值,会运用三角函数进行有关计算.
2、会建构直角三角形模型,灵活运用锐角三角函数解决有关的实际问题.
二、知识要点
1、锐角三角函数的定义 2、特殊角的三角函数值 3、坡度、坡角的概念 4仰角、俯角的概念 5、解直角三角形的应用
三、考点再现
1、在中,∠C=90°,,,则下列结论正确的是( )
A. B. C. D.
2、在△ABC中,已知∠C=90°,sinB=,则cosA的值是( )
A. B. C. D.
3、计算: =
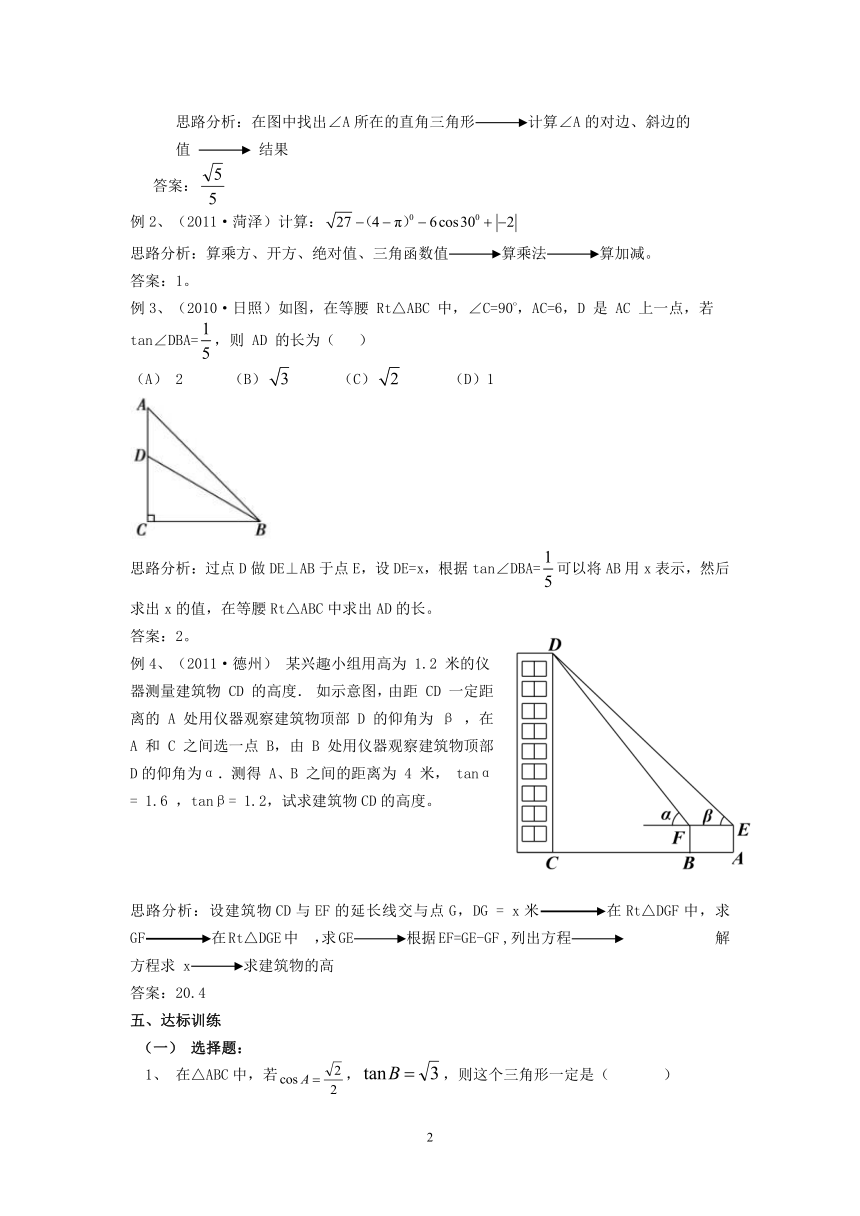
4、如图,已知在Rt△ABC中,∠C=90°,AC=1,则BD=
. 5、如图5,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m.如果在坡度为0.75的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为( )
A.5m B.6m C.7m D.8m
四、典例剖析
例1、(2011·连云港)△ABC的顶点都在方格纸的格点上,则sinA= .
思路分析:在图中找出∠A所在的直角三角形计算∠A的对边、斜边的
值 结果
答案:
例2、(2011·菏泽)计算:
思路分析:算乘方、开方、绝对值、三角函数值算乘法算加减。
答案:1。
例3、(2010·日照)如图,在等腰 Rt△ABC 中,∠C=90o,AC=6,D 是 AC 上一点,若 tan∠DBA=,则 AD 的长为( )
(A) 2 (B) (C) (D)1
思路分析:过点D做DE⊥AB于点E,设DE=x,根据tan∠DBA=可以将AB用x表示,然后求出x的值,在等腰Rt△ABC中求出AD的长。
答案:2。
例4、(2011·德州) 某兴趣小组用高为 1.2 米的仪器测量建筑物 CD 的高度. 如示意图,由距 CD 一定距离的 A 处用仪器观察建筑物顶部 D 的仰角为 β ,在 A 和 C 之间选一点 B,由 B 处用仪器观察建筑物顶部 D的仰角为α.测得 A、B 之间的距离为 4 米, tanα = 1.6 ,tanβ= 1.2,试求建筑物CD的高度。
思路分析:设建筑物CD与EF的延长线交与点G,DG = x米在Rt△DGF中,求GF在Rt△DGE中 ,求GE根据EF=GE-GF ,列出方程 解方程求 x求建筑物的高
答案:20.4
五、达标训练
(一) 选择题:
1、 在△ABC中,若,,则这个三角形一定是( )
(A)锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D)等腰三角形
2、在⊿ABC中,若各边的长度同时都扩大2倍,则锐角A的正弦值与余弦值的
情况( )
(A)都扩大2倍 (B)都缩小2倍 (C) 都不变 (D) 不确定
3、如图,铁路路基横断面为一个等腰梯形,若腰的坡度为i=
2∶3,顶宽是3米,路基高是4米,则路基的下底宽是( )
(A) 7米 (B)9米 (C)12米 (D) 15米
4、 如图,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阻影部分)的面积为( )
A. B. C. D. 1
5、(2011·菏泽)如图所示,已知在三角形纸片 ABC 中,BC=3, AB = 6 ,∠BCA=90°在 AC 上取一点 E ,以 BE为折痕, 使 AB 的一部分与 BC 重合,A 与BC 延长线上的点 D 重合,则 DE的长度为 ( ).
A.6 B.3 C. D.
6、(2011·日照)在 Rt△ABC 中,∠C=90°,把∠A 的邻边与对边的比叫做∠A 的余切,记作 cotA= .则下列关系式中不成立的是( )
(A)tanA·cotA=1 (B)sinA=tanA·cosA )
(C)cosA=cotA·sinA (D)tan2A+cot2A=1
7、如图,小强和小明去测量一座古塔的高度,他们在离古塔60米的A处,用测角仪器得塔顶的仰角为30°,已知测角仪器高AD=1.5米,则古塔BE的高为( )
(A)()米 (B)()米
(C) 米 (D) 米
(二) 填空题:
1、 若一个等腰三角形的两边长分别为2cm和6cm,则底边上的高为__________cm,
底角的余弦值为__________.
2、酒店在装修时,在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯宽2米,坡角为300,其侧面如图所示,则购买地毯至少需要__________元.(精确到0.1)
3、(2011·襄阳)在 207 国道襄阳段改造工程中,需沿 AC 方向开山修路(如图所示), 为了加快施工进度, 需要在小山的另一边同时施工。从AC上的一点 B 取∠ABD=140°,BD=1000m,∠D=50°.为了使开挖点 E 在直线 AC 上.那么 DE≈_______________m。(供选用的三角函数值: sin50°≈0.7660,cos50°≈0.6428,tan50°≈1.192)
4、(2009泸州)如图,已知Rt△ABC中,AC=3,BC= 4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,,…,则CA1=
5、如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为________米.(结果保留根号)
6、小明同学在东西方向的沿江大道A处,测得江中灯塔P在北偏东60°方向上,在A处正东400米的B处,测得江中灯塔P在北偏东30°方向上,则灯塔P到沿江大道的距离为____________米。
(三)解答题
1、特殊角的三角函数的有关计算
(1)(2009荆门)
(2)
2.如图,要在木里县某林场东西方向的两地之间修一条公路,已知点周围200米范围内为原始森林保护区,在上的点处测得在的北偏东45°方向上,从A向东走600米到达处,测得在点的北偏西60°方向上.
(1)是否穿过原始森林保护区?为什么?(参考数据:)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
3、某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西300,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)
4、(2011·潍坊)今年“五一”假期,某数学活动小组组织一次登山活动。他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达C点,路线如图所示。斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为300 ,已知A点海拔121米,C点海拔721米。
(1)求B点的海拔
(2)求斜坡AB的坡度
六、学习感悟
(实验中学 吴昌杰)
十一、解直角三角形 参考答案
考点再现 1、D 2、C 3、 4、 5、5m
典例剖析 1、 2、1 3、A 4、 20.4
达标训练
选择 1、A 2、C 3、D 4、A 5、C 6、D 7、B
填空 1、 2、426.2 3、 642.8 4、 5、 6 、 7、20
解答1、(1) (2) 2、不会 25天 3、30+10 4、(1)521米 (2)1:2.4
4题图
5题图
A
A
C
BB
例1
3题图
4题图
5题图
7题图
6题图
第2题
第5题
第3题
C
B
N
M
A
(第2题)
C
A
B
M
2
一、学习目标
1、能说出锐角三角函数的概念及特殊角的三角函数值,会运用三角函数进行有关计算.
2、会建构直角三角形模型,灵活运用锐角三角函数解决有关的实际问题.
二、知识要点
1、锐角三角函数的定义 2、特殊角的三角函数值 3、坡度、坡角的概念 4仰角、俯角的概念 5、解直角三角形的应用
三、考点再现
1、在中,∠C=90°,,,则下列结论正确的是( )
A. B. C. D.
2、在△ABC中,已知∠C=90°,sinB=,则cosA的值是( )
A. B. C. D.
3、计算: =
4、如图,已知在Rt△ABC中,∠C=90°,AC=1,则BD=
. 5、如图5,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m.如果在坡度为0.75的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为( )
A.5m B.6m C.7m D.8m
四、典例剖析
例1、(2011·连云港)△ABC的顶点都在方格纸的格点上,则sinA= .
思路分析:在图中找出∠A所在的直角三角形计算∠A的对边、斜边的
值 结果
答案:
例2、(2011·菏泽)计算:
思路分析:算乘方、开方、绝对值、三角函数值算乘法算加减。
答案:1。
例3、(2010·日照)如图,在等腰 Rt△ABC 中,∠C=90o,AC=6,D 是 AC 上一点,若 tan∠DBA=,则 AD 的长为( )
(A) 2 (B) (C) (D)1
思路分析:过点D做DE⊥AB于点E,设DE=x,根据tan∠DBA=可以将AB用x表示,然后求出x的值,在等腰Rt△ABC中求出AD的长。
答案:2。
例4、(2011·德州) 某兴趣小组用高为 1.2 米的仪器测量建筑物 CD 的高度. 如示意图,由距 CD 一定距离的 A 处用仪器观察建筑物顶部 D 的仰角为 β ,在 A 和 C 之间选一点 B,由 B 处用仪器观察建筑物顶部 D的仰角为α.测得 A、B 之间的距离为 4 米, tanα = 1.6 ,tanβ= 1.2,试求建筑物CD的高度。
思路分析:设建筑物CD与EF的延长线交与点G,DG = x米在Rt△DGF中,求GF在Rt△DGE中 ,求GE根据EF=GE-GF ,列出方程 解方程求 x求建筑物的高
答案:20.4
五、达标训练
(一) 选择题:
1、 在△ABC中,若,,则这个三角形一定是( )
(A)锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D)等腰三角形
2、在⊿ABC中,若各边的长度同时都扩大2倍,则锐角A的正弦值与余弦值的
情况( )
(A)都扩大2倍 (B)都缩小2倍 (C) 都不变 (D) 不确定
3、如图,铁路路基横断面为一个等腰梯形,若腰的坡度为i=
2∶3,顶宽是3米,路基高是4米,则路基的下底宽是( )
(A) 7米 (B)9米 (C)12米 (D) 15米
4、 如图,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阻影部分)的面积为( )
A. B. C. D. 1
5、(2011·菏泽)如图所示,已知在三角形纸片 ABC 中,BC=3, AB = 6 ,∠BCA=90°在 AC 上取一点 E ,以 BE为折痕, 使 AB 的一部分与 BC 重合,A 与BC 延长线上的点 D 重合,则 DE的长度为 ( ).
A.6 B.3 C. D.
6、(2011·日照)在 Rt△ABC 中,∠C=90°,把∠A 的邻边与对边的比叫做∠A 的余切,记作 cotA= .则下列关系式中不成立的是( )
(A)tanA·cotA=1 (B)sinA=tanA·cosA )
(C)cosA=cotA·sinA (D)tan2A+cot2A=1
7、如图,小强和小明去测量一座古塔的高度,他们在离古塔60米的A处,用测角仪器得塔顶的仰角为30°,已知测角仪器高AD=1.5米,则古塔BE的高为( )
(A)()米 (B)()米
(C) 米 (D) 米
(二) 填空题:
1、 若一个等腰三角形的两边长分别为2cm和6cm,则底边上的高为__________cm,
底角的余弦值为__________.
2、酒店在装修时,在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯宽2米,坡角为300,其侧面如图所示,则购买地毯至少需要__________元.(精确到0.1)
3、(2011·襄阳)在 207 国道襄阳段改造工程中,需沿 AC 方向开山修路(如图所示), 为了加快施工进度, 需要在小山的另一边同时施工。从AC上的一点 B 取∠ABD=140°,BD=1000m,∠D=50°.为了使开挖点 E 在直线 AC 上.那么 DE≈_______________m。(供选用的三角函数值: sin50°≈0.7660,cos50°≈0.6428,tan50°≈1.192)
4、(2009泸州)如图,已知Rt△ABC中,AC=3,BC= 4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,,…,则CA1=
5、如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上的影子约为10米,则大树的高约为________米.(结果保留根号)
6、小明同学在东西方向的沿江大道A处,测得江中灯塔P在北偏东60°方向上,在A处正东400米的B处,测得江中灯塔P在北偏东30°方向上,则灯塔P到沿江大道的距离为____________米。
(三)解答题
1、特殊角的三角函数的有关计算
(1)(2009荆门)
(2)
2.如图,要在木里县某林场东西方向的两地之间修一条公路,已知点周围200米范围内为原始森林保护区,在上的点处测得在的北偏东45°方向上,从A向东走600米到达处,测得在点的北偏西60°方向上.
(1)是否穿过原始森林保护区?为什么?(参考数据:)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
3、某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西300,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)
4、(2011·潍坊)今年“五一”假期,某数学活动小组组织一次登山活动。他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达C点,路线如图所示。斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为300 ,已知A点海拔121米,C点海拔721米。
(1)求B点的海拔
(2)求斜坡AB的坡度
六、学习感悟
(实验中学 吴昌杰)
十一、解直角三角形 参考答案
考点再现 1、D 2、C 3、 4、 5、5m
典例剖析 1、 2、1 3、A 4、 20.4
达标训练
选择 1、A 2、C 3、D 4、A 5、C 6、D 7、B
填空 1、 2、426.2 3、 642.8 4、 5、 6 、 7、20
解答1、(1) (2) 2、不会 25天 3、30+10 4、(1)521米 (2)1:2.4
4题图
5题图
A
A
C
BB
例1
3题图
4题图
5题图
7题图
6题图
第2题
第5题
第3题
C
B
N
M
A
(第2题)
C
A
B
M
2
同课章节目录
