2012年中考第一轮复习精品教学案:六、统计与概率
文档属性
| 名称 | 2012年中考第一轮复习精品教学案:六、统计与概率 |  | |
| 格式 | zip | ||
| 文件大小 | 256.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-15 22:48:50 | ||
图片预览



文档简介
统计与概率
一、考点梳理:
平均数、众数、中位数的概念、统计图的应用、统计知识的综合利用(包括方差、频数、频率等概念)、.事件分类(包括、确定事件、必然事件、不可能事件)、概率的计算、公平性问题等。
二、考点在线:
1.(2011山东泰安,9 ,3分)某校篮球班21名同学的身高如下表:
身高(cm) 180 186 188 192 208
人数(个) 4 6 5 4 2
则该校篮球班21名同学身高的众数和中位数分别是(单位:cm)( )
A.186,186 B.186,187 C.186,188 D.208,188
2(2011广东湛江9,3分)甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均数都是环,方差分别是,, ,则射箭成绩最稳定的是
A甲 B乙 C丙 D丁
3.(2011福建福州,8,4分)从1,2,-3三个数中,随机抽取两个数相乘,积是正数的概率是( )
A.0 B. C. D. 1
4.(2011广东株洲,4,3分)株洲市关心下一代工作委员会为了了解全市初三学生的视力状况,从全市30000名初三学生中随机抽取了500人进行视力测试,发现其中视力不良的学生有100人,则可估计全市30000名初三学生中视力不良的约有( )
A.100人 B.500人 C.6000人 D.15000 人
5.(2011四川成都,22,4分)某校在“爱护地球 绿化祖图”的创建活动中,组织学生开展植树造林活动.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
植树数量(单位:棵) 4 5 6 8 10
人数 30 22 25 15 8
则这100名同学平均每人植树 __________棵;若该校共有1000名学生,请根据以上调查结果估计该校学生的植树总数是__________棵.
6. (2011四川内江,13,5分)“Welcome to Senior High School.”(欢迎进入高中),在这段句子的所有英文字母中,字母o出现的频率是 .
三、精典剖析:
例1:(2011山东菏泽,19,10分)初中生对待学习的态度一直是教育工作者关注的问题之一.为此菏泽市教育局对我市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
(1)200;
(2)200-120-50=30(人).画图正确.
(3)C所占圆心角度数=360°×(1-25%-60%)=54°.
(4)12000×(25%+60%)=10200.
∴估计该市初中生中大约有10200名学生学习态度达标.
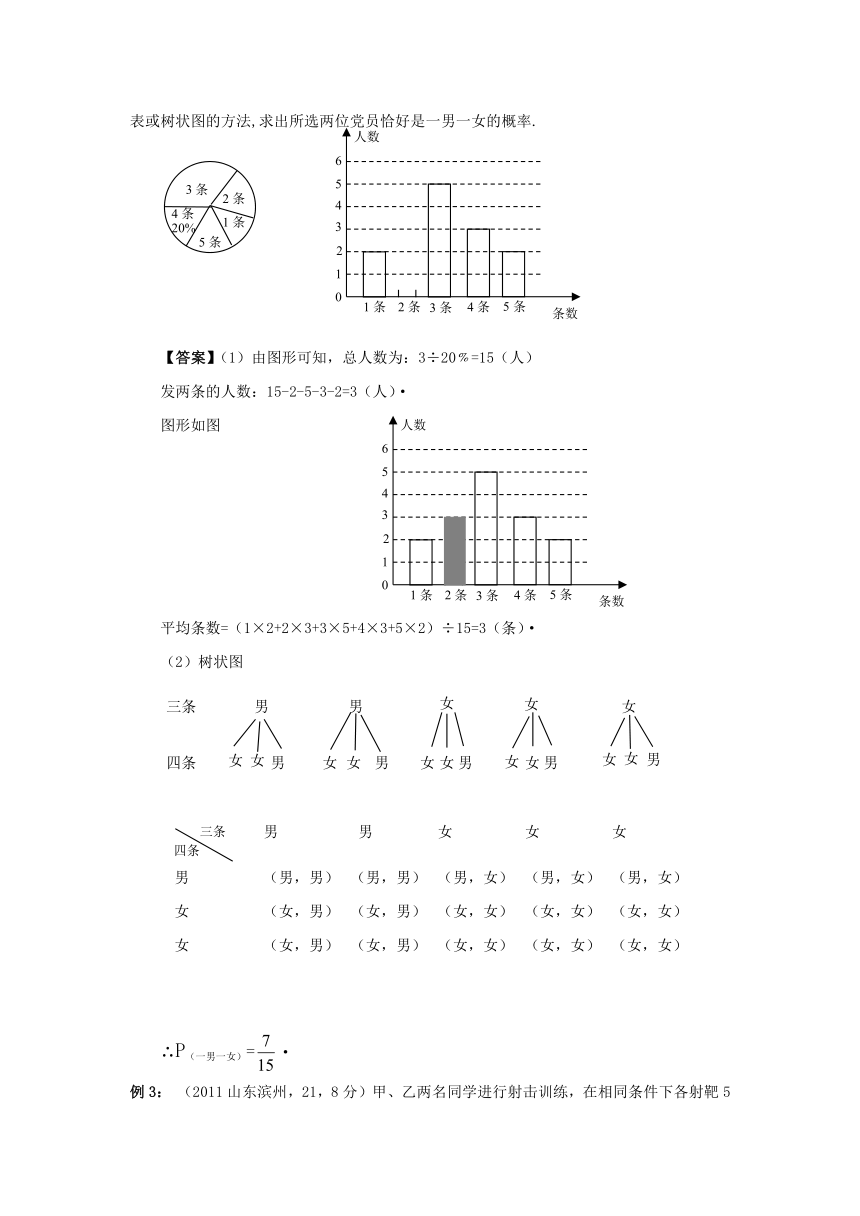
例2:( 2011重庆江津, 24,10分)在“传箴言”活动中,某党支部对全体党员在一个月内所发箴言条数情况进行了统计,并制成了如下两幅不完整的统计图.
(1)求该支部党员在这一个月内所发箴言的平均条数是多少 并将该条形统计图补充完整;
(2)如果发了三条箴言的党员中有两位男党员,发了四条箴言的党员有两位女党员,在发了三条箴言和四条箴言的党员中分别选出一位参加区委组织的“传箴言”活动总结会,请你用列表或树状图的方法,求出所选两位党员恰好是一男一女的概率.
【答案】(1)由图形可知,总人数为:3÷20﹪=15(人)
发两条的人数:15-2-5-3-2=3(人)·
图形如图
平均条数=(1×2+2×3+3×5+4×3+5×2)÷15=3(条)·
(2)树状图
男 男 女 女 女
男 (男,男) (男,男) (男,女) (男,女) (男,女)
女 (女,男) (女,男) (女,女) (女,女) (女,女)
女 (女,男) (女,男) (女,女) (女,女) (女,女)
∴P(一男一女)=·
例3: (2011山东滨州,21,8分)甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
命中环数 7 8 9 10
甲命中相应环数的次数 2 2 0 1
乙命中相应环数的次数 1 3 1 0
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则谁的射击成绩更稳定些?
答案:甲的平均数等于8,乙的平均数等于8
=1.2 =0.4
四、直击中考:
(一)选择题:
1.(2011四川重庆,5,4分)下列调查中,适宜采用抽样调查方式的是( )
A.调查我市中学生每天体育锻炼的时间
B.调查某班学生对“五个重庆”的知晓率
C.调查一架“歼20”隐形战机各零部件的质量
D.调查广州亚运会100米决赛参赛运动员兴奋剂的使用情况
2. (2011山东威海,2,3分)今年体育学业考试增加了跳绳测试项目,下面是测试时记录员记录的一组(10名)同学的测试成绩(单位:个/分钟).
176 180 184 180 170 176 172 164 186 180
该组数据的众数、中位数、平均数分别为( )
A.180, 180, 178 B.180, 178, 178
C.180, 178, 176.8 D.178, 180, 176.8
3、(2011江苏泰州,6,3分)为了了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是
A.某市八年级学生的肺活量 B.从中抽去的500名学生的肺活量
C.从中抽取的500名学生 D.500
4、2011山东聊城,8,3分)某小区20户家庭的日用电量(单位:千瓦时)统计如下:
日用电量(单位:千瓦时) 4 5 6 7 8 10
户数 1 3 6 5 4 1
这20户家庭日用电量的众数、中位数分别是( )
A. 6,6.5 B. 6,7 C. 6,7.5 D. 7,7.5
5.(2011山东临沂,10,3分)如图,A、B是数轴上的亮点,在线段AB上任取一点C,则点C到表示-1的点的距离不大于2的概率是( )
A. B. C. D.
6. 有下列事件:①367人中必有2人的生日相同;②抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于等于2;③在标准大气压下,温度低于0℃时冰融化;④如果a, b为实数,那么a+b=b+a.其中是必然事件的有( )
A.1个 B.2个 C.3个 D.4个
7. 在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是( )
A. B. C. D.
8. (2011山东枣庄,11,3分)在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是.如果再往盒中放进6颗黑色棋子,取得白色棋子的概率是,则原来盒中有白色棋子( )
A.8颗 B.6颗 C.4颗 D.2颗
(二)填空题:
9. (2011浙江义乌,12,4分)如果x1与x2的平均数是4,那么x1+1与x2+5的平均数是 .
5和5的方差是原来x1 x2 方差的____________倍
10如图是我市某景点6月份内1~10日每天的最高温度折线统计图,由图信息可知该景点这10天的最高气温度的中位数是 .
11.一鱼塘放养着鲤鱼、草鱼、鲢鱼共8000尾.小明想了解鱼
塘里各种鱼的情况,通过多次捕捞试验后发现鲤鱼、草鱼出现的概率分别为:31﹪和42﹪,则这个鱼塘里有鲢鱼___________.
12. 某班学生理化生实验操作测试成绩的统计结果如下表:
成绩/分 3 4 5 6 7 8 9 10
人数 1 1 2 2 8 9 15 12
则这些学生成绩的众数为 .
13. 从下面的6张牌中,任意抽取两张.其点数和是奇数的概率_________.
14. (2011四川凉山州,16,4分)如图,有三个同心圆,由里向外的半径依次是2cm,4cm, 6cm将圆盘分为三部分,飞镖可以落在任何一部分内,那么飞镖落在阴影圆环内的概率是 。
(三).解答题:
15. (2011浙江金华,20,8分)(本题8分)王大伯几年前承办了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如拆线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
16.(2011山东德州18,8分)2011年5月9日至14日,德州市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
等级 成绩(分) 频数(人数) 频率
A 90~100 19 0.38
B 75~89 m x
C 60~74 n y
D 60以下 3 0.06
合计 50 1.00
请你根据以上图表提供的信息,解答下列问题:
(1) m= ,n= ,x= ,y= ;
(2)在扇形图中,C等级所对应的圆心角是 度;
(3)如果该校九年级共有500名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?
17. (2011浙江义乌,20,8分)为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分
段(A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分)统计如下:
分数段 人数(人) 频率
A 48 0.2
B a 0.25
C 84 0.35
D 36 b
E 12 0.05
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为 ,b的值为 ,并将统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数. ”请问:甲同学的体育成绩应在什么分数段内? (填相应分数段的字母)
(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?
18. 如图所示的两个转盘,每个转盘分成几个相等的的扇形,甲、乙两个人做游戏,游戏者分别转动甲、乙两个转盘各一次;如果转盘A转出了红色,转盘B转出了蓝色,即两个转盘配成了紫色,则甲得3分,否则乙得1分。这个游戏对双方公平吗?说说你的理由。如果你认为不公平,应怎样修改得分规则才能使游戏对双方公平?
19、(2011浙江温州,21,10分)一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为,求n的值.
考点在线答案:
1、C 2、D 3、B 4、C 5、5.8 5800 6、
答案:
A 2、C 3、B 4、A 5、D 6、C 7、C 8、C
9、7 、25 10、24.5 11、2920 12、9 13、
14、
解答题
15、【解】(1)甲山上4棵树的产量分别为:50千克、36千克、40千克、34千克,所以甲山产量的样本平均数为:千克;
乙山上4棵树的产量分别为:36千克、40千克、48千克、36千克,所以乙山产量的样本平均数为:千克;
甲乙两山杨梅的产量总和为:2×100×98%×40=7840千克.
16、解:(1)20, 8, 0.4, 0.16
(2)57.6
(3)由上表可知达到优秀和良好的共有19+20=39人,
人.
17、解:(1) 60 , 0.15 (图略)
(2) C
(3)0.8×10440=8352(名)
答:该市九年级考生中体育成绩为优秀的学生人数约有8352名.
18 略
19、解:(1)
(3)由题意得,∴
经检验,n=4是所列方程的根,且符合题意.
人数
120
100
50
50
120
A级
B级
学习态度层级
C级
30
人数
120
100
50
50
120
A级
B级
C级
学习态度层级
图①
图②
25%
A级
B级
C级
60%
图②
3条
2条
1条
5条
4条
20%
1条
2条
3条
4条
5条
条数
人数
1
0
2
3
4
5
6
1条
2条
3条
4条
5条
条数
人数
1
0
2
3
4
5
6
四条
三条
男
男
男
男
男
男
男
女
女
女
女
女
女
女
女
女
女
女
女
女
三条
四条
D
C
A
A
B 40%
学业考试体育成绩(分数段)统计表
学业考试体育成绩(分数段)统计图
0
一、考点梳理:
平均数、众数、中位数的概念、统计图的应用、统计知识的综合利用(包括方差、频数、频率等概念)、.事件分类(包括、确定事件、必然事件、不可能事件)、概率的计算、公平性问题等。
二、考点在线:
1.(2011山东泰安,9 ,3分)某校篮球班21名同学的身高如下表:
身高(cm) 180 186 188 192 208
人数(个) 4 6 5 4 2
则该校篮球班21名同学身高的众数和中位数分别是(单位:cm)( )
A.186,186 B.186,187 C.186,188 D.208,188
2(2011广东湛江9,3分)甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均数都是环,方差分别是,, ,则射箭成绩最稳定的是
A甲 B乙 C丙 D丁
3.(2011福建福州,8,4分)从1,2,-3三个数中,随机抽取两个数相乘,积是正数的概率是( )
A.0 B. C. D. 1
4.(2011广东株洲,4,3分)株洲市关心下一代工作委员会为了了解全市初三学生的视力状况,从全市30000名初三学生中随机抽取了500人进行视力测试,发现其中视力不良的学生有100人,则可估计全市30000名初三学生中视力不良的约有( )
A.100人 B.500人 C.6000人 D.15000 人
5.(2011四川成都,22,4分)某校在“爱护地球 绿化祖图”的创建活动中,组织学生开展植树造林活动.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
植树数量(单位:棵) 4 5 6 8 10
人数 30 22 25 15 8
则这100名同学平均每人植树 __________棵;若该校共有1000名学生,请根据以上调查结果估计该校学生的植树总数是__________棵.
6. (2011四川内江,13,5分)“Welcome to Senior High School.”(欢迎进入高中),在这段句子的所有英文字母中,字母o出现的频率是 .
三、精典剖析:
例1:(2011山东菏泽,19,10分)初中生对待学习的态度一直是教育工作者关注的问题之一.为此菏泽市教育局对我市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
(1)200;
(2)200-120-50=30(人).画图正确.
(3)C所占圆心角度数=360°×(1-25%-60%)=54°.
(4)12000×(25%+60%)=10200.
∴估计该市初中生中大约有10200名学生学习态度达标.
例2:( 2011重庆江津, 24,10分)在“传箴言”活动中,某党支部对全体党员在一个月内所发箴言条数情况进行了统计,并制成了如下两幅不完整的统计图.
(1)求该支部党员在这一个月内所发箴言的平均条数是多少 并将该条形统计图补充完整;
(2)如果发了三条箴言的党员中有两位男党员,发了四条箴言的党员有两位女党员,在发了三条箴言和四条箴言的党员中分别选出一位参加区委组织的“传箴言”活动总结会,请你用列表或树状图的方法,求出所选两位党员恰好是一男一女的概率.
【答案】(1)由图形可知,总人数为:3÷20﹪=15(人)
发两条的人数:15-2-5-3-2=3(人)·
图形如图
平均条数=(1×2+2×3+3×5+4×3+5×2)÷15=3(条)·
(2)树状图
男 男 女 女 女
男 (男,男) (男,男) (男,女) (男,女) (男,女)
女 (女,男) (女,男) (女,女) (女,女) (女,女)
女 (女,男) (女,男) (女,女) (女,女) (女,女)
∴P(一男一女)=·
例3: (2011山东滨州,21,8分)甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
命中环数 7 8 9 10
甲命中相应环数的次数 2 2 0 1
乙命中相应环数的次数 1 3 1 0
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则谁的射击成绩更稳定些?
答案:甲的平均数等于8,乙的平均数等于8
=1.2 =0.4
四、直击中考:
(一)选择题:
1.(2011四川重庆,5,4分)下列调查中,适宜采用抽样调查方式的是( )
A.调查我市中学生每天体育锻炼的时间
B.调查某班学生对“五个重庆”的知晓率
C.调查一架“歼20”隐形战机各零部件的质量
D.调查广州亚运会100米决赛参赛运动员兴奋剂的使用情况
2. (2011山东威海,2,3分)今年体育学业考试增加了跳绳测试项目,下面是测试时记录员记录的一组(10名)同学的测试成绩(单位:个/分钟).
176 180 184 180 170 176 172 164 186 180
该组数据的众数、中位数、平均数分别为( )
A.180, 180, 178 B.180, 178, 178
C.180, 178, 176.8 D.178, 180, 176.8
3、(2011江苏泰州,6,3分)为了了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是
A.某市八年级学生的肺活量 B.从中抽去的500名学生的肺活量
C.从中抽取的500名学生 D.500
4、2011山东聊城,8,3分)某小区20户家庭的日用电量(单位:千瓦时)统计如下:
日用电量(单位:千瓦时) 4 5 6 7 8 10
户数 1 3 6 5 4 1
这20户家庭日用电量的众数、中位数分别是( )
A. 6,6.5 B. 6,7 C. 6,7.5 D. 7,7.5
5.(2011山东临沂,10,3分)如图,A、B是数轴上的亮点,在线段AB上任取一点C,则点C到表示-1的点的距离不大于2的概率是( )
A. B. C. D.
6. 有下列事件:①367人中必有2人的生日相同;②抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于等于2;③在标准大气压下,温度低于0℃时冰融化;④如果a, b为实数,那么a+b=b+a.其中是必然事件的有( )
A.1个 B.2个 C.3个 D.4个
7. 在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是( )
A. B. C. D.
8. (2011山东枣庄,11,3分)在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是.如果再往盒中放进6颗黑色棋子,取得白色棋子的概率是,则原来盒中有白色棋子( )
A.8颗 B.6颗 C.4颗 D.2颗
(二)填空题:
9. (2011浙江义乌,12,4分)如果x1与x2的平均数是4,那么x1+1与x2+5的平均数是 .
5和5的方差是原来x1 x2 方差的____________倍
10如图是我市某景点6月份内1~10日每天的最高温度折线统计图,由图信息可知该景点这10天的最高气温度的中位数是 .
11.一鱼塘放养着鲤鱼、草鱼、鲢鱼共8000尾.小明想了解鱼
塘里各种鱼的情况,通过多次捕捞试验后发现鲤鱼、草鱼出现的概率分别为:31﹪和42﹪,则这个鱼塘里有鲢鱼___________.
12. 某班学生理化生实验操作测试成绩的统计结果如下表:
成绩/分 3 4 5 6 7 8 9 10
人数 1 1 2 2 8 9 15 12
则这些学生成绩的众数为 .
13. 从下面的6张牌中,任意抽取两张.其点数和是奇数的概率_________.
14. (2011四川凉山州,16,4分)如图,有三个同心圆,由里向外的半径依次是2cm,4cm, 6cm将圆盘分为三部分,飞镖可以落在任何一部分内,那么飞镖落在阴影圆环内的概率是 。
(三).解答题:
15. (2011浙江金华,20,8分)(本题8分)王大伯几年前承办了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如拆线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
16.(2011山东德州18,8分)2011年5月9日至14日,德州市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
等级 成绩(分) 频数(人数) 频率
A 90~100 19 0.38
B 75~89 m x
C 60~74 n y
D 60以下 3 0.06
合计 50 1.00
请你根据以上图表提供的信息,解答下列问题:
(1) m= ,n= ,x= ,y= ;
(2)在扇形图中,C等级所对应的圆心角是 度;
(3)如果该校九年级共有500名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?
17. (2011浙江义乌,20,8分)为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分
段(A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分)统计如下:
分数段 人数(人) 频率
A 48 0.2
B a 0.25
C 84 0.35
D 36 b
E 12 0.05
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为 ,b的值为 ,并将统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数. ”请问:甲同学的体育成绩应在什么分数段内? (填相应分数段的字母)
(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?
18. 如图所示的两个转盘,每个转盘分成几个相等的的扇形,甲、乙两个人做游戏,游戏者分别转动甲、乙两个转盘各一次;如果转盘A转出了红色,转盘B转出了蓝色,即两个转盘配成了紫色,则甲得3分,否则乙得1分。这个游戏对双方公平吗?说说你的理由。如果你认为不公平,应怎样修改得分规则才能使游戏对双方公平?
19、(2011浙江温州,21,10分)一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅匀,再摸出1个球,求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅匀后,使摸出1个球是白球的概率为,求n的值.
考点在线答案:
1、C 2、D 3、B 4、C 5、5.8 5800 6、
答案:
A 2、C 3、B 4、A 5、D 6、C 7、C 8、C
9、7 、25 10、24.5 11、2920 12、9 13、
14、
解答题
15、【解】(1)甲山上4棵树的产量分别为:50千克、36千克、40千克、34千克,所以甲山产量的样本平均数为:千克;
乙山上4棵树的产量分别为:36千克、40千克、48千克、36千克,所以乙山产量的样本平均数为:千克;
甲乙两山杨梅的产量总和为:2×100×98%×40=7840千克.
16、解:(1)20, 8, 0.4, 0.16
(2)57.6
(3)由上表可知达到优秀和良好的共有19+20=39人,
人.
17、解:(1) 60 , 0.15 (图略)
(2) C
(3)0.8×10440=8352(名)
答:该市九年级考生中体育成绩为优秀的学生人数约有8352名.
18 略
19、解:(1)
(3)由题意得,∴
经检验,n=4是所列方程的根,且符合题意.
人数
120
100
50
50
120
A级
B级
学习态度层级
C级
30
人数
120
100
50
50
120
A级
B级
C级
学习态度层级
图①
图②
25%
A级
B级
C级
60%
图②
3条
2条
1条
5条
4条
20%
1条
2条
3条
4条
5条
条数
人数
1
0
2
3
4
5
6
1条
2条
3条
4条
5条
条数
人数
1
0
2
3
4
5
6
四条
三条
男
男
男
男
男
男
男
女
女
女
女
女
女
女
女
女
女
女
女
女
三条
四条
D
C
A
A
B 40%
学业考试体育成绩(分数段)统计表
学业考试体育成绩(分数段)统计图
0
同课章节目录
