2012年中考第一轮复习精品教学案:十、相似形
文档属性
| 名称 | 2012年中考第一轮复习精品教学案:十、相似形 |

|
|
| 格式 | zip | ||
| 文件大小 | 262.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-15 00:00:00 | ||
图片预览

文档简介
十、相 似 形 (王瓜店中学 郭剑 王艳花)
一、学习目标
1、了解比例的基本性质、线段的比、成比例线段;2、通过具体实例认识图形的相似,理解相似图形的性质,相似多边形的对应角相等,对应边成比例,面积的比等于对应边比的平方;3、了解两个三角形相似的概念,理解两个三角形的相似的条件;4、了解图形的位似,灵活运用位似将一个图形放大或缩小;5、灵活运用图形的相似解决一些实际问题.
二、知识要点
1、比例的基本性质、线段的比、成比例线段;
2、三角形相似的概念和性质,三角形相似的条件;
3、相似多边形的性质;
4、图形的放大与缩小.
三、考点再现
1、((2011浙江台州)若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
A. 1:2 B. 1:4 C. 1:5 D. 1:16
2、(2011广东肇庆)如图,已知直线a∥b∥c,直线m、n 与a、b、c分别交于点A、C、E、B、D、F,AC = 4,CE = 6,BD = 3,则BF =
A. 7 B. 7.5 C. 8 D. 8.5
3、(2011广东中山)将左下图中的箭头缩小到原来的,得到的图形是( )
4、(2011湖南怀化)如图3所示:△ABC中,DE∥BC,AD=5,BD=10,AE=3,则CE的值为( )
A.9 B.6 C.3 D.4
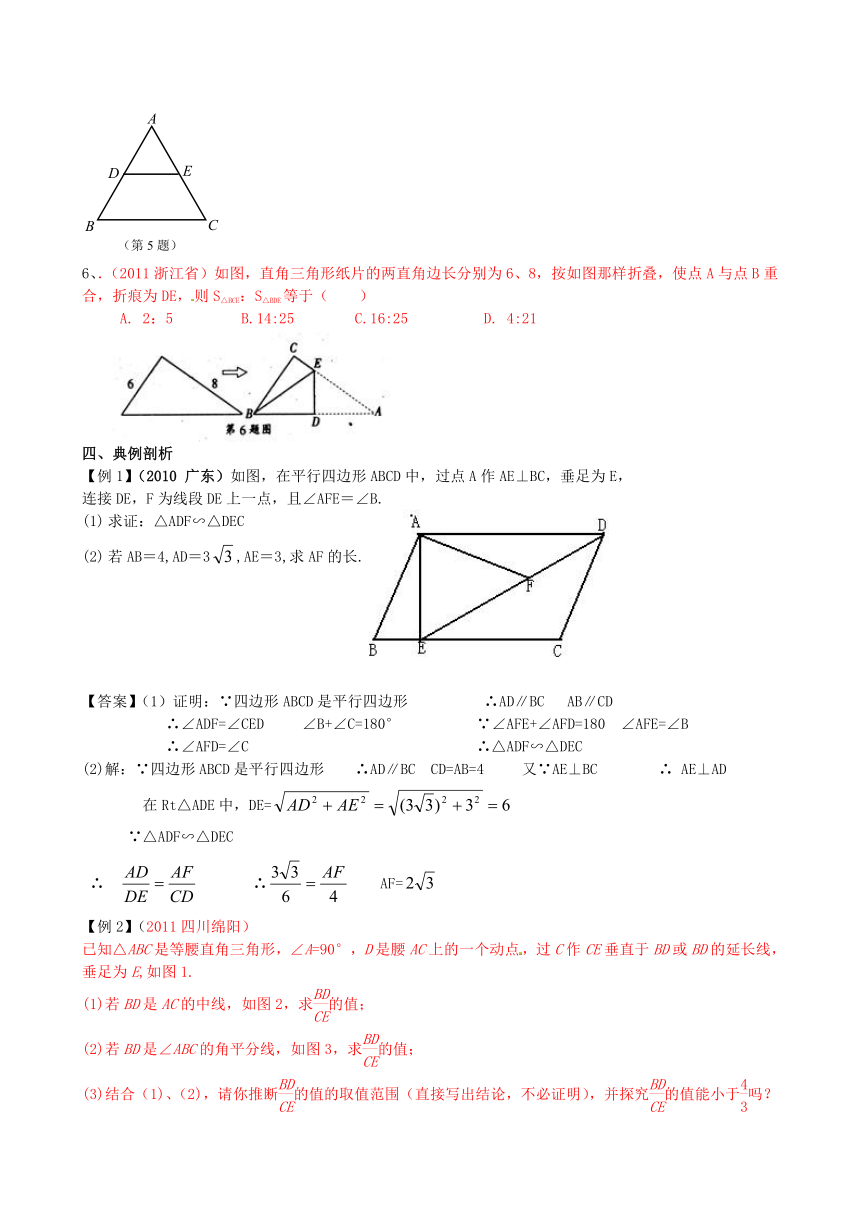
5、(2011浙江省嘉兴)如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为( )
(A) (B) (C) (D)
6、.(2011浙江省)如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )
A. 2:5 B.14:25 C.16:25 D. 4:21
四、典例剖析
【例1】(2010 广东)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,
连接DE,F为线段DE上一点,且∠AFE=∠B.
求证:△ADF∽△DEC
若AB=4,AD=3,AE=3,求AF的长.
【答案】(1)证明:∵四边形ABCD是平行四边形 ∴AD∥BC AB∥CD
∴∠ADF=∠CED ∠B+∠C=180° ∵∠AFE+∠AFD=180 ∠AFE=∠B
∴∠AFD=∠C ∴△ADF∽△DEC
(2)解:∵四边形ABCD是平行四边形 ∴AD∥BC CD=AB=4 又∵AE⊥BC ∴ AE⊥AD
在Rt△ADE中,DE=
∵△ADF∽△DEC
∴ ∴ AF=
【例2】(2011四川绵阳)
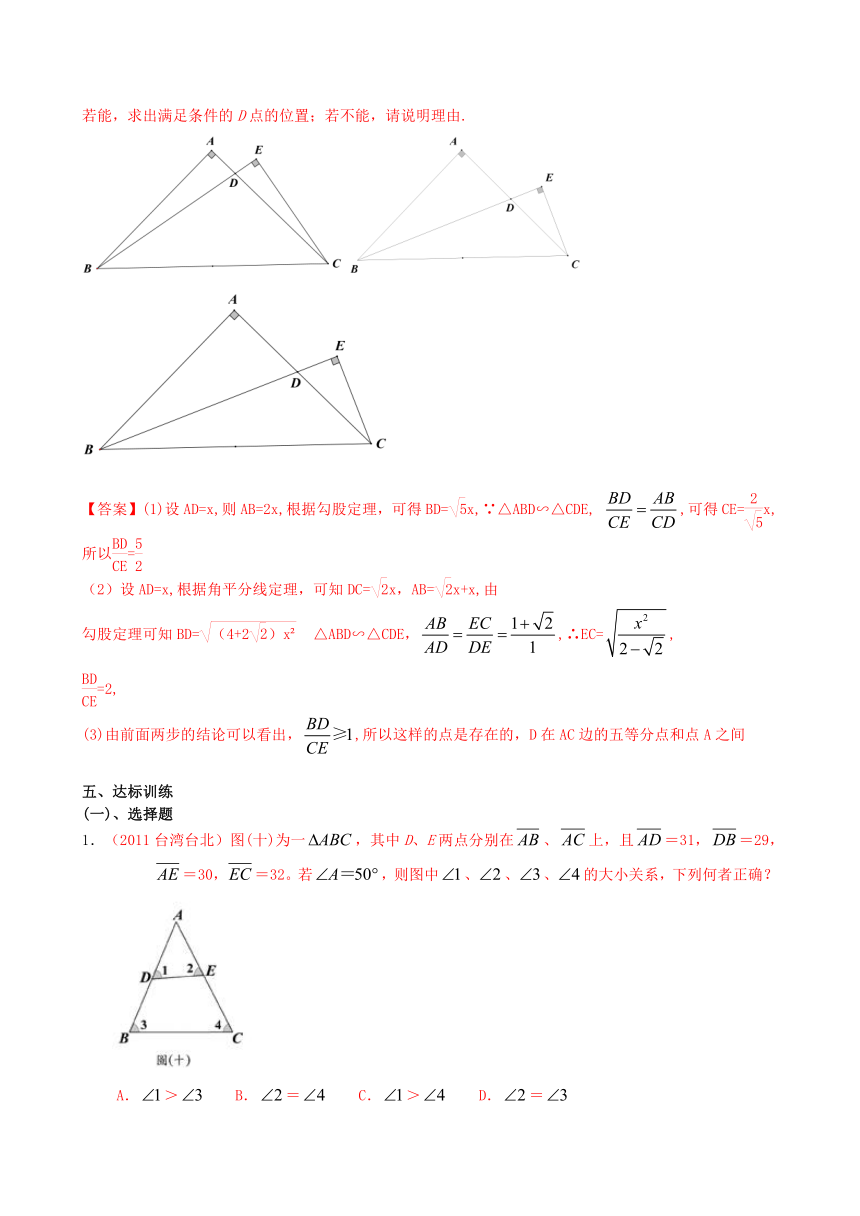
已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过C作CE垂直于BD或BD的延长线,垂足为E,如图1.
(1)若BD是AC的中线,如图2,求的值;
(2)若BD是∠ABC的角平分线,如图3,求的值;
(3)结合(1)、(2),请你推断的值的取值范围(直接写出结论,不必证明),并探究的值能小于吗?若能,求出满足条件的D点的位置;若不能,请说明理由.
【答案】(1)设AD=x,则AB=2x,根据勾股定理,可得BD=x,∵△ABD∽△CDE, ,可得CE= EQ \f(2,)x,所以=
(2)设AD=x,根据角平分线定理,可知DC=x,AB=x+x,由
勾股定理可知BD= EQ \r(,(4+2)x ) △ABD∽△CDE,,∴EC=,
=2,
(3)由前面两步的结论可以看出,,所以这样的点是存在的,D在AC边的五等分点和点A之间
五、达标训练
(一)、选择题
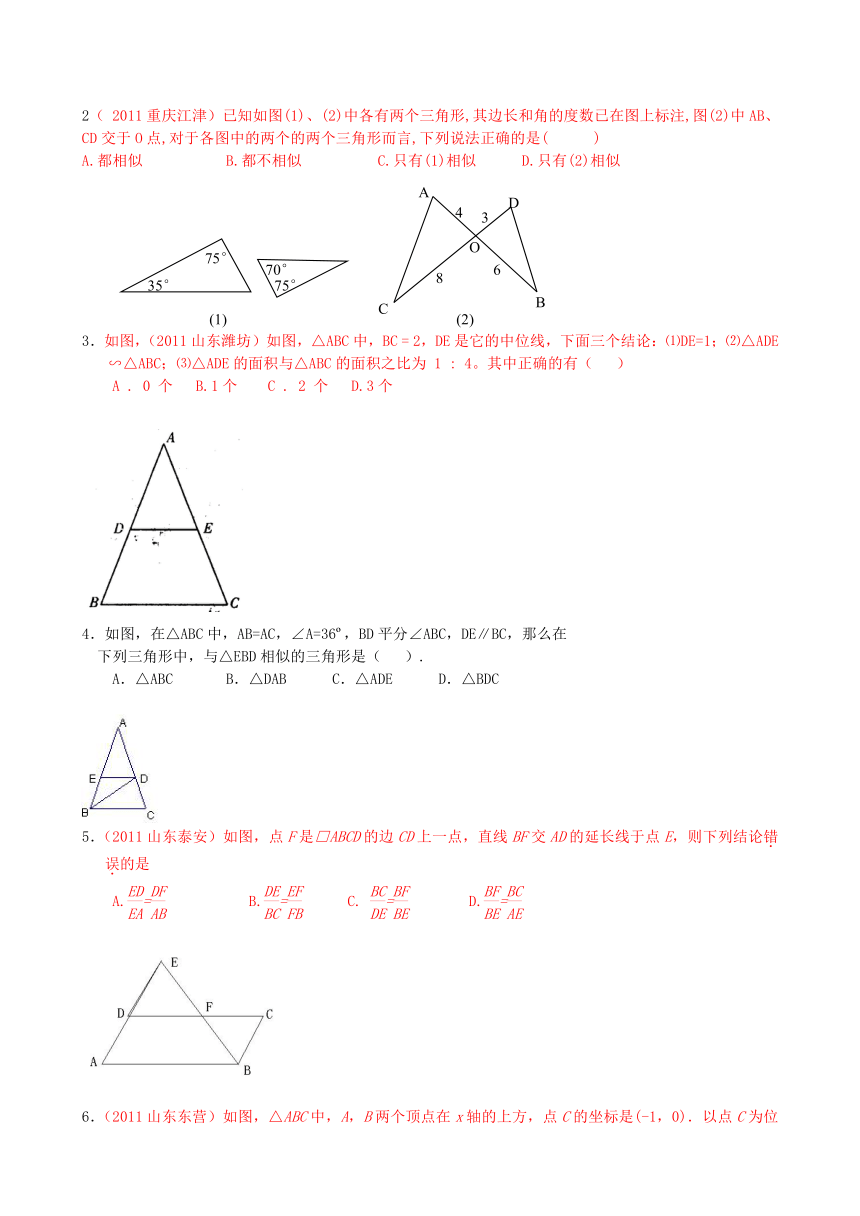
1.(2011台湾台北)图(十)为一,其中D、E两点分别在、上,且=31,=29,=30,=32。若,则图中、、、的大小关系,下列何者正确?
A.> B.= C.> D.=
2( 2011重庆江津)已知如图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于O点,对于各图中的两个的两个三角形而言,下列说法正确的是( )
A.都相似 B.都不相似 C.只有(1)相似 D.只有(2)相似
3.如图,(2011山东潍坊)如图,△ABC中,BC = 2,DE是它的中位线,下面三个结论:⑴DE=1;⑵△ADE∽△ABC;⑶△ADE的面积与△ABC的面积之比为 1 : 4。其中正确的有( )
A . 0 个 B.1个 C . 2 个 D.3个
4.如图,在△ABC中,AB=AC,∠A=36 ,BD平分∠ABC,DE∥BC,那么在
下列三角形中,与△EBD相似的三角形是( ).
A.△ABC B.△DAB C.△ADE D.△BDC
5.(2011山东泰安)如图,点F是□ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是
A.= B.= C. = D.=
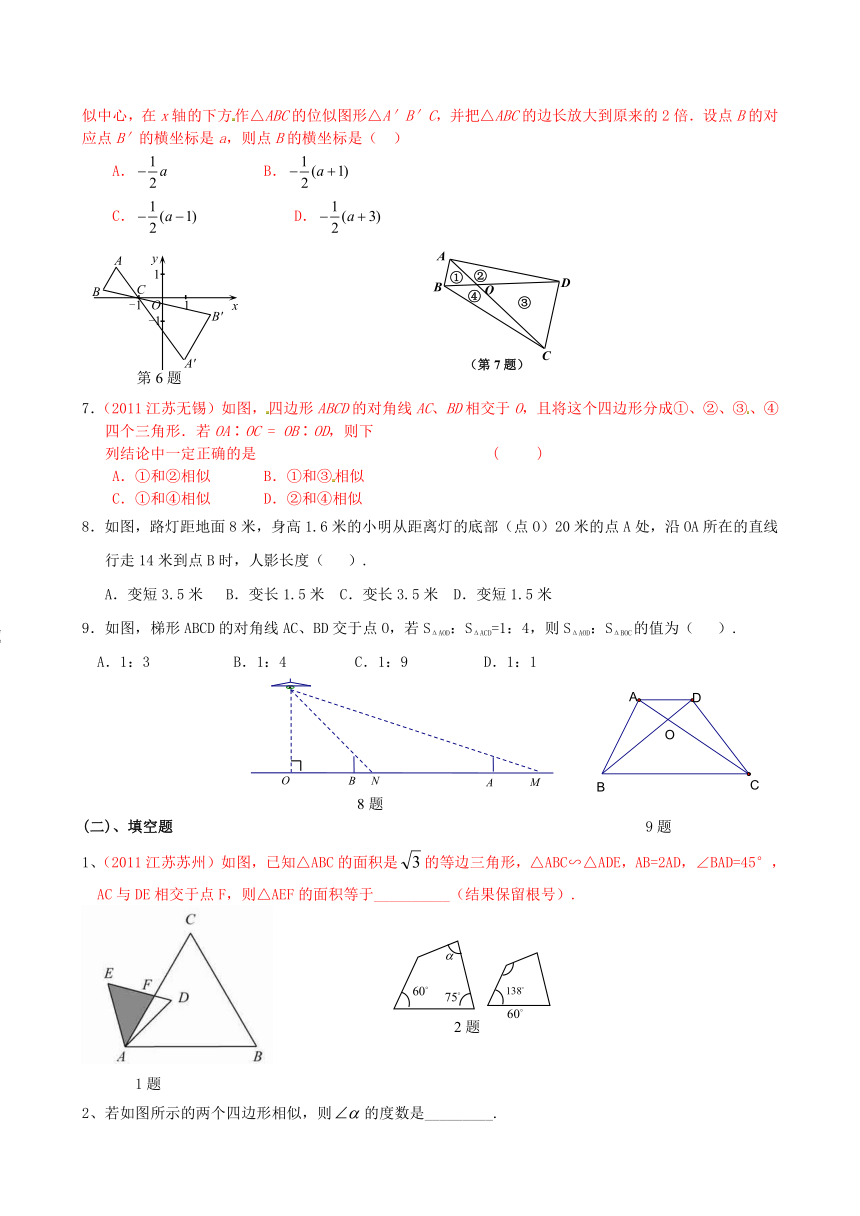
6.(2011山东东营)如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. B.
C. D.
7.(2011江苏无锡)如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA∶OC = OB∶OD,则下
列结论中一定正确的是 ( )
A.①和②相似 B.①和③相似
C.①和④相似 D.②和④相似
8.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影长度( ).
A.变短3.5米 B.变长1.5米 C.变长3.5米 D.变短1.5米
9.如图,梯形ABCD的对角线AC、BD交于点O,若SΔAOD:SΔACD=1:4,则SΔAOD:SΔBOC的值为( ).
A.1:3 B.1:4 C.1:9 D.1:1
(二)、填空题 9题
1、(2011江苏苏州)如图,已知△ABC的面积是的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于__________(结果保留根号).
1题
2、若如图所示的两个四边形相似,则的度数是_________.
3、(2011深圳).如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边为39,那么较大的三角形的周长 ,面积 .
4.如图,一油桶高0.8 m,桶内有油,一根木棒长1m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长0.8m,则桶内油的高度为_________.
5、(2010兰州) 如上图,上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是 米.
6.(2010 重庆)已知△与△相似且对应中线的比为,则△与△的周长比为 .
(三)、解答下列各题
1.(2011杭州)如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外)。连结EB,过E作EF⊥ AB,交AB的延长线为F。
(1)猜测直线BE和直线AC的位置关系,并证明你的猜想。
(2)证明:△BEF∽△ABC,并求出相似比。
2.(2010 台州)如图,在△ABC中,D是BC边上一点,E是AC边上一点.且满足AD=AB,∠ADE=∠C.
(1)求证:∠AED=∠ADC,∠DEC=∠B;
(2)求证:AB2=AE AC.
3.(2011河北)如图10,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的顶点.
(1)以O为位似中心,在网格图中作△A′B′C′和△ABC位似,且位似比为1︰2;
(2)连接(1)中的AA′,求四边形AA′C′C的周长.(结果保留根号)
4.如图,正方形MNPQ的顶点在三角形ABC的边上,当边BC=a与高AD=h
满足什么条件时,正方形MNPQ的面积是三角形ABC面积的一半?
5.某社区拟筹资金2000元,计划在一块上、下底分别是10米、20米的梯形空地上
种植花木(如图所示),他们想在地带种植单价为10元/米2的太阳花,
当地带种满花后,已经花了500元,请你预算一下,若继续在地带种植
同样的太阳花,资金是否够用?并说明理由.
6.(2010江苏淮安)如(a)图,在平面直角坐标系中,点A坐标为(12,0),点B坐标为(6,8),点C为OB的中点,点D从点O出发,沿△OAB的三边按逆时针方向以2个单位长度/秒的速度运动一周.
(1)点C坐标是( , ),当点D运动8.5秒时所在位置的坐标是( , );
(2)设点D运动的时间为t秒,试用含t的代数式表示△OCD的面积S,并指出t为何值
时,S最大;
(3)点E在线段AB上以同样速度由点A向点B运动,如(b)图,若点E与点D同时
出发,问在运动5秒钟内,以点D,A,E为顶点的三角形何时与△OCD相似(只考虑以
点A.O为对应顶点的情况):
题6(a)图 题6(b)图
六、学习感悟
十、相似形 参考答案
考点再现:A B A B B B
达标训练
一 D A D B; C; D; B; A; A;
二 1 2. 87°; 3.90,270; 0.64m; 6米; 2:3
三 (1)【答案】解:(1)猜测BE和直线AC垂直 …………1分
证明△AEB≌△CEB(SSS) …………2分
说明EB是∠AEC的平分线,再利用等腰△三线合一即可 …………2分
(2)证明∠EBF=45°即可证明△BEF∽△ABC \…………2分
延长EB交AC于G,设AC为2a,则BG=a,EB=,
所以
(2)【答案】
证明:(1)在△ADE和△ACD中
∵∠ADE=∠C,∠DAE=∠DAE
∴∠AED=180°-∠DAE-∠ADE
∠ADC=180°-∠DAE-∠C
∴∠AED=∠ADC
∵∠AED+∠DEC=180°
∠ADB+∠ADC=180°
∴∠DEC=∠ADB
又∵AB=AD
∴∠ADB=∠B
∴∠DEC=∠B
(2)在△ADE和△ACD中
由(1)知∠ADE=∠C,∠DAE=∠DAE
∴△ADE∽△ACD
∴
即AD2=AE AC
又∵AB=AD
∴AB2=AE AC
(3)【答案】(1)如下图.
(2)四边形AA′C′C的周长=4+6
(4) 略(5) 略
(6)【答案】解:(1)C(3,4)、D(9,4)
(2)当D在OA上运动时,(0<t<6);
当D在AB上运动时,过点O作OE⊥AB,过点C作CF⊥AB,垂足分别为E和F,过D作DM⊥OA,过B作BN⊥OA,垂足分别为M和N,如图:
设D点运动的时间为t秒,所以DA=2t-12,BD=22-2t,
又因为C为OB的中点,
所以BF为△BOE的中位线,
所以,
又因为,
所以,
所以,
因为BN⊥OA,DM⊥OA,
所以△ADM∽△ABN,
所以,
所以,
又因为,
所以,
即(6≤t<11),
所以当t=6时,△OCD面积最大,为;
当D在OB上运动时,O、C、D在同一直线上,S=0(11≤t≤16).
(3)设当运动t秒时,△OCD∽△ADE,则,即,所以t=3.5;
设当运动t秒时,△OCD∽△AED,则,即,所以,所以,(舍去),
所以当t为3.5秒或秒时两三角形相似.
a
b
c
A
B
C
D
E
F
m
n
(第5题)
35°
75°
75°
70°
(1)
A
B
C
D
O
4
3
6
8
(2)
A
B
C
D
O
①
②⊙o⊙
③⊙o⊙
④⊙o⊙
(第7题)
B′
A′
第6题
-1
x
1
O
-1
1
y
B
A
C
4题
O
D
C
B
A
O
B
N
A
M
8题
EMBED Equation.DSMT4
2题
10米
20米
B
M
D
A
一、学习目标
1、了解比例的基本性质、线段的比、成比例线段;2、通过具体实例认识图形的相似,理解相似图形的性质,相似多边形的对应角相等,对应边成比例,面积的比等于对应边比的平方;3、了解两个三角形相似的概念,理解两个三角形的相似的条件;4、了解图形的位似,灵活运用位似将一个图形放大或缩小;5、灵活运用图形的相似解决一些实际问题.
二、知识要点
1、比例的基本性质、线段的比、成比例线段;
2、三角形相似的概念和性质,三角形相似的条件;
3、相似多边形的性质;
4、图形的放大与缩小.
三、考点再现
1、((2011浙江台州)若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
A. 1:2 B. 1:4 C. 1:5 D. 1:16
2、(2011广东肇庆)如图,已知直线a∥b∥c,直线m、n 与a、b、c分别交于点A、C、E、B、D、F,AC = 4,CE = 6,BD = 3,则BF =
A. 7 B. 7.5 C. 8 D. 8.5
3、(2011广东中山)将左下图中的箭头缩小到原来的,得到的图形是( )
4、(2011湖南怀化)如图3所示:△ABC中,DE∥BC,AD=5,BD=10,AE=3,则CE的值为( )
A.9 B.6 C.3 D.4
5、(2011浙江省嘉兴)如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为( )
(A) (B) (C) (D)
6、.(2011浙江省)如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )
A. 2:5 B.14:25 C.16:25 D. 4:21
四、典例剖析
【例1】(2010 广东)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,
连接DE,F为线段DE上一点,且∠AFE=∠B.
求证:△ADF∽△DEC
若AB=4,AD=3,AE=3,求AF的长.
【答案】(1)证明:∵四边形ABCD是平行四边形 ∴AD∥BC AB∥CD
∴∠ADF=∠CED ∠B+∠C=180° ∵∠AFE+∠AFD=180 ∠AFE=∠B
∴∠AFD=∠C ∴△ADF∽△DEC
(2)解:∵四边形ABCD是平行四边形 ∴AD∥BC CD=AB=4 又∵AE⊥BC ∴ AE⊥AD
在Rt△ADE中,DE=
∵△ADF∽△DEC
∴ ∴ AF=
【例2】(2011四川绵阳)
已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过C作CE垂直于BD或BD的延长线,垂足为E,如图1.
(1)若BD是AC的中线,如图2,求的值;
(2)若BD是∠ABC的角平分线,如图3,求的值;
(3)结合(1)、(2),请你推断的值的取值范围(直接写出结论,不必证明),并探究的值能小于吗?若能,求出满足条件的D点的位置;若不能,请说明理由.
【答案】(1)设AD=x,则AB=2x,根据勾股定理,可得BD=x,∵△ABD∽△CDE, ,可得CE= EQ \f(2,)x,所以=
(2)设AD=x,根据角平分线定理,可知DC=x,AB=x+x,由
勾股定理可知BD= EQ \r(,(4+2)x ) △ABD∽△CDE,,∴EC=,
=2,
(3)由前面两步的结论可以看出,,所以这样的点是存在的,D在AC边的五等分点和点A之间
五、达标训练
(一)、选择题
1.(2011台湾台北)图(十)为一,其中D、E两点分别在、上,且=31,=29,=30,=32。若,则图中、、、的大小关系,下列何者正确?
A.> B.= C.> D.=
2( 2011重庆江津)已知如图(1)、(2)中各有两个三角形,其边长和角的度数已在图上标注,图(2)中AB、CD交于O点,对于各图中的两个的两个三角形而言,下列说法正确的是( )
A.都相似 B.都不相似 C.只有(1)相似 D.只有(2)相似
3.如图,(2011山东潍坊)如图,△ABC中,BC = 2,DE是它的中位线,下面三个结论:⑴DE=1;⑵△ADE∽△ABC;⑶△ADE的面积与△ABC的面积之比为 1 : 4。其中正确的有( )
A . 0 个 B.1个 C . 2 个 D.3个
4.如图,在△ABC中,AB=AC,∠A=36 ,BD平分∠ABC,DE∥BC,那么在
下列三角形中,与△EBD相似的三角形是( ).
A.△ABC B.△DAB C.△ADE D.△BDC
5.(2011山东泰安)如图,点F是□ABCD的边CD上一点,直线BF交AD的延长线于点E,则下列结论错误的是
A.= B.= C. = D.=
6.(2011山东东营)如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. B.
C. D.
7.(2011江苏无锡)如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA∶OC = OB∶OD,则下
列结论中一定正确的是 ( )
A.①和②相似 B.①和③相似
C.①和④相似 D.②和④相似
8.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影长度( ).
A.变短3.5米 B.变长1.5米 C.变长3.5米 D.变短1.5米
9.如图,梯形ABCD的对角线AC、BD交于点O,若SΔAOD:SΔACD=1:4,则SΔAOD:SΔBOC的值为( ).
A.1:3 B.1:4 C.1:9 D.1:1
(二)、填空题 9题
1、(2011江苏苏州)如图,已知△ABC的面积是的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于__________(结果保留根号).
1题
2、若如图所示的两个四边形相似,则的度数是_________.
3、(2011深圳).如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边为39,那么较大的三角形的周长 ,面积 .
4.如图,一油桶高0.8 m,桶内有油,一根木棒长1m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长0.8m,则桶内油的高度为_________.
5、(2010兰州) 如上图,上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是 米.
6.(2010 重庆)已知△与△相似且对应中线的比为,则△与△的周长比为 .
(三)、解答下列各题
1.(2011杭州)如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外)。连结EB,过E作EF⊥ AB,交AB的延长线为F。
(1)猜测直线BE和直线AC的位置关系,并证明你的猜想。
(2)证明:△BEF∽△ABC,并求出相似比。
2.(2010 台州)如图,在△ABC中,D是BC边上一点,E是AC边上一点.且满足AD=AB,∠ADE=∠C.
(1)求证:∠AED=∠ADC,∠DEC=∠B;
(2)求证:AB2=AE AC.
3.(2011河北)如图10,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的顶点.
(1)以O为位似中心,在网格图中作△A′B′C′和△ABC位似,且位似比为1︰2;
(2)连接(1)中的AA′,求四边形AA′C′C的周长.(结果保留根号)
4.如图,正方形MNPQ的顶点在三角形ABC的边上,当边BC=a与高AD=h
满足什么条件时,正方形MNPQ的面积是三角形ABC面积的一半?
5.某社区拟筹资金2000元,计划在一块上、下底分别是10米、20米的梯形空地上
种植花木(如图所示),他们想在地带种植单价为10元/米2的太阳花,
当地带种满花后,已经花了500元,请你预算一下,若继续在地带种植
同样的太阳花,资金是否够用?并说明理由.
6.(2010江苏淮安)如(a)图,在平面直角坐标系中,点A坐标为(12,0),点B坐标为(6,8),点C为OB的中点,点D从点O出发,沿△OAB的三边按逆时针方向以2个单位长度/秒的速度运动一周.
(1)点C坐标是( , ),当点D运动8.5秒时所在位置的坐标是( , );
(2)设点D运动的时间为t秒,试用含t的代数式表示△OCD的面积S,并指出t为何值
时,S最大;
(3)点E在线段AB上以同样速度由点A向点B运动,如(b)图,若点E与点D同时
出发,问在运动5秒钟内,以点D,A,E为顶点的三角形何时与△OCD相似(只考虑以
点A.O为对应顶点的情况):
题6(a)图 题6(b)图
六、学习感悟
十、相似形 参考答案
考点再现:A B A B B B
达标训练
一 D A D B; C; D; B; A; A;
二 1 2. 87°; 3.90,270; 0.64m; 6米; 2:3
三 (1)【答案】解:(1)猜测BE和直线AC垂直 …………1分
证明△AEB≌△CEB(SSS) …………2分
说明EB是∠AEC的平分线,再利用等腰△三线合一即可 …………2分
(2)证明∠EBF=45°即可证明△BEF∽△ABC \…………2分
延长EB交AC于G,设AC为2a,则BG=a,EB=,
所以
(2)【答案】
证明:(1)在△ADE和△ACD中
∵∠ADE=∠C,∠DAE=∠DAE
∴∠AED=180°-∠DAE-∠ADE
∠ADC=180°-∠DAE-∠C
∴∠AED=∠ADC
∵∠AED+∠DEC=180°
∠ADB+∠ADC=180°
∴∠DEC=∠ADB
又∵AB=AD
∴∠ADB=∠B
∴∠DEC=∠B
(2)在△ADE和△ACD中
由(1)知∠ADE=∠C,∠DAE=∠DAE
∴△ADE∽△ACD
∴
即AD2=AE AC
又∵AB=AD
∴AB2=AE AC
(3)【答案】(1)如下图.
(2)四边形AA′C′C的周长=4+6
(4) 略(5) 略
(6)【答案】解:(1)C(3,4)、D(9,4)
(2)当D在OA上运动时,(0<t<6);
当D在AB上运动时,过点O作OE⊥AB,过点C作CF⊥AB,垂足分别为E和F,过D作DM⊥OA,过B作BN⊥OA,垂足分别为M和N,如图:
设D点运动的时间为t秒,所以DA=2t-12,BD=22-2t,
又因为C为OB的中点,
所以BF为△BOE的中位线,
所以,
又因为,
所以,
所以,
因为BN⊥OA,DM⊥OA,
所以△ADM∽△ABN,
所以,
所以,
又因为,
所以,
即(6≤t<11),
所以当t=6时,△OCD面积最大,为;
当D在OB上运动时,O、C、D在同一直线上,S=0(11≤t≤16).
(3)设当运动t秒时,△OCD∽△ADE,则,即,所以t=3.5;
设当运动t秒时,△OCD∽△AED,则,即,所以,所以,(舍去),
所以当t为3.5秒或秒时两三角形相似.
a
b
c
A
B
C
D
E
F
m
n
(第5题)
35°
75°
75°
70°
(1)
A
B
C
D
O
4
3
6
8
(2)
A
B
C
D
O
①
②⊙o⊙
③⊙o⊙
④⊙o⊙
(第7题)
B′
A′
第6题
-1
x
1
O
-1
1
y
B
A
C
4题
O
D
C
B
A
O
B
N
A
M
8题
EMBED Equation.DSMT4
2题
10米
20米
B
M
D
A
同课章节目录
