3.3函数的应用(—)-【新教材】人教B版(2019)高中数学必修第一册同步提高练习(Word含答案)
文档属性
| 名称 | 3.3函数的应用(—)-【新教材】人教B版(2019)高中数学必修第一册同步提高练习(Word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 00:16:36 | ||
图片预览


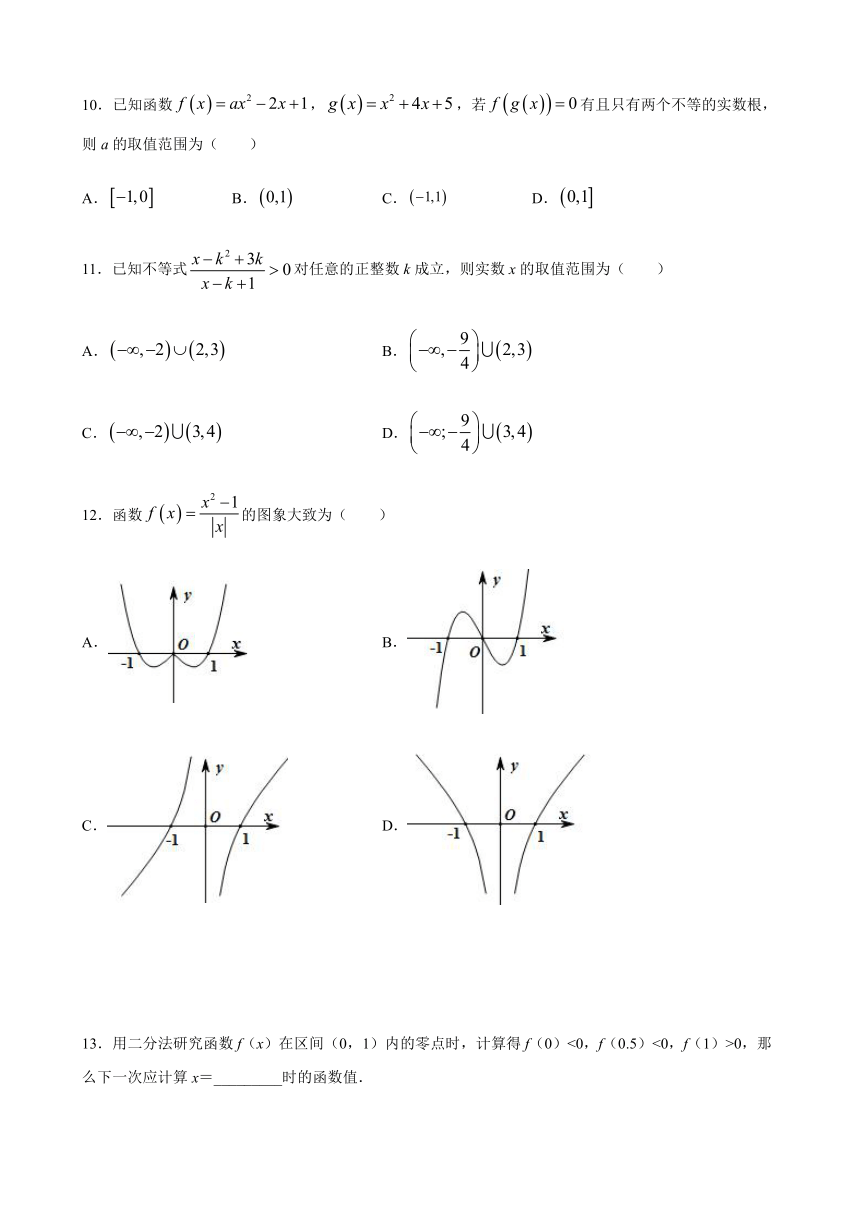


文档简介
3.3函数的应用(—)
1.某宾馆共有客床100张,各床每晚收费 10 元时可全部住满,若每晚收费每提高 2 元,便减少 10 张客床租出,则总收入 y(y>0)元与每床每晚收费应提高 x(假设 x 是 2 的正整数倍)元的关系式为( )
A.y=(10+x)(100-5x)
B.y=(10+x)(100-5x),x∈N
C.y=(10+x)(100-5x),x=2,4,6,8,…,18
D.y=(10+x)(100-5x),x=2,4,6,8
2.若函数f(x)的图象在R上连续不断,且满足f(0)<0,f(1)>0,f(2)>0,则下列说法正确的是( )
A.f(x)在区间(0,1)上一定有零点,在区间(1,2)上一定没有零点
B.f(x)在区间(0,1)上一定没有零点,在区间(1,2)上一定有零点
C.f(x)在区间(0,1)上一定有零点,在区间(1,2)上可能有零点
D.f(x)在区间(0,1)上可能有零点,在区间(1,2)上一定有零点
3.函数的零点所在区间为( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
4.若方程有两个不相等的实数根,则实数的取值范围是( )
A. B. C.,且 D.,且
5.函数f(x)=x3–9的零点所在的区间是( )
A.(–1,0) B.(0,1)
C.(1,2) D.(2,3)
6.若函数有一个零点是,那么函数的零点是( )
A., B.,
C., D.,
7.设f(x)是区间[-1,1]上连续的增函数,且,则方程f(x)=0在区间[-1,1]内( )
A.可能有3个实数根 B.可能有2个实数根
C.有唯一的实数根 D.没有实数根
8.是偶函数,则,,的大小关系为( )
A. B.
C. D.
9.某市家庭煤气的使用量和煤气费(元)满足关系 已知某家庭2019年前三个月的煤气费如下表:
月份 用气量 煤气费
一月份 4 4元
二月份 25 14元
三月份 35 19元
若四月份该家庭使用了20的煤气,则其煤气费为( )
A.11.5元 B.11元
C.10.5元 D.10元
10.已知函数,,若有且只有两个不等的实数根,则a的取值范围为( )
A. B. C. D.
11.已知不等式对任意的正整数k成立,则实数x的取值范围为( )
A. B.
C. D.
12.函数的图象大致为( )
A. B.
C. D.
13.用二分法研究函数f(x)在区间(0,1)内的零点时,计算得f(0)<0,f(0.5)<0,f(1)>0,那么下一次应计算x=_________时的函数值.
14.函数(是正实数)只有一个零点,则的最大值为_____.
15.已知a是实数,函数,若函数有且仅有两个零点,则实数a的取值范围是_______.
16.要制作一个容器为4m3,高为1m的无盖长方形容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是_______(单位:元)
17.如果定义在上的奇函数在内是减函数,又有,则的解集为________.
18.为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改,设企业的污水排放量W与时间t的关系为,用的大小评价在这段时间内企业污水治理能力的强弱,已知整改期内,甲、乙两企业的污水排放量与时间的关系如下图所示.
给出下列四个结论:
①在这段时间内,甲企业的污水治理能力比乙企业强;
②在时刻,甲企业的污水治理能力比乙企业强;
③在时刻,甲、乙两企业的污水排放都已达标;
④甲企业在这三段时间中,在的污水治理能力最强.
其中所有正确结论的序号是____________________.
19.已知函数是奇函数.
(1)求实数的值;
(2)若函数在区间上是单调增函数,求实数的取值范围;
(3)求不等式的解集.
20.已知函数.
(1)当时,求不等式的解集;
(2)若关于x的不等式的解集为R,求a的取值范围.
21.假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报04元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
22.某家用轿车的购车费9.5万元,保险费、保养费及换部分零件的费用合计每年平均4000元,每年行车里程按1万公里,前5年性能稳定,每年的油费5000元,由于磨损,从第6年开始,每年的油费以500元的速度增加,按这种标准,这种车开多少年报废比较合算?
23.函数在区间上有且只有一个零点,求实数k的取值范围.
24.已知函数是定义在上的函数,图象关于轴对称,当,.
(1)求出的解析式.
(2)若函数与函数的图象有四个交点,求的取值范围.
25.二次函数满足,且.
(1)求的解析式;
(2)若在区间上,不等式恒成立,求实数的取值范围.
26.依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为个税税额=应纳税所得额×税率-速算扣除数.应纳税所得额的计算公式为应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.其中,“基本减除费用”(免征额)为每年60000元,税率与速算扣除数见表.
级数 全年应纳税所得额所在区间 税率(%) 速算扣除数
1
3 0
2
10 2520
3
20 16920
4
25 31920
5
30 52920
6
35 85920
7
45 181920
(1)设全年应纳税所得额为t,应缴纳个税税额为y,求,并画出图象;
(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
27.某商品在近30天内每件的销售价格p(元)与时间t(天)的函数关系是该商品的日销售量Q(件)与时间t(天)的函数关系是Q=-t+40(0(1)求这种商品的日销售金额的解析式;
(2)求日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?
28.设函数在上是偶函数,在上单调递增,且,求实数的取值范围.
参考答案
1.C
【分析】四个选项的差别在于的范围不同,根据题意可选出正确的的取值范围.
【详解】依题意可知总收入的表达式为,由于是的正整数倍,且,即,故.答案为选项.
【点评】本小题主要考查简单的收入计算问题,收入等于单价乘以住的床数,根据题目写出自变量的取值范围即可得到正确选项.
2.C
【分析】根据的图像在上连续不断,,,,结合零点存在定理,判断出在区间和上零点存在的情况,得到答案.
【详解】由题知,
所以根据函数零点存在定理可得在区间上一定有零点,
又,
因此无法判断在区间上是否有零点.
故选:.
【点评】本题考查根据函数零点存在定理,判断函数零点存在的情况,属于简单题.
3.B
【分析】根据零点存在定理,结合选项,取特殊值,最后求出零点所在的区间.
【详解】由函数f(x)=x3+x–5可得f(1)=1+1–5=–3<0,f(2)=8+2–5=5>0,
故有f(1)f(2)<0,根据函数零点的判定定理可得,函数f(x)的零点所在区间为
(1,2),故选B.
【点评】本题考查了零点存在定理,考查了数学运算能力.
4.C
【分析】由题意可得,从而可求出实数的取值范围.
【详解】解:由方程有两个不相等的实数根可知,此方程为一元二次方程且判别式大于零,即可得
,解得,且.
故选:C.
【点评】本题考查了一元二次方程根的分布问题.本题的关键是由不同两根得判别式大于零.本题的易错点是忽略了这一条件.
5.D
【分析】先判断函数的单调性,然后利用零点的存在性定理判断零点所在的区间.
【详解】∵函数f(x)=x3–9在R上单调递增,f(2)=8–9=–1<0,f(3)=27–9=18>0,∴根据零点存在定理,可得函数f(x)=x3–9的零点所在的区间是(2,3),
故选D
【点评】本小题主要考查函数的单调性,考查零点的存在性定理,属于基础题.
6.C
【分析】根据题意,得到,推出,解对应的方程,即可得出结果.
【详解】因为函数有一个零点是,所以,,
所以,
由得或,
故的零点是,.
故选:C.
【点评】本题主要考查求函数零点,属于基础题型.
7.C
【分析】由函数单调性和,得出函数f(x)在区间上有唯一的零点,进而可求得答案.
【详解】由题意,函数在区间[-1,1]上是增函数,且,
∴f(x)在区间上有唯一的零点,
∴方程在区间[-1,1]内有唯一的实数根.
故选C.
【点评】本题主要考查了函数与方程的应用,其中解答中熟练应用函数零点的存在定理是解答的本题的关键,着重考查了分析问题和解答问题的能力,属于基础题.
8.B
【分析】根据偶函数的定义,确定的值和函数解析式,再根据函数的单调性和奇偶性的性质,比较大小即可.
【详解】是偶函数,
,
故,
则,;
对称轴为,开口向下,
所以在上单调递减,
,
即.
故选:B.
【点评】本题考查函数奇偶性的判断和性质,考查二次函数单调性的应用,考查推理能力与计算能力.属于较易题.
9.A
【分析】由表知一月份用气量4,煤气费4元,结合分段函数解析式可得,结合二三月份用气量及煤气费代入分段函数中求出,即可得答案.
【详解】根据一月份用气量4,煤气费4元,可知,
解得,所以所以
故选A.
【点评】本题考查利用表中数据求分段函数解析式及函数值,属于基础题.
10.B
【分析】根据选项特点使用排除法,分进行讨论,然后简单计算以及判断可得结果.
【详解】当时,,
则
所以无解,故,排除
当时,,令
则
则,不符合题意,故,排除D
故选:B
【点评】本题考查方程根的个数求解参数,对于选填,可以使用排除法、特殊值法等小技巧,使复杂问题简单化,达到解决问题的目的,属中档题.
11.A
【分析】由题意转化条件得或对任意的正整数k成立,在同一直角坐标系内作出函数与的图象,并标出取正整数的点,数形结合即可得解.
【详解】不等式对任意的正整数k成立,
或对任意的正整数k成立,
即或对任意的正整数k成立,
在同一直角坐标系内作出函数与的图象,并标出取正整数的点,如图:
数形结合可知,若要使或对任意的正整数k成立,
则.
故选:A.
【点评】本题考查了分式不等式的求解及二次函数图象的应用,考查了转化化归思想与数形结合思想,属于中档题.
12.D
【分析】分析函数的奇偶性及其在区间上的单调性,由此可得出合适的选项.
【详解】函数的定义域为,,
函数为偶函数,其图象关于轴对称,排除B、C选项;
当时,,因为,在区间上都是增函数,
所以函数在上单调递增,排除A选项,
故选:D.
【点评】函数图象的识辨可从以下方面入手:
(1)从函数的定义域,判断图象的左、右位置;从函数的值域,判断图象的上、下位置;
(2)从函数的单调性,判断图象的变化趋势;
(3)从函数的奇偶性,判断图象的对称性;
(4)从函数的特征点,排除不合要求的图象.
利用上述方法排除、筛选选项.
13.0.75
【分析】根据零点存在定理,结合已知可以确定函数零点落在的区间,结合二分法的原理,可以求出下次应计算的函数值.
【详解】∵f(0)<0,f(0.5)<0,f(1)>0,∴根据函数零点的判定定理,函数零点落在区间(0.5,1)内,取x=0.75.故答案为0.75.
【点评】本题考查了零点存在定理以及二分法的步骤,属于基础题.
14.
【分析】先由二次函数零点个数,得到,再由基本不等式,即可求出结果.
【详解】因为二次函数(是正实数)只有一个零点,
所以,即,
所以,
当且仅当时,等号成立.
故答案为:.
【点评】本题主要考查由基本不等式求积的最大值,熟记基本不等式,以及二次函数的零点个数问题即可,属于常考题型.
15.(1,+∞)
【分析】根据题意将问题转化为函数与的图象有且仅有两个交点,作出两个函数的图像,利用图像即可求解.
【详解】解析:函数有且仅有两个零点,
即函数与的图象有且仅有两个交点.
分别作出函数与的图象,如图所示,
由图易知,当时,两函数的图象有两个不同的交点,
故实数a的取值范围是(1,+∞)
故答案为:(1,+∞)
【点评】本题考查了由零点个数求参数的取值范围,考查了数形结合的思想,属于基础题.
16.160
【分析】本题根据题意建立函数关系式,再运用基本不等式求最值即可.
【详解】设该容器的总造价为元,长方体的底面矩形的长,因为无盖长方体的容积为,高为,所以长方体的底面矩形的宽为,依题意,得
故答案为:160
【点评】本题考查实际问题建立函数关系,基本不等式求最值问题,是中档题.
17.
【分析】根据题意作出函数在其定义域上的草图,由可得出或,然后利用图象可得出不等式的解集.
【详解】由题意可画出函数的草图,如图所示.
因为,所以当时,,所以;
当时,,所以.
因此,不等式的解集为.
故答案为:.
【点评】本题考查利用图象解函数不等式,解题的关键就是要结合函数的基本性质作出函数的草图,考查数形结合思想的应用,属于中等题.
18.①②③
【分析】根据定义逐一判断,即可得到结果
【详解】表示区间端点连线斜率的负数,
在这段时间内,甲的斜率比乙的小,所以甲的斜率的相反数比乙的大,因此甲企业的污水治理能力比乙企业强;①正确;
甲企业在这三段时间中,甲企业在这段时间内,甲的斜率最小,其相反数最大,即在的污水治理能力最强.④错误;
在时刻,甲切线的斜率比乙的小,所以甲切线的斜率的相反数比乙的大,甲企业的污水治理能力比乙企业强;②正确;
在时刻,甲、乙两企业的污水排放量都在污水打标排放量以下,所以都已达标;③正确;
故答案为:①②③
【点评】本题考查斜率应用、切线斜率应用、函数图象应用,考查基本分析识别能力,属中档题.
19.(1)2;(2);(3).
【分析】(1)利用,即可求出的值.
(2)画出图形,观察图像即可建立不等式求解.
(3)由可得,然后分和两种情况讨论,每种情况结合图像即可得到答案.
【详解】(1)设,则,所以,
是奇函数,,
,
(2)的图象如图
函数在区间上单调递增,
,
.
(3)由可得,即,
当时,由图像可得:,
当时,由图像可得:,
综上:
【点评】本题主要考查了分段函数的奇偶性,单调性的综合运用,属于基础题.
20.(1);(2).
【分析】(1)将代入,解二次不等式的解集即可;
(2)令即可;
【详解】解:(1)当时,,,故解集为;
(2)由题知,解得.
【点评】本题考查二次不等式的解法及二次不等式的恒成立问题,较简单.一般地,二次不等式恒成立时,利用求解.
21.选择方案三
【分析】分别计算出三种方案在第x天后所得累积回报后比较三者的大小可得正确的投资方案.
【详解】设第x天所得回报是y元,则
方案一可以用函数 进行描述;
方案二可以用函数进行描述;
方案三可以用函数进行描述.
三个模型中,第一个是常数函数,后两个都是增函数要对三个方案作出选择,
就要对它们的增长情况进行分析.
我们先用信息技术计算一下三种方案所得回报的增长情况
x 方案一 方案二 方案三
y 增加量/元 y 增加量/元 y 增加量/元
1 40 0 10 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
10 40 0 100 10 204.8 102.4
… … … … … … …
30 40 0 10 300 2147478364.8 107374182.4
再画出三个函数的图象
由表4-5-5和图4.5-7可知,方
案一的函数是常数函数,
方案二、方案三的函数都是增函数,但方案三的函数与方案二的函数的增长情况很不相同.
可以看到,尽管方案一、方案二在第1天所得回报分别是方案三的100倍和25倍,但它们的增长量固定不变,而方案三是“指数增长”,其“增长量”是成倍增加的从第7天开始,方案三比其他两个方案增长得快得多,这种增长速度是方案一方案二所无法企及的.
从每天所得回报看,在第1-3天,方案一最多;在第4天,方案一和方案二一样多,方案三最少;在第58天,方案二最多;第9天开始,方案三比其他两个方案所得回报多得多,到第30天,所得回报已超过2亿元下面再看累计的回报数.
通过信息技术列表如下
方案 天数
1 2 3 4 5 6 7 8 9 10 11
一 40 80 12 160 200 240 280 320 360 400 440
二 10 30 60 100 150 210 280 360 450 550 660
三 0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 818.8
因此,投资1-6天,应选择方案一;投资7天,应选择方案一或方案二;投资8-10天,应选择方案二;投资11天(含11天)以则应选择方案三.
【点评】本题考查一次函数模型、二次函数模型和指数函数模型在实际中的应用,注意求累计回报不太方便,可以用列表法来考虑,本题属于中档题.
22.20
【分析】设这种车开年报废比较合算,当时,总费用为,平均费用:,当,即时,取最小值.当时,平均费用:,由此得到这种车开20年报废比较合算.
【详解】设这种车开年报废比较合算,当时,总费用为:
,
平均费用:
,
当,即时,取最小值.
当时,平均费用:.
∴ 这种车开20年,平均使用费用最低,故这种车开20年报废比较合算.
【点评】本题考查函数在生产生活中的应用,考查函数的性质等基础知识,考查运算求解能力,考查化归与转化思想,是中档题.
23.
【分析】讨论三种情况,分别根据一次函数,二次函数的性质研究函数在区间上有且只有一个零点满足的条件即可求解.
【详解】当时,,函数有1个零点3,符合题意;
当时,因为
所以函数在区间上有且只有一个零点,
只需即可
即 ,
解得,
所以,
当时,函数在区间上有且只有一个零点,
只需满足,
即,
解得
综上可得或,
即实数k的取值范围为
【点评】本题主要考查了函数零点,一次函数、二次函数的性质,分类讨论的思想,属于中档题.
24.(1);(2).
【分析】(1)函数图象关于轴对称,即为偶函数,即可求出的解析式,便可得解;
(2)作出函数的图象,即可得出与函数的图象有四个交点时的取值范围.
【详解】(1)函数图象关于轴对称,即为偶函数,
当时,,
当时,,,
所以;
(2)由第一问,根据二次函数性质,作出函数图象:
要使函数与函数的图象有四个交点,则
【点评】此题考查根据函数奇偶性求函数解析式,求解函数根的个数,考查数形结合思想.
25.(1);(2).
【分析】(1)设,由得出,根据等式列关于、的方程组,解出这两个未知数,可得出函数的解析式;
(2)当时,由利用参变量分离法得出,并利用定义法证明出函数在区间上的单调性,求出函数在区间上的最小值,可求出实数的取值范围.
【详解】(1)设,则.
,
,解得,因此,;
(2)当时,由,得,得,
构造函数,,下面证明函数在区间上的单调性.
任取、,且,即,
则,
,,,,,
所以,函数在区间上单调递增,则,,
解得,因此,实数的取值范围是.
【点评】本题考查利用待定系数法求二次函数的解析式,同时也考查了利用不等式恒成立问题求参数的取值范围,在含单参数的不等式中,利用参变量分离法进行求解,可避免分类讨论,考查分析问题和解决问题的能力,属于中等题.
26.(1),图像见解析;(2)1029.6元.
【分析】(1)利用税率与速算扣除数表,根据表格中的范围,写出函数的解析式,进而可画出函数图像;
(2)根据条件求出应纳税所得额,再由的值,根据(1)计算出个税税额的值.
【详解】解:(1)根据表,可得函数的解析式为
函数图象如图所示.
(2)根据②,小王全年应纳税所得额为
,
将的值代入③,得,
所以,小王应缴纳的综合所得个税税额为1029.6元.
【点评】本题考查函数解析式的求法及应用,考查函数性质在生产生活中的实际运用等基础知识,考查运用求解能力和应用意识,是中档题.
27.(1);(2) (元),且第25天,日销售额最大
【分析】(1)设日销售金额为元,由可求出解析式,注意的取值范围;
(2)首先将函数的解析式化为二次函数的顶点式,结合二次函数的单调性即可求出函数的最值.
【详解】(1)设日销售金额为(元),则,?????
所以??.
所以.
(2)若,,则当时,(元);
若,,则
而在时单调递减,当时,(元),
由于,故时,(元),?
所以这种商品的日销售额最大值为元,且第天的日销售额最大.??
故得解.
【点评】本题主要考查二次函数的实际应用,掌握二次函数的最值和单调性是解本题的关键,属于基础题.
28.
【分析】利用偶函数的性质将所求解的不等式化为,并得出,,并利用函数在上为减函数得出,解出该不等式即可.
【详解】函数为偶函数,则,
因为在上单调递增,所以在上单调递减,
又,,
由,
得
所以,即,解得.
故答案为:.
【点评】本题考查利用偶函数与单调性的性质解函数不等式,解题时可充分利用偶函数的性质并结合该函数在区间上的单调性来求解,可简化讨论,考查分析问题和解决问题的能力,属于中等题.
1.某宾馆共有客床100张,各床每晚收费 10 元时可全部住满,若每晚收费每提高 2 元,便减少 10 张客床租出,则总收入 y(y>0)元与每床每晚收费应提高 x(假设 x 是 2 的正整数倍)元的关系式为( )
A.y=(10+x)(100-5x)
B.y=(10+x)(100-5x),x∈N
C.y=(10+x)(100-5x),x=2,4,6,8,…,18
D.y=(10+x)(100-5x),x=2,4,6,8
2.若函数f(x)的图象在R上连续不断,且满足f(0)<0,f(1)>0,f(2)>0,则下列说法正确的是( )
A.f(x)在区间(0,1)上一定有零点,在区间(1,2)上一定没有零点
B.f(x)在区间(0,1)上一定没有零点,在区间(1,2)上一定有零点
C.f(x)在区间(0,1)上一定有零点,在区间(1,2)上可能有零点
D.f(x)在区间(0,1)上可能有零点,在区间(1,2)上一定有零点
3.函数的零点所在区间为( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
4.若方程有两个不相等的实数根,则实数的取值范围是( )
A. B. C.,且 D.,且
5.函数f(x)=x3–9的零点所在的区间是( )
A.(–1,0) B.(0,1)
C.(1,2) D.(2,3)
6.若函数有一个零点是,那么函数的零点是( )
A., B.,
C., D.,
7.设f(x)是区间[-1,1]上连续的增函数,且,则方程f(x)=0在区间[-1,1]内( )
A.可能有3个实数根 B.可能有2个实数根
C.有唯一的实数根 D.没有实数根
8.是偶函数,则,,的大小关系为( )
A. B.
C. D.
9.某市家庭煤气的使用量和煤气费(元)满足关系 已知某家庭2019年前三个月的煤气费如下表:
月份 用气量 煤气费
一月份 4 4元
二月份 25 14元
三月份 35 19元
若四月份该家庭使用了20的煤气,则其煤气费为( )
A.11.5元 B.11元
C.10.5元 D.10元
10.已知函数,,若有且只有两个不等的实数根,则a的取值范围为( )
A. B. C. D.
11.已知不等式对任意的正整数k成立,则实数x的取值范围为( )
A. B.
C. D.
12.函数的图象大致为( )
A. B.
C. D.
13.用二分法研究函数f(x)在区间(0,1)内的零点时,计算得f(0)<0,f(0.5)<0,f(1)>0,那么下一次应计算x=_________时的函数值.
14.函数(是正实数)只有一个零点,则的最大值为_____.
15.已知a是实数,函数,若函数有且仅有两个零点,则实数a的取值范围是_______.
16.要制作一个容器为4m3,高为1m的无盖长方形容器,已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是_______(单位:元)
17.如果定义在上的奇函数在内是减函数,又有,则的解集为________.
18.为满足人民对美好生活的向往,环保部门要求相关企业加强污水治理,排放未达标的企业要限期整改,设企业的污水排放量W与时间t的关系为,用的大小评价在这段时间内企业污水治理能力的强弱,已知整改期内,甲、乙两企业的污水排放量与时间的关系如下图所示.
给出下列四个结论:
①在这段时间内,甲企业的污水治理能力比乙企业强;
②在时刻,甲企业的污水治理能力比乙企业强;
③在时刻,甲、乙两企业的污水排放都已达标;
④甲企业在这三段时间中,在的污水治理能力最强.
其中所有正确结论的序号是____________________.
19.已知函数是奇函数.
(1)求实数的值;
(2)若函数在区间上是单调增函数,求实数的取值范围;
(3)求不等式的解集.
20.已知函数.
(1)当时,求不等式的解集;
(2)若关于x的不等式的解集为R,求a的取值范围.
21.假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报04元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?
22.某家用轿车的购车费9.5万元,保险费、保养费及换部分零件的费用合计每年平均4000元,每年行车里程按1万公里,前5年性能稳定,每年的油费5000元,由于磨损,从第6年开始,每年的油费以500元的速度增加,按这种标准,这种车开多少年报废比较合算?
23.函数在区间上有且只有一个零点,求实数k的取值范围.
24.已知函数是定义在上的函数,图象关于轴对称,当,.
(1)求出的解析式.
(2)若函数与函数的图象有四个交点,求的取值范围.
25.二次函数满足,且.
(1)求的解析式;
(2)若在区间上,不等式恒成立,求实数的取值范围.
26.依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为个税税额=应纳税所得额×税率-速算扣除数.应纳税所得额的计算公式为应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.其中,“基本减除费用”(免征额)为每年60000元,税率与速算扣除数见表.
级数 全年应纳税所得额所在区间 税率(%) 速算扣除数
1
3 0
2
10 2520
3
20 16920
4
25 31920
5
30 52920
6
35 85920
7
45 181920
(1)设全年应纳税所得额为t,应缴纳个税税额为y,求,并画出图象;
(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
27.某商品在近30天内每件的销售价格p(元)与时间t(天)的函数关系是该商品的日销售量Q(件)与时间t(天)的函数关系是Q=-t+40(0
(2)求日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?
28.设函数在上是偶函数,在上单调递增,且,求实数的取值范围.
参考答案
1.C
【分析】四个选项的差别在于的范围不同,根据题意可选出正确的的取值范围.
【详解】依题意可知总收入的表达式为,由于是的正整数倍,且,即,故.答案为选项.
【点评】本小题主要考查简单的收入计算问题,收入等于单价乘以住的床数,根据题目写出自变量的取值范围即可得到正确选项.
2.C
【分析】根据的图像在上连续不断,,,,结合零点存在定理,判断出在区间和上零点存在的情况,得到答案.
【详解】由题知,
所以根据函数零点存在定理可得在区间上一定有零点,
又,
因此无法判断在区间上是否有零点.
故选:.
【点评】本题考查根据函数零点存在定理,判断函数零点存在的情况,属于简单题.
3.B
【分析】根据零点存在定理,结合选项,取特殊值,最后求出零点所在的区间.
【详解】由函数f(x)=x3+x–5可得f(1)=1+1–5=–3<0,f(2)=8+2–5=5>0,
故有f(1)f(2)<0,根据函数零点的判定定理可得,函数f(x)的零点所在区间为
(1,2),故选B.
【点评】本题考查了零点存在定理,考查了数学运算能力.
4.C
【分析】由题意可得,从而可求出实数的取值范围.
【详解】解:由方程有两个不相等的实数根可知,此方程为一元二次方程且判别式大于零,即可得
,解得,且.
故选:C.
【点评】本题考查了一元二次方程根的分布问题.本题的关键是由不同两根得判别式大于零.本题的易错点是忽略了这一条件.
5.D
【分析】先判断函数的单调性,然后利用零点的存在性定理判断零点所在的区间.
【详解】∵函数f(x)=x3–9在R上单调递增,f(2)=8–9=–1<0,f(3)=27–9=18>0,∴根据零点存在定理,可得函数f(x)=x3–9的零点所在的区间是(2,3),
故选D
【点评】本小题主要考查函数的单调性,考查零点的存在性定理,属于基础题.
6.C
【分析】根据题意,得到,推出,解对应的方程,即可得出结果.
【详解】因为函数有一个零点是,所以,,
所以,
由得或,
故的零点是,.
故选:C.
【点评】本题主要考查求函数零点,属于基础题型.
7.C
【分析】由函数单调性和,得出函数f(x)在区间上有唯一的零点,进而可求得答案.
【详解】由题意,函数在区间[-1,1]上是增函数,且,
∴f(x)在区间上有唯一的零点,
∴方程在区间[-1,1]内有唯一的实数根.
故选C.
【点评】本题主要考查了函数与方程的应用,其中解答中熟练应用函数零点的存在定理是解答的本题的关键,着重考查了分析问题和解答问题的能力,属于基础题.
8.B
【分析】根据偶函数的定义,确定的值和函数解析式,再根据函数的单调性和奇偶性的性质,比较大小即可.
【详解】是偶函数,
,
故,
则,;
对称轴为,开口向下,
所以在上单调递减,
,
即.
故选:B.
【点评】本题考查函数奇偶性的判断和性质,考查二次函数单调性的应用,考查推理能力与计算能力.属于较易题.
9.A
【分析】由表知一月份用气量4,煤气费4元,结合分段函数解析式可得,结合二三月份用气量及煤气费代入分段函数中求出,即可得答案.
【详解】根据一月份用气量4,煤气费4元,可知,
解得,所以所以
故选A.
【点评】本题考查利用表中数据求分段函数解析式及函数值,属于基础题.
10.B
【分析】根据选项特点使用排除法,分进行讨论,然后简单计算以及判断可得结果.
【详解】当时,,
则
所以无解,故,排除
当时,,令
则
则,不符合题意,故,排除D
故选:B
【点评】本题考查方程根的个数求解参数,对于选填,可以使用排除法、特殊值法等小技巧,使复杂问题简单化,达到解决问题的目的,属中档题.
11.A
【分析】由题意转化条件得或对任意的正整数k成立,在同一直角坐标系内作出函数与的图象,并标出取正整数的点,数形结合即可得解.
【详解】不等式对任意的正整数k成立,
或对任意的正整数k成立,
即或对任意的正整数k成立,
在同一直角坐标系内作出函数与的图象,并标出取正整数的点,如图:
数形结合可知,若要使或对任意的正整数k成立,
则.
故选:A.
【点评】本题考查了分式不等式的求解及二次函数图象的应用,考查了转化化归思想与数形结合思想,属于中档题.
12.D
【分析】分析函数的奇偶性及其在区间上的单调性,由此可得出合适的选项.
【详解】函数的定义域为,,
函数为偶函数,其图象关于轴对称,排除B、C选项;
当时,,因为,在区间上都是增函数,
所以函数在上单调递增,排除A选项,
故选:D.
【点评】函数图象的识辨可从以下方面入手:
(1)从函数的定义域,判断图象的左、右位置;从函数的值域,判断图象的上、下位置;
(2)从函数的单调性,判断图象的变化趋势;
(3)从函数的奇偶性,判断图象的对称性;
(4)从函数的特征点,排除不合要求的图象.
利用上述方法排除、筛选选项.
13.0.75
【分析】根据零点存在定理,结合已知可以确定函数零点落在的区间,结合二分法的原理,可以求出下次应计算的函数值.
【详解】∵f(0)<0,f(0.5)<0,f(1)>0,∴根据函数零点的判定定理,函数零点落在区间(0.5,1)内,取x=0.75.故答案为0.75.
【点评】本题考查了零点存在定理以及二分法的步骤,属于基础题.
14.
【分析】先由二次函数零点个数,得到,再由基本不等式,即可求出结果.
【详解】因为二次函数(是正实数)只有一个零点,
所以,即,
所以,
当且仅当时,等号成立.
故答案为:.
【点评】本题主要考查由基本不等式求积的最大值,熟记基本不等式,以及二次函数的零点个数问题即可,属于常考题型.
15.(1,+∞)
【分析】根据题意将问题转化为函数与的图象有且仅有两个交点,作出两个函数的图像,利用图像即可求解.
【详解】解析:函数有且仅有两个零点,
即函数与的图象有且仅有两个交点.
分别作出函数与的图象,如图所示,
由图易知,当时,两函数的图象有两个不同的交点,
故实数a的取值范围是(1,+∞)
故答案为:(1,+∞)
【点评】本题考查了由零点个数求参数的取值范围,考查了数形结合的思想,属于基础题.
16.160
【分析】本题根据题意建立函数关系式,再运用基本不等式求最值即可.
【详解】设该容器的总造价为元,长方体的底面矩形的长,因为无盖长方体的容积为,高为,所以长方体的底面矩形的宽为,依题意,得
故答案为:160
【点评】本题考查实际问题建立函数关系,基本不等式求最值问题,是中档题.
17.
【分析】根据题意作出函数在其定义域上的草图,由可得出或,然后利用图象可得出不等式的解集.
【详解】由题意可画出函数的草图,如图所示.
因为,所以当时,,所以;
当时,,所以.
因此,不等式的解集为.
故答案为:.
【点评】本题考查利用图象解函数不等式,解题的关键就是要结合函数的基本性质作出函数的草图,考查数形结合思想的应用,属于中等题.
18.①②③
【分析】根据定义逐一判断,即可得到结果
【详解】表示区间端点连线斜率的负数,
在这段时间内,甲的斜率比乙的小,所以甲的斜率的相反数比乙的大,因此甲企业的污水治理能力比乙企业强;①正确;
甲企业在这三段时间中,甲企业在这段时间内,甲的斜率最小,其相反数最大,即在的污水治理能力最强.④错误;
在时刻,甲切线的斜率比乙的小,所以甲切线的斜率的相反数比乙的大,甲企业的污水治理能力比乙企业强;②正确;
在时刻,甲、乙两企业的污水排放量都在污水打标排放量以下,所以都已达标;③正确;
故答案为:①②③
【点评】本题考查斜率应用、切线斜率应用、函数图象应用,考查基本分析识别能力,属中档题.
19.(1)2;(2);(3).
【分析】(1)利用,即可求出的值.
(2)画出图形,观察图像即可建立不等式求解.
(3)由可得,然后分和两种情况讨论,每种情况结合图像即可得到答案.
【详解】(1)设,则,所以,
是奇函数,,
,
(2)的图象如图
函数在区间上单调递增,
,
.
(3)由可得,即,
当时,由图像可得:,
当时,由图像可得:,
综上:
【点评】本题主要考查了分段函数的奇偶性,单调性的综合运用,属于基础题.
20.(1);(2).
【分析】(1)将代入,解二次不等式的解集即可;
(2)令即可;
【详解】解:(1)当时,,,故解集为;
(2)由题知,解得.
【点评】本题考查二次不等式的解法及二次不等式的恒成立问题,较简单.一般地,二次不等式恒成立时,利用求解.
21.选择方案三
【分析】分别计算出三种方案在第x天后所得累积回报后比较三者的大小可得正确的投资方案.
【详解】设第x天所得回报是y元,则
方案一可以用函数 进行描述;
方案二可以用函数进行描述;
方案三可以用函数进行描述.
三个模型中,第一个是常数函数,后两个都是增函数要对三个方案作出选择,
就要对它们的增长情况进行分析.
我们先用信息技术计算一下三种方案所得回报的增长情况
x 方案一 方案二 方案三
y 增加量/元 y 增加量/元 y 增加量/元
1 40 0 10 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
10 40 0 100 10 204.8 102.4
… … … … … … …
30 40 0 10 300 2147478364.8 107374182.4
再画出三个函数的图象
由表4-5-5和图4.5-7可知,方
案一的函数是常数函数,
方案二、方案三的函数都是增函数,但方案三的函数与方案二的函数的增长情况很不相同.
可以看到,尽管方案一、方案二在第1天所得回报分别是方案三的100倍和25倍,但它们的增长量固定不变,而方案三是“指数增长”,其“增长量”是成倍增加的从第7天开始,方案三比其他两个方案增长得快得多,这种增长速度是方案一方案二所无法企及的.
从每天所得回报看,在第1-3天,方案一最多;在第4天,方案一和方案二一样多,方案三最少;在第58天,方案二最多;第9天开始,方案三比其他两个方案所得回报多得多,到第30天,所得回报已超过2亿元下面再看累计的回报数.
通过信息技术列表如下
方案 天数
1 2 3 4 5 6 7 8 9 10 11
一 40 80 12 160 200 240 280 320 360 400 440
二 10 30 60 100 150 210 280 360 450 550 660
三 0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 818.8
因此,投资1-6天,应选择方案一;投资7天,应选择方案一或方案二;投资8-10天,应选择方案二;投资11天(含11天)以则应选择方案三.
【点评】本题考查一次函数模型、二次函数模型和指数函数模型在实际中的应用,注意求累计回报不太方便,可以用列表法来考虑,本题属于中档题.
22.20
【分析】设这种车开年报废比较合算,当时,总费用为,平均费用:,当,即时,取最小值.当时,平均费用:,由此得到这种车开20年报废比较合算.
【详解】设这种车开年报废比较合算,当时,总费用为:
,
平均费用:
,
当,即时,取最小值.
当时,平均费用:.
∴ 这种车开20年,平均使用费用最低,故这种车开20年报废比较合算.
【点评】本题考查函数在生产生活中的应用,考查函数的性质等基础知识,考查运算求解能力,考查化归与转化思想,是中档题.
23.
【分析】讨论三种情况,分别根据一次函数,二次函数的性质研究函数在区间上有且只有一个零点满足的条件即可求解.
【详解】当时,,函数有1个零点3,符合题意;
当时,因为
所以函数在区间上有且只有一个零点,
只需即可
即 ,
解得,
所以,
当时,函数在区间上有且只有一个零点,
只需满足,
即,
解得
综上可得或,
即实数k的取值范围为
【点评】本题主要考查了函数零点,一次函数、二次函数的性质,分类讨论的思想,属于中档题.
24.(1);(2).
【分析】(1)函数图象关于轴对称,即为偶函数,即可求出的解析式,便可得解;
(2)作出函数的图象,即可得出与函数的图象有四个交点时的取值范围.
【详解】(1)函数图象关于轴对称,即为偶函数,
当时,,
当时,,,
所以;
(2)由第一问,根据二次函数性质,作出函数图象:
要使函数与函数的图象有四个交点,则
【点评】此题考查根据函数奇偶性求函数解析式,求解函数根的个数,考查数形结合思想.
25.(1);(2).
【分析】(1)设,由得出,根据等式列关于、的方程组,解出这两个未知数,可得出函数的解析式;
(2)当时,由利用参变量分离法得出,并利用定义法证明出函数在区间上的单调性,求出函数在区间上的最小值,可求出实数的取值范围.
【详解】(1)设,则.
,
,解得,因此,;
(2)当时,由,得,得,
构造函数,,下面证明函数在区间上的单调性.
任取、,且,即,
则,
,,,,,
所以,函数在区间上单调递增,则,,
解得,因此,实数的取值范围是.
【点评】本题考查利用待定系数法求二次函数的解析式,同时也考查了利用不等式恒成立问题求参数的取值范围,在含单参数的不等式中,利用参变量分离法进行求解,可避免分类讨论,考查分析问题和解决问题的能力,属于中等题.
26.(1),图像见解析;(2)1029.6元.
【分析】(1)利用税率与速算扣除数表,根据表格中的范围,写出函数的解析式,进而可画出函数图像;
(2)根据条件求出应纳税所得额,再由的值,根据(1)计算出个税税额的值.
【详解】解:(1)根据表,可得函数的解析式为
函数图象如图所示.
(2)根据②,小王全年应纳税所得额为
,
将的值代入③,得,
所以,小王应缴纳的综合所得个税税额为1029.6元.
【点评】本题考查函数解析式的求法及应用,考查函数性质在生产生活中的实际运用等基础知识,考查运用求解能力和应用意识,是中档题.
27.(1);(2) (元),且第25天,日销售额最大
【分析】(1)设日销售金额为元,由可求出解析式,注意的取值范围;
(2)首先将函数的解析式化为二次函数的顶点式,结合二次函数的单调性即可求出函数的最值.
【详解】(1)设日销售金额为(元),则,?????
所以??.
所以.
(2)若,,则当时,(元);
若,,则
而在时单调递减,当时,(元),
由于,故时,(元),?
所以这种商品的日销售额最大值为元,且第天的日销售额最大.??
故得解.
【点评】本题主要考查二次函数的实际应用,掌握二次函数的最值和单调性是解本题的关键,属于基础题.
28.
【分析】利用偶函数的性质将所求解的不等式化为,并得出,,并利用函数在上为减函数得出,解出该不等式即可.
【详解】函数为偶函数,则,
因为在上单调递增,所以在上单调递减,
又,,
由,
得
所以,即,解得.
故答案为:.
【点评】本题考查利用偶函数与单调性的性质解函数不等式,解题时可充分利用偶函数的性质并结合该函数在区间上的单调性来求解,可简化讨论,考查分析问题和解决问题的能力,属于中等题.
