3.1.3函数的奇偶性-【新教材】人教B版(2019)高中数学必修第一册同步提高练习(Word含答案)
文档属性
| 名称 | 3.1.3函数的奇偶性-【新教材】人教B版(2019)高中数学必修第一册同步提高练习(Word含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 00:00:00 | ||
图片预览




文档简介
3.1.3函数的奇偶性
1.下列函数中,既是偶函数又存在零点的是( )
A. B. C. D.
2.若函数是奇函数,且当时,,则当时,的解析式为( )
A. B.
C. D.
3.下列函数在其定义域内既是奇函数,又是增函数的是( )
A. B. C. D.
4.下列函数中,是偶函数且在区间上是增函数的是( )
A. B.
C. D.
5.已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4等于( )
A.-6 B.6
C.-8 D.8
6.已知函数的定义域为,满足:①对任意,都有,②对任意且,都有,则函数叫“成功函数”,下列函数是“成功函数”的是( )
A. B.
C. D.
7.已知函数,则( )
A.是奇函数,且在上是增函数 B.是偶函数,且在上是增函数
C.是奇函数,且在上是减函数 D.是偶函数,且在上是减函数
8.已知函数,,若,,,则的大小关系为( )
A. B.
C. D.
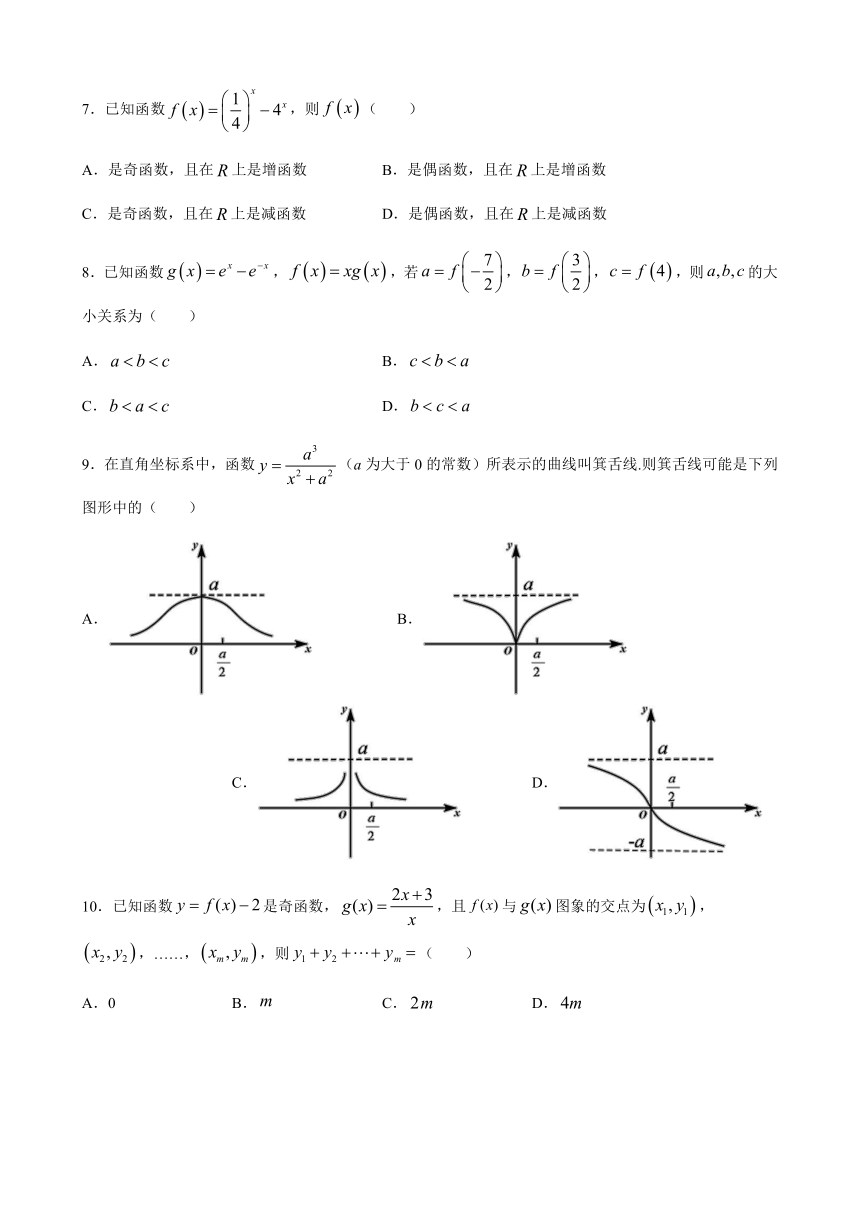
9.在直角坐标系中,函数(a为大于0的常数)所表示的曲线叫箕舌线.则箕舌线可能是下列图形中的( )
A. B. C. D.
10.已知函数是奇函数,,且与图象的交点为,,……,,则( )
A.0 B. C. D.
11.设是定义在上的奇函数,当时,为常数),则________.
12.下列几个命题:
①函数的单调减区间是;
②函数是偶函数,但不是奇函数;
③函数的值域是,则函数的值域为;
④一条曲线和直线的公共点个数是,则的值不可能是.
⑤已知在上是增函数,若,则有.
⑥若函数是一个定义在R上的函数,则函数h(x)=f(x)-f(-x)是奇函数.
⑦函数的图象可由的图象向左平移1个单位得到.
其中正确的有________________.
13.己知是上的奇函数,当时,,则_______.
14.已知函数同时满足:①对于定义域上任意,恒有;②对于定义域上的任意当时,恒有,则称函数为“理想函数”.在下列三个函数中:,,“理想函数”有______________(只填序号)
15.已知函数对任意的,都有,函数是奇函数,当时,,则方程在区间内的所有零点之和为_____________.
16.已知函数,给出下列四个命题:(1)为奇函数的充要条件是;(2)的图像关于点对称;(3)当时,方程的解集一定非空;(4)方程的解的个数一定不超过两个.其中所有正确命题的序号是__________.
17.已知函数.
(1)判断的奇偶性;
(2)若在是增函数,求实数的范围.
18.已知定义在上的函数是增函数.
(1)若,求的取值范围;
(2)若函数是奇函数,且,解不等式.
19.已知函数f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x.
(1)求出函数f(x)在R上的解析式;
(2)画出函数f(x)的图象.
20.已知是定义在上的奇函数,且.
(1)求的解析式;
(2)判断在上的单调性,并用定义加以证明.
21.已知定义在R上的函数f(x)=kx+log9(9x+1)(k∈R)
(1)若k=0,求函数f(x)的值域;
(2)若函数f(x)是偶函数,求实数k的值.
22.已知是定义在上的奇函数,当时,,
(1)求的解析式;
(2)求不等式的解集.
23.已知是定义在上的偶函数,当时,函数
(1)求当时,的解析式;
(2)当时,指出函数单调区间.
24.设函数是上的奇函数,当时,.
(1)求的表达式.
(2)求证在区间上是增函数.
25.函数是定义在上的奇函数,当时,.
(1)设,,求函数的值域;
(2)当时,若,求实数的值.
26.已知定义在上的奇函数是增函数,且.
(1)求函数的解析式;
(2)解不等式.
27.已知函数是上的奇函数,且当时,,其中.
(1)求函数的解析式;
(2)若函数的单减区间为,求不等式的解集.
28.已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图像,如图所示.
(1)请补出完整函数y=f(x)的图像;
(2)根据图像写出函数y=f(x)的增区间;
(3)根据图像写出使f(x)<0的x的取值集合.
参考答案
1.A
【分析】根据选项逐个验证,得出答案.
【详解】由于,是非奇非偶函数,是偶函数但没有零点,只有是偶函数又有零点.
故选:A.
【点评】本题主要考查函数的性质,函数的奇偶性一般利用定义进行判定,属于基础题.
2.A
【分析】考虑时,,利用已知条件求的解析式,又是奇函数,可得时的解析式.
【详解】函数是奇函数,
当时,,
时,,
,
,
.
即时,.
故选:A
【点评】本题考查了利用函数的奇偶性求解析式,意在考查灵活应用所学知识解答问题的能力,是基础题.
3.D
【分析】根据基本初等函数的单调性奇偶性,逐一分析答案四个函数在定义域上的单调性和奇偶性,逐一比照后可得答案.
【详解】解:因为函数为偶函数,所以选项不合题意;
函数在定义域上为减函数,所以选项B不合题意;
函数在定义域内不单调,所以选项C不合题意;
函数为奇函数,且,因为在上单调递增,在上单调递增,且与在处函数值都为,所以在定义域内是增函数.
故选:.
【点评】本题考查的知识点是函数的奇偶性和单调性,熟练掌握基本初等函数的单调性和奇偶性是解答的关键.属于基础题.
4.D
【分析】对选项逐一分析函数的奇偶性和单调性,由此确定正确选项.
【详解】对于A,,为反比例函数,为奇函数,且在上递减,不符合题意;
对于B,为对数函数,定义域为,是非奇非偶函数,不符合题意;
对于C,为指数函数,是非奇非偶函数,不符合题意;
对于D,为二次函数,对称轴为轴,是偶函数且在区间上是增函数,符合题意;
故选:D
【点评】本小题主要考查函数的奇偶性和单调性,属于基础题.
5.C
【分析】由奇函数f(x)满足f(x-4)=-f(x)可推出周期为8,对称轴为,画出函数大致图象,由图象分析f(x)=m的根的分布情况即可
【详解】f(x)在R上是奇函数,所以f(x-4)=-f(x)=f(-x),令得,故周期为8,即,即,函数对称轴为,画出大致图象,如图:
由图可知,两个根关于对称,两个根关于对称,设,
则,故,
故选:C
【点评】结论点睛:本题考查由函数的奇偶性,周期性,对称性求根的分布问题,常用以下结论:
(1),则的周期为;
(2),则函数的对称轴为.
6.B
【分析】根据已知可得判断“成功函数”为定义域上单调递增的奇函数,逐项判断,即可得出结论.
【详解】由任意,都有知是奇函数,
由任意且,
都有,知是增函数,
因为在定义域上是奇函数,
但在定义域上不是单增函数,故A错;
因为是奇函数,,
所以在定义域上是增函数,故B正确;
因为在定义域是减函数,
故C错;
因为在上单调递减,故D错.
故选:B.
【点评】本题考查函数的奇偶性和单调性的判断,熟练掌握初等函数单调性,以及应用导数法判断函数的单调性,属于中档题.
7.C
【分析】利用函数的单调性、奇偶性定义等方法判断函数的性质.
【详解】解:函数的定义域为,
因为,
所以为奇函数;
因为在上为减函数,在上的减函数,
所以在上的减函数,
综上:函数为奇函数,在上是减函数.
故选:C.
【点评】本题考查了函数的单调性与奇偶性的研究,解决问题的关键是熟练运用函数性质的定义.
8.C
【分析】先根据函数的奇偶性,判断函数为偶函数,再根据偶函数的性质及单调性,即可得答案;
【详解】解:依题意,有,
则为奇函数,且在上单调递增,
所以为偶函数.
当时,有,
任取,则,
由不等式的性质可得,
即,
所以函数在上递增,
因此,.
∴ ,
故选:C.
【点评】本题考查偶函数的性质及利用函数的单调性比较大小,考查逻辑推理能力、运算求解能力.
9.A
【分析】首先判断函数的奇偶性,再判断函数的单调性,最后根据特殊值即可判断;
【详解】解:因为定义域为,,故函数为偶函数,图象关于轴对称,故排除D;
又函数在上单调递增,函数在上单调递减,
根据复合函数的单调性可得函数在上单调递减,故排除B;
当时,,故排除C;
故选:A
【点评】本题考查函数图象的识别,函数的单调性与奇偶性的应用,属于中档题.
10.C
【分析】首先判断出函数的图象关于对称,然后判断出函数的图象也关于对称,由此求得的值.
【详解】令,则,则,
即,故函数的图象关于对称,又∵关于对称,
∴两个函数图象的交点都关于对称,设关于对称的两个点的纵坐标分别为,,则,
即.
故选:C
【点评】本小题主要考查函数奇偶性的应用,考查函数图象的对称性,属于中档题.
11.-3
【分析】根据函数是奇函数,求得参数,再结合已知函数解析式,求得的解析式,代值计算即可.
【详解】是定义在上的奇函数,
当时,为常数),
,
解得,
.
当时,,
,.
故答案为:
【点评】本题考查利用函数奇偶性求参数值,以及函数解析式,属综合基础题.
12.④⑤⑥
【分析】根据复合函数的单调区间的求法可判断①;根据函数奇偶性的定义可判断②;根据函数图像的平移变换可判断③;根据的图像可判断④;根据增函数的定义以及不等式的性质可判断⑤;根据奇函数的定义可判断⑥;根据函数的平移变换法则可判断⑦.
【详解】函数,则,
解得,所以函数的定义域为,所以函数的单调减区间是,故①错;
函数,定义域为,
则,函数即是偶函数也是奇函数,故②错;
函数向左平移一个单位可得,的值域是,
则的值域也是,故③错;
作出的大致图像,
由图像可知,曲线和直线的
公共点个数是,故④正确;
若,则或,因为在上是增函数,
所以,,所以,故⑤正确;
函数是一个定义在R上的函数,所以函数h(x)=f(x)-f(-x)是一个定义在R上的函数,
又,所以函数为奇函数,故⑥正确;
的图象向左平移1个单位得到,故⑦错;
故答案为:④⑤⑥
13.
【分析】由函数奇偶性,结合时函数解析式,即可求解.
【详解】由是上的奇函数,当时,,
则,
故答案为:.
【点评】本题主要考查了利用函数的奇偶性求值问题,其中熟记函数奇偶性的转化作用是解答的关键,属于基础题.
14.
【分析】根据题中条件,先判断函数是奇函数,且单调递减;再逐项判断所给函数,即可得出结果.
【详解】因为对于定义域上任意,恒有,即,
所以是奇函数;
又对于定义域上的任意当时,恒有,所以函数在定义域内单调递减;
函数的定义域为,取,,则,,此时,不满足在定义域内单调递减;排除;
由得,所以是偶函数,排除;
对于函数,根据二次函数的单调性,可得时,单调递减;时,单调递增,且,所以函数在定义域内单调递减;
又当时,,所以;
当时,,所以;
综上为奇函数;故满足题意.
故答案为:.
【点评】本题主要考查函数奇偶性的判定,以及简单函数的单调性,属于基础题型.
15.4
【分析】由已知可得函数的图象关于点对称,由可得函数的周期为2,且图象关于直线对称,从而画出函数的图像,结合图像可得出结果
【详解】∵函数是奇函数,∴函数的图象关于点对称,
∴把函数的图象向右平移1个单位可得函数的图象,
即函数的图象关于点对称,
则,
又∵,
∴,从而,
∴,即,
∴函数的周期为2,且图象关于直线对称,
画出函数的图象如图所示:
∴结合图象可得区间内有8个零点,且所有零点之和为.
故答案为:4.
【点评】此题考查函数的奇偶性和周期性,考查函数与方程,考查数形结合思想,属于中档题.
16.(1)(2)(3)
【分析】根据函数奇偶性性质,中心对称,函数零点性质,依次判断每个选项得到答案.
【详解】若函数为奇函数,则,即,
若,则,函数为奇函数,故(1)正确;
,故函数关于对称,(2)正确;
时,,即,函数的值域为,故(3)正确;
取,,则,则,,,(4)错误.
故答案为:(1)(2)(3).
【点评】本题考查了函数的奇偶性,充要条件,函数的中心对称,对应方程的解,意在考查学生的计算能力和综合应用能力.
17.(1)答案见解析;(2).
【分析】(1)分和两种情况讨论,结合函数奇偶性的定义可得出结论;
(2)任取,由可得出,进而可求得实数的取值范围.
【详解】(1)当时,函数的定义域为,,
此时,函数为偶函数;
当时,的定义域为,,
此时且,
此时,函数既不是奇函数,也不是偶函数;
(2)设,则,
,可得,,
为上的增函数,,
则,可得,,
因此,实数的取值范围是.
【点评】本题考查函数奇偶性的判定,同时也考查了利用函数在区间上的单调性求参数,考查推理能力与计算能力,属于中等题.
18.(1);(2).
【分析】(1)根据函数定义域,结合函数单调性,列出不等式组,求解即可;
(2)根据函数奇偶性得到,再利用函数单调性,结合函数定义域,即可求得不等式.
【详解】(1)由题意可得,,
求得,
即的范围是.
(2)∵函数是奇函数,且,
∴,
∵,
∴,
∴,
∴,
∴.
∴不等式的解集为.
【点评】本题考查利用函数单调性求解不等式,涉及函数奇偶性的应用,注意考虑函数定义域即可,属综合基础题.
19.(1)(2)作图见解析;
【分析】(1)根据函数为定义域为的奇函数,当时,,我们根据定义域为的奇函数的图象必过原点,且,即可求出函数在上的解析式;
(2)根据(1)中分段函数的解析式,我们易画出函数的图象.
【详解】解:(1)①当时,;
②当时,,
是奇函数,
综上:
(2)函数的图象如下图所示:
【点评】本题考查的知识点是函数奇偶性的性质及函数的图象,其中根据函数奇偶性的性质,求出函数的解析式是解答本题的关键.
20.(1) ;(2)在上单调递增,证明见解析.
【分析】(1)根据函数奇偶性,以及题中条件,求出参数,即可得出函数解析式;
(2)根据函数单调性的定义,直接证明,即可证明结论成立.
【详解】(1)∵为奇函数,∴,∴.
由,得,
∴.
(2)在上单调递增.
证明如下:
设,则
∵,∴,,∴,
∴,
∴在上单调递增.
【点评】本题主要考查由函数奇偶性求参数,以及函数单调性的证明,属于常考题型.
21.(1)(0,+∞);
(2)k.
【分析】(1)利用指数函数、对数函数的单调性进行求解即可;
(2)利用偶函数的性质进行求解即可.
【详解】(1)k=0时,,
∵9x>0,
∴9x+1>1,
∴,
∴f(x)的值域为(0,+∞);
(2)∵f(x)是偶函数,
∴f(﹣x)=f(x),
∴,
∴﹣(k+1)x=kx,
∴﹣(k+1)=k,解得k.
【点评】本题考查了指数函数、对数函数的单调性,考查了偶函数的性质,考查了数学运算能力.
22.(1);(2).
【分析】(1)根据奇函数的性质进行求解即可;
(2)根据函数的解析式分类讨论进行求解即可.
【详解】(1)∵是定义在上的奇函数,∴.
又当时,,∴.
又为奇函数,∴,∴,
∴.
(2)当时,由得,解得;
当时,无解;
当时,由得,解得.
综上,不等式的解集用区间表示为.
【点评】本题考查了奇函数的性质,考查了分类讨论思想,考查了数学运算能力.
23.(1);(2)增区间为;减区间为.
【分析】(1)利用函数奇偶性,结合的解析式,即可求得的解析式;
(2)根据二次函数的单调性,即可容易求得单调区间.
【详解】(1)设,则,
时,.
又是上的偶函数
;
(2),其对称轴为,根据其单调性可得:
函数的单调递增区间为;单调递减区间为
【点评】本题考查利用函数奇偶性求函数解析式,涉及二次函数单调区间的求解,属综合基础题.
24.(1);(2)证明见解析.
【分析】(1)先求的解析式,由,可代入求得,再由是上的奇函数,得到的解析式,从而求得的表达式;
(2)直接用定义法证明在区间上是增函数.
【详解】(1)当时,,∴.
∵是奇函数,∴,
∴,
∴
(2)设任意的,,且,则
.
∵,∴,,
∴,∴,
∴是上的增函数.
【点评】本题考查了由奇偶性求函数的解析式,定义法判断函数的单调性,属于基础题.
25.(1);(2),或,或.
【分析】(1)先由奇函数的性质求出时,,从而可得的函数解析式,然后利用二次函数的性质和奇函数的性质可求出的值域;
(2)由(1)可得时,,然后当时,令,当时,令,分别求出的值
【详解】(1)设时,则,
因为是定义在上的奇函数,且时,,
所以,即,
因为,
所以
所以当时,得关于直线对称,在上递增,在上递减,
所以,得,
当时,由奇函数关于原点对称,得.
所以的值域为;
(2)由(1)知,,
所以时,,
i)当时,令,解得或;
ii)当时,令,解得或(舍去)
综上:或或
【点评】此题考查奇函数的性质,考查二次函数的性质,考查分类讨论思想,考查计算能力,属于中档题
26.(1);(2).
【分析】(1)利用及即可确定与的值,则可得到的解析式;
(2)利用为奇函数,且在上为增函数将不等式转化为求解.
【详解】解:(1)∵是区间上的奇函数,
∴,又,
∴∴,此时,
为奇函数;
(2)∵,且为奇函数,
∴
又函数在区间上是增函数
∴,解得
故关于的不等式的解集为.
【点评】本题考查利用函数的奇偶性求参,考查利用函数的单调性与奇偶性综合求解不等式问题,难度一般,灵活转化是关键.
27.(1);(2)或.
【分析】(1)根据奇函数的定义求得时的表达式,再由可得得函数解析式;
(2)利用奇函数性质问题转化为只讨论时单调性,利用二次函数的性质可得的值,从而得函数解析式,不等式可化为或,由此可求得解集.
【详解】解:(1) 函数是定义在上的奇函数,设,则
.
又函数为奇函数,,上式即为
得
所以函数;
(2)函数的单减区间为,则在区间上单减,得的对称轴,得
∴,
由得或,即或,
解得或.∴原不等式的解集为或.
【点评】本题考查函数的奇偶性,考查求奇函数的函数解析式,解函数不等式.掌握奇函数的定义是求解析式的关键.对分段函数而言,解不等式时要注意分类讨论.
28.(1)作图见解析;(2)单调递增区间为(-1,0),(1,+∞);(3)(-2,0)∪(0,2).
【分析】(1)根据函数是偶函数补充完整函数y=f(x)的图像;
(2)根据函数的图象写出函数的单调增区间;
(3)根据图像写出使f(x)<0的x的取值集合.
【详解】(1)由题意作出函数图像如图:
(2)据图可知,单调递增区间为(-1,0),(1,+∞).
(3)据图可知,使f(x)<0的x的取值集合为(-2,0)∪(0,2).
【点评】本题主要考查函数的奇偶性的应用,考查函数的单调区间的写法,考查函数的图象的应用,意在考查学生对这些知识的理解掌握水平.
1.下列函数中,既是偶函数又存在零点的是( )
A. B. C. D.
2.若函数是奇函数,且当时,,则当时,的解析式为( )
A. B.
C. D.
3.下列函数在其定义域内既是奇函数,又是增函数的是( )
A. B. C. D.
4.下列函数中,是偶函数且在区间上是增函数的是( )
A. B.
C. D.
5.已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4等于( )
A.-6 B.6
C.-8 D.8
6.已知函数的定义域为,满足:①对任意,都有,②对任意且,都有,则函数叫“成功函数”,下列函数是“成功函数”的是( )
A. B.
C. D.
7.已知函数,则( )
A.是奇函数,且在上是增函数 B.是偶函数,且在上是增函数
C.是奇函数,且在上是减函数 D.是偶函数,且在上是减函数
8.已知函数,,若,,,则的大小关系为( )
A. B.
C. D.
9.在直角坐标系中,函数(a为大于0的常数)所表示的曲线叫箕舌线.则箕舌线可能是下列图形中的( )
A. B. C. D.
10.已知函数是奇函数,,且与图象的交点为,,……,,则( )
A.0 B. C. D.
11.设是定义在上的奇函数,当时,为常数),则________.
12.下列几个命题:
①函数的单调减区间是;
②函数是偶函数,但不是奇函数;
③函数的值域是,则函数的值域为;
④一条曲线和直线的公共点个数是,则的值不可能是.
⑤已知在上是增函数,若,则有.
⑥若函数是一个定义在R上的函数,则函数h(x)=f(x)-f(-x)是奇函数.
⑦函数的图象可由的图象向左平移1个单位得到.
其中正确的有________________.
13.己知是上的奇函数,当时,,则_______.
14.已知函数同时满足:①对于定义域上任意,恒有;②对于定义域上的任意当时,恒有,则称函数为“理想函数”.在下列三个函数中:,,“理想函数”有______________(只填序号)
15.已知函数对任意的,都有,函数是奇函数,当时,,则方程在区间内的所有零点之和为_____________.
16.已知函数,给出下列四个命题:(1)为奇函数的充要条件是;(2)的图像关于点对称;(3)当时,方程的解集一定非空;(4)方程的解的个数一定不超过两个.其中所有正确命题的序号是__________.
17.已知函数.
(1)判断的奇偶性;
(2)若在是增函数,求实数的范围.
18.已知定义在上的函数是增函数.
(1)若,求的取值范围;
(2)若函数是奇函数,且,解不等式.
19.已知函数f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x.
(1)求出函数f(x)在R上的解析式;
(2)画出函数f(x)的图象.
20.已知是定义在上的奇函数,且.
(1)求的解析式;
(2)判断在上的单调性,并用定义加以证明.
21.已知定义在R上的函数f(x)=kx+log9(9x+1)(k∈R)
(1)若k=0,求函数f(x)的值域;
(2)若函数f(x)是偶函数,求实数k的值.
22.已知是定义在上的奇函数,当时,,
(1)求的解析式;
(2)求不等式的解集.
23.已知是定义在上的偶函数,当时,函数
(1)求当时,的解析式;
(2)当时,指出函数单调区间.
24.设函数是上的奇函数,当时,.
(1)求的表达式.
(2)求证在区间上是增函数.
25.函数是定义在上的奇函数,当时,.
(1)设,,求函数的值域;
(2)当时,若,求实数的值.
26.已知定义在上的奇函数是增函数,且.
(1)求函数的解析式;
(2)解不等式.
27.已知函数是上的奇函数,且当时,,其中.
(1)求函数的解析式;
(2)若函数的单减区间为,求不等式的解集.
28.已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图像,如图所示.
(1)请补出完整函数y=f(x)的图像;
(2)根据图像写出函数y=f(x)的增区间;
(3)根据图像写出使f(x)<0的x的取值集合.
参考答案
1.A
【分析】根据选项逐个验证,得出答案.
【详解】由于,是非奇非偶函数,是偶函数但没有零点,只有是偶函数又有零点.
故选:A.
【点评】本题主要考查函数的性质,函数的奇偶性一般利用定义进行判定,属于基础题.
2.A
【分析】考虑时,,利用已知条件求的解析式,又是奇函数,可得时的解析式.
【详解】函数是奇函数,
当时,,
时,,
,
,
.
即时,.
故选:A
【点评】本题考查了利用函数的奇偶性求解析式,意在考查灵活应用所学知识解答问题的能力,是基础题.
3.D
【分析】根据基本初等函数的单调性奇偶性,逐一分析答案四个函数在定义域上的单调性和奇偶性,逐一比照后可得答案.
【详解】解:因为函数为偶函数,所以选项不合题意;
函数在定义域上为减函数,所以选项B不合题意;
函数在定义域内不单调,所以选项C不合题意;
函数为奇函数,且,因为在上单调递增,在上单调递增,且与在处函数值都为,所以在定义域内是增函数.
故选:.
【点评】本题考查的知识点是函数的奇偶性和单调性,熟练掌握基本初等函数的单调性和奇偶性是解答的关键.属于基础题.
4.D
【分析】对选项逐一分析函数的奇偶性和单调性,由此确定正确选项.
【详解】对于A,,为反比例函数,为奇函数,且在上递减,不符合题意;
对于B,为对数函数,定义域为,是非奇非偶函数,不符合题意;
对于C,为指数函数,是非奇非偶函数,不符合题意;
对于D,为二次函数,对称轴为轴,是偶函数且在区间上是增函数,符合题意;
故选:D
【点评】本小题主要考查函数的奇偶性和单调性,属于基础题.
5.C
【分析】由奇函数f(x)满足f(x-4)=-f(x)可推出周期为8,对称轴为,画出函数大致图象,由图象分析f(x)=m的根的分布情况即可
【详解】f(x)在R上是奇函数,所以f(x-4)=-f(x)=f(-x),令得,故周期为8,即,即,函数对称轴为,画出大致图象,如图:
由图可知,两个根关于对称,两个根关于对称,设,
则,故,
故选:C
【点评】结论点睛:本题考查由函数的奇偶性,周期性,对称性求根的分布问题,常用以下结论:
(1),则的周期为;
(2),则函数的对称轴为.
6.B
【分析】根据已知可得判断“成功函数”为定义域上单调递增的奇函数,逐项判断,即可得出结论.
【详解】由任意,都有知是奇函数,
由任意且,
都有,知是增函数,
因为在定义域上是奇函数,
但在定义域上不是单增函数,故A错;
因为是奇函数,,
所以在定义域上是增函数,故B正确;
因为在定义域是减函数,
故C错;
因为在上单调递减,故D错.
故选:B.
【点评】本题考查函数的奇偶性和单调性的判断,熟练掌握初等函数单调性,以及应用导数法判断函数的单调性,属于中档题.
7.C
【分析】利用函数的单调性、奇偶性定义等方法判断函数的性质.
【详解】解:函数的定义域为,
因为,
所以为奇函数;
因为在上为减函数,在上的减函数,
所以在上的减函数,
综上:函数为奇函数,在上是减函数.
故选:C.
【点评】本题考查了函数的单调性与奇偶性的研究,解决问题的关键是熟练运用函数性质的定义.
8.C
【分析】先根据函数的奇偶性,判断函数为偶函数,再根据偶函数的性质及单调性,即可得答案;
【详解】解:依题意,有,
则为奇函数,且在上单调递增,
所以为偶函数.
当时,有,
任取,则,
由不等式的性质可得,
即,
所以函数在上递增,
因此,.
∴ ,
故选:C.
【点评】本题考查偶函数的性质及利用函数的单调性比较大小,考查逻辑推理能力、运算求解能力.
9.A
【分析】首先判断函数的奇偶性,再判断函数的单调性,最后根据特殊值即可判断;
【详解】解:因为定义域为,,故函数为偶函数,图象关于轴对称,故排除D;
又函数在上单调递增,函数在上单调递减,
根据复合函数的单调性可得函数在上单调递减,故排除B;
当时,,故排除C;
故选:A
【点评】本题考查函数图象的识别,函数的单调性与奇偶性的应用,属于中档题.
10.C
【分析】首先判断出函数的图象关于对称,然后判断出函数的图象也关于对称,由此求得的值.
【详解】令,则,则,
即,故函数的图象关于对称,又∵关于对称,
∴两个函数图象的交点都关于对称,设关于对称的两个点的纵坐标分别为,,则,
即.
故选:C
【点评】本小题主要考查函数奇偶性的应用,考查函数图象的对称性,属于中档题.
11.-3
【分析】根据函数是奇函数,求得参数,再结合已知函数解析式,求得的解析式,代值计算即可.
【详解】是定义在上的奇函数,
当时,为常数),
,
解得,
.
当时,,
,.
故答案为:
【点评】本题考查利用函数奇偶性求参数值,以及函数解析式,属综合基础题.
12.④⑤⑥
【分析】根据复合函数的单调区间的求法可判断①;根据函数奇偶性的定义可判断②;根据函数图像的平移变换可判断③;根据的图像可判断④;根据增函数的定义以及不等式的性质可判断⑤;根据奇函数的定义可判断⑥;根据函数的平移变换法则可判断⑦.
【详解】函数,则,
解得,所以函数的定义域为,所以函数的单调减区间是,故①错;
函数,定义域为,
则,函数即是偶函数也是奇函数,故②错;
函数向左平移一个单位可得,的值域是,
则的值域也是,故③错;
作出的大致图像,
由图像可知,曲线和直线的
公共点个数是,故④正确;
若,则或,因为在上是增函数,
所以,,所以,故⑤正确;
函数是一个定义在R上的函数,所以函数h(x)=f(x)-f(-x)是一个定义在R上的函数,
又,所以函数为奇函数,故⑥正确;
的图象向左平移1个单位得到,故⑦错;
故答案为:④⑤⑥
13.
【分析】由函数奇偶性,结合时函数解析式,即可求解.
【详解】由是上的奇函数,当时,,
则,
故答案为:.
【点评】本题主要考查了利用函数的奇偶性求值问题,其中熟记函数奇偶性的转化作用是解答的关键,属于基础题.
14.
【分析】根据题中条件,先判断函数是奇函数,且单调递减;再逐项判断所给函数,即可得出结果.
【详解】因为对于定义域上任意,恒有,即,
所以是奇函数;
又对于定义域上的任意当时,恒有,所以函数在定义域内单调递减;
函数的定义域为,取,,则,,此时,不满足在定义域内单调递减;排除;
由得,所以是偶函数,排除;
对于函数,根据二次函数的单调性,可得时,单调递减;时,单调递增,且,所以函数在定义域内单调递减;
又当时,,所以;
当时,,所以;
综上为奇函数;故满足题意.
故答案为:.
【点评】本题主要考查函数奇偶性的判定,以及简单函数的单调性,属于基础题型.
15.4
【分析】由已知可得函数的图象关于点对称,由可得函数的周期为2,且图象关于直线对称,从而画出函数的图像,结合图像可得出结果
【详解】∵函数是奇函数,∴函数的图象关于点对称,
∴把函数的图象向右平移1个单位可得函数的图象,
即函数的图象关于点对称,
则,
又∵,
∴,从而,
∴,即,
∴函数的周期为2,且图象关于直线对称,
画出函数的图象如图所示:
∴结合图象可得区间内有8个零点,且所有零点之和为.
故答案为:4.
【点评】此题考查函数的奇偶性和周期性,考查函数与方程,考查数形结合思想,属于中档题.
16.(1)(2)(3)
【分析】根据函数奇偶性性质,中心对称,函数零点性质,依次判断每个选项得到答案.
【详解】若函数为奇函数,则,即,
若,则,函数为奇函数,故(1)正确;
,故函数关于对称,(2)正确;
时,,即,函数的值域为,故(3)正确;
取,,则,则,,,(4)错误.
故答案为:(1)(2)(3).
【点评】本题考查了函数的奇偶性,充要条件,函数的中心对称,对应方程的解,意在考查学生的计算能力和综合应用能力.
17.(1)答案见解析;(2).
【分析】(1)分和两种情况讨论,结合函数奇偶性的定义可得出结论;
(2)任取,由可得出,进而可求得实数的取值范围.
【详解】(1)当时,函数的定义域为,,
此时,函数为偶函数;
当时,的定义域为,,
此时且,
此时,函数既不是奇函数,也不是偶函数;
(2)设,则,
,可得,,
为上的增函数,,
则,可得,,
因此,实数的取值范围是.
【点评】本题考查函数奇偶性的判定,同时也考查了利用函数在区间上的单调性求参数,考查推理能力与计算能力,属于中等题.
18.(1);(2).
【分析】(1)根据函数定义域,结合函数单调性,列出不等式组,求解即可;
(2)根据函数奇偶性得到,再利用函数单调性,结合函数定义域,即可求得不等式.
【详解】(1)由题意可得,,
求得,
即的范围是.
(2)∵函数是奇函数,且,
∴,
∵,
∴,
∴,
∴,
∴.
∴不等式的解集为.
【点评】本题考查利用函数单调性求解不等式,涉及函数奇偶性的应用,注意考虑函数定义域即可,属综合基础题.
19.(1)(2)作图见解析;
【分析】(1)根据函数为定义域为的奇函数,当时,,我们根据定义域为的奇函数的图象必过原点,且,即可求出函数在上的解析式;
(2)根据(1)中分段函数的解析式,我们易画出函数的图象.
【详解】解:(1)①当时,;
②当时,,
是奇函数,
综上:
(2)函数的图象如下图所示:
【点评】本题考查的知识点是函数奇偶性的性质及函数的图象,其中根据函数奇偶性的性质,求出函数的解析式是解答本题的关键.
20.(1) ;(2)在上单调递增,证明见解析.
【分析】(1)根据函数奇偶性,以及题中条件,求出参数,即可得出函数解析式;
(2)根据函数单调性的定义,直接证明,即可证明结论成立.
【详解】(1)∵为奇函数,∴,∴.
由,得,
∴.
(2)在上单调递增.
证明如下:
设,则
∵,∴,,∴,
∴,
∴在上单调递增.
【点评】本题主要考查由函数奇偶性求参数,以及函数单调性的证明,属于常考题型.
21.(1)(0,+∞);
(2)k.
【分析】(1)利用指数函数、对数函数的单调性进行求解即可;
(2)利用偶函数的性质进行求解即可.
【详解】(1)k=0时,,
∵9x>0,
∴9x+1>1,
∴,
∴f(x)的值域为(0,+∞);
(2)∵f(x)是偶函数,
∴f(﹣x)=f(x),
∴,
∴﹣(k+1)x=kx,
∴﹣(k+1)=k,解得k.
【点评】本题考查了指数函数、对数函数的单调性,考查了偶函数的性质,考查了数学运算能力.
22.(1);(2).
【分析】(1)根据奇函数的性质进行求解即可;
(2)根据函数的解析式分类讨论进行求解即可.
【详解】(1)∵是定义在上的奇函数,∴.
又当时,,∴.
又为奇函数,∴,∴,
∴.
(2)当时,由得,解得;
当时,无解;
当时,由得,解得.
综上,不等式的解集用区间表示为.
【点评】本题考查了奇函数的性质,考查了分类讨论思想,考查了数学运算能力.
23.(1);(2)增区间为;减区间为.
【分析】(1)利用函数奇偶性,结合的解析式,即可求得的解析式;
(2)根据二次函数的单调性,即可容易求得单调区间.
【详解】(1)设,则,
时,.
又是上的偶函数
;
(2),其对称轴为,根据其单调性可得:
函数的单调递增区间为;单调递减区间为
【点评】本题考查利用函数奇偶性求函数解析式,涉及二次函数单调区间的求解,属综合基础题.
24.(1);(2)证明见解析.
【分析】(1)先求的解析式,由,可代入求得,再由是上的奇函数,得到的解析式,从而求得的表达式;
(2)直接用定义法证明在区间上是增函数.
【详解】(1)当时,,∴.
∵是奇函数,∴,
∴,
∴
(2)设任意的,,且,则
.
∵,∴,,
∴,∴,
∴是上的增函数.
【点评】本题考查了由奇偶性求函数的解析式,定义法判断函数的单调性,属于基础题.
25.(1);(2),或,或.
【分析】(1)先由奇函数的性质求出时,,从而可得的函数解析式,然后利用二次函数的性质和奇函数的性质可求出的值域;
(2)由(1)可得时,,然后当时,令,当时,令,分别求出的值
【详解】(1)设时,则,
因为是定义在上的奇函数,且时,,
所以,即,
因为,
所以
所以当时,得关于直线对称,在上递增,在上递减,
所以,得,
当时,由奇函数关于原点对称,得.
所以的值域为;
(2)由(1)知,,
所以时,,
i)当时,令,解得或;
ii)当时,令,解得或(舍去)
综上:或或
【点评】此题考查奇函数的性质,考查二次函数的性质,考查分类讨论思想,考查计算能力,属于中档题
26.(1);(2).
【分析】(1)利用及即可确定与的值,则可得到的解析式;
(2)利用为奇函数,且在上为增函数将不等式转化为求解.
【详解】解:(1)∵是区间上的奇函数,
∴,又,
∴∴,此时,
为奇函数;
(2)∵,且为奇函数,
∴
又函数在区间上是增函数
∴,解得
故关于的不等式的解集为.
【点评】本题考查利用函数的奇偶性求参,考查利用函数的单调性与奇偶性综合求解不等式问题,难度一般,灵活转化是关键.
27.(1);(2)或.
【分析】(1)根据奇函数的定义求得时的表达式,再由可得得函数解析式;
(2)利用奇函数性质问题转化为只讨论时单调性,利用二次函数的性质可得的值,从而得函数解析式,不等式可化为或,由此可求得解集.
【详解】解:(1) 函数是定义在上的奇函数,设,则
.
又函数为奇函数,,上式即为
得
所以函数;
(2)函数的单减区间为,则在区间上单减,得的对称轴,得
∴,
由得或,即或,
解得或.∴原不等式的解集为或.
【点评】本题考查函数的奇偶性,考查求奇函数的函数解析式,解函数不等式.掌握奇函数的定义是求解析式的关键.对分段函数而言,解不等式时要注意分类讨论.
28.(1)作图见解析;(2)单调递增区间为(-1,0),(1,+∞);(3)(-2,0)∪(0,2).
【分析】(1)根据函数是偶函数补充完整函数y=f(x)的图像;
(2)根据函数的图象写出函数的单调增区间;
(3)根据图像写出使f(x)<0的x的取值集合.
【详解】(1)由题意作出函数图像如图:
(2)据图可知,单调递增区间为(-1,0),(1,+∞).
(3)据图可知,使f(x)<0的x的取值集合为(-2,0)∪(0,2).
【点评】本题主要考查函数的奇偶性的应用,考查函数的单调区间的写法,考查函数的图象的应用,意在考查学生对这些知识的理解掌握水平.
