第一章 三角形专项训练:全等三角形的判定与性质 (含答案)
文档属性
| 名称 | 第一章 三角形专项训练:全等三角形的判定与性质 (含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专项训练
全等三角形的判定与性质
类型一 网格中的全等三角形
1.如图所示,网格中有△ABC及线段DE,在网格上找一点F(必须在格点上),使△DEF与△ABC全等,则这样的点有( )
A.1个 B.2个 C.3个 D.4个
类型二 寻求判定三角形全等的条件
2.如图所示,已知AC=DB,添加下列四个条件:①∠A=∠D;②∠ABD=∠DCA;③∠ACB=∠DBC;④∠ABC=∠DCB中的一个,其中能使△ABC≌△DCB的有( )
A.1个 B.2个 C.3个 D.4个
3.如图所示,在△ABC和△ABD中,已知∠CAB=∠DAB,在不添加任何辅助线的前提下,要使△ABC≌△ABD,再添加的一个条件不可以是( )
A.AC=AD B.BC=BD C.∠C=∠D D.∠CBE=∠DBE
4.如图所示,在△ABO与△CDO中,AB=CD,请你补充一个条件,使△ABO≌△CDO.你补充的条件是________________.
类型三 证明两三角形全等
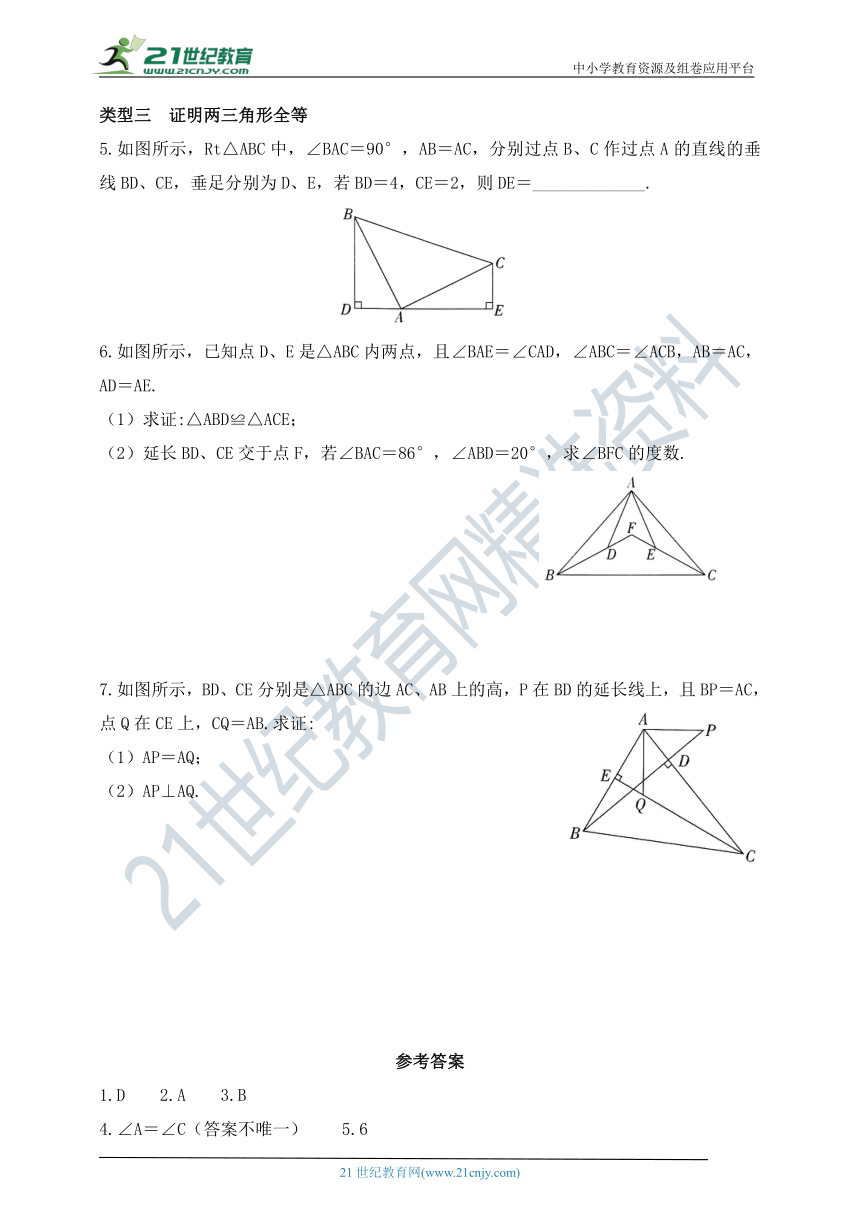
5.如图所示,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的直线的垂线BD、CE,垂足分别为D、E,若BD=4,CE=2,则DE=_____________.
6.如图所示,已知点D、E是△ABC内两点,且∠BAE=∠CAD,∠ABC=∠ACB,AB=AC,AD=AE.
(1)求证:△ABD≌△ACE;
(2)延长BD、CE交于点F,若∠BAC=86°,∠ABD=20°,求∠BFC的度数.
7.如图所示,BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB.求证:
(1)AP=AQ;
(2)AP⊥AQ.
参考答案
1.D 2.A 3.B
4.∠A=∠C(答案不唯一) 5.6
6.解析 (1)证明:∵∠BAE=∠CAD,∴∠BAD=∠CAE,
在△ABD和△ACE中,∴△ABD≌△ACE(SAS).
(2)∵△ABD≌△ACE,∴∠ACE=∠ABD=20°,
∵∠ABC=∠ACB=×(180°-86°)=47°,
∴∠FBC=∠FCB=47°-20°=27°,
∴∠BFC=180°-27°-27°=126°.
7.证明(1)∵BD、CE分别是△ABC的边AC、AB上的高,
∴BD⊥AC,CE⊥AB,∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAC=90°,∠ACE+∠BAC=90°,∴∠ABD=∠ACE,
在△ABP和△QCA中,
∴△ABP≌△QCA(SAS),∴AP=AQ.
(2)由(1)知△ABP≌△QCA,∴∠P=∠CAQ,
∵BD⊥AC,∴∠P+∠CAP=90°,
∴∠CAQ+∠CAP=90°,即∠QAP=90°,∴AP⊥AQ.
_21?????????è?????(www.21cnjy.com)_
专项训练
全等三角形的判定与性质
类型一 网格中的全等三角形
1.如图所示,网格中有△ABC及线段DE,在网格上找一点F(必须在格点上),使△DEF与△ABC全等,则这样的点有( )
A.1个 B.2个 C.3个 D.4个
类型二 寻求判定三角形全等的条件
2.如图所示,已知AC=DB,添加下列四个条件:①∠A=∠D;②∠ABD=∠DCA;③∠ACB=∠DBC;④∠ABC=∠DCB中的一个,其中能使△ABC≌△DCB的有( )
A.1个 B.2个 C.3个 D.4个
3.如图所示,在△ABC和△ABD中,已知∠CAB=∠DAB,在不添加任何辅助线的前提下,要使△ABC≌△ABD,再添加的一个条件不可以是( )
A.AC=AD B.BC=BD C.∠C=∠D D.∠CBE=∠DBE
4.如图所示,在△ABO与△CDO中,AB=CD,请你补充一个条件,使△ABO≌△CDO.你补充的条件是________________.
类型三 证明两三角形全等
5.如图所示,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的直线的垂线BD、CE,垂足分别为D、E,若BD=4,CE=2,则DE=_____________.
6.如图所示,已知点D、E是△ABC内两点,且∠BAE=∠CAD,∠ABC=∠ACB,AB=AC,AD=AE.
(1)求证:△ABD≌△ACE;
(2)延长BD、CE交于点F,若∠BAC=86°,∠ABD=20°,求∠BFC的度数.
7.如图所示,BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB.求证:
(1)AP=AQ;
(2)AP⊥AQ.
参考答案
1.D 2.A 3.B
4.∠A=∠C(答案不唯一) 5.6
6.解析 (1)证明:∵∠BAE=∠CAD,∴∠BAD=∠CAE,
在△ABD和△ACE中,∴△ABD≌△ACE(SAS).
(2)∵△ABD≌△ACE,∴∠ACE=∠ABD=20°,
∵∠ABC=∠ACB=×(180°-86°)=47°,
∴∠FBC=∠FCB=47°-20°=27°,
∴∠BFC=180°-27°-27°=126°.
7.证明(1)∵BD、CE分别是△ABC的边AC、AB上的高,
∴BD⊥AC,CE⊥AB,∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAC=90°,∠ACE+∠BAC=90°,∴∠ABD=∠ACE,
在△ABP和△QCA中,
∴△ABP≌△QCA(SAS),∴AP=AQ.
(2)由(1)知△ABP≌△QCA,∴∠P=∠CAQ,
∵BD⊥AC,∴∠P+∠CAP=90°,
∴∠CAQ+∠CAP=90°,即∠QAP=90°,∴AP⊥AQ.
_21?????????è?????(www.21cnjy.com)_
