小学数学 五年级上册数学课件 梯形的面积人教版 (48张PPT)
文档属性
| 名称 | 小学数学 五年级上册数学课件 梯形的面积人教版 (48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 00:00:00 | ||
图片预览





文档简介
(共46张PPT)
梯形的面积
教学目标
在探索过程中,通过观察、操作、比较等活动,运用分割、
拼摆的方法推导出梯形的面积计算公式.
掌握梯形的面积计算公式,能运用梯形的面积计算公式解
决有关梯形面积的实际问题.
培养观察、分析、概括获得积极的情感体验,培养学习数
学的兴趣.
教学重点
教学难点
掌握梯形面积的计算公式,会利用公式解决实际问题.
理解梯形面积公式推导的多种方法,体会转化的思想.
请同学们和老师一起回忆以前学过的平面图形
长方形
正方形
三角形
平行四边形
梯形
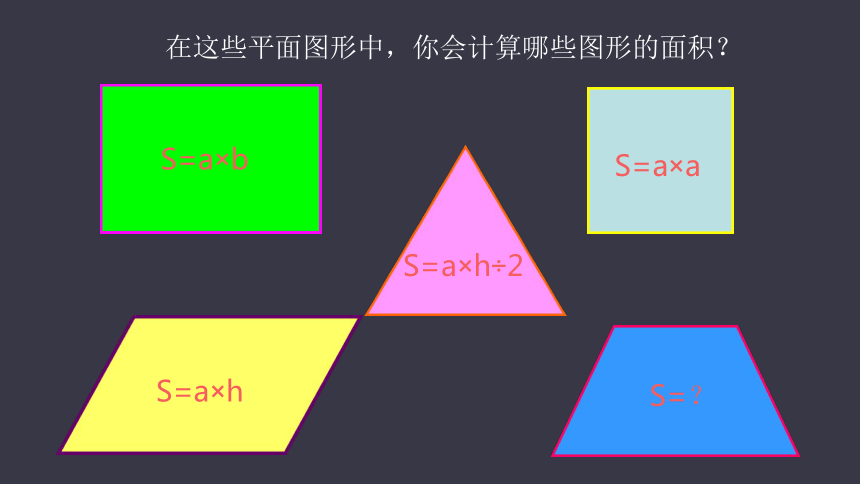
在这些平面图形中,你会计算哪些图形的面积?
S=a×b
S=a×h÷2
S=a×a
S=a×h
S=?
车窗玻璃的形状
是梯形!怎样求
出它的面积呢?
这节课我们就来一起学习梯形的面积.
问题:回忆一下,我们是怎样推导出三角形面积的计算公式的?
你能用学过的方法推导出梯形的面积计算公式吗?
思考问题
1、你能不能用已经学过的本领想办法求出梯形的面积?
2、你如果想不出办法,可以通过操作手中的学具想一种求梯形
面积的办法?
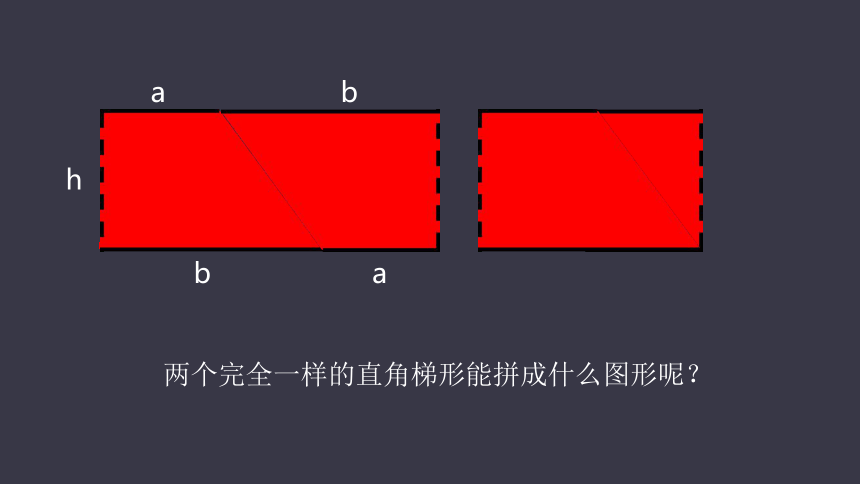
两个完全一样的直角梯形能拼成什么图形呢?
a
b
h
a
b
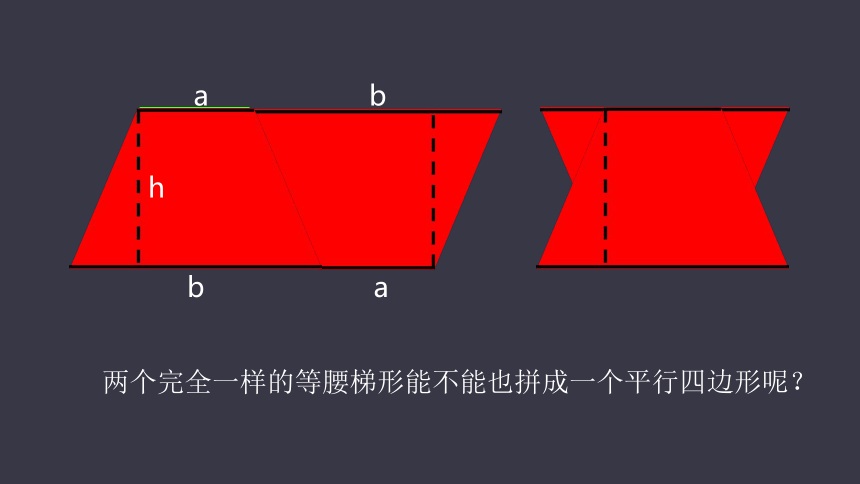
两个完全一样的等腰梯形能不能也拼成一个平行四边形呢?
a
b
h
a
b
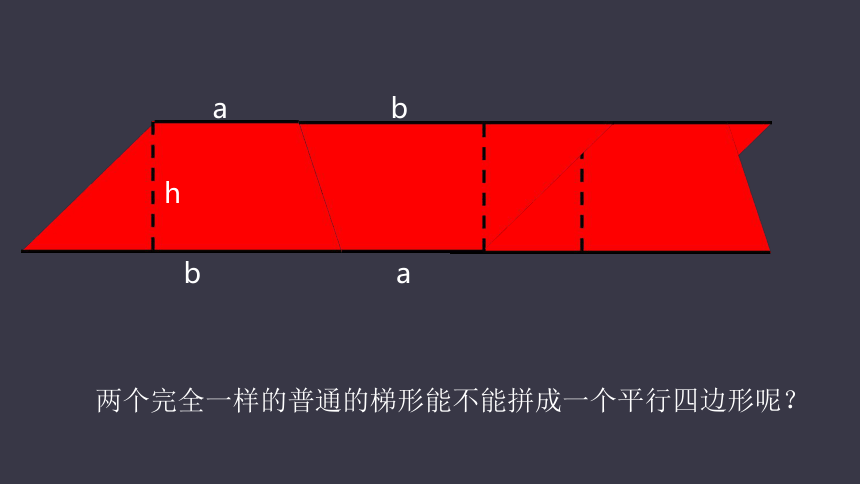
两个完全一样的普通的梯形能不能拼成一个平行四边形呢?
a
b
h
a
b
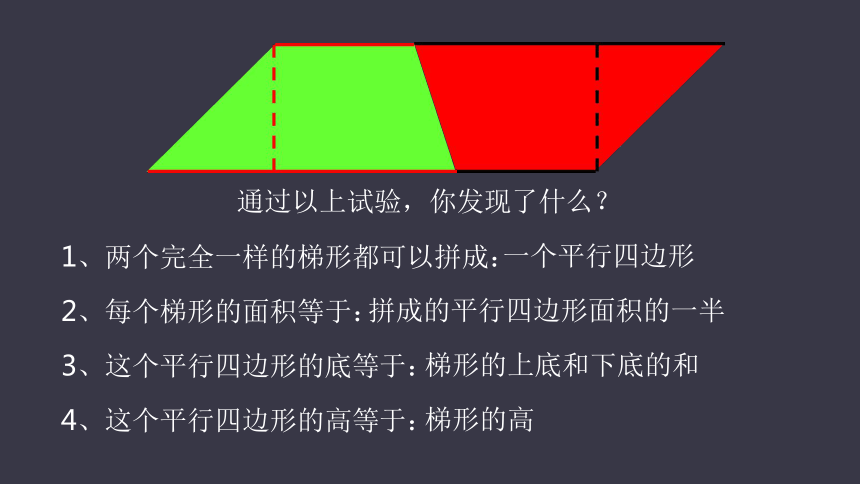
通过以上试验,你发现了什么?
1、两个完全一样的梯形都可以拼成:
一个平行四边形
2、每个梯形的面积等于:
拼成的平行四边形面积的一半
3、这个平行四边形的底等于:
梯形的上底和下底的和
4、这个平行四边形的高等于:
梯形的高
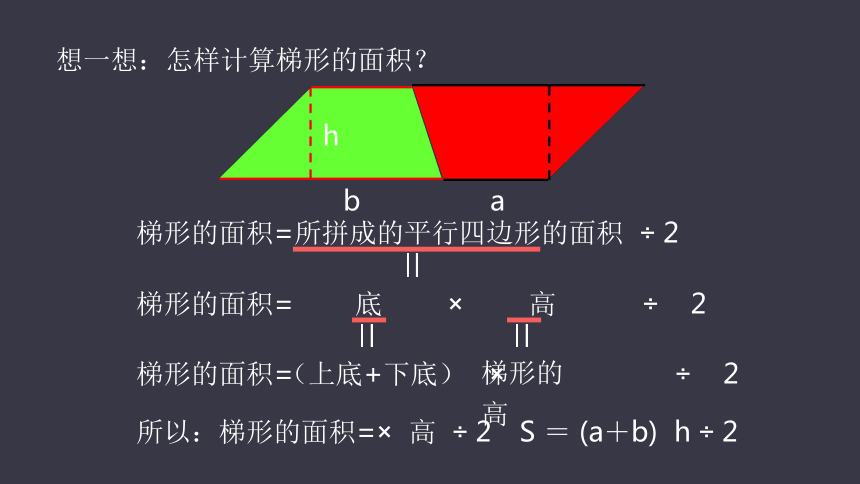
想一想:怎样计算梯形的面积?
梯形的面积=所拼成的平行四边形的面积 ÷ 2
梯形的面积= × ÷ 2
梯形的面积= ÷ 2
所以:梯形的面积=× 高 ÷ 2
S = (a+b) h ÷ 2
a
b
h
底 × 高
(上底+下底)
梯形的高
想一想:这样分开,可以计算梯形的面积吗
a
b
h
a
b
h
S = ah + (b-a) h÷2
S = bh÷2 + ah÷2
与S=(a+b)h÷2比较,这三种计算方法,你更喜欢哪一种?
这样分割可不可以?
S = (a+b) ( h ÷ 2)
你还有其他方法推导出梯形面积的计算公式吗?
把一个梯形分割成一个三角形和一个平行四边形
因为:一个三角形的面积 +一个平行四边形的面积是:
2×4÷2+3×4
=(2÷2+3)×4
=(2+3+3)×4÷2
=(3 + 5)×4÷2
所以:梯形的面积 (3+5)×4÷2
3厘米
5厘米
4厘米
(一)借助拼摆,自主探究
1. 出示情境:老师为每个小组都准备了学具,请同学们先打开学具袋看看都有什么。(每个小组的梯形互不相同)
(一)借助拼摆,自主探究
2. 提出问题:你能根据已有的经验,借助手中的学具推导出梯形的面积计算公式吗?
3. 提出要求:请同学们两人一组,借助你们手中的梯形纸片,可以拼一 拼,画一画,剪一剪,看看能不能把梯形转化成我们学习过的图形,并找到转化前后图形间的联系,把你找到的联系在纸上写一写,让别 人一眼就能看出你是如何推导出梯形面积计算方法的,看哪组的方法最多,学具不够用可以找老师领取。
4. 学生自主探究,教师巡视搜集资源。
(一)借助拼摆,自主探究
5. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?
预设一:
平行四边形的面积= 底 × 高
梯形的面积=(上底+下底)×高÷2
2个梯形的面积 (上底+下底) 高
(一)借助拼摆,自主探究
5. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?
预设二:
平行四边形的面积= 底 × 高
梯形的面积=(上底+下底)×高÷2
2个梯形的面积 (上底+下底) 高
(一)借助拼摆,自主探究
6. 总结概括,提升认识:通过同学们刚才的汇报,我们发现只要是两个完全一样的梯形,我们就能把它们拼成一个平行四边形或长方形,充分论证了梯形的面积=(上底+下底)×高÷2。
过渡:刚才我还发现有的同学只用一个梯形就推导出了梯形的面积计算公式,你们想看看吗?
(一)借助拼摆,自主探究
预设一:
7. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?
梯形的面积=小三角形的面积+大三角形的面积
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
(一)借助拼摆,自主探究
预设二:
7. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?
=(上底+下底)×高÷2
梯形的面积=平行四边形的面积+三角形的面积
=上底×高+(下底-上底)×高÷2
(一)借助拼摆,自主探究
预设四:
7. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?
平行四边形的面积= 底 × 高
梯形的面积 (上底+下底)÷2 高
梯形的面积=(上底+下底)×高÷2
(一)借助拼摆,自主探究
8. 总结概括,提升认识:通过同学们刚才的汇报,我们发现只要是运用相应的方法把梯形分割或割补成学过的图形,然后找到相应的新旧图形的联系,充分论证了梯形的面积=(上底+下底)×高÷2。
9. 如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式是: S=(a+b)h÷2
s=(a+b)h÷2
=(36+120)×135÷2
= 156×135÷2
答:这个梯形的面积是10530平方米。
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
S =(a+b)h÷2
=(40+71)×40÷2
=111×40÷2
S =(a+b)h÷2
=(45+65)×40÷2
=110×40÷2
1.两个完全一样的梯形可以拼成一个平行四边形,这个平行四边形的底等于梯形的( )与( )的和,高等于梯形的( ),每个梯形的面积等于拼成的平行 四边形面积的( )。
提高练习
2.一个梯形的上底是12米,下底是8米,高是4米,面积是( )平方米。
上底
下 底
高
一半
4 0
判断
1、梯形的面积公式用字母表示是:S=(a+b)h
梯形的面积公式用字母表示是:S=(a+b)h÷2
2、两个梯形的高相等,它们的面积就相等。
3、两个面积相等梯形可以拼成一个平行四边形。
两个完全一样的梯形可以拼成一个平行四边形。
4、两个面积相等的梯形一定能拼成一个平行四边形。 ( )
5、平行四边形的面积一定比梯形的面积大。( )
6、一个平行四边形可以分成两个梯形 。 ( )
寻找合适的条件,求出图中阴影梯形的面积
S=(a+b)h÷2
=(18+12) × 9÷2
=30 × 9÷2
=135(平方厘米)
7-4=3(厘米)
S=(a+b)h÷2
=(7+3) × 5÷2
=10 × 5÷2
=25(平方厘米)
8-2-1=5(厘米)
S=(a+b)h÷2
= (5+8) ×4÷2
=13 × 4÷2
=26(平方厘米)
1、用篱笆围成一个梯形养鸡场(如图),其中一边利用房屋墙壁。已知篱笆长80m,求养鸡场的占地面积。
提示:靠墙的一边不用围篱笆。有两个直角,20m相当于梯形的高,那么46m减去20m,剩下的是什么?
(46-20)×20÷2
=26×20÷2
=520÷2
一条新挖的水渠,横截面是梯形(如图),渠口宽2.8m,渠底宽1.4m,渠深1.2m。它的横向横截面的面积是多少平方米?
(2.8+1.4)×1.2÷2
=4.2×1.2÷2
=5.04÷2
=2.52 ( 平方米 )
答:它的横截面积是2.52平方米。
已知一个梯形的上底、下底和面积,求高是多少?
10m
20m
解:设高是x米。
(25+10)x÷2=140
35x÷2=140
35x÷2×2=140×2
35x=280
35x÷35=280÷35
x=8
答:高是8米。
还有没有其它的方法?
140×2÷(25+10)
=140×2÷35
=280÷35
=8(米)
答:高是8米。
练习二十一
1.一条新挖的水渠,横截面是梯形。渠口宽2.8m,渠底宽1.4m,渠深1.2m。横截面的面积是多少平方米?
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
答:横截面的面积是10530平方米。
练习二十一
2. 计算下面每个梯形的面积。
S =(a+b)h÷2
=(3+4)×5÷2
=12×5÷2
S =(a+b)h÷2
=(8.2+5.9)×4.8÷2
=14.1×4.8÷2
S =(a+b)h÷2
=(12+15)×20÷2
=27×20÷2
练习二十一
3.自己想办法求出这两个梯形的面积。
练习二十一
4.科技小组制作飞机模型,机翼的平面图是由两个完全相同的梯形组成的,机翼的面积是多少?
S=(a+b)h÷2
=(48+100)×250÷2
=148×250÷2
练习二十一
5.寻找合适的条件,求出下图中涂色梯形的面积。(单位:cm)
S =(a+b)h÷2
=(12+18)×6÷2
=30×6÷2
S =(a+b)h÷2
=(5-2.3+5)×3.4÷2
=7.7×3.4÷2
S =(a+b)h÷2
=(7.2-2.2-1.6 +7.2)×4.8÷2
=10.6×4.8÷2
练习二十一
6. 靠墙边围成一个花坛,围花坛的篱笆长46m,求这个花坛的面积。
这个梯形的上底和下底和:
46-20 =26(m)
S=(a+b)h÷2
=26×20÷2
练习二十一
解:设下底是x厘米
(4.5+x)×3÷2=15
(4.5+x)×3=15×2
(4.5+x)×3=30
(4.5+x)=30÷3
4.5+x=10
x=10 -4.5
x=5.5
答:下底是5.5厘米。
练习二十一
8.我们经常见到圆木、钢管等堆成像下图的形状。通常采用下面的方法求总根数:
(2+6)×5÷2
=8×5÷2
=20(根)
答:圆木的总根数是20根。
练习二十一
9. 在周围找一个梯形,量出它的底和高,再算出它的面积。
练习二十一
S=(a+b)h÷2
=(160+180)×50÷2
=340×50÷2
8500÷10=850(棵)
答:这个果园共有果树850棵。
练习二十一
11.在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少?有几种求法?
剩下的是一个三角形
(3.5-2)×1.8÷2
=1.5×1.8÷2
答:剩下的面积是1.35平方厘米。
=1.35(平方厘米)
梯形的面积
教学目标
在探索过程中,通过观察、操作、比较等活动,运用分割、
拼摆的方法推导出梯形的面积计算公式.
掌握梯形的面积计算公式,能运用梯形的面积计算公式解
决有关梯形面积的实际问题.
培养观察、分析、概括获得积极的情感体验,培养学习数
学的兴趣.
教学重点
教学难点
掌握梯形面积的计算公式,会利用公式解决实际问题.
理解梯形面积公式推导的多种方法,体会转化的思想.
请同学们和老师一起回忆以前学过的平面图形
长方形
正方形
三角形
平行四边形
梯形
在这些平面图形中,你会计算哪些图形的面积?
S=a×b
S=a×h÷2
S=a×a
S=a×h
S=?
车窗玻璃的形状
是梯形!怎样求
出它的面积呢?
这节课我们就来一起学习梯形的面积.
问题:回忆一下,我们是怎样推导出三角形面积的计算公式的?
你能用学过的方法推导出梯形的面积计算公式吗?
思考问题
1、你能不能用已经学过的本领想办法求出梯形的面积?
2、你如果想不出办法,可以通过操作手中的学具想一种求梯形
面积的办法?
两个完全一样的直角梯形能拼成什么图形呢?
a
b
h
a
b
两个完全一样的等腰梯形能不能也拼成一个平行四边形呢?
a
b
h
a
b
两个完全一样的普通的梯形能不能拼成一个平行四边形呢?
a
b
h
a
b
通过以上试验,你发现了什么?
1、两个完全一样的梯形都可以拼成:
一个平行四边形
2、每个梯形的面积等于:
拼成的平行四边形面积的一半
3、这个平行四边形的底等于:
梯形的上底和下底的和
4、这个平行四边形的高等于:
梯形的高
想一想:怎样计算梯形的面积?
梯形的面积=所拼成的平行四边形的面积 ÷ 2
梯形的面积= × ÷ 2
梯形的面积= ÷ 2
所以:梯形的面积=× 高 ÷ 2
S = (a+b) h ÷ 2
a
b
h
底 × 高
(上底+下底)
梯形的高
想一想:这样分开,可以计算梯形的面积吗
a
b
h
a
b
h
S = ah + (b-a) h÷2
S = bh÷2 + ah÷2
与S=(a+b)h÷2比较,这三种计算方法,你更喜欢哪一种?
这样分割可不可以?
S = (a+b) ( h ÷ 2)
你还有其他方法推导出梯形面积的计算公式吗?
把一个梯形分割成一个三角形和一个平行四边形
因为:一个三角形的面积 +一个平行四边形的面积是:
2×4÷2+3×4
=(2÷2+3)×4
=(2+3+3)×4÷2
=(3 + 5)×4÷2
所以:梯形的面积 (3+5)×4÷2
3厘米
5厘米
4厘米
(一)借助拼摆,自主探究
1. 出示情境:老师为每个小组都准备了学具,请同学们先打开学具袋看看都有什么。(每个小组的梯形互不相同)
(一)借助拼摆,自主探究
2. 提出问题:你能根据已有的经验,借助手中的学具推导出梯形的面积计算公式吗?
3. 提出要求:请同学们两人一组,借助你们手中的梯形纸片,可以拼一 拼,画一画,剪一剪,看看能不能把梯形转化成我们学习过的图形,并找到转化前后图形间的联系,把你找到的联系在纸上写一写,让别 人一眼就能看出你是如何推导出梯形面积计算方法的,看哪组的方法最多,学具不够用可以找老师领取。
4. 学生自主探究,教师巡视搜集资源。
(一)借助拼摆,自主探究
5. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?
预设一:
平行四边形的面积= 底 × 高
梯形的面积=(上底+下底)×高÷2
2个梯形的面积 (上底+下底) 高
(一)借助拼摆,自主探究
5. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?
预设二:
平行四边形的面积= 底 × 高
梯形的面积=(上底+下底)×高÷2
2个梯形的面积 (上底+下底) 高
(一)借助拼摆,自主探究
6. 总结概括,提升认识:通过同学们刚才的汇报,我们发现只要是两个完全一样的梯形,我们就能把它们拼成一个平行四边形或长方形,充分论证了梯形的面积=(上底+下底)×高÷2。
过渡:刚才我还发现有的同学只用一个梯形就推导出了梯形的面积计算公式,你们想看看吗?
(一)借助拼摆,自主探究
预设一:
7. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?
梯形的面积=小三角形的面积+大三角形的面积
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
(一)借助拼摆,自主探究
预设二:
7. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?
=(上底+下底)×高÷2
梯形的面积=平行四边形的面积+三角形的面积
=上底×高+(下底-上底)×高÷2
(一)借助拼摆,自主探究
预设四:
7. 暴露资源,组织研讨:谁愿意说说你们是怎么想的?
平行四边形的面积= 底 × 高
梯形的面积 (上底+下底)÷2 高
梯形的面积=(上底+下底)×高÷2
(一)借助拼摆,自主探究
8. 总结概括,提升认识:通过同学们刚才的汇报,我们发现只要是运用相应的方法把梯形分割或割补成学过的图形,然后找到相应的新旧图形的联系,充分论证了梯形的面积=(上底+下底)×高÷2。
9. 如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积计算公式是: S=(a+b)h÷2
s=(a+b)h÷2
=(36+120)×135÷2
= 156×135÷2
答:这个梯形的面积是10530平方米。
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
一辆汽车侧面的两块玻璃的形状是梯形(如下图),它们的面积分别是多少?
S =(a+b)h÷2
=(40+71)×40÷2
=111×40÷2
S =(a+b)h÷2
=(45+65)×40÷2
=110×40÷2
1.两个完全一样的梯形可以拼成一个平行四边形,这个平行四边形的底等于梯形的( )与( )的和,高等于梯形的( ),每个梯形的面积等于拼成的平行 四边形面积的( )。
提高练习
2.一个梯形的上底是12米,下底是8米,高是4米,面积是( )平方米。
上底
下 底
高
一半
4 0
判断
1、梯形的面积公式用字母表示是:S=(a+b)h
梯形的面积公式用字母表示是:S=(a+b)h÷2
2、两个梯形的高相等,它们的面积就相等。
3、两个面积相等梯形可以拼成一个平行四边形。
两个完全一样的梯形可以拼成一个平行四边形。
4、两个面积相等的梯形一定能拼成一个平行四边形。 ( )
5、平行四边形的面积一定比梯形的面积大。( )
6、一个平行四边形可以分成两个梯形 。 ( )
寻找合适的条件,求出图中阴影梯形的面积
S=(a+b)h÷2
=(18+12) × 9÷2
=30 × 9÷2
=135(平方厘米)
7-4=3(厘米)
S=(a+b)h÷2
=(7+3) × 5÷2
=10 × 5÷2
=25(平方厘米)
8-2-1=5(厘米)
S=(a+b)h÷2
= (5+8) ×4÷2
=13 × 4÷2
=26(平方厘米)
1、用篱笆围成一个梯形养鸡场(如图),其中一边利用房屋墙壁。已知篱笆长80m,求养鸡场的占地面积。
提示:靠墙的一边不用围篱笆。有两个直角,20m相当于梯形的高,那么46m减去20m,剩下的是什么?
(46-20)×20÷2
=26×20÷2
=520÷2
一条新挖的水渠,横截面是梯形(如图),渠口宽2.8m,渠底宽1.4m,渠深1.2m。它的横向横截面的面积是多少平方米?
(2.8+1.4)×1.2÷2
=4.2×1.2÷2
=5.04÷2
=2.52 ( 平方米 )
答:它的横截面积是2.52平方米。
已知一个梯形的上底、下底和面积,求高是多少?
10m
20m
解:设高是x米。
(25+10)x÷2=140
35x÷2=140
35x÷2×2=140×2
35x=280
35x÷35=280÷35
x=8
答:高是8米。
还有没有其它的方法?
140×2÷(25+10)
=140×2÷35
=280÷35
=8(米)
答:高是8米。
练习二十一
1.一条新挖的水渠,横截面是梯形。渠口宽2.8m,渠底宽1.4m,渠深1.2m。横截面的面积是多少平方米?
S=(a+b)h÷2
=(36+120)×135÷2
=156×135÷2
答:横截面的面积是10530平方米。
练习二十一
2. 计算下面每个梯形的面积。
S =(a+b)h÷2
=(3+4)×5÷2
=12×5÷2
S =(a+b)h÷2
=(8.2+5.9)×4.8÷2
=14.1×4.8÷2
S =(a+b)h÷2
=(12+15)×20÷2
=27×20÷2
练习二十一
3.自己想办法求出这两个梯形的面积。
练习二十一
4.科技小组制作飞机模型,机翼的平面图是由两个完全相同的梯形组成的,机翼的面积是多少?
S=(a+b)h÷2
=(48+100)×250÷2
=148×250÷2
练习二十一
5.寻找合适的条件,求出下图中涂色梯形的面积。(单位:cm)
S =(a+b)h÷2
=(12+18)×6÷2
=30×6÷2
S =(a+b)h÷2
=(5-2.3+5)×3.4÷2
=7.7×3.4÷2
S =(a+b)h÷2
=(7.2-2.2-1.6 +7.2)×4.8÷2
=10.6×4.8÷2
练习二十一
6. 靠墙边围成一个花坛,围花坛的篱笆长46m,求这个花坛的面积。
这个梯形的上底和下底和:
46-20 =26(m)
S=(a+b)h÷2
=26×20÷2
练习二十一
解:设下底是x厘米
(4.5+x)×3÷2=15
(4.5+x)×3=15×2
(4.5+x)×3=30
(4.5+x)=30÷3
4.5+x=10
x=10 -4.5
x=5.5
答:下底是5.5厘米。
练习二十一
8.我们经常见到圆木、钢管等堆成像下图的形状。通常采用下面的方法求总根数:
(2+6)×5÷2
=8×5÷2
=20(根)
答:圆木的总根数是20根。
练习二十一
9. 在周围找一个梯形,量出它的底和高,再算出它的面积。
练习二十一
S=(a+b)h÷2
=(160+180)×50÷2
=340×50÷2
8500÷10=850(棵)
答:这个果园共有果树850棵。
练习二十一
11.在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少?有几种求法?
剩下的是一个三角形
(3.5-2)×1.8÷2
=1.5×1.8÷2
答:剩下的面积是1.35平方厘米。
=1.35(平方厘米)
