笑迎中考温馨提示2012年中考数学防错十八诀
文档属性
| 名称 | 笑迎中考温馨提示2012年中考数学防错十八诀 |

|
|
| 格式 | zip | ||
| 文件大小 | 79.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-16 00:00:00 | ||
图片预览










文档简介
(共47张PPT)
温馨提示 笑迎中考
—2012年中考数学防错“十八诀”
教学效果显著的老师
姓甚名谁?
一个姓(李)理,叫理得清
一个姓(丁)盯,叫盯得紧
课上理得清
课后盯得紧
“冷面杀手”;
“温柔一刀”
纠错教学能使中考复习的效益最大化
1 边边角,别胡搅
两边及其一边的对角对应相等的两个三角形不一定全等,所以“边边角”是不能作为三角形全等的识别方法,谨防误用.
边边角,不正确
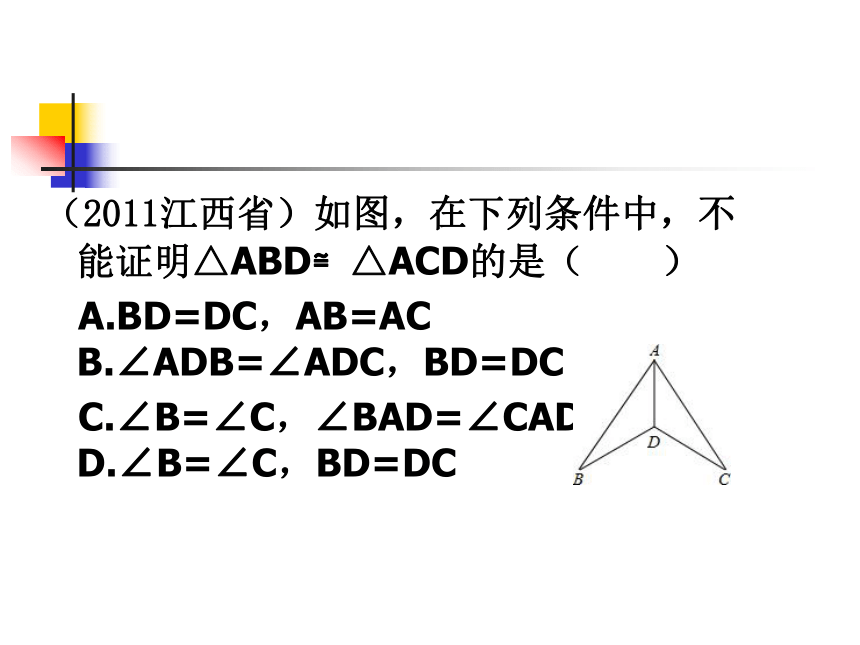
(2011江西省)如图,在下列条件中,不能证明△ABD≌△ACD的是( )
A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
2 相似符号没有写,
注意对应防多解
在相似三角形中由于对应关系的多样性,当题目涉及到的两个相似三角形没有给出相似符号“∽”时,千万要注意对应,此时一般要分类讨论.
(2011临沂,26,13分)如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上的第一象限内
的动点,过点P作PM⊥x轴,垂足
为M,是否存在点P,使得以P、
M、A为顶点的三角形△BOC相似?
若存在,求出点P的坐标;若不存在,
请说明理由.
3 等腰要求边和角,
分类讨论不可少
不少学生在涉及到求等腰三角形的边长和内角大小的问题时,当题目中没有明确边和内角时,常常把腰和底边、顶角和底角相互混淆,出现以偏概全,从而导致漏解.
(2011山东烟台)等腰三角形的周长为14,其一边长为4,那么,它的底边为 .
(2010 楚雄)已知等腰三角形的一个内角为 ,则另外两个内角的度数是( ).
4 直径与半径, 混淆太差劲
在同圆或等圆中,直径是半径的2倍,半径是直径是一半,此概念人人清楚,但在解题时,不少同学粗心大意,不是将直径看成半径,就是将半径当成直径,应避免此类低级错误.
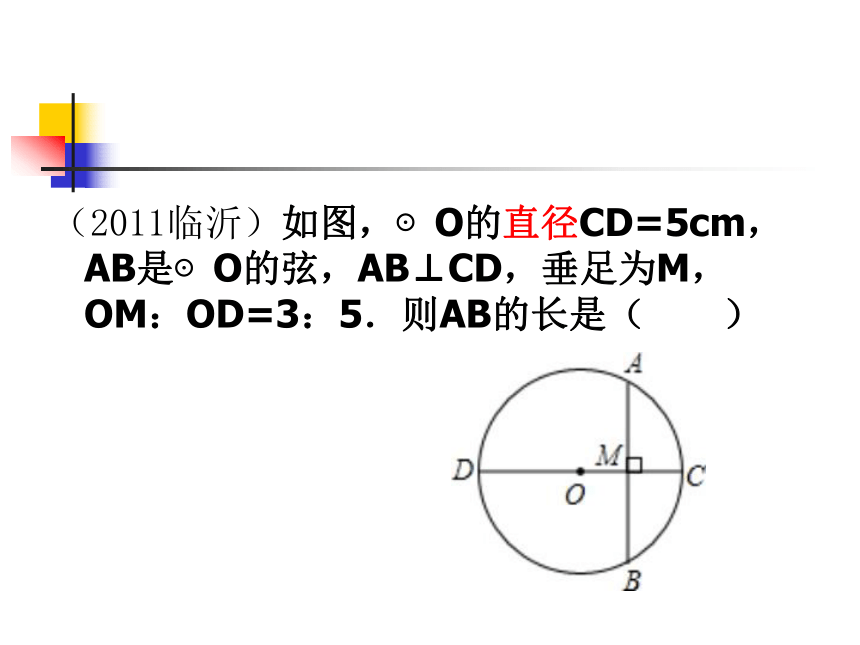
(2011临沂)如图,⊙O的直径CD=5cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )
5 两圆相切,内切外切
圆与圆的位置关系包括种:外离、外切、相交、内切和包含.因此,两圆相切就应包含内切和外切两种位置关系,切勿遗漏.
(2011乌鲁木齐)如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒的速度从A点出发,沿AC向点C移动.同时,动点Q以1米/秒的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.
(1)略;(2)略;
(3)以P为圆心,PA为半径
的圆与以Q为圆心,QC为半
径的圆相切时,求出t的值.
6 侧面积,表面积,
易相混,要注意
圆柱的表面积=圆柱侧面积+两底面积,圆锥的表面积=圆锥侧面积+底面积,不可混淆.
(2011山东泰安)一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是( )
A.5π B. 4π
C.3π D.2π
(2011湖北黄冈)一个几何体的三视图如下:其中主视图都是腰长为4、底边为2的等腰三角形,则这个几何体的侧面展开图的面积为( )
A. B.
C. D.
7 去分母, 防漏乘
在解方程或解不等式的过程中,如需去分母,千万不能漏乘不含分母的项.
(2010 南宁)将分式方程
去分母,整理后得( ).
A. B.
C. D.
8 乱约分,要失根
一元二次方程根的判别式表明:当△≥0时方程有两个实数根,当△>0时方程有两个不相等的实数根,当△=0时有两个相等的实数根.也就是说一元二次方程如果有实数根,那么应该有两个(相等或不相等).但在实际解题过程中,如果方程两边同除以含未知数的代数式时,容易破坏方程的同解性,从而丢失一个根.
(2011泰州)一元二次方程x2=2x的根是
A.x=2 B.x=0
C.x1=0, x2=2 D.x1=0, x2=-2
(2010 呼和浩特)方程
的根是 .
9 乘除是负数,转向要记住
不等式性质与等式性质最显著的区别是:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
(2011盐城)
解不等式组
并把解集在数轴上表示出来.
10 方程关于爱克斯(x)
一次二次要深思
课本上的一元二次方程的定义是:只含有一个未知数,并且未知数的最高次数是的整式方程叫做一元二次方程.任何一个关于的一元二次方程,经过整理,都能化成ax2+bx+c=0(a≠0)的形式.由此可见,二次项系数a≠0是应满足的条件,解题时不能忽略.
( 2011重庆江津)已知关于x的一元二次方程(a-1)x2-2x+1=0有两个不相等的实数根,则a的取值范围是( )
A.a<2 B.a>2
C.a<2且a≠1 D.a<-2·
11 上零下不零,
分式值为零
分式的值为0的条件是:分子为0且分母不为0.其中,分母不为0这一条件学生常常疏忽.
(2011天津)若分式
的值为0,则x的值等于_____ .
12 分式求值有文章
取值范围记心上
近年来各地中考中频繁出现一类开放性分式化简、求值试题,这类题型一般要求将给定的分式先化简,然后选取一个你认为合适的数作为相关字母的值代入求值.命题者往往喜爱在自选“合适的数”上大做文章,设置陷阱.解这类题目时,学生往往容易疏忽“分式的分母不能为零”这一隐含条件,所选数值有时恰好使原分式的分母为零或化简过程中的分式分母为零,从而导致错误.
(2010 深圳)先化简分式
然后在0,1,2,3中选一个你认为合适的 值,代入求值.
13 等不等,整不整
对于一些需要列不等式解决的数学问题,列不等式所用的符号,是用“≥”(或“≤”),还是用“>”(或“<”),究竟带不带“=”,一定要搞清楚,不能粗心大意.另外,不少实际问题,还需要求整数解,切勿将其遗漏.
(2011四川眉山)关于x的不等式3x﹣a≤0,只有两个正整数解,则a的取值范围是 .
14 实际问题画图象,
取值范围记心上
在一些实际问题中,要求根据题意画出函数的图象,此时特别要注意函数中自变量的取值范围,画出的图象必须在自变量的取值范围内.
15 矩形面积值,k的绝对值
涉及到反比例函数的面积问题,有一个非常实用的基本结论:如图,从反比例函数 (k≠0)的图象上任意一点A(x,y)分别作AB⊥X轴于B、y轴于B, 由此可见,矩形ABOB的面积是一个不变量,恒为 ,这个基本结论揭示了反比例函数比例系数的本质(几何意义).运用此结论时,应该要特别注意k的符号的确定,否则极易出错.
(2010 甘肃)如图,矩形 ABOC 的面积为3,
反比例函数 的图象过点A,则k=___
图4
16 函数关于爱克斯(x)
一次二次要深思
形如y= ax2+bx+c(a≠0) (a、b、c为常数,且a≠0 )的函数叫做二次函数,这里的a≠0 ,必不可少.如果a=0 , b≠0 ,则函数y= ax2+bx+c为一次函数.
(2011南京)已知函数y=mx2﹣6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
(2010 盐城)已知:函数 y= ax2+bx+1 的图象与轴只有一个公共点.
(1)求这个函数关系式;
(2)略;
(3)略.
17 放回不放回,眼光要敏锐
在概率教学中,“放回还是不放回”一直是学生的易错点和模糊点,一般来说,由于操作方式不同,放回与不放回所得的结果大都是不同的.尤其要指出的是,有些题目中的“一次性摸两个(张)”,其实就是属于不放回问题.
(2010 南京)某厂为新型号电视机上市举办促销活动,顾客每购买一台该型号电视机可获得一次抽奖机会,该厂拟按10%设大奖,其余90%为小奖. 厂家设计的抽奖方案是:在一个不透明的盒子中,放入10个黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球的顾客获得大奖,摸到白球的顾客获得小奖.(1)厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2个黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖.该抽奖文案符合厂家的设奖要求吗?请说明理由;
(2)略
18 单位要统一,列式要注意
用方程(组)、不等式(组)或函数解决问题,列式时同类量的单位必须一致,要注意常用的长度单位(厘米、米、千米)、时间单位(秒、分、时)、重量单位(克、千克、吨)、货币单位(元、万元、亿元)的换算.
(2010 绍兴)某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为275万元?
温馨提示 笑迎中考
—2012年中考数学防错“十八诀”
教学效果显著的老师
姓甚名谁?
一个姓(李)理,叫理得清
一个姓(丁)盯,叫盯得紧
课上理得清
课后盯得紧
“冷面杀手”;
“温柔一刀”
纠错教学能使中考复习的效益最大化
1 边边角,别胡搅
两边及其一边的对角对应相等的两个三角形不一定全等,所以“边边角”是不能作为三角形全等的识别方法,谨防误用.
边边角,不正确
(2011江西省)如图,在下列条件中,不能证明△ABD≌△ACD的是( )
A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
2 相似符号没有写,
注意对应防多解
在相似三角形中由于对应关系的多样性,当题目涉及到的两个相似三角形没有给出相似符号“∽”时,千万要注意对应,此时一般要分类讨论.
(2011临沂,26,13分)如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上的第一象限内
的动点,过点P作PM⊥x轴,垂足
为M,是否存在点P,使得以P、
M、A为顶点的三角形△BOC相似?
若存在,求出点P的坐标;若不存在,
请说明理由.
3 等腰要求边和角,
分类讨论不可少
不少学生在涉及到求等腰三角形的边长和内角大小的问题时,当题目中没有明确边和内角时,常常把腰和底边、顶角和底角相互混淆,出现以偏概全,从而导致漏解.
(2011山东烟台)等腰三角形的周长为14,其一边长为4,那么,它的底边为 .
(2010 楚雄)已知等腰三角形的一个内角为 ,则另外两个内角的度数是( ).
4 直径与半径, 混淆太差劲
在同圆或等圆中,直径是半径的2倍,半径是直径是一半,此概念人人清楚,但在解题时,不少同学粗心大意,不是将直径看成半径,就是将半径当成直径,应避免此类低级错误.
(2011临沂)如图,⊙O的直径CD=5cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )
5 两圆相切,内切外切
圆与圆的位置关系包括种:外离、外切、相交、内切和包含.因此,两圆相切就应包含内切和外切两种位置关系,切勿遗漏.
(2011乌鲁木齐)如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒的速度从A点出发,沿AC向点C移动.同时,动点Q以1米/秒的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.
(1)略;(2)略;
(3)以P为圆心,PA为半径
的圆与以Q为圆心,QC为半
径的圆相切时,求出t的值.
6 侧面积,表面积,
易相混,要注意
圆柱的表面积=圆柱侧面积+两底面积,圆锥的表面积=圆锥侧面积+底面积,不可混淆.
(2011山东泰安)一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是( )
A.5π B. 4π
C.3π D.2π
(2011湖北黄冈)一个几何体的三视图如下:其中主视图都是腰长为4、底边为2的等腰三角形,则这个几何体的侧面展开图的面积为( )
A. B.
C. D.
7 去分母, 防漏乘
在解方程或解不等式的过程中,如需去分母,千万不能漏乘不含分母的项.
(2010 南宁)将分式方程
去分母,整理后得( ).
A. B.
C. D.
8 乱约分,要失根
一元二次方程根的判别式表明:当△≥0时方程有两个实数根,当△>0时方程有两个不相等的实数根,当△=0时有两个相等的实数根.也就是说一元二次方程如果有实数根,那么应该有两个(相等或不相等).但在实际解题过程中,如果方程两边同除以含未知数的代数式时,容易破坏方程的同解性,从而丢失一个根.
(2011泰州)一元二次方程x2=2x的根是
A.x=2 B.x=0
C.x1=0, x2=2 D.x1=0, x2=-2
(2010 呼和浩特)方程
的根是 .
9 乘除是负数,转向要记住
不等式性质与等式性质最显著的区别是:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
(2011盐城)
解不等式组
并把解集在数轴上表示出来.
10 方程关于爱克斯(x)
一次二次要深思
课本上的一元二次方程的定义是:只含有一个未知数,并且未知数的最高次数是的整式方程叫做一元二次方程.任何一个关于的一元二次方程,经过整理,都能化成ax2+bx+c=0(a≠0)的形式.由此可见,二次项系数a≠0是应满足的条件,解题时不能忽略.
( 2011重庆江津)已知关于x的一元二次方程(a-1)x2-2x+1=0有两个不相等的实数根,则a的取值范围是( )
A.a<2 B.a>2
C.a<2且a≠1 D.a<-2·
11 上零下不零,
分式值为零
分式的值为0的条件是:分子为0且分母不为0.其中,分母不为0这一条件学生常常疏忽.
(2011天津)若分式
的值为0,则x的值等于_____ .
12 分式求值有文章
取值范围记心上
近年来各地中考中频繁出现一类开放性分式化简、求值试题,这类题型一般要求将给定的分式先化简,然后选取一个你认为合适的数作为相关字母的值代入求值.命题者往往喜爱在自选“合适的数”上大做文章,设置陷阱.解这类题目时,学生往往容易疏忽“分式的分母不能为零”这一隐含条件,所选数值有时恰好使原分式的分母为零或化简过程中的分式分母为零,从而导致错误.
(2010 深圳)先化简分式
然后在0,1,2,3中选一个你认为合适的 值,代入求值.
13 等不等,整不整
对于一些需要列不等式解决的数学问题,列不等式所用的符号,是用“≥”(或“≤”),还是用“>”(或“<”),究竟带不带“=”,一定要搞清楚,不能粗心大意.另外,不少实际问题,还需要求整数解,切勿将其遗漏.
(2011四川眉山)关于x的不等式3x﹣a≤0,只有两个正整数解,则a的取值范围是 .
14 实际问题画图象,
取值范围记心上
在一些实际问题中,要求根据题意画出函数的图象,此时特别要注意函数中自变量的取值范围,画出的图象必须在自变量的取值范围内.
15 矩形面积值,k的绝对值
涉及到反比例函数的面积问题,有一个非常实用的基本结论:如图,从反比例函数 (k≠0)的图象上任意一点A(x,y)分别作AB⊥X轴于B、y轴于B, 由此可见,矩形ABOB的面积是一个不变量,恒为 ,这个基本结论揭示了反比例函数比例系数的本质(几何意义).运用此结论时,应该要特别注意k的符号的确定,否则极易出错.
(2010 甘肃)如图,矩形 ABOC 的面积为3,
反比例函数 的图象过点A,则k=___
图4
16 函数关于爱克斯(x)
一次二次要深思
形如y= ax2+bx+c(a≠0) (a、b、c为常数,且a≠0 )的函数叫做二次函数,这里的a≠0 ,必不可少.如果a=0 , b≠0 ,则函数y= ax2+bx+c为一次函数.
(2011南京)已知函数y=mx2﹣6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
(2010 盐城)已知:函数 y= ax2+bx+1 的图象与轴只有一个公共点.
(1)求这个函数关系式;
(2)略;
(3)略.
17 放回不放回,眼光要敏锐
在概率教学中,“放回还是不放回”一直是学生的易错点和模糊点,一般来说,由于操作方式不同,放回与不放回所得的结果大都是不同的.尤其要指出的是,有些题目中的“一次性摸两个(张)”,其实就是属于不放回问题.
(2010 南京)某厂为新型号电视机上市举办促销活动,顾客每购买一台该型号电视机可获得一次抽奖机会,该厂拟按10%设大奖,其余90%为小奖. 厂家设计的抽奖方案是:在一个不透明的盒子中,放入10个黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球的顾客获得大奖,摸到白球的顾客获得小奖.(1)厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2个黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖.该抽奖文案符合厂家的设奖要求吗?请说明理由;
(2)略
18 单位要统一,列式要注意
用方程(组)、不等式(组)或函数解决问题,列式时同类量的单位必须一致,要注意常用的长度单位(厘米、米、千米)、时间单位(秒、分、时)、重量单位(克、千克、吨)、货币单位(元、万元、亿元)的换算.
(2010 绍兴)某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为275万元?
同课章节目录
