北师大版九年级数学上册新思维同步提高训练(Word版含解答):1.1菱形的性质与判定
文档属性
| 名称 | 北师大版九年级数学上册新思维同步提高训练(Word版含解答):1.1菱形的性质与判定 |
|
|
| 格式 | docx | ||
| 文件大小 | 385.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 00:00:00 | ||
图片预览




文档简介
北师大版九年级数学上册新思维同步训练提高:1.1菱形的性质与判定
一、选择题
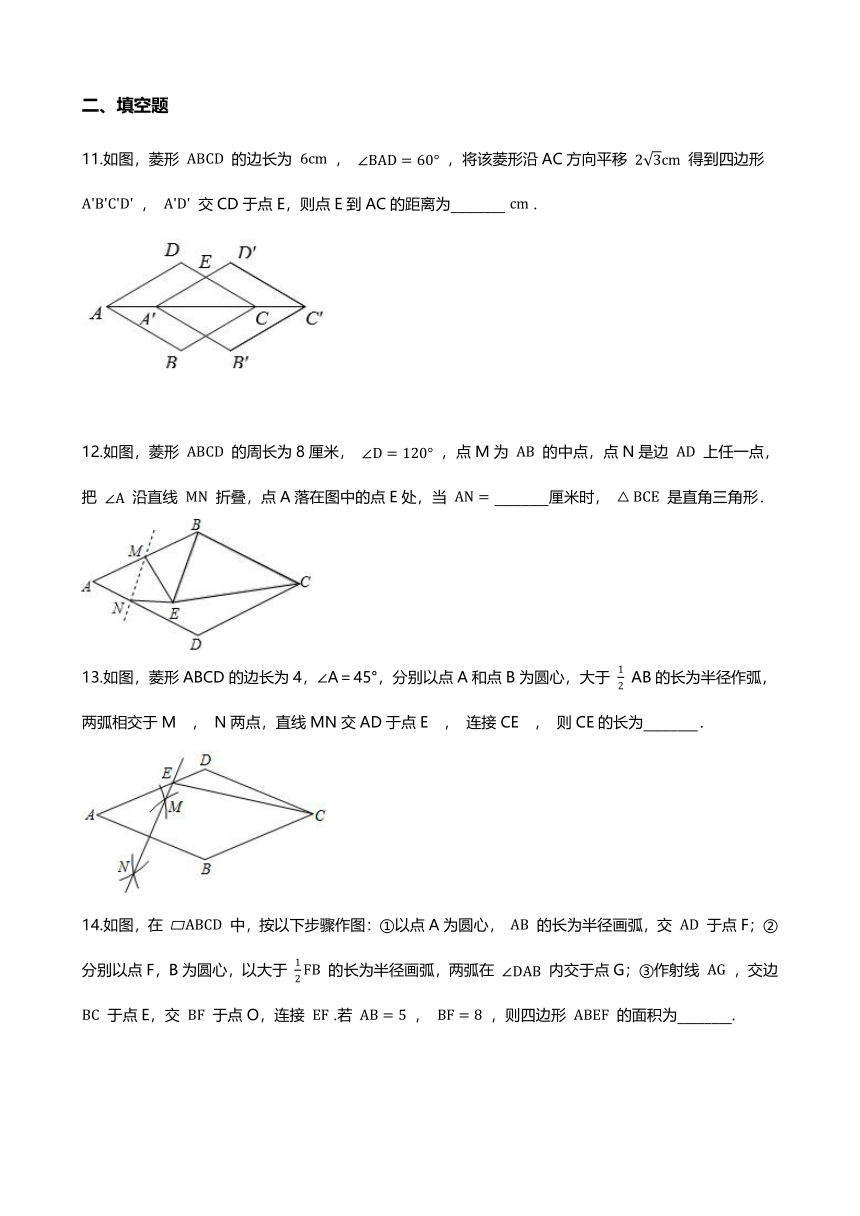
1.如图,菱形ABCD中,AC交BD于点O , DE⊥BC于点E , 连接OE , 若∠ABC=140°,则∠OED=( )
A.?20°???????????????????????B.?30°???????????????????????C.?40°???????????????????D.?50°
2.如图,菱形ABCD的对角线AC、BD相交于点O , 过点D作DH⊥AB于点H , 连接OH , 若OA=6,S菱形ABCD=48,则OH的长为(??? )
A.?4????????????????????????B.?8?????????????????????????????C.?13?????????????????????D.?6
3.如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则EF的长为(??? )??
?
A.?74??????????????B.?95??????????????????C.?1910??????????????????????D.?763
4.如图,菱形ABCD中, ∠B=60° ,点P从点B出发,沿折线 BC-CD 方向移动,移动到点D停止.在 △ABP 形状的变化过程中,依次出现的特殊三角形是(?? )
A.?直角三角形→等边三角形→等腰三角形→直角三角形
B.?直角三角形→等腰三角形→直角三角形→等边三角形
C.?直角三角形→等边三角形→直角三角形→等腰三角形
D.?等腰三角形→等边三角形→直角三角形→等腰三角形
5.数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是(?? )
A.?用3个相同的菱形放置,最多能得到6个菱形?????B.?用4个相同的菱形放置,最多能得到15个菱形
C.?用5个相同的菱形放置,最多能得到27个菱形????D.?用6个相同的菱形放置,最多能得到41个菱形
6.如图,已知点P是菱形 ABCD 的对角线 AC 延长线上一点,过点P分别作 AD 、 DC 延长线的垂线,垂足分别为点E、F.若 ∠ABC=120° , AB=2 ,则 PE-PF 的值为(?? )
A.?32??????????????????????B.?3?????????????????????????????C.?2????????????????????????????D.?52
7.如图,菱形 ABCD 对角线 AC , BD 交于点 O , ∠ACB=15° ,过点 C 作 CE⊥AD 交 AD 的延长线于点 E .若菱形 ABCD 的面积为4,则菱形的边长为(?? )
A.?22??????????????????????B.?2????????????????????????C.?42??????????????????????D.?4
8.如图,菱形ABCD中,∠A=60°,边AB=8,E为边DA的中点,P为边CD上的一点,连接PE、PB,当PE=EB时,线段PE的长为(? )
A.?4??????????????????????B.?8????????????????????C.?4 6???????????????????????D.?4 3
9.如图,在菱形 ABCD 中, M,N 分别是边 CD,BC 的中点,P是对角线 BD 上一动点,已知菱形边长为5,对角线 AC 长为6,则 △PMN 周长的最小值是( )
A.?11???????????????????????????????B.?10??????????????????????????C.?9???????????????????????????D.?8
10.如图,菱形 ABCD 的对角线的长分别为2和5,P是对角线 AC 上任一点(点P不与点A,C重合),且 PE//BC 交 AB 于E, PF//CD 交 AD 于F,则阴影部分的面积是(??? )
A.?10???????????????????????????????B.?7.5???????????????????C.?5??????????????????????D.?2.5
二、填空题
11.如图,菱形 ABCD 的边长为 6cm , ∠BAD=60° ,将该菱形沿AC方向平移 23cm 得到四边形 A'B'C'D' , A'D' 交CD于点E,则点E到AC的距离为________ cm .
?
12.如图,菱形 ABCD 的周长为8厘米, ∠D=120° ,点M为 AB 的中点,点N是边 AD 上任一点,把 ∠A 沿直线 MN 折叠,点A落在图中的点E处,当 AN= ________厘米时, △BCE 是直角三角形.
13.如图,菱形ABCD的边长为4,∠A=45°,分别以点A和点B为圆心,大于 12 AB的长为半径作弧,两弧相交于M , N两点,直线MN交AD于点E , 连接CE , 则CE的长为________.
14.如图,在 ?ABCD 中,按以下步骤作图:①以点A为圆心, AB 的长为半径画弧,交 AD 于点F;②分别以点F,B为圆心,以大于 12FB 的长为半径画弧,两弧在 ∠DAB 内交于点G;③作射线 AG ,交边 BC 于点E,交 BF 于点O,连接 EF .若 AB=5 , BF=8 ,则四边形 ABEF 的面积为________.
15.如图, △ ABC是边长为1的等边三角形,取BC边中点E , 作ED∥AB , EF∥AC , 得到四边形EDAF , 它的周长记作C1;取BE中点E1 , 作E1D1∥FB , E1F1∥EF , 得到四边形E1D1FF1 , 它的周长记作C2 . 照此规律作下去,则C2021=________.
16.如图,已知菱形ABCD的边长为6,点M是对角线AC上的一动点,目∠ABC=120°,则MA+MB+MD的最小值是________.
三、解答题
17.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA、DC的延长线分别交于点E、F.
(1)求证:AE=CF;
(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.
18.已知:如图,在□ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
19.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.
(1)求证:AE=BF;
(2)若点E恰好是AD的中点,AB=2,求BD的值.
20.如图,已知菱形ABCD中,分别以C、D为圆心,大于 12 CD的长为半径作弧,两弧分别相交于M、N两点,直线MN交CD于点F , 交对角线AC于点E , 连接BE、DE .
(1)求证:BE=CE;
(2)若∠ABC=72°,求∠ABE的度数.
21.点E、F分别在菱形 ABCD 的边 BC 、 CD 上, BE=DF ,作 FG//AE ,交 AC 的延长线于点G,连接 AF 、 EG .
(1)如图1,求证:四边形 AEGF 是菱形;
(2)如图2,当 AF 平分 ∠CAD 时,在不添加辅助线及字母的情况下,请直接写出图中所有的等腰三角形(不包括腰长等于 AB 的等腰三角形)
22.如图, RtΔABC 中, ∠C=90° , D 是 AB 上一点, DE⊥AC 于点 E , F 是 AD 的中点, FG⊥BC 于点 G ,与 DE 交于点 H ,若 FG=AF , AG 平分 ∠CAB ,连结 GE , GD .
(1)求证: ΔECG≌ΔGHD ;
(2)求证: AD=AC+EC .
(3)若 ∠B=30° ,判定四边形 AEGF 是否为菱形,并说明理由.
23.?ABCD ,过点D作 ED⊥AD 交 AB 的延长线于点E, BE=AB .
(1)如图1,求证:四边形 BDCE 是菱形;
(2)P为线段 BC 上一点,点M,N在直线 AE 上,且 PM=PB , ∠DPN=∠BPM .
①当 ∠A=60° 时,如图2,求证: CD=PB+BN .
②当 ∠A=45° 时,如图3,线段 CD , PB , BN 的数量关系如何?(请直接写出猜想的结论)
24.在平面直角坐标系 xOy 中,对于点A和线段 MN ,如果点A , O , M , N按逆时针方向排列构成菱形 AOMN ,且 ∠AOM=α ,则称线段 MN 是点A的“ α- 相关线段”.例如,图1中线段 MN 是点A的“ 30° -相关线段”.
(1)已知点A的坐标是 (0,2) .
①在图2中画出点A的“ 30° -相关线段” MN ,并直接写出点M和点N的坐标;
②若点A的“ α -相关线段”经过点 (3,1) ,求 α 的值;
(2)若存在 α,β(α≠β) 使得点P的“ α -相关线段”和“ β -相关线段”都经过点 (0,4) ,记 PO=t ,直接写出t的取值范围.
25.如图l,四边形 ABCD 为菱形, AB=m , ∠DAB=60° , DE⊥AB 于点 E , F 为 BC 上任意一点,连接 DF , BD , H 为 DF 上任意一点.
(1)若 DF⊥BC ,求 DF 的长(用 m 表示).
(2)如图2,作 FG//DE 交 AC 于点 G , H 为 DF 的中点,连接 HG , HB , BG .猜想线段 HG 与 HB 存在的数量关系,并证明你猜想的结论.
(3)在点 F 的运动过程中,当 HB+HC+HD 的值最小时,请直接写出 HF 的长(用 m 表示).
答案
一、选择题
1.解:∵四边形ABCD是菱形,
∴O为BD中点,∠DBE= 12 ∠ABC=70°.
∵DE⊥BC ,
∴在Rt△BDE中,OE=BE=OD ,
∴∠OEB=∠OBE=70°.
∴∠OED=90°﹣70°=20°.
故答案为:A .
2.解:∵四边形ABCD是菱形,
∴OA=OC=6,OB=OD , AC⊥BD ,
∴AC=12,
∵DH⊥AB ,
∴∠BHD=90°,
∴ OH=12BD ,
∵菱形ABCD的面积 =12×AC×BD=12×12×BD=48 ,
∴BD=8,
∴ OH=12BD=4 ;
故答案为:A.
3.解:连接BE , BD , 如图,?
∵四边形ABCD为菱形,∠A=60°,?
∴△BDC为等边三角形, ∠C=∠A=60°,
∴∠CBE=90°-60°=30°.
∵E点为CD的中点,?
∴CE=DE=1,BE⊥CD.?
在Rt△BCE中,
BC=2CE=2,
BE= 22-12=3 .?
∵AB∥CD,?
∴BE⊥AB.
∵菱形纸片翻折,使点A落在CD的中点E处,
∴EF=AF.
设EF=AF=x,则BF=2-x,?
在Rt△BEF中,
(2-x)2+(3)2=x2 ,
解得 x=7x .
故答案为:A.?
4.解:连接AC,BD,如图所示.
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠D=∠B.
∵∠B=60°,
∴∠D=∠B=60°.
∴△ABC和△ADC都是等边三角形.
点P在移动过程中,依次共有四个特殊位置:
(1)当点P移动到BC边的中点时,记作 P1 .
∵△ABC是等边三角形, P1 是 BC的中点,
∴ AP1⊥BC .
∴ ∠AP1B=90° .
∴△ABP1是直角三角形.
(2)当点P与点C重合时,记作 P2 .
此时,△ABP2是等边三角形;
(3)当点P移动到CD边的中点时,记为 P3 .
∵△ABC和△ADC都是等边三角形,
∴ ∠P3AB=30°+60°=90° .
∴△ABP3是直角三角形.
(4)当点P与点D重合时,记作 P4 .
∵ AB=AP4 ,
∴△ABP4是等腰三角形.
综上,△ABP形状的变化过程中,依次出现的特殊三角形是:
直角三角形→等边三角形→直角三角形→等腰三角形.
故答案为:C
5.解:用2个相同的菱形放置,最多能得到3个菱形,
用3个相同的菱形放置,最多能得到8个菱形,
?
用4个相同的菱形放置,最多能得到15个菱形,
用5个相同的菱形放置,最多能得到22个菱形,
用6个相同的菱形放置,最多能得到29个菱形,
故答案为:B.
6.解:∵四边形ABCD是菱形且∠ABC=120°,AB=2,
∴AB=BC=CD=DA=2,∠BAD=60°,AC⊥BD,
∴∠CAE=30?,
∵AC⊥BD,∠CAE=30°,AD=2,
∴AC= 222-12=23 ,
∴AP= 23 +PC,
在直角△AEP中,
∵∠PAE=30°,AP= 23 +PC,
∴PE= 12 AP= 3 + 12 PC,
在直角△PFC中,
∵∠PCF=30°,
∴PF= 12 PC,
∴ PE-PF = 3 + 12 PC- 12 PC= 3 ,
故答案为:B.
7.解:∵四边形ABCD是菱形,
∴AD=CD,AD∥BC,
∴∠EDC=∠BCD=2∠ACB=30°,
∵CE⊥AD,
∴∠CED=90°,
∴CE= 12 DC= 12 AD,
∴菱形ABCD的面积=AD?CE=AD? 12 AD= 12 AD2=4,
∴AD= 22 (负值舍去),
即菱形的边长为 22 ,
故答案为:A.
8.解:连接BD,
∵四边形ABCD是菱形,
∴AB=AD=8,且∠A=60°,
∴△ABD是等边三角形,且点E是AD的中点,
∴BE⊥AD,
∴AE=4,∠ABE=30°,
∴ BE=43 ,
∵PE=BE
∴ PE=43 ,
故答案为:D.
9.解:如图,作点M关于BD的对称点 M' ,连接 M'N 交BD于点 P' .
根据对称的性质和菱形的性质可知点 M' 为AD的中点.
又∵点N为BC中点,
∴ M'N 经过点O , 即点O与点 P' 重合.
∵ P'M'=P'M ,
∴根据两点直线线段最短可知,当 P' 点为P点时, PM+PN 最小为 M'N 长,即此时 △PMN 的周长最小.
∵AC=6,
∴ AO=12AC=3 .
在 Rt△AOD 中, DO=AD2-AO2=52-32=4 ,
∴ BD=2DO=8 .
∵点M , N分别为DC , BC的中点,
∴ MN=12BD=4 .
∵点 M' ,N分别为AD , BC的中点,
∴ AM'=BN ,
又∵ AM'//BN ,
∴四边形 ABNM' 为平行四边形.
∴ M'N=AB=5 ,
∴ M'N+MN=5+4=9 ,即 △PMN 的周长最小值为9.
故答案为:C.
10.解:设AP与EF相交于O点.
∵四边形ABCD为菱形,
∴BC//AD,AB//CD.
∵PE//BC,PF//CD,
∴PE//AF,PF//AE.
∴四边形AEFP是平行四边形.
∴S△POF=S△AOE .
即阴影部分的面积等于△ABC的面积.
∵△ABC的面积等于菱形ABCD的面积的一半,
菱形ABCD的面积= 12 AC?BD=5,
∴图中阴影部分的面积为 12 ×5=2.5.
故答案为:D.
二、填空题
11.∵∠BAD=60°,
?
∴连接对角线AC,BD,则AC⊥BD,且AC平分∠BAD,???
∴在Rt△ADO中, DO=12AD=12×6=3
利用勾股定理得 AO=AD2-DO2=62-32=33
又∵AC=2AO,
∴AC= 63 ,
由题可知 AA' = 23 ,
∴A’C= AC-AA'=63-23=43 ;
由平移可知 ∠D'A'C =∠DAC=30°,而∠DAC=∠DCA,???
∴ ∠D'A'C =∠DCA,即 ∠EA'C = ∠ECA' =30°,
∴ △EA'C 是等腰三角形;
过点E作EF⊥AC,垂足为F,如图所示:
则由等腰三角形三线合一可得:A’F=FC= 12A'C=23 ,
在Rt△ECF中, EF=12EC ,设EF=x,则EC=2x,
由勾股定理得: CF2+EF2=EC2
x2+(23)2=(2x)2 ,解得x=2,
故填:2.
12.解:∵菱形 ABCD 的周长为8厘米,
∴AB=BC=CD=AD=2厘米,
∵点M为 AB 的中点,
∴ AM=BM=1 厘米.
由翻折可知 EM=AM=BM ,
∴ ∠MBE=∠MEB .
①当 ∠EBC=90° 时, ∠D=120° ,
∴ ∠ABC=120° , ∠A=60° ,
∴ ∠MBE=∠MEB=30° ,
∴ ∠BME=120° ,
∴ ∠AMN=∠EMN=30° ,
∴ ∠MNA=90° , AN=12AM=12 厘米;
②当 ∠BEC=90° 时,点E在以M为圆心,AM为半径的圆上,也在以BC为直径的圆上,根据菱形ABCD的特点,可知点E落在菱形对角线 AC 上,
∵点M为 AB 的中点, MN 为折痕,此时 BD⊥AC 于点E ,
∴点N为 AD 的中点, AN=12AD=1 厘米.
当 AN=12 或1厘米时, △BCE 是直角三角形.
13.解:
连接BE,AB与MN交点记为F,
根据作图方式,可知MN为边AB的垂直平分线,
所以MN⊥AB,AF=BF,
因为四边形ABCD为菱形,∠A=45°,
所以∠ABE=45°,∠ABC=135°
所以∠EBC=90°,△EBC为直角三角形,
因为菱形ABCD的边长为4,
所以AF=BF=2,BE=22+22=22
所以在Rt△EBC中,CE=BE2+BC2=222+42=26
14.解:由作图可知,AG平分∠BAF,AB=AF,
∴AG垂直平分BF,∠FAG=∠BAE,
∴EF=EB,
∵AD∥BE,
∴∠FAE=∠AEB,
∴∠BAE =∠AEB,
∴AB=BE,
∴AB=BE=EF=AF,
∴四边形ABEF是菱形,
∴BO=FO=4,
∴ OA=AB2-OB2=52-42=3 ,
AE=6,
菱形 ABEF 的面积为 12AE?BF=12×6×8=24 ;
故答案为:24.
15.解:∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵E是BC的中点,ED∥AB ,
∴DE是△ABC的中位线,
∴DE= 12 AB= 12 ,AD= 12 AC= 12 ,
∵EF∥AC ,
∴四边形EDAF是菱形,
∴C1=4× 12 ,…,
∴ Cn =4× 12n ,
∴C2021=4× 122021 = 122019 ,
故答案为: 122019 .
16.如图,作DE⊥AB于E点,连接BD,
∵菱形ABCD中,∠ABC=120°,
∴∠DAB=60°,则△ABD为等边三角形,
∴∠MAE=30°,
∴AM=2ME,
∵MD=MB,
∴MA+MB+MD=2ME+2MD=2DE,
根据垂线段最短,此时DE最短,即MA+MB+MD最小,
∵菱形的边长为6,
∴AB=6,AE=3,
∴ DE=AD2-AE2=33 ,
∴ 2DE=63 ,
∴MA+MB+MD最小值为 63 ,
故答案为: 63 .
三、解答题
17. (1)证明:∵四边形 ABCD 是平行四边形
∴OA=OC,BE∥DF
∴∠E=∠F
在△AOE和△COF中 {∠E=∠F∠AOE=∠COFOA=OC
∴ △AOE≌△COF (AAS)
∴AE=CF
(2)解:当EF⊥BD时,四边形BFDE是菱形,理由如下:
如图:连结BF,DE
∵四边形 ABCD 是平行四边形
∴OB=OD
∵ △AOE≌△COF
∴ OE=OF ?????????????????????????
∴四边形 BFDE 是平行四边形
∵EF⊥BD,
∴四边形 BFDE 是菱形
18.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC
∴∠EDO=∠FBO
又∵O为对角线BD的中点,
∴BO=DO,在△DOE和△BOF中
{∠EDO=∠FBODO=BO∠EOD=∠FOB ,
∴△DOE≌△BOF(ASA)
(2)解:当∠DOE=90°时,四边形BFDE为菱形,
理由:∵△DOE≌△BOF,
∴OE=OF,
又∵OB=OD
∴四边形EBFD是平行四边形,
∵∠EOD=90°,
∴EF⊥BD,
∴四边形BFDE为菱形.
19. (1)证明:四边形ABCD是菱形
∴AB=BC,AD∥BC
∴∠A=∠CBF
∵BE⊥AD、CF⊥AB
∴∠AEB=∠BFC=90°
∴△AEB≌△BFC(AAS)
∴AE=BF
(2)解:∵E是AD中点,且BE⊥AD
∴直线BE为AD的垂直平分线
∴BD=AB=2
20. (1)证明:∵四边形ABCD是菱形,
∴CB=CD,∠ACB=∠ACD,
在△ECB和△ECD中,
{CE=CE∠ECB=∠ECDCB=CD ,
∴△ECB≌△ECD(SAS),
∴BE=DE,
由作图可知,MN垂直平分线段CD,
∴EC=ED,
∴BE=CE.
(2)解:∵BA=BC,∠ABC=72°,
∴∠BAC=∠BCA= 12 (180°﹣72°)=54°,
∵EB=EC,
∴∠EBC=∠ECB=54°,
∴∠ABE=∠ABC﹣∠EBC=18°.
21.(1)证明:∵ABCD为菱形,
∴AB=AD,∠B=∠D,∠BAC=∠DAC,
∵BE=DF,
∴△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∴∠EAG=∠FAG,
∵FG//AE,
∴∠EAG=∠FGA,
∴∠FAG=∠FGA,
∴FG=AF=AE,
∵FG//AE,
∴四边形 AEGF是平行四边形,
又AE=AF,
∴四边形 AEGF 是菱形
(2)解:由(1)及菱形的性质可得△AEG、△AFG是等腰三角形,
∴∠FAC=∠FGA,
由已知∠DAC=2∠FAC,
∴∠DAC=2∠FGA,
又AD=DC,
∴∠DAC=∠DCA,
∵∠DCA=∠FGA+∠CFG,
∴2∠FGA=∠FGA+∠CFG,
∴∠FGA=∠CFG,
∴△CFG是等腰三角形,
同理可得△CEG也是等腰三角形,
∴符合要求的等腰三角形为△AEG、△AFG、△CEG、△CFG.
22. (1)证明:∵AF=FG,
∴∠FAG=∠FGA,
∵AG平分∠CAB,
∴∠CAG=∠FAG,
∴∠CAG=∠FGA,
∴AC∥FG,
∵DE⊥AC,
∴FG⊥DE,
∵FG⊥BC,
∴DE∥BC,
∴AC⊥BC,
∴∠C=∠DHG=90°,∠CGE=∠GED,
∵F是AD的中点,FG∥AE,
∴H是ED的中点,
∴FG是线段ED的垂直平分线,
∴GE=GD,∠GDE=∠GED,
∴∠CGE=∠GDE,
∴△ECG≌△GHD;
(2)证明:过点G作GP⊥AB于P,
∴GC=GP,而AG=AG,
∴△CAG≌△PAG,
∴AC=AP,
由(1)可得EG=DG,
∴Rt△ECG≌Rt△DPG,
∴EC=PD,
∴AD=AP+PD=AC+EC;
(3)解:四边形AEGF是菱形,
证明:∵∠B=30°,
∴∠ADE=30°,
∴AE= 12 AD,
∴AE=AF=FG,
由(1)得AE∥FG,
∴四边形AEGF是平行四边形,
∴四边形AEGF是菱形.
23. (1)证明:∵BE=AB,且ED⊥AD,
即BD为Rt△ADE斜边的的中线,
∴BD=BE=AB= 12AE ,
∵四边形ABCD是平行四边形,
∴AB=CD, AB∥CD,
∴BE =CD,BE∥CD,
∴四边形BDCE是平行四边形,
又∵BD=BE,
∴四边形BDCE是菱形;
(2)解:①∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠PBM=∠A=60°,
∵PM=PB,
∴△PBM是等边三角形,
∴PM=PB=BM,
∵∠DPN=∠BPM,
∴∠DPN+∠BPN =∠BPM+∠BPN,即∠DPB =∠NPM,
∵四边形BDCE是菱形,
∴∠DBP =∠NMP=60°,
在△DBP和△NMP中,
{∠DPB=∠NPMPB=PM∠DBP=∠NMP ,
∴△DBP ? △NMP(ASA),
∴MN=BD=BE,BM+BN=BM+ME,
∴BN=ME,
∴CD=BE=BM+ME=PB+BN;
②CD+ BN= 2 PB
解:(2)②∵∠A=45°,且ED⊥AD ,
?∴△ADE是等腰直角三角形,
∴∠DEA=45°,
同(1)法可证明四边形BDCE是正方形,
同①可得∠DPN=∠BPM ,
∴∠DPN-∠BPN =∠BPM-∠BPN , 即∠DPB =∠NPM ,
∵PM=PB ,
∴∠MBP =∠NMP=45°,
∴△MBP是等腰直角三角形,
即∠MBP =∠NMP=45°=∠PBD ,
在△DBP和△NMP中,
{∠DPB=∠NPMPB=PM∠DBP=∠NMP ,
∴△DBP ? △NMP(ASA),
∴MN=BD=BE , BM+BN=BM+ME ,
∴BN=ME ,
∵△MBP是等腰直角三角形,
∴BM= 2 PB=MN+BN=BD+BN=CD+ BN;
即CD+ BN= 2 PB .
24.(1)解:①如图, MN 即为所求.
过点M作BM⊥x轴于点B,
∵四边形AOMN为菱形,
∴AO∥MN,AO=MO=MN,
∵点A在y轴上,
∴AO⊥x轴,
∴MN⊥x轴,即N、M、B三点共线,
∵∠AOM=30°,
∴∠MOB=90°-30°=60°,
在RT△MOB中,BO= 12 MO=1,MB= 32MO=3 ,
∴点M的坐标是 (1,3) ,点N的坐标是 (1,3+2) .
②解:∵点A的“ α -相关线段” MN 经过点 (3,1) ,
∴点M必在直线 x=3 上.
记直线 x=3 与x轴交于点 H(3,0) ,
∵ OM=OA=2,OH=3 ,
∴ MH=OM2-OH2=1 , ∠MOH=30° .
分两种情况:
a)如图,当点M在x轴上方时,点M恰为 (3,1) ,符合题意,此时 ∠AOM=60°,α=60° ;
b)如图,当点M在x轴下方时,点M为 (3,-1) ,由 MN=2 知点N为 (3,1) ,也符合题意,此时 ∠AOM=120°,α=120° .
综上, α 的值为 60° 或 120° .
(2)当0当2 2 当t>4时,只有一种情况使P的“α-相关线段”或“β-相关线段”过(0,4),此时(0,4)在线段OM上,
∴不符合题意
综上所述, 2225. (1)解:∵ ABCD 为菱形, ∠DAB=60°
∴ △DAB , △DBC 为等边三角形
∴由三线合一知, DE=AD2+(AB2)2=m2+(m2)2=32m
∵ DE⊥AB , DF⊥BC
∴ ∠DBE=∠DFB=90°
又 DB=DB
∴ △DEB≌△DFB
∴ DE=DF=32m
(2)解: HB=3HG
证明:延长 GH 交 DE 于点 M ,连接 MB
由题意知 ∠1=∠ACB=30° , ∠2=∠3=60°
∵ FG//DE
∴ ∠3=∠AGF=∠GCB+∠GFC=60° , ∠HFG=∠HDM
∴ ∠GFC=∠GCF=30°
∴ GF=GC
∵ H 为 DC 的中点
∴ HF=HD
∵ ∠GHF=∠MHD
∴ △HGF≌△HMD
∴ GF=MD , HM=HG
∴ MD=CG
在 △DMB 和 △CGB 中
{∠MDB=∠GCB=30°MD=GCDB=CB
∴ △DMB ≌ △CGB
∴ BM=BG , ∠MBD=∠GBC
∴ ∠MBG=∠DBC=60°
∴ △MBG 为等边三角形
∴ BH⊥MG
∴ HB=3HG
(3)解: HF=36m
作 △BHC 关于点 B 顺时旋转 60° ,得到 △BH'C' ,
∴ △BHH' 为等边三角形
∴ HB+HC+HD=HD+HH'+H'C'
当点 D , H , H' , C' 四点共线时, HD+HH'+H'C' 值最小
连接 CC'
此时有 BC=BC' , ∠CBC'=60°
∴ △BCC' 为等边三角形
∵ DB=DC , C'B=C'C
∴ DC' 为 BC 的垂直平分线
∴ BF 垂直平分 HH'
∴ ∠HBF=∠FBH'=30°
∴ HF= false
一、选择题
1.如图,菱形ABCD中,AC交BD于点O , DE⊥BC于点E , 连接OE , 若∠ABC=140°,则∠OED=( )
A.?20°???????????????????????B.?30°???????????????????????C.?40°???????????????????D.?50°
2.如图,菱形ABCD的对角线AC、BD相交于点O , 过点D作DH⊥AB于点H , 连接OH , 若OA=6,S菱形ABCD=48,则OH的长为(??? )
A.?4????????????????????????B.?8?????????????????????????????C.?13?????????????????????D.?6
3.如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则EF的长为(??? )??
?
A.?74??????????????B.?95??????????????????C.?1910??????????????????????D.?763
4.如图,菱形ABCD中, ∠B=60° ,点P从点B出发,沿折线 BC-CD 方向移动,移动到点D停止.在 △ABP 形状的变化过程中,依次出现的特殊三角形是(?? )
A.?直角三角形→等边三角形→等腰三角形→直角三角形
B.?直角三角形→等腰三角形→直角三角形→等边三角形
C.?直角三角形→等边三角形→直角三角形→等腰三角形
D.?等腰三角形→等边三角形→直角三角形→等腰三角形
5.数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是(?? )
A.?用3个相同的菱形放置,最多能得到6个菱形?????B.?用4个相同的菱形放置,最多能得到15个菱形
C.?用5个相同的菱形放置,最多能得到27个菱形????D.?用6个相同的菱形放置,最多能得到41个菱形
6.如图,已知点P是菱形 ABCD 的对角线 AC 延长线上一点,过点P分别作 AD 、 DC 延长线的垂线,垂足分别为点E、F.若 ∠ABC=120° , AB=2 ,则 PE-PF 的值为(?? )
A.?32??????????????????????B.?3?????????????????????????????C.?2????????????????????????????D.?52
7.如图,菱形 ABCD 对角线 AC , BD 交于点 O , ∠ACB=15° ,过点 C 作 CE⊥AD 交 AD 的延长线于点 E .若菱形 ABCD 的面积为4,则菱形的边长为(?? )
A.?22??????????????????????B.?2????????????????????????C.?42??????????????????????D.?4
8.如图,菱形ABCD中,∠A=60°,边AB=8,E为边DA的中点,P为边CD上的一点,连接PE、PB,当PE=EB时,线段PE的长为(? )
A.?4??????????????????????B.?8????????????????????C.?4 6???????????????????????D.?4 3
9.如图,在菱形 ABCD 中, M,N 分别是边 CD,BC 的中点,P是对角线 BD 上一动点,已知菱形边长为5,对角线 AC 长为6,则 △PMN 周长的最小值是( )
A.?11???????????????????????????????B.?10??????????????????????????C.?9???????????????????????????D.?8
10.如图,菱形 ABCD 的对角线的长分别为2和5,P是对角线 AC 上任一点(点P不与点A,C重合),且 PE//BC 交 AB 于E, PF//CD 交 AD 于F,则阴影部分的面积是(??? )
A.?10???????????????????????????????B.?7.5???????????????????C.?5??????????????????????D.?2.5
二、填空题
11.如图,菱形 ABCD 的边长为 6cm , ∠BAD=60° ,将该菱形沿AC方向平移 23cm 得到四边形 A'B'C'D' , A'D' 交CD于点E,则点E到AC的距离为________ cm .
?
12.如图,菱形 ABCD 的周长为8厘米, ∠D=120° ,点M为 AB 的中点,点N是边 AD 上任一点,把 ∠A 沿直线 MN 折叠,点A落在图中的点E处,当 AN= ________厘米时, △BCE 是直角三角形.
13.如图,菱形ABCD的边长为4,∠A=45°,分别以点A和点B为圆心,大于 12 AB的长为半径作弧,两弧相交于M , N两点,直线MN交AD于点E , 连接CE , 则CE的长为________.
14.如图,在 ?ABCD 中,按以下步骤作图:①以点A为圆心, AB 的长为半径画弧,交 AD 于点F;②分别以点F,B为圆心,以大于 12FB 的长为半径画弧,两弧在 ∠DAB 内交于点G;③作射线 AG ,交边 BC 于点E,交 BF 于点O,连接 EF .若 AB=5 , BF=8 ,则四边形 ABEF 的面积为________.
15.如图, △ ABC是边长为1的等边三角形,取BC边中点E , 作ED∥AB , EF∥AC , 得到四边形EDAF , 它的周长记作C1;取BE中点E1 , 作E1D1∥FB , E1F1∥EF , 得到四边形E1D1FF1 , 它的周长记作C2 . 照此规律作下去,则C2021=________.
16.如图,已知菱形ABCD的边长为6,点M是对角线AC上的一动点,目∠ABC=120°,则MA+MB+MD的最小值是________.
三、解答题
17.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA、DC的延长线分别交于点E、F.
(1)求证:AE=CF;
(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.
18.已知:如图,在□ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
19.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.
(1)求证:AE=BF;
(2)若点E恰好是AD的中点,AB=2,求BD的值.
20.如图,已知菱形ABCD中,分别以C、D为圆心,大于 12 CD的长为半径作弧,两弧分别相交于M、N两点,直线MN交CD于点F , 交对角线AC于点E , 连接BE、DE .
(1)求证:BE=CE;
(2)若∠ABC=72°,求∠ABE的度数.
21.点E、F分别在菱形 ABCD 的边 BC 、 CD 上, BE=DF ,作 FG//AE ,交 AC 的延长线于点G,连接 AF 、 EG .
(1)如图1,求证:四边形 AEGF 是菱形;
(2)如图2,当 AF 平分 ∠CAD 时,在不添加辅助线及字母的情况下,请直接写出图中所有的等腰三角形(不包括腰长等于 AB 的等腰三角形)
22.如图, RtΔABC 中, ∠C=90° , D 是 AB 上一点, DE⊥AC 于点 E , F 是 AD 的中点, FG⊥BC 于点 G ,与 DE 交于点 H ,若 FG=AF , AG 平分 ∠CAB ,连结 GE , GD .
(1)求证: ΔECG≌ΔGHD ;
(2)求证: AD=AC+EC .
(3)若 ∠B=30° ,判定四边形 AEGF 是否为菱形,并说明理由.
23.?ABCD ,过点D作 ED⊥AD 交 AB 的延长线于点E, BE=AB .
(1)如图1,求证:四边形 BDCE 是菱形;
(2)P为线段 BC 上一点,点M,N在直线 AE 上,且 PM=PB , ∠DPN=∠BPM .
①当 ∠A=60° 时,如图2,求证: CD=PB+BN .
②当 ∠A=45° 时,如图3,线段 CD , PB , BN 的数量关系如何?(请直接写出猜想的结论)
24.在平面直角坐标系 xOy 中,对于点A和线段 MN ,如果点A , O , M , N按逆时针方向排列构成菱形 AOMN ,且 ∠AOM=α ,则称线段 MN 是点A的“ α- 相关线段”.例如,图1中线段 MN 是点A的“ 30° -相关线段”.
(1)已知点A的坐标是 (0,2) .
①在图2中画出点A的“ 30° -相关线段” MN ,并直接写出点M和点N的坐标;
②若点A的“ α -相关线段”经过点 (3,1) ,求 α 的值;
(2)若存在 α,β(α≠β) 使得点P的“ α -相关线段”和“ β -相关线段”都经过点 (0,4) ,记 PO=t ,直接写出t的取值范围.
25.如图l,四边形 ABCD 为菱形, AB=m , ∠DAB=60° , DE⊥AB 于点 E , F 为 BC 上任意一点,连接 DF , BD , H 为 DF 上任意一点.
(1)若 DF⊥BC ,求 DF 的长(用 m 表示).
(2)如图2,作 FG//DE 交 AC 于点 G , H 为 DF 的中点,连接 HG , HB , BG .猜想线段 HG 与 HB 存在的数量关系,并证明你猜想的结论.
(3)在点 F 的运动过程中,当 HB+HC+HD 的值最小时,请直接写出 HF 的长(用 m 表示).
答案
一、选择题
1.解:∵四边形ABCD是菱形,
∴O为BD中点,∠DBE= 12 ∠ABC=70°.
∵DE⊥BC ,
∴在Rt△BDE中,OE=BE=OD ,
∴∠OEB=∠OBE=70°.
∴∠OED=90°﹣70°=20°.
故答案为:A .
2.解:∵四边形ABCD是菱形,
∴OA=OC=6,OB=OD , AC⊥BD ,
∴AC=12,
∵DH⊥AB ,
∴∠BHD=90°,
∴ OH=12BD ,
∵菱形ABCD的面积 =12×AC×BD=12×12×BD=48 ,
∴BD=8,
∴ OH=12BD=4 ;
故答案为:A.
3.解:连接BE , BD , 如图,?
∵四边形ABCD为菱形,∠A=60°,?
∴△BDC为等边三角形, ∠C=∠A=60°,
∴∠CBE=90°-60°=30°.
∵E点为CD的中点,?
∴CE=DE=1,BE⊥CD.?
在Rt△BCE中,
BC=2CE=2,
BE= 22-12=3 .?
∵AB∥CD,?
∴BE⊥AB.
∵菱形纸片翻折,使点A落在CD的中点E处,
∴EF=AF.
设EF=AF=x,则BF=2-x,?
在Rt△BEF中,
(2-x)2+(3)2=x2 ,
解得 x=7x .
故答案为:A.?
4.解:连接AC,BD,如图所示.
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠D=∠B.
∵∠B=60°,
∴∠D=∠B=60°.
∴△ABC和△ADC都是等边三角形.
点P在移动过程中,依次共有四个特殊位置:
(1)当点P移动到BC边的中点时,记作 P1 .
∵△ABC是等边三角形, P1 是 BC的中点,
∴ AP1⊥BC .
∴ ∠AP1B=90° .
∴△ABP1是直角三角形.
(2)当点P与点C重合时,记作 P2 .
此时,△ABP2是等边三角形;
(3)当点P移动到CD边的中点时,记为 P3 .
∵△ABC和△ADC都是等边三角形,
∴ ∠P3AB=30°+60°=90° .
∴△ABP3是直角三角形.
(4)当点P与点D重合时,记作 P4 .
∵ AB=AP4 ,
∴△ABP4是等腰三角形.
综上,△ABP形状的变化过程中,依次出现的特殊三角形是:
直角三角形→等边三角形→直角三角形→等腰三角形.
故答案为:C
5.解:用2个相同的菱形放置,最多能得到3个菱形,
用3个相同的菱形放置,最多能得到8个菱形,
?
用4个相同的菱形放置,最多能得到15个菱形,
用5个相同的菱形放置,最多能得到22个菱形,
用6个相同的菱形放置,最多能得到29个菱形,
故答案为:B.
6.解:∵四边形ABCD是菱形且∠ABC=120°,AB=2,
∴AB=BC=CD=DA=2,∠BAD=60°,AC⊥BD,
∴∠CAE=30?,
∵AC⊥BD,∠CAE=30°,AD=2,
∴AC= 222-12=23 ,
∴AP= 23 +PC,
在直角△AEP中,
∵∠PAE=30°,AP= 23 +PC,
∴PE= 12 AP= 3 + 12 PC,
在直角△PFC中,
∵∠PCF=30°,
∴PF= 12 PC,
∴ PE-PF = 3 + 12 PC- 12 PC= 3 ,
故答案为:B.
7.解:∵四边形ABCD是菱形,
∴AD=CD,AD∥BC,
∴∠EDC=∠BCD=2∠ACB=30°,
∵CE⊥AD,
∴∠CED=90°,
∴CE= 12 DC= 12 AD,
∴菱形ABCD的面积=AD?CE=AD? 12 AD= 12 AD2=4,
∴AD= 22 (负值舍去),
即菱形的边长为 22 ,
故答案为:A.
8.解:连接BD,
∵四边形ABCD是菱形,
∴AB=AD=8,且∠A=60°,
∴△ABD是等边三角形,且点E是AD的中点,
∴BE⊥AD,
∴AE=4,∠ABE=30°,
∴ BE=43 ,
∵PE=BE
∴ PE=43 ,
故答案为:D.
9.解:如图,作点M关于BD的对称点 M' ,连接 M'N 交BD于点 P' .
根据对称的性质和菱形的性质可知点 M' 为AD的中点.
又∵点N为BC中点,
∴ M'N 经过点O , 即点O与点 P' 重合.
∵ P'M'=P'M ,
∴根据两点直线线段最短可知,当 P' 点为P点时, PM+PN 最小为 M'N 长,即此时 △PMN 的周长最小.
∵AC=6,
∴ AO=12AC=3 .
在 Rt△AOD 中, DO=AD2-AO2=52-32=4 ,
∴ BD=2DO=8 .
∵点M , N分别为DC , BC的中点,
∴ MN=12BD=4 .
∵点 M' ,N分别为AD , BC的中点,
∴ AM'=BN ,
又∵ AM'//BN ,
∴四边形 ABNM' 为平行四边形.
∴ M'N=AB=5 ,
∴ M'N+MN=5+4=9 ,即 △PMN 的周长最小值为9.
故答案为:C.
10.解:设AP与EF相交于O点.
∵四边形ABCD为菱形,
∴BC//AD,AB//CD.
∵PE//BC,PF//CD,
∴PE//AF,PF//AE.
∴四边形AEFP是平行四边形.
∴S△POF=S△AOE .
即阴影部分的面积等于△ABC的面积.
∵△ABC的面积等于菱形ABCD的面积的一半,
菱形ABCD的面积= 12 AC?BD=5,
∴图中阴影部分的面积为 12 ×5=2.5.
故答案为:D.
二、填空题
11.∵∠BAD=60°,
?
∴连接对角线AC,BD,则AC⊥BD,且AC平分∠BAD,???
∴在Rt△ADO中, DO=12AD=12×6=3
利用勾股定理得 AO=AD2-DO2=62-32=33
又∵AC=2AO,
∴AC= 63 ,
由题可知 AA' = 23 ,
∴A’C= AC-AA'=63-23=43 ;
由平移可知 ∠D'A'C =∠DAC=30°,而∠DAC=∠DCA,???
∴ ∠D'A'C =∠DCA,即 ∠EA'C = ∠ECA' =30°,
∴ △EA'C 是等腰三角形;
过点E作EF⊥AC,垂足为F,如图所示:
则由等腰三角形三线合一可得:A’F=FC= 12A'C=23 ,
在Rt△ECF中, EF=12EC ,设EF=x,则EC=2x,
由勾股定理得: CF2+EF2=EC2
x2+(23)2=(2x)2 ,解得x=2,
故填:2.
12.解:∵菱形 ABCD 的周长为8厘米,
∴AB=BC=CD=AD=2厘米,
∵点M为 AB 的中点,
∴ AM=BM=1 厘米.
由翻折可知 EM=AM=BM ,
∴ ∠MBE=∠MEB .
①当 ∠EBC=90° 时, ∠D=120° ,
∴ ∠ABC=120° , ∠A=60° ,
∴ ∠MBE=∠MEB=30° ,
∴ ∠BME=120° ,
∴ ∠AMN=∠EMN=30° ,
∴ ∠MNA=90° , AN=12AM=12 厘米;
②当 ∠BEC=90° 时,点E在以M为圆心,AM为半径的圆上,也在以BC为直径的圆上,根据菱形ABCD的特点,可知点E落在菱形对角线 AC 上,
∵点M为 AB 的中点, MN 为折痕,此时 BD⊥AC 于点E ,
∴点N为 AD 的中点, AN=12AD=1 厘米.
当 AN=12 或1厘米时, △BCE 是直角三角形.
13.解:
连接BE,AB与MN交点记为F,
根据作图方式,可知MN为边AB的垂直平分线,
所以MN⊥AB,AF=BF,
因为四边形ABCD为菱形,∠A=45°,
所以∠ABE=45°,∠ABC=135°
所以∠EBC=90°,△EBC为直角三角形,
因为菱形ABCD的边长为4,
所以AF=BF=2,BE=22+22=22
所以在Rt△EBC中,CE=BE2+BC2=222+42=26
14.解:由作图可知,AG平分∠BAF,AB=AF,
∴AG垂直平分BF,∠FAG=∠BAE,
∴EF=EB,
∵AD∥BE,
∴∠FAE=∠AEB,
∴∠BAE =∠AEB,
∴AB=BE,
∴AB=BE=EF=AF,
∴四边形ABEF是菱形,
∴BO=FO=4,
∴ OA=AB2-OB2=52-42=3 ,
AE=6,
菱形 ABEF 的面积为 12AE?BF=12×6×8=24 ;
故答案为:24.
15.解:∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵E是BC的中点,ED∥AB ,
∴DE是△ABC的中位线,
∴DE= 12 AB= 12 ,AD= 12 AC= 12 ,
∵EF∥AC ,
∴四边形EDAF是菱形,
∴C1=4× 12 ,…,
∴ Cn =4× 12n ,
∴C2021=4× 122021 = 122019 ,
故答案为: 122019 .
16.如图,作DE⊥AB于E点,连接BD,
∵菱形ABCD中,∠ABC=120°,
∴∠DAB=60°,则△ABD为等边三角形,
∴∠MAE=30°,
∴AM=2ME,
∵MD=MB,
∴MA+MB+MD=2ME+2MD=2DE,
根据垂线段最短,此时DE最短,即MA+MB+MD最小,
∵菱形的边长为6,
∴AB=6,AE=3,
∴ DE=AD2-AE2=33 ,
∴ 2DE=63 ,
∴MA+MB+MD最小值为 63 ,
故答案为: 63 .
三、解答题
17. (1)证明:∵四边形 ABCD 是平行四边形
∴OA=OC,BE∥DF
∴∠E=∠F
在△AOE和△COF中 {∠E=∠F∠AOE=∠COFOA=OC
∴ △AOE≌△COF (AAS)
∴AE=CF
(2)解:当EF⊥BD时,四边形BFDE是菱形,理由如下:
如图:连结BF,DE
∵四边形 ABCD 是平行四边形
∴OB=OD
∵ △AOE≌△COF
∴ OE=OF ?????????????????????????
∴四边形 BFDE 是平行四边形
∵EF⊥BD,
∴四边形 BFDE 是菱形
18.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC
∴∠EDO=∠FBO
又∵O为对角线BD的中点,
∴BO=DO,在△DOE和△BOF中
{∠EDO=∠FBODO=BO∠EOD=∠FOB ,
∴△DOE≌△BOF(ASA)
(2)解:当∠DOE=90°时,四边形BFDE为菱形,
理由:∵△DOE≌△BOF,
∴OE=OF,
又∵OB=OD
∴四边形EBFD是平行四边形,
∵∠EOD=90°,
∴EF⊥BD,
∴四边形BFDE为菱形.
19. (1)证明:四边形ABCD是菱形
∴AB=BC,AD∥BC
∴∠A=∠CBF
∵BE⊥AD、CF⊥AB
∴∠AEB=∠BFC=90°
∴△AEB≌△BFC(AAS)
∴AE=BF
(2)解:∵E是AD中点,且BE⊥AD
∴直线BE为AD的垂直平分线
∴BD=AB=2
20. (1)证明:∵四边形ABCD是菱形,
∴CB=CD,∠ACB=∠ACD,
在△ECB和△ECD中,
{CE=CE∠ECB=∠ECDCB=CD ,
∴△ECB≌△ECD(SAS),
∴BE=DE,
由作图可知,MN垂直平分线段CD,
∴EC=ED,
∴BE=CE.
(2)解:∵BA=BC,∠ABC=72°,
∴∠BAC=∠BCA= 12 (180°﹣72°)=54°,
∵EB=EC,
∴∠EBC=∠ECB=54°,
∴∠ABE=∠ABC﹣∠EBC=18°.
21.(1)证明:∵ABCD为菱形,
∴AB=AD,∠B=∠D,∠BAC=∠DAC,
∵BE=DF,
∴△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∴∠EAG=∠FAG,
∵FG//AE,
∴∠EAG=∠FGA,
∴∠FAG=∠FGA,
∴FG=AF=AE,
∵FG//AE,
∴四边形 AEGF是平行四边形,
又AE=AF,
∴四边形 AEGF 是菱形
(2)解:由(1)及菱形的性质可得△AEG、△AFG是等腰三角形,
∴∠FAC=∠FGA,
由已知∠DAC=2∠FAC,
∴∠DAC=2∠FGA,
又AD=DC,
∴∠DAC=∠DCA,
∵∠DCA=∠FGA+∠CFG,
∴2∠FGA=∠FGA+∠CFG,
∴∠FGA=∠CFG,
∴△CFG是等腰三角形,
同理可得△CEG也是等腰三角形,
∴符合要求的等腰三角形为△AEG、△AFG、△CEG、△CFG.
22. (1)证明:∵AF=FG,
∴∠FAG=∠FGA,
∵AG平分∠CAB,
∴∠CAG=∠FAG,
∴∠CAG=∠FGA,
∴AC∥FG,
∵DE⊥AC,
∴FG⊥DE,
∵FG⊥BC,
∴DE∥BC,
∴AC⊥BC,
∴∠C=∠DHG=90°,∠CGE=∠GED,
∵F是AD的中点,FG∥AE,
∴H是ED的中点,
∴FG是线段ED的垂直平分线,
∴GE=GD,∠GDE=∠GED,
∴∠CGE=∠GDE,
∴△ECG≌△GHD;
(2)证明:过点G作GP⊥AB于P,
∴GC=GP,而AG=AG,
∴△CAG≌△PAG,
∴AC=AP,
由(1)可得EG=DG,
∴Rt△ECG≌Rt△DPG,
∴EC=PD,
∴AD=AP+PD=AC+EC;
(3)解:四边形AEGF是菱形,
证明:∵∠B=30°,
∴∠ADE=30°,
∴AE= 12 AD,
∴AE=AF=FG,
由(1)得AE∥FG,
∴四边形AEGF是平行四边形,
∴四边形AEGF是菱形.
23. (1)证明:∵BE=AB,且ED⊥AD,
即BD为Rt△ADE斜边的的中线,
∴BD=BE=AB= 12AE ,
∵四边形ABCD是平行四边形,
∴AB=CD, AB∥CD,
∴BE =CD,BE∥CD,
∴四边形BDCE是平行四边形,
又∵BD=BE,
∴四边形BDCE是菱形;
(2)解:①∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠PBM=∠A=60°,
∵PM=PB,
∴△PBM是等边三角形,
∴PM=PB=BM,
∵∠DPN=∠BPM,
∴∠DPN+∠BPN =∠BPM+∠BPN,即∠DPB =∠NPM,
∵四边形BDCE是菱形,
∴∠DBP =∠NMP=60°,
在△DBP和△NMP中,
{∠DPB=∠NPMPB=PM∠DBP=∠NMP ,
∴△DBP ? △NMP(ASA),
∴MN=BD=BE,BM+BN=BM+ME,
∴BN=ME,
∴CD=BE=BM+ME=PB+BN;
②CD+ BN= 2 PB
解:(2)②∵∠A=45°,且ED⊥AD ,
?∴△ADE是等腰直角三角形,
∴∠DEA=45°,
同(1)法可证明四边形BDCE是正方形,
同①可得∠DPN=∠BPM ,
∴∠DPN-∠BPN =∠BPM-∠BPN , 即∠DPB =∠NPM ,
∵PM=PB ,
∴∠MBP =∠NMP=45°,
∴△MBP是等腰直角三角形,
即∠MBP =∠NMP=45°=∠PBD ,
在△DBP和△NMP中,
{∠DPB=∠NPMPB=PM∠DBP=∠NMP ,
∴△DBP ? △NMP(ASA),
∴MN=BD=BE , BM+BN=BM+ME ,
∴BN=ME ,
∵△MBP是等腰直角三角形,
∴BM= 2 PB=MN+BN=BD+BN=CD+ BN;
即CD+ BN= 2 PB .
24.(1)解:①如图, MN 即为所求.
过点M作BM⊥x轴于点B,
∵四边形AOMN为菱形,
∴AO∥MN,AO=MO=MN,
∵点A在y轴上,
∴AO⊥x轴,
∴MN⊥x轴,即N、M、B三点共线,
∵∠AOM=30°,
∴∠MOB=90°-30°=60°,
在RT△MOB中,BO= 12 MO=1,MB= 32MO=3 ,
∴点M的坐标是 (1,3) ,点N的坐标是 (1,3+2) .
②解:∵点A的“ α -相关线段” MN 经过点 (3,1) ,
∴点M必在直线 x=3 上.
记直线 x=3 与x轴交于点 H(3,0) ,
∵ OM=OA=2,OH=3 ,
∴ MH=OM2-OH2=1 , ∠MOH=30° .
分两种情况:
a)如图,当点M在x轴上方时,点M恰为 (3,1) ,符合题意,此时 ∠AOM=60°,α=60° ;
b)如图,当点M在x轴下方时,点M为 (3,-1) ,由 MN=2 知点N为 (3,1) ,也符合题意,此时 ∠AOM=120°,α=120° .
综上, α 的值为 60° 或 120° .
(2)当0
∴不符合题意
综上所述, 22
∴ △DAB , △DBC 为等边三角形
∴由三线合一知, DE=AD2+(AB2)2=m2+(m2)2=32m
∵ DE⊥AB , DF⊥BC
∴ ∠DBE=∠DFB=90°
又 DB=DB
∴ △DEB≌△DFB
∴ DE=DF=32m
(2)解: HB=3HG
证明:延长 GH 交 DE 于点 M ,连接 MB
由题意知 ∠1=∠ACB=30° , ∠2=∠3=60°
∵ FG//DE
∴ ∠3=∠AGF=∠GCB+∠GFC=60° , ∠HFG=∠HDM
∴ ∠GFC=∠GCF=30°
∴ GF=GC
∵ H 为 DC 的中点
∴ HF=HD
∵ ∠GHF=∠MHD
∴ △HGF≌△HMD
∴ GF=MD , HM=HG
∴ MD=CG
在 △DMB 和 △CGB 中
{∠MDB=∠GCB=30°MD=GCDB=CB
∴ △DMB ≌ △CGB
∴ BM=BG , ∠MBD=∠GBC
∴ ∠MBG=∠DBC=60°
∴ △MBG 为等边三角形
∴ BH⊥MG
∴ HB=3HG
(3)解: HF=36m
作 △BHC 关于点 B 顺时旋转 60° ,得到 △BH'C' ,
∴ △BHH' 为等边三角形
∴ HB+HC+HD=HD+HH'+H'C'
当点 D , H , H' , C' 四点共线时, HD+HH'+H'C' 值最小
连接 CC'
此时有 BC=BC' , ∠CBC'=60°
∴ △BCC' 为等边三角形
∵ DB=DC , C'B=C'C
∴ DC' 为 BC 的垂直平分线
∴ BF 垂直平分 HH'
∴ ∠HBF=∠FBH'=30°
∴ HF= false
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
