1.2矩形的性质与判定 新思维同步提高训练(Word版含解答)-2021-2022学年九年级数学北师大版上册
文档属性
| 名称 | 1.2矩形的性质与判定 新思维同步提高训练(Word版含解答)-2021-2022学年九年级数学北师大版上册 |  | |
| 格式 | docx | ||
| 文件大小 | 329.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 13:14:27 | ||
图片预览


文档简介
1.2矩形的性质与判定 新思维同步提高训练(Word版含解答)-2021-2022学年九年级数学北师大版上册
一、选择题
1.如图,矩形纸片ABCD中,点E是AD的中点,且AE=2,BE的垂直平分线MN恰好过点C,则矩形的一边AB的长度为( ???)
A.?2???????????????????????B.?2 5?????????????????????C.?4?????????????????????????D.?2 3
2.如图,已知在矩形ABCD中,M是AD边中点,将矩形分别沿MN、MC折叠,A、D两点刚好落在点E处,已知AN=3,MN=5,设BN=x,则x的值为(?? )
A.?53????????????????????????B.?73??????????????????????????C.?52???????????????????????????D.?94
3.如图,在平行四边形 ABCD 中,M、N是 BD 上两点, BM=DN ,连接 AM 、 MC 、 CN 、 NA ,添加一个条件,使四边形 AMCN 是矩形,这个条件是(??? )
A.?∠AMB=∠CND????????B.?MB=MO????????C.?BD⊥AC?????????????D.?AC=2OM
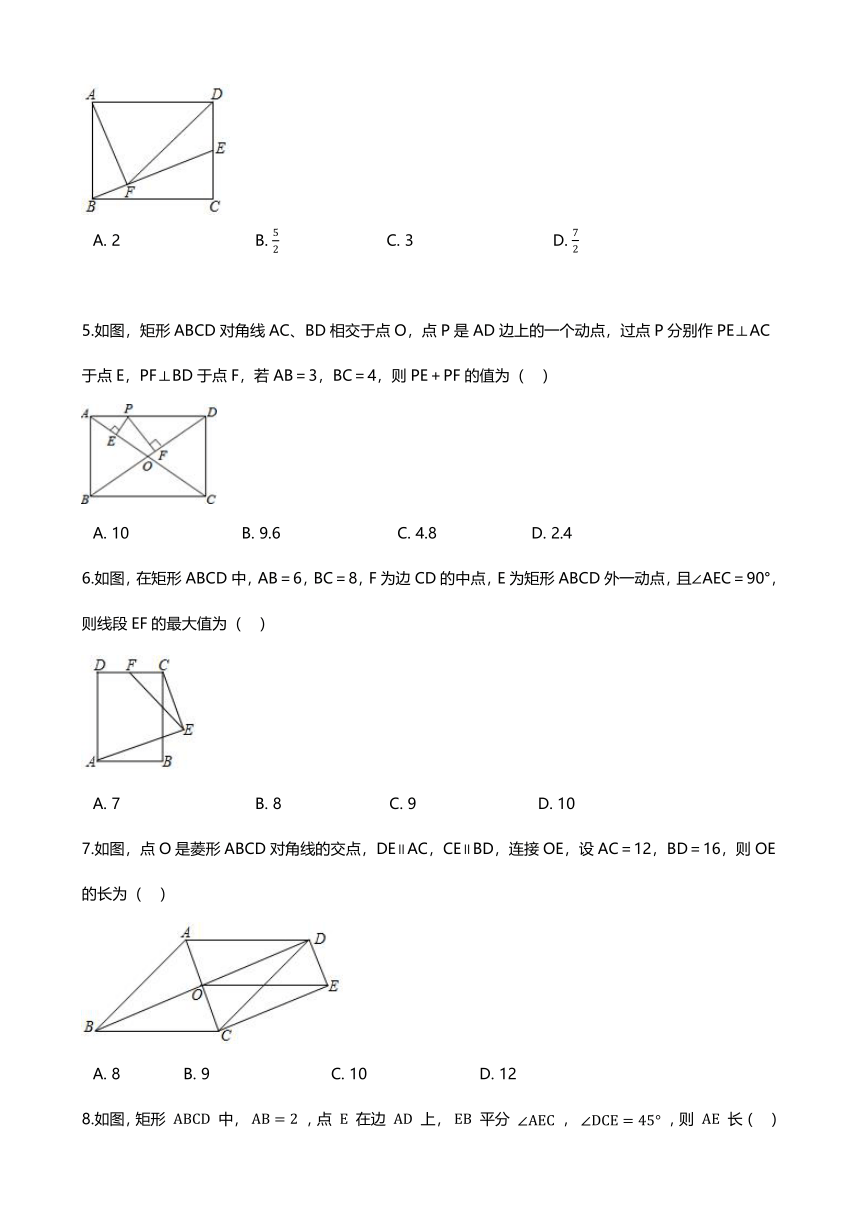
4.如图,点E是矩形ABCD的边CD上一点,作AF⊥BE于F,连接DF,若AB=6,DF=BC,则CE的长度为(?? )
A.?2??????????????????????????????B.?52????????????????????????C.?3???????????????????????????????D.?72
5.如图,矩形ABCD对角线AC、BD相交于点O,点P是AD边上的一个动点,过点P分别作PE⊥AC于点E,PF⊥BD于点F,若AB=3,BC=4,则PE+PF的值为(?? )
A.?10?????????????????????????B.?9.6??????????????????????????C.?4.8?????????????????????D.?2.4
6.如图,在矩形ABCD中,AB=6,BC=8,F为边CD的中点,E为矩形ABCD外一动点,且∠AEC=90°,则线段EF的最大值为(?? )
A.?7??????????????????????????????B.?8????????????????????????C.?9???????????????????????????D.?10
7.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为(?? )
A.?8??????????????B.?9???????????????????????????C.?10?????????????????????????D.?12
8.如图,矩形 ABCD 中, AB=2 ,点 E 在边 AD 上, EB 平分 ∠AEC , ∠DCE=45° ,则 AE 长(?? )
A.?2?????????????????B.?22-2????????????????????C.?2-2??????????????????????D.?2
9.如图是一个由5张纸片拼成的 ?ABCD ,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为 S1 ,另两张直角三角形纸片的面积都为 S2 ,中间一张矩形纸片 EFGH 的面积为 S3 , FH 与 GE 相交于点O.当 △AEO,△BFO,△CGO,△DHO 的面积相等时,下列结论一定成立的是(?? )
A.?S1=S2?????????????B.?S1=S3???????????????????C.?AB=AD???????????????????D.?EH=GH
10.如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 5 .
以上结论中,你认为正确的有(? )个.
A.?1??????????????????????????B.?2?????????????????????????????C.?3???????????????????????D.?4
二、填空题
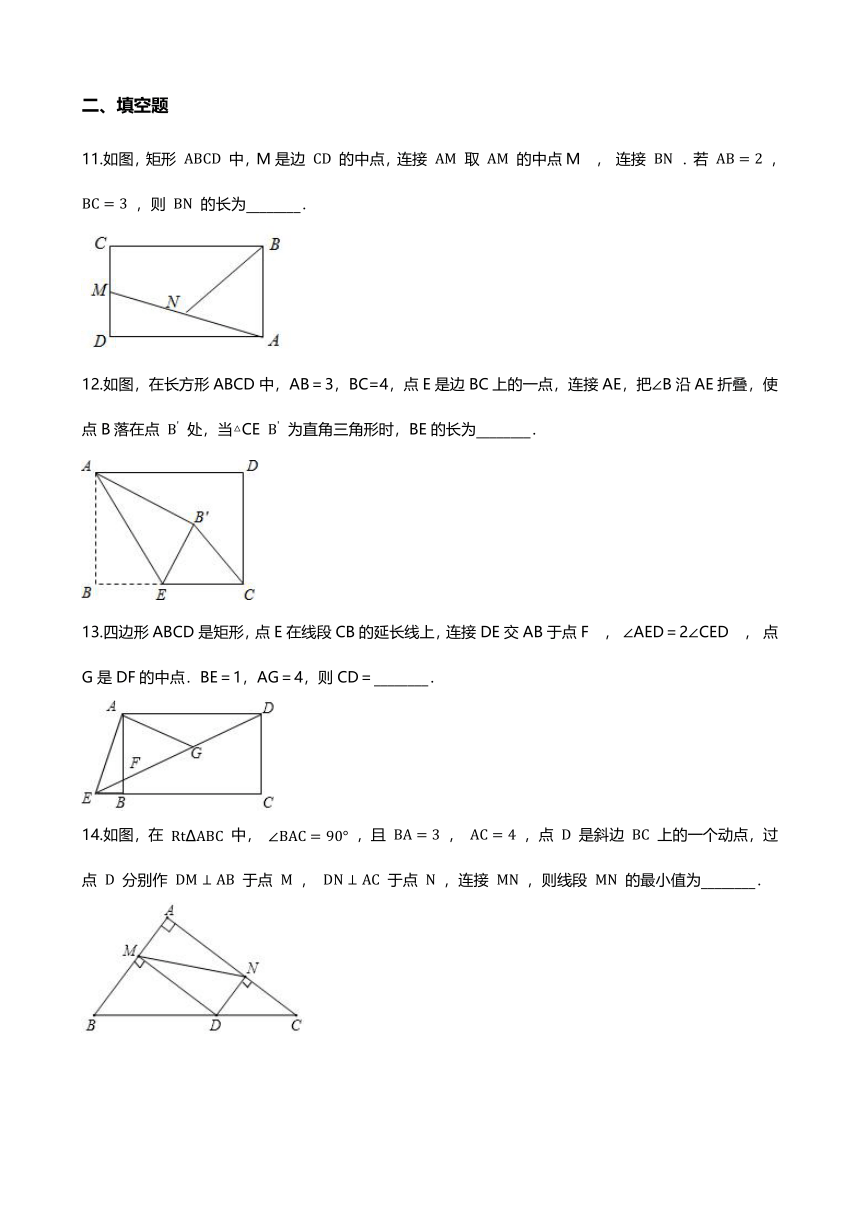
11.如图,矩形 ABCD 中,M是边 CD 的中点,连接 AM 取 AM 的中点M , 连接 BN .若 AB=2 , BC=3 ,则 BN 的长为________.
12.如图,在长方形ABCD中,AB=3,BC=4,点E是边BC上的一点,连接AE,把∠B沿AE折叠,使点B落在点 B' 处,当△CE B' 为直角三角形时,BE的长为________.
13.四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F , ∠AED=2∠CED , 点G是DF的中点.BE=1,AG=4,则CD=________.
14.如图,在 RtΔABC 中, ∠BAC=90° ,且 BA=3 , AC=4 ,点 D 是斜边 BC 上的一个动点,过点 D 分别作 DM⊥AB 于点 M , DN⊥AC 于点 N ,连接 MN ,则线段 MN 的最小值为________.
15.如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°.某班学习委员得到四个结论:①DC=3OG;②OG= 12 BC;③ △ OGE是等边三角形;④S△AOE= 16 S矩形ABCD , 问:学习委员得到结论正确的是________.(填写所有正确结论的序号)
16.如图,在矩形 ABCD 中, BC=16 , E 为 CD 上一点,将 △BCE 沿 BE 折叠,使点 C 正好落在 AD 边上的 F 处,作 ∠ABF 的平分线交 AD 于 N ,交 EF 的延长线于 M ,若 NF=12BC ,则 AB 的长为 ________ .
三、解答题
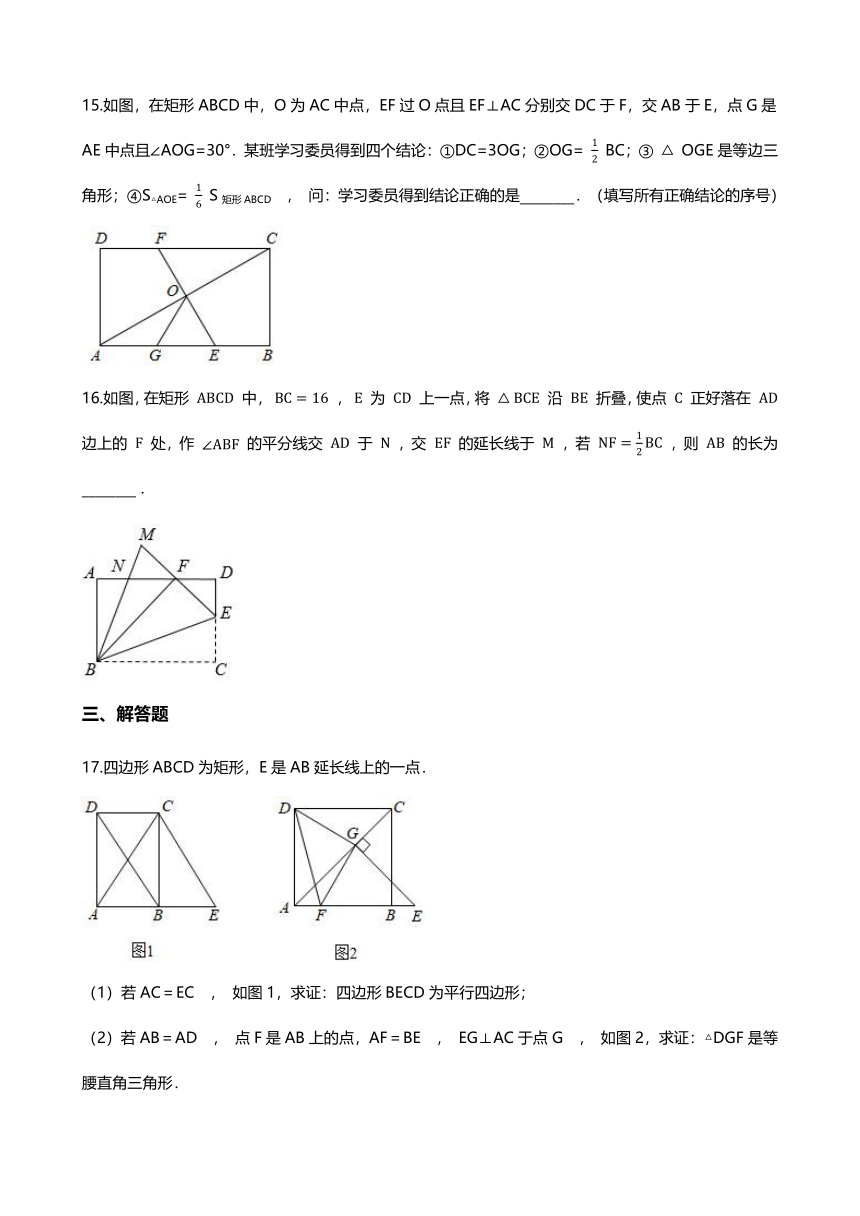
17.四边形ABCD为矩形,E是AB延长线上的一点.
(1)若AC=EC , 如图1,求证:四边形BECD为平行四边形;
(2)若AB=AD , 点F是AB上的点,AF=BE , EG⊥AC于点G , 如图2,求证:△DGF是等腰直角三角形.
18.如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(﹣8,0),直线BC经过点B(﹣8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转角度α得到四边形OA′B′C′,此时边OA′与边BC交于点P,边B′C′与BC的延长线交于点Q,连接AP.
(1)四边形OABC的形状是________.
(2)在旋转过程中,当∠PAO=∠POA,求P点坐标.
(3)在旋转过程中,当P为线段BQ中点时,连接OQ,求△OPQ的面积.
19.如图,菱形ABCD的对角线AC、BD相交于点O,分别过A、D两点作AO、DO的垂线,两垂线交于点E。
(1)求证:四边形AODE是矩形;
(2)若∠DAE=60°,AD=6,求BD的长。
20.如图,四边形 ABCD 为矩形,G是对角线 BD 的中点.连接 GC 并延长至F,使 CF=GC ,以 DC 、 CF 为邻边作 ?DCFE ,连接 CE .
(1)若四边形 DCFE 是菱形,判断四边形 CEDG 的形状,并证明你的结论.
(2)在(1)条件下,连接 DF ,若 BC=3 ,求 DF 的长.
21.探索与应用:如图
(1)问题解决:如图1.在平行四边形纸片ABCD(AD>AB)中,将纸片沿过点A的直线折叠,使点B落在AD上的点 B' 处,折线AE交BC于点E,连接B'E.求证:四边形 ABEB' 是菱形.
(2)规律探索:如图2,在平行四边形纸片ABCD(AD>AB)中,将纸片沿过点P的直线折叠,点B恰好落在AD上的点Q处,点A落在点A′处,得到折痕FP,那么△PFQ是等腰三角形吗?请说明理由.
(3)拓展应用:如图3,在矩形纸片ABCD(AD>AB)中,将纸片沿过点P的直线折叠,得到折痕FP,点B落在纸片ABCD内部点 B' 处,点A落在纸片ABCD外部点 A' 处, A'B' 与AD交于点M,且 A' M= B' M.已知:AB=4,AF=2,求BP的长.
22.将一矩形纸片 OABC 放在直角坐标系中, O 为原点, C 在 x 轴上, OA=9 , OC=15 .
(1)如图1,在 OA 上取一点 E ,将 △EOC 沿 EC 折叠,使 O 点落至 AB 边上的 D 点,求直线 EC 的解析式;
(2)如图2,在 OA 、 OC 边上选取适当的点 M 、 F ,将 △MOF 沿 MF 折叠,使 O 点落在 AB 边上的 D' 点,过 D' 作 DG⊥CO 于点 G 点,交 MF 于 T 点.
①求证: TG=AM ;
②设 T(x,y) ,探求 y 与 x 满足的等量关系式,并将 y 用含 x 的代数式表示(指出变量 x 的取值范围);
(3)在(2)的条件下,当 x=6 时,点 P 在直线 MF 上,问坐标轴上是否存在点 Q ,使以 M 、 D' 、 Q 、 P 为顶点的四边形是平行四边形,若存在,请直接写出 Q 点坐标;若不存在,请说明理由.
23.在平面直角坐标系中,O为原点,四边形 OABC 是矩形,点A,C的坐标分别是 (3,0) , (0,1) .点D是边 BC 上的动点(与端点B,C不重合),过点D作直线 y=-12x+b 交边 OA 于点E .
(1)如图①,直接写出D,E两点的坐标(用含b的式子表示).
(2)如图②,若矩形 OABC 关于直线 DE 的对称图形为矩形 O1A1B1C1 ,试探究矩形 O1A1B1C1 与距形 OABC 的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积:若改变,请说明理由;
(3)矩形 OABC 绕着它的对称中心旋转,如果旋转前后两矩形重叠部分的图形是菱形,请直接写出这个菱形面积的最大值和最小值.
答案
一、选择题
1.解:连接EC,
∵矩形ABCD,点E是AD的中点,AE=2
∴AD=BC=2AE=4,DE=AE=2,∠D=90°,
∵BE的垂直平分线MN恰好过点C,
∴CE=BC=4,
在Rt△CDE中,
AB=CD=CE2-DE2=42-22=23.
故答案为:D.
2.解:∵四边形ABCD是矩形,
∴∠A=90°,AB=CD,AD=BC,
∵AN=3,MN=5,
∴AM= MN2-AN2=52-32 =4,
∵M是AD边中点,
∴AM=DM=4,BC=8,
∵将矩形分别沿MN、MC折叠,A、D两点刚好落在点E处,
∴AN=NE=3,CE=CD,
∵BN2+BC2=CN2 ,
∴x2+82=(x+6)2 ,
解得x= 73 .
故答案为:B.
3.证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
∵对角线BD上的两点M、N满足BM=DN,
∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵2OM=AC,
∴MN=AC,
∴四边形AMCN是矩形.
故答案为:D.
4.解:过D作DH⊥AF于点H,延长DH与AB相交于点G,
∵四边形ABCD为矩形,
∴AD=BC,
∵DF=BC,
∴DA=DF,
∴AH=FH,
∵AF⊥BE,
∴DG∥BE,
∴GH为△ABF的中位线,
∴AG=BG= 12 AB=3,
∵矩形ABCD中,AB=DC=6,AB∥DC,
∴四边形BEDG为平行四边形,
∴DE=BG=3,
∴CE=CD-DE=6-3=3.
故答案为:C.
5.解:连接OP,
∵矩形ABCD的两边AB=3,BC=4,
∴S矩形ABCD=AB?BC=12,OA=OC,OB=OD,AC=BD,AC= AB2+BC2 =5,
∴S△AOD= 14 S矩形ABCD=3,OA=OD= 52 ,
∴S△AOD=S△AOP+S△DOP= 12 OA?PE+ 12 OD?PF= 12 OA(PE+PF)= 12 × 52 ×(PE+PF)=3,
∴PE+PF= 125 =2.4.
故答案为:D.
6.解:如图,连接AC,取AC的中点O,连结OF,OE,
∵矩形ABCD中,AB=6,BC=8,∠B=90°,F为CD的中点,
∴AC= AB2+BC2=62+82=10 ,
∵AO=OC,CF=FD,
∴OF= 12 AD= 12 BC=4,
∵∠AEC=90°,
∴OE= 12 AC= 12×10 =5,
由三角形的三边关系得,O、E、F三点共线时EF最大,
此时EF最大=4+5=9.
故答案为:C.
7.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD, OA=OC=12AC=6,OB=OD=12BD=8,
∴∠DOC=90°, CD=OC2+OD2=62+82=10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故答案为:C.
8.解:∵四边形ABCD是矩形,
∴AB=CD=2,∠A=∠D=∠DCB=90°,
∵∠DCE=45°,
∴DE=DC=2,
∴EC=2 2 ,
∵∠DCE=45°,
∴∠DEC=45°,
∵EB平分∠AEC,
∴∠AEB=∠BEC= 12 ∠AEC= 180°-45°2 =67.5°,
∵AD∥BC
∴∠AEB=∠EBC,
∴∠BEC=∠EBC,
∴BC=CE=2 2 ,
∴AD=BC=2 2 ,
∴AE=AD-DE=2 2 -2,
故答案为:B.
9.解:由题意得,△AED和△BCG是等腰直角三角形,
∴ ∠ADE=∠DAE=∠BCG=∠GBC=45°
∵四边形ABCD是平行四边形,
∴AD=BC,CD=AB,∠ADC=∠ABC,∠BAD=∠DCB
∴∠HDC=∠FBA,∠DCH=∠BAF,
∴△AED≌△CGB,△CDH≌ABF
∴AE=DE=BG=CG
∵四边形HEFG是矩形
∴GH=EF,HE=GF
设AE=DE=BG=CG=a, HE=GF= b ,GH=EF= c
过点O作OP⊥EF于点P,OQ⊥GF于点Q,
∴OP//HE,OQ//EF
∵点O是矩形HEFG的对角线交点,即HF和EG的中点,
∴OP,OQ分别是△FHE和△EGF的中位线,
∴ OP=12HE=12b , OQ=12EF=12c
∵ SΔBOF=12BF·OQ=12(a-b)×12c=14(a-b)c
SΔAOE=12AE·OP=12a×12b=14ab ?
∵ SΔBOF=SΔAOE
∴ 14(a-b)c=14ab ,即 ac-bc=ab
而 S1=SΔAED=12AE·DE=12a2 ,
S2=SΔAFB=12AF·BF=12(a+c)(a-b)=12(a2-ab+ac-bc)=12(a2-ab+ab)=12a2 ?
所以, S1=S2 ,A符合题意,
S3=HE·EF=(a-b)(a+c)=a2-bc-ab+ac=a2+ab-ab=a2 ?
∴ S1≠S3 ,B不符合题意,
而 AB=AD 于 EH=GH 都不一定成立,故 C,D 都不符合题意,
故答案为:A
10.解:∵将纸片ABCD沿直线EF折叠,
∴FC=FH,∠HFE=∠CFE,
∵AD∥BC,
∴∠HEF=∠EFC=∠HFE,HE∥FC,
∴△HFE为等腰三角形,
∴HE=HF=FC,
∵EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴EH∥CF,且HE =FC,
∴四边形CFHE是平行四边形,
∵FC=FH,
∴四边形CFHE是菱形,
故①符合题意;
∵HC为菱形的对角线,
∴∠BCH=∠ECH,∠BCD=90°,
∴只有∠DCE=30°时EC平分∠DCH,
故②不符合题意;
过点F作FM⊥AD于M,
点H与点A重合时,BF最小,设BF=x,则AF=FC=8﹣x,
在Rt△ABF中,AB2+BF2=AF2 ,
即42+x2=(8﹣x)2 ,
解得x=3,
点G与点D重合时,点H与点M重合,BF最大,CF=FM=DM=CD=4,
∴BF=4,
∴线段BF的取值范围为3≤BF≤4,
故③符合题意;
当点H与点A重合时,由③中BF=3,
∴AF=AE=CF=EC=8-3=5,
则ME=5﹣3=2,
由勾股定理得,
EF= MF2+ME2=42+22 =2 5 ,
故④符合题意;
综上所述,结论正确的有①③④共3个.
故答案为:C.
二、填空题
11.如下图:
过点N作 GH//AB ,分别交BC于点G , 交AD于点H , 易得 GH//CD , GH=AB=CD ,
∵四边形ABCD是矩形
∴ ∠C=∠D=90? , AB//DC , AB=CD , AD=BC ,
在 Rt△AMD 中,点N是线段AM中点,点M、点N分别在线段CD、GH上,
∴ NH=12MD ,
又∵M是CD的中点,
∴MD=12CD=12AB=1 ,
∴NH=12MD=1×12=12 ,
∴GN=GH-NH=2-12=32 ,
∵ GH//CD , ∠C=90? ,
∴ ∠BGN=90? ,
在 Rt△BGN 中, BG=AH=12BC=32 , GN=32 ,
∴BN=2GN=2×32=322 .
故答案为: 322
12.解:当 ΔCEB' 为直角三角形时,有两种情况:
①当点 B' 落在矩形内部时,如答图1所示.
连结 AC ,
在 RtΔABC 中, AB=3 , BC=4 ,
∴AC=42+32=5 ,
∵∠B 沿 AE 折叠,使点 B 落在点 B' 处,
∴∠AB'E=∠B=90° ,
当 ΔCEB' 为直角三角形时,只能得到 ∠EB'C=90° ,
∴ 点 A 、 B' 、 C 共线,即 ∠B 沿 AE 折叠,使点 B 落在对角线 AC 上的点 B' 处,
∴EB=EB' , AB=AB'=3 ,
∴CB'=5-3=2 ,
设 BE=x ,则 EB'=x , CE=4-x ,
在 RtΔCEB' 中,
∵EB'2+CB'2=CE2 ,
∴x2+22=(4-x)2 ,解得 x=32 ,
∴BE=32 ;
②当点 B' 落在 AD 边上时,如答图2所示.
此时 ABEB' 为正方形,
∴BE=AB=3 .
综上所述, BE 的长为 32 或3.
故答案为: 32 或3.
13.解: ∵ 四边形ABCD是矩形,点G是DF的中点.
∴∠DAF=90°,AG=DG,AD//BC, ?
∴∠GAD=∠GDA, ?
∴ ?∠AGE=∠ADG+∠DAG=2∠DAG ,
∵AD//BC, ?
∴∠ADG=∠DEC, ?
又∵∠AED=2∠CED ,
∴∠AED=∠AGE ,
∴AE=AG ,
∵AG=4,
∴AE=4,
∵四边形ABCD为矩形,
∴∠BAD=∠ABC=90°,
在Rt△AEB中,由勾股定理可求AB= AE2-BE2=42-12 = 15 ,
∴CD= AB= 15 ,
故答案为: 15 .
14.解:∵ ∠BAC=90° ,且 BA=3 , AC=4 ,∴ BC=BA2+AC2=5 ,
∵ DM⊥AB , DN⊥AC ,∴ ∠DMA=∠DNA=∠BAC=90° ,
∴四边形 DMAN 是矩形.
如图,连接AD , 则 MN=AD ,
∴当 AD⊥BC 时, AD 的值最小,此时, ΔABC 的面积 =12AB×AC=12BC×AD ,
∴ AD=AB×ACBC=125 ,∴ MN 的最小值为 125 ;
故答案为 125 .
15.解:∵ EF⊥AC ,点 G 是 AE 中点,
∴ OG=AG=GE=12AE ,
∵ ∠AOG=30° ,
∴ ∠OAG=∠AOG=30° ,
∠GOE=90°-30°=60° ,
∴ △OGE 是等边三角形,故③符合题意;
设 AE=2a ,则 OE=OG=a ,
由勾股定理得, AO=AE2-OE2=(2a)2-a2=3a ,
∵ O 为 AC 中点,
∴ AC=2AO=23a ,
∴ BC=12AC=12×23a=3a ,
在 Rt△ABC 中,由勾股定理得, AB=(23a)2-(3a)2=3a ,
四边形 ABCD 是矩形,
∴ CD=AB=3a ,
∴ DC=3OG ,故①符合题意;
∵ OG=a , BC=3a , 12BC=32a ,
∴ OG≠12BC ,故②不符合题意;
∵ S△AOE=12a?3a=32a2 ,
SABCD=3a?3a=33a2 ,
∴ S△AOE=16SABCD ,故④符合题意;
综上所述,结论符合题意是①③④,
故答案为:①③④.
16.解:∵将 △BCE 沿 BE 折叠得 △BFE ,
∴ BC=BF ,
如图示,过点 N 作 NG⊥BF 交 BF 于点 G ,
∵ AN 是 ∠ABF 的平分线
∴ AN=NG ,
又∵ S△NFB=12BF·NG=12NF·AB , NF=12BC=12×16=8 ,
可得: BF·AN=12BC·AB ,即 AN=12AB ,
设 AB=2x ,则 AN=x , AF=AN+NF=x+8 ,
在 Rt△ABF 中, AB2+AF2=BF2 ,
即: (2x)2+(x+8)2=162 ,
解之得: x=245 ,负值已舍去,
∴ AB=485 ,
故答案为: 485 .
三、解答题
17. (1)证明:∵四边形ABCD为矩形,
∴AB∥CD,AB=CD,CB⊥AE,
又∵AC=EC,
∴AB=BE,
∴BE=CD,BE∥CD,
∴四边形BECD为平行四边形
(2)证明:∵AB=AD,
∴矩形ABCD是正方形,
∵EG⊥AC,
∴∠E=∠GAE=45°,
∴GE=GA,
又∵AF=BE,
∴AB=FE,
∴FE=AD,
在△EGF和△AGD中,
{GE=GA∠E=∠DAC=45?EF=AD ,
∴△EGF≌△AGD(SAS),
∴GF=GD,∠DGA=∠FGE,
∠DGF=∠DGA+∠AGF=∠EGF+∠AGF=∠AGE=90°,
∴△DGF是等腰直角三角形
18.(1)矩形
(2)解:如图1,过点P作PE⊥AO于点E,
∵∠PAO=∠POA,
∴PA=PO,
∵PE⊥AO,
∴AE=EO=4,
∴P(﹣4,6);
(3)解:如图2,在Rt△OCQ和Rt△OC'Q中,
{CO=C'OOQ=OQ ,
∴Rt△OCQ≌Rt△OC'Q(HL),
∴∠OQC=∠OQC',
又∵OP∥C'Q,
∵∠POQ=∠OQC',
∴∠POQ=∠PQO,
∴PO=PQ,
∵BP=QP,
∴BP=OP=x,
在Rt△OPC中,x2=(8﹣x)2+62 ,
解得:x= 254 .
故S△OPQ= 12 ×CO×PQ= 12×6×254=754 .
(1)∵点A的坐标为(﹣8,0),点B(﹣8,6),C(0,6),
?
∴∠COA=∠OAB=∠B=90°,
∴四边形OABC是矩形.
故答案为矩形;
19. (1)证明:∵四边形ABCD是菱形,∴AC上BD,∠AOD=90°∵EA⊥AO,DE⊥DO,∴∠EAO=∠EDO= 90°,∴四边形AODE是矩形.
(2)解:∵四边形AODE是矩形,∴∠DOA =∠EAO= 90°∵∠DAE = 60°,AD
= 6,∴∠DAO=30°,DO= 12 AD=3,∴BD=6
20. (1)解:四边形 CEDG 是菱形,理由如下:
∵四边形 ABCD 为矩形,G是对角线 BD 的中点,
∴ GB=GC=GD ,
∵ CF=GC ,
∴ GB=GC=GD=CF ,
∵四边形 DCFE 是菱形,
∴ CD=CF=DE , DE//CG ,
∴ DE=GC ,
∴四边形 CEDG 是平行四边形,
∵ GD=GC ,
∴四边形 CEDG 是菱形
(2)解:∵ CD=CF , GB=GD=GC=CF ,
∴ △CDG 是等边三角形,
∴ CD=BG , GCD=∠DGC=60° ,
∴ ∠DCF=∠BGC=120° ,
∴ △BGC≌△DCF(SAS) ,
∴ DF=BC=3 .
21. (1)解:由平行四边形的性质可知 AD//BC ,
∴ ∠AB'E=∠CEB' ,
由翻折可知 ∠AB'E=∠ABE ,
∴ ∠CEB'=∠ABE ,
∴ AB//B'E .
∴四边形 ABEB' 是平行四边形.
再由翻折可知 AB'=AB ,
∴四边形 ABEB' 是菱形
(2)解:由翻折可知 ∠BPF=∠QPF ,
∵ AD//BC ,
∴ ∠BPF=∠QFP ,
∴ ∠QPF=∠QFP ,
∴QF=QP,
∴ △PFQ 是等腰三角形
(3)解:如图,延长 PB' 交AD于点G,
根据题意可知 ∠FA'M=∠GB'M=90° ,
在 △FA'M 和 △GB'M 中, {∠FA'M=∠GB'M=90°A'M=B'M∠FMA'=∠GMB' ,
∴ △FA'M?△GB'M(ASA) ,
∴ A'F=B'G=AF=2 , FM=GM .
根据(2)同理可知 △PFG 为等腰三角形.
∴FG=PG.
∵ A'F=AM=2 ,
∴在 Rt△A'FM 中, FM=A'M2+A'F2=22 ,
∴ FG=2FM=42 ,
∴ PG=42 ,
∴ PB=PB'=PG-B'G=42-2 .
22. (1)解:如图1中,
∵ OA=9 , OC=15 ,
∵ △DEC 是由 △OEC 翻折得到,
∴ CD=OC=15 ,
在 Rt△DBC 中, DB=DC2-BC2=12 ,
∴ AD=3 ,设 OE=ED=x ,
在 Rt△DBC 中, x2=(9-x)2+32 ,
解得 X=5 ,
∴ E(0,5) ,
设直线 EC 的解析式为 y=kx+5 ,把 (15,0) 代入得到 k=-13 ,
∴直线 EC 的解析式为 y=-13x+5
(2)解:①证明:如图2中,
∵ MD'=MO , ∠D'MN=∠OMN ,
∵ OM//GD' ,
∴ ∠OMT=∠D'TM ,
∴ ∠D'MT=∠D'TM ,
∴ D'M=D'T ,
∴ OM=DT ,
∵ OA=DG ,
∴ AM=TG .
②如图3中,连接 OT ,
由(2)可得 OT=D'T ,
由勾股定理可得 x2+y2=(9-y)2 ,
得 y=-118x2+92 .
结合(1)可得 AD'=OG=3 时, x 最小,从而 x≥3 ,
当 MN 恰好平分 ∠OAB 时, AD' 最大即 x 最大,
此时 G 点与 N 点重合,四边形 AOND' 为正方形,
故 x 最大为9.从而 x≤9 ,
∴ 3≤x≤9
(3)解:如图4中, x=6 时, y=52 ,即点 T 坐标 (6,52) .
∴ OM=D'T=9-52=132 ,
①当 MD' 为对角线时,点 P 与 T 重合, QM=D'T=132 ,
∴ OQ=13 ,
∴此时点 Q 坐标 (0,13) .
② D'M 为边时,∵四边形 MD'QP 是平行四边形,
又∵四边形 D'MOT 是平行四边形,
∴点 P 与 T 重合,点 Q 与点 O 重合,
∴点 Q 坐标 (0,0) ,
③当点 P″ 在第四象限点时,四边形 MD'Q″P″ 是平行四边形时,
∵直线 NM 的解析式为 y=-23x+132 ,
∵ D'Q″//MN ,
∴直线 D'Q″ 的解析式为 y=-23x+13 ,
当 y=0 时, x=392 ,Q″(392,0)
综上所述,以 M 、 F 、 Q 、 P 为顶点的四边形是平行四边形时,点 Q 坐标 (0,0) 或 (0,13) 或 (392,0)
23.(1)解: D(2b-2,1) ; E(2b,0)
(2)解: CB 与 O1A1 的交点为M, C1B1 与 OA 的交点为N,如图:
∵ 四边形 OABC ,四边形 O1A1B1C1 是矩形,
∴CB//OA , C1B1//O1A1 ,
∴ 四边形 DMEN 是平行四边形,
∵ 矩形 OABC 关于直线 DE 的对称图形为矩形 O1A1B1C1 ,
∴∠1=∠2 ,
∵CB//OA ,
∴∠2=∠3 ,
∴∠1=∠3 ,
∴DM=ME ,
∴ 平行四边形 DMEN 是菱形,
过点D作 DH⊥OA 于点H,
由 D(2b-2,1) , E(2b,0) ,
可知 CD=2b-2 , OE=2b , OH=CD=2b-2 ,
∴EH=OE-OH=2b-(2b-2)=2 ,
设菱形 DMEN 的边长为 m ,
在 Rt△DHN 中, DH=1 , HN=EH-NE=2-m , DN=m ,
由 DH2+HN2=DN2 ,得 12+(2-m)2=m2 ,
解得: m=54 ,
∴ S菱形DMEN=NE?DH=54×1=54 ,
所以重叠部分菱形 DMEN 的面积不变, 为 54 ;
(3)S最大=53 ; S最小=1
解:(1) ∵ 四边形 OABC 是矩形,
?
∴CB//x 轴,
由点A,C的坐标分别为 (3,0) , (0,1) .
可得点D的纵坐标为 1 ,
当 y=1 时, y=-12x+b ,
解得: x=2b-2 ,
∴D 的坐标为 (2b-2,1)
当 y=0 时, y=-12x+b ,
解得: x=2b ,
∴E 的坐标为 (2b,0)
(3) 如下图所示,
当这个菱形 DNEM 是正方形时,即 NE=1 时,菱形的面积最小,最小值是1;
如下图所示,
当这个菱形A与E重合时,菱形 CNAM 的面积最大,
设 CN=AN=x ,则 ON=AO-AN=3-x ,
Rt△CON 中, 12+(3-x)2=x2
解之得: x=53 ,
∴ AN=53
∴菱形面积的最大值是 AN·CO=1×53=53 .
一、选择题
1.如图,矩形纸片ABCD中,点E是AD的中点,且AE=2,BE的垂直平分线MN恰好过点C,则矩形的一边AB的长度为( ???)
A.?2???????????????????????B.?2 5?????????????????????C.?4?????????????????????????D.?2 3
2.如图,已知在矩形ABCD中,M是AD边中点,将矩形分别沿MN、MC折叠,A、D两点刚好落在点E处,已知AN=3,MN=5,设BN=x,则x的值为(?? )
A.?53????????????????????????B.?73??????????????????????????C.?52???????????????????????????D.?94
3.如图,在平行四边形 ABCD 中,M、N是 BD 上两点, BM=DN ,连接 AM 、 MC 、 CN 、 NA ,添加一个条件,使四边形 AMCN 是矩形,这个条件是(??? )
A.?∠AMB=∠CND????????B.?MB=MO????????C.?BD⊥AC?????????????D.?AC=2OM
4.如图,点E是矩形ABCD的边CD上一点,作AF⊥BE于F,连接DF,若AB=6,DF=BC,则CE的长度为(?? )
A.?2??????????????????????????????B.?52????????????????????????C.?3???????????????????????????????D.?72
5.如图,矩形ABCD对角线AC、BD相交于点O,点P是AD边上的一个动点,过点P分别作PE⊥AC于点E,PF⊥BD于点F,若AB=3,BC=4,则PE+PF的值为(?? )
A.?10?????????????????????????B.?9.6??????????????????????????C.?4.8?????????????????????D.?2.4
6.如图,在矩形ABCD中,AB=6,BC=8,F为边CD的中点,E为矩形ABCD外一动点,且∠AEC=90°,则线段EF的最大值为(?? )
A.?7??????????????????????????????B.?8????????????????????????C.?9???????????????????????????D.?10
7.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为(?? )
A.?8??????????????B.?9???????????????????????????C.?10?????????????????????????D.?12
8.如图,矩形 ABCD 中, AB=2 ,点 E 在边 AD 上, EB 平分 ∠AEC , ∠DCE=45° ,则 AE 长(?? )
A.?2?????????????????B.?22-2????????????????????C.?2-2??????????????????????D.?2
9.如图是一个由5张纸片拼成的 ?ABCD ,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为 S1 ,另两张直角三角形纸片的面积都为 S2 ,中间一张矩形纸片 EFGH 的面积为 S3 , FH 与 GE 相交于点O.当 △AEO,△BFO,△CGO,△DHO 的面积相等时,下列结论一定成立的是(?? )
A.?S1=S2?????????????B.?S1=S3???????????????????C.?AB=AD???????????????????D.?EH=GH
10.如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2 5 .
以上结论中,你认为正确的有(? )个.
A.?1??????????????????????????B.?2?????????????????????????????C.?3???????????????????????D.?4
二、填空题
11.如图,矩形 ABCD 中,M是边 CD 的中点,连接 AM 取 AM 的中点M , 连接 BN .若 AB=2 , BC=3 ,则 BN 的长为________.
12.如图,在长方形ABCD中,AB=3,BC=4,点E是边BC上的一点,连接AE,把∠B沿AE折叠,使点B落在点 B' 处,当△CE B' 为直角三角形时,BE的长为________.
13.四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F , ∠AED=2∠CED , 点G是DF的中点.BE=1,AG=4,则CD=________.
14.如图,在 RtΔABC 中, ∠BAC=90° ,且 BA=3 , AC=4 ,点 D 是斜边 BC 上的一个动点,过点 D 分别作 DM⊥AB 于点 M , DN⊥AC 于点 N ,连接 MN ,则线段 MN 的最小值为________.
15.如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°.某班学习委员得到四个结论:①DC=3OG;②OG= 12 BC;③ △ OGE是等边三角形;④S△AOE= 16 S矩形ABCD , 问:学习委员得到结论正确的是________.(填写所有正确结论的序号)
16.如图,在矩形 ABCD 中, BC=16 , E 为 CD 上一点,将 △BCE 沿 BE 折叠,使点 C 正好落在 AD 边上的 F 处,作 ∠ABF 的平分线交 AD 于 N ,交 EF 的延长线于 M ,若 NF=12BC ,则 AB 的长为 ________ .
三、解答题
17.四边形ABCD为矩形,E是AB延长线上的一点.
(1)若AC=EC , 如图1,求证:四边形BECD为平行四边形;
(2)若AB=AD , 点F是AB上的点,AF=BE , EG⊥AC于点G , 如图2,求证:△DGF是等腰直角三角形.
18.如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(﹣8,0),直线BC经过点B(﹣8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转角度α得到四边形OA′B′C′,此时边OA′与边BC交于点P,边B′C′与BC的延长线交于点Q,连接AP.
(1)四边形OABC的形状是________.
(2)在旋转过程中,当∠PAO=∠POA,求P点坐标.
(3)在旋转过程中,当P为线段BQ中点时,连接OQ,求△OPQ的面积.
19.如图,菱形ABCD的对角线AC、BD相交于点O,分别过A、D两点作AO、DO的垂线,两垂线交于点E。
(1)求证:四边形AODE是矩形;
(2)若∠DAE=60°,AD=6,求BD的长。
20.如图,四边形 ABCD 为矩形,G是对角线 BD 的中点.连接 GC 并延长至F,使 CF=GC ,以 DC 、 CF 为邻边作 ?DCFE ,连接 CE .
(1)若四边形 DCFE 是菱形,判断四边形 CEDG 的形状,并证明你的结论.
(2)在(1)条件下,连接 DF ,若 BC=3 ,求 DF 的长.
21.探索与应用:如图
(1)问题解决:如图1.在平行四边形纸片ABCD(AD>AB)中,将纸片沿过点A的直线折叠,使点B落在AD上的点 B' 处,折线AE交BC于点E,连接B'E.求证:四边形 ABEB' 是菱形.
(2)规律探索:如图2,在平行四边形纸片ABCD(AD>AB)中,将纸片沿过点P的直线折叠,点B恰好落在AD上的点Q处,点A落在点A′处,得到折痕FP,那么△PFQ是等腰三角形吗?请说明理由.
(3)拓展应用:如图3,在矩形纸片ABCD(AD>AB)中,将纸片沿过点P的直线折叠,得到折痕FP,点B落在纸片ABCD内部点 B' 处,点A落在纸片ABCD外部点 A' 处, A'B' 与AD交于点M,且 A' M= B' M.已知:AB=4,AF=2,求BP的长.
22.将一矩形纸片 OABC 放在直角坐标系中, O 为原点, C 在 x 轴上, OA=9 , OC=15 .
(1)如图1,在 OA 上取一点 E ,将 △EOC 沿 EC 折叠,使 O 点落至 AB 边上的 D 点,求直线 EC 的解析式;
(2)如图2,在 OA 、 OC 边上选取适当的点 M 、 F ,将 △MOF 沿 MF 折叠,使 O 点落在 AB 边上的 D' 点,过 D' 作 DG⊥CO 于点 G 点,交 MF 于 T 点.
①求证: TG=AM ;
②设 T(x,y) ,探求 y 与 x 满足的等量关系式,并将 y 用含 x 的代数式表示(指出变量 x 的取值范围);
(3)在(2)的条件下,当 x=6 时,点 P 在直线 MF 上,问坐标轴上是否存在点 Q ,使以 M 、 D' 、 Q 、 P 为顶点的四边形是平行四边形,若存在,请直接写出 Q 点坐标;若不存在,请说明理由.
23.在平面直角坐标系中,O为原点,四边形 OABC 是矩形,点A,C的坐标分别是 (3,0) , (0,1) .点D是边 BC 上的动点(与端点B,C不重合),过点D作直线 y=-12x+b 交边 OA 于点E .
(1)如图①,直接写出D,E两点的坐标(用含b的式子表示).
(2)如图②,若矩形 OABC 关于直线 DE 的对称图形为矩形 O1A1B1C1 ,试探究矩形 O1A1B1C1 与距形 OABC 的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积:若改变,请说明理由;
(3)矩形 OABC 绕着它的对称中心旋转,如果旋转前后两矩形重叠部分的图形是菱形,请直接写出这个菱形面积的最大值和最小值.
答案
一、选择题
1.解:连接EC,
∵矩形ABCD,点E是AD的中点,AE=2
∴AD=BC=2AE=4,DE=AE=2,∠D=90°,
∵BE的垂直平分线MN恰好过点C,
∴CE=BC=4,
在Rt△CDE中,
AB=CD=CE2-DE2=42-22=23.
故答案为:D.
2.解:∵四边形ABCD是矩形,
∴∠A=90°,AB=CD,AD=BC,
∵AN=3,MN=5,
∴AM= MN2-AN2=52-32 =4,
∵M是AD边中点,
∴AM=DM=4,BC=8,
∵将矩形分别沿MN、MC折叠,A、D两点刚好落在点E处,
∴AN=NE=3,CE=CD,
∵BN2+BC2=CN2 ,
∴x2+82=(x+6)2 ,
解得x= 73 .
故答案为:B.
3.证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD
∵对角线BD上的两点M、N满足BM=DN,
∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵2OM=AC,
∴MN=AC,
∴四边形AMCN是矩形.
故答案为:D.
4.解:过D作DH⊥AF于点H,延长DH与AB相交于点G,
∵四边形ABCD为矩形,
∴AD=BC,
∵DF=BC,
∴DA=DF,
∴AH=FH,
∵AF⊥BE,
∴DG∥BE,
∴GH为△ABF的中位线,
∴AG=BG= 12 AB=3,
∵矩形ABCD中,AB=DC=6,AB∥DC,
∴四边形BEDG为平行四边形,
∴DE=BG=3,
∴CE=CD-DE=6-3=3.
故答案为:C.
5.解:连接OP,
∵矩形ABCD的两边AB=3,BC=4,
∴S矩形ABCD=AB?BC=12,OA=OC,OB=OD,AC=BD,AC= AB2+BC2 =5,
∴S△AOD= 14 S矩形ABCD=3,OA=OD= 52 ,
∴S△AOD=S△AOP+S△DOP= 12 OA?PE+ 12 OD?PF= 12 OA(PE+PF)= 12 × 52 ×(PE+PF)=3,
∴PE+PF= 125 =2.4.
故答案为:D.
6.解:如图,连接AC,取AC的中点O,连结OF,OE,
∵矩形ABCD中,AB=6,BC=8,∠B=90°,F为CD的中点,
∴AC= AB2+BC2=62+82=10 ,
∵AO=OC,CF=FD,
∴OF= 12 AD= 12 BC=4,
∵∠AEC=90°,
∴OE= 12 AC= 12×10 =5,
由三角形的三边关系得,O、E、F三点共线时EF最大,
此时EF最大=4+5=9.
故答案为:C.
7.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,AC=12,BD=16,
∴AC⊥BD, OA=OC=12AC=6,OB=OD=12BD=8,
∴∠DOC=90°, CD=OC2+OD2=62+82=10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故答案为:C.
8.解:∵四边形ABCD是矩形,
∴AB=CD=2,∠A=∠D=∠DCB=90°,
∵∠DCE=45°,
∴DE=DC=2,
∴EC=2 2 ,
∵∠DCE=45°,
∴∠DEC=45°,
∵EB平分∠AEC,
∴∠AEB=∠BEC= 12 ∠AEC= 180°-45°2 =67.5°,
∵AD∥BC
∴∠AEB=∠EBC,
∴∠BEC=∠EBC,
∴BC=CE=2 2 ,
∴AD=BC=2 2 ,
∴AE=AD-DE=2 2 -2,
故答案为:B.
9.解:由题意得,△AED和△BCG是等腰直角三角形,
∴ ∠ADE=∠DAE=∠BCG=∠GBC=45°
∵四边形ABCD是平行四边形,
∴AD=BC,CD=AB,∠ADC=∠ABC,∠BAD=∠DCB
∴∠HDC=∠FBA,∠DCH=∠BAF,
∴△AED≌△CGB,△CDH≌ABF
∴AE=DE=BG=CG
∵四边形HEFG是矩形
∴GH=EF,HE=GF
设AE=DE=BG=CG=a, HE=GF= b ,GH=EF= c
过点O作OP⊥EF于点P,OQ⊥GF于点Q,
∴OP//HE,OQ//EF
∵点O是矩形HEFG的对角线交点,即HF和EG的中点,
∴OP,OQ分别是△FHE和△EGF的中位线,
∴ OP=12HE=12b , OQ=12EF=12c
∵ SΔBOF=12BF·OQ=12(a-b)×12c=14(a-b)c
SΔAOE=12AE·OP=12a×12b=14ab ?
∵ SΔBOF=SΔAOE
∴ 14(a-b)c=14ab ,即 ac-bc=ab
而 S1=SΔAED=12AE·DE=12a2 ,
S2=SΔAFB=12AF·BF=12(a+c)(a-b)=12(a2-ab+ac-bc)=12(a2-ab+ab)=12a2 ?
所以, S1=S2 ,A符合题意,
S3=HE·EF=(a-b)(a+c)=a2-bc-ab+ac=a2+ab-ab=a2 ?
∴ S1≠S3 ,B不符合题意,
而 AB=AD 于 EH=GH 都不一定成立,故 C,D 都不符合题意,
故答案为:A
10.解:∵将纸片ABCD沿直线EF折叠,
∴FC=FH,∠HFE=∠CFE,
∵AD∥BC,
∴∠HEF=∠EFC=∠HFE,HE∥FC,
∴△HFE为等腰三角形,
∴HE=HF=FC,
∵EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴EH∥CF,且HE =FC,
∴四边形CFHE是平行四边形,
∵FC=FH,
∴四边形CFHE是菱形,
故①符合题意;
∵HC为菱形的对角线,
∴∠BCH=∠ECH,∠BCD=90°,
∴只有∠DCE=30°时EC平分∠DCH,
故②不符合题意;
过点F作FM⊥AD于M,
点H与点A重合时,BF最小,设BF=x,则AF=FC=8﹣x,
在Rt△ABF中,AB2+BF2=AF2 ,
即42+x2=(8﹣x)2 ,
解得x=3,
点G与点D重合时,点H与点M重合,BF最大,CF=FM=DM=CD=4,
∴BF=4,
∴线段BF的取值范围为3≤BF≤4,
故③符合题意;
当点H与点A重合时,由③中BF=3,
∴AF=AE=CF=EC=8-3=5,
则ME=5﹣3=2,
由勾股定理得,
EF= MF2+ME2=42+22 =2 5 ,
故④符合题意;
综上所述,结论正确的有①③④共3个.
故答案为:C.
二、填空题
11.如下图:
过点N作 GH//AB ,分别交BC于点G , 交AD于点H , 易得 GH//CD , GH=AB=CD ,
∵四边形ABCD是矩形
∴ ∠C=∠D=90? , AB//DC , AB=CD , AD=BC ,
在 Rt△AMD 中,点N是线段AM中点,点M、点N分别在线段CD、GH上,
∴ NH=12MD ,
又∵M是CD的中点,
∴MD=12CD=12AB=1 ,
∴NH=12MD=1×12=12 ,
∴GN=GH-NH=2-12=32 ,
∵ GH//CD , ∠C=90? ,
∴ ∠BGN=90? ,
在 Rt△BGN 中, BG=AH=12BC=32 , GN=32 ,
∴BN=2GN=2×32=322 .
故答案为: 322
12.解:当 ΔCEB' 为直角三角形时,有两种情况:
①当点 B' 落在矩形内部时,如答图1所示.
连结 AC ,
在 RtΔABC 中, AB=3 , BC=4 ,
∴AC=42+32=5 ,
∵∠B 沿 AE 折叠,使点 B 落在点 B' 处,
∴∠AB'E=∠B=90° ,
当 ΔCEB' 为直角三角形时,只能得到 ∠EB'C=90° ,
∴ 点 A 、 B' 、 C 共线,即 ∠B 沿 AE 折叠,使点 B 落在对角线 AC 上的点 B' 处,
∴EB=EB' , AB=AB'=3 ,
∴CB'=5-3=2 ,
设 BE=x ,则 EB'=x , CE=4-x ,
在 RtΔCEB' 中,
∵EB'2+CB'2=CE2 ,
∴x2+22=(4-x)2 ,解得 x=32 ,
∴BE=32 ;
②当点 B' 落在 AD 边上时,如答图2所示.
此时 ABEB' 为正方形,
∴BE=AB=3 .
综上所述, BE 的长为 32 或3.
故答案为: 32 或3.
13.解: ∵ 四边形ABCD是矩形,点G是DF的中点.
∴∠DAF=90°,AG=DG,AD//BC, ?
∴∠GAD=∠GDA, ?
∴ ?∠AGE=∠ADG+∠DAG=2∠DAG ,
∵AD//BC, ?
∴∠ADG=∠DEC, ?
又∵∠AED=2∠CED ,
∴∠AED=∠AGE ,
∴AE=AG ,
∵AG=4,
∴AE=4,
∵四边形ABCD为矩形,
∴∠BAD=∠ABC=90°,
在Rt△AEB中,由勾股定理可求AB= AE2-BE2=42-12 = 15 ,
∴CD= AB= 15 ,
故答案为: 15 .
14.解:∵ ∠BAC=90° ,且 BA=3 , AC=4 ,∴ BC=BA2+AC2=5 ,
∵ DM⊥AB , DN⊥AC ,∴ ∠DMA=∠DNA=∠BAC=90° ,
∴四边形 DMAN 是矩形.
如图,连接AD , 则 MN=AD ,
∴当 AD⊥BC 时, AD 的值最小,此时, ΔABC 的面积 =12AB×AC=12BC×AD ,
∴ AD=AB×ACBC=125 ,∴ MN 的最小值为 125 ;
故答案为 125 .
15.解:∵ EF⊥AC ,点 G 是 AE 中点,
∴ OG=AG=GE=12AE ,
∵ ∠AOG=30° ,
∴ ∠OAG=∠AOG=30° ,
∠GOE=90°-30°=60° ,
∴ △OGE 是等边三角形,故③符合题意;
设 AE=2a ,则 OE=OG=a ,
由勾股定理得, AO=AE2-OE2=(2a)2-a2=3a ,
∵ O 为 AC 中点,
∴ AC=2AO=23a ,
∴ BC=12AC=12×23a=3a ,
在 Rt△ABC 中,由勾股定理得, AB=(23a)2-(3a)2=3a ,
四边形 ABCD 是矩形,
∴ CD=AB=3a ,
∴ DC=3OG ,故①符合题意;
∵ OG=a , BC=3a , 12BC=32a ,
∴ OG≠12BC ,故②不符合题意;
∵ S△AOE=12a?3a=32a2 ,
SABCD=3a?3a=33a2 ,
∴ S△AOE=16SABCD ,故④符合题意;
综上所述,结论符合题意是①③④,
故答案为:①③④.
16.解:∵将 △BCE 沿 BE 折叠得 △BFE ,
∴ BC=BF ,
如图示,过点 N 作 NG⊥BF 交 BF 于点 G ,
∵ AN 是 ∠ABF 的平分线
∴ AN=NG ,
又∵ S△NFB=12BF·NG=12NF·AB , NF=12BC=12×16=8 ,
可得: BF·AN=12BC·AB ,即 AN=12AB ,
设 AB=2x ,则 AN=x , AF=AN+NF=x+8 ,
在 Rt△ABF 中, AB2+AF2=BF2 ,
即: (2x)2+(x+8)2=162 ,
解之得: x=245 ,负值已舍去,
∴ AB=485 ,
故答案为: 485 .
三、解答题
17. (1)证明:∵四边形ABCD为矩形,
∴AB∥CD,AB=CD,CB⊥AE,
又∵AC=EC,
∴AB=BE,
∴BE=CD,BE∥CD,
∴四边形BECD为平行四边形
(2)证明:∵AB=AD,
∴矩形ABCD是正方形,
∵EG⊥AC,
∴∠E=∠GAE=45°,
∴GE=GA,
又∵AF=BE,
∴AB=FE,
∴FE=AD,
在△EGF和△AGD中,
{GE=GA∠E=∠DAC=45?EF=AD ,
∴△EGF≌△AGD(SAS),
∴GF=GD,∠DGA=∠FGE,
∠DGF=∠DGA+∠AGF=∠EGF+∠AGF=∠AGE=90°,
∴△DGF是等腰直角三角形
18.(1)矩形
(2)解:如图1,过点P作PE⊥AO于点E,
∵∠PAO=∠POA,
∴PA=PO,
∵PE⊥AO,
∴AE=EO=4,
∴P(﹣4,6);
(3)解:如图2,在Rt△OCQ和Rt△OC'Q中,
{CO=C'OOQ=OQ ,
∴Rt△OCQ≌Rt△OC'Q(HL),
∴∠OQC=∠OQC',
又∵OP∥C'Q,
∵∠POQ=∠OQC',
∴∠POQ=∠PQO,
∴PO=PQ,
∵BP=QP,
∴BP=OP=x,
在Rt△OPC中,x2=(8﹣x)2+62 ,
解得:x= 254 .
故S△OPQ= 12 ×CO×PQ= 12×6×254=754 .
(1)∵点A的坐标为(﹣8,0),点B(﹣8,6),C(0,6),
?
∴∠COA=∠OAB=∠B=90°,
∴四边形OABC是矩形.
故答案为矩形;
19. (1)证明:∵四边形ABCD是菱形,∴AC上BD,∠AOD=90°∵EA⊥AO,DE⊥DO,∴∠EAO=∠EDO= 90°,∴四边形AODE是矩形.
(2)解:∵四边形AODE是矩形,∴∠DOA =∠EAO= 90°∵∠DAE = 60°,AD
= 6,∴∠DAO=30°,DO= 12 AD=3,∴BD=6
20. (1)解:四边形 CEDG 是菱形,理由如下:
∵四边形 ABCD 为矩形,G是对角线 BD 的中点,
∴ GB=GC=GD ,
∵ CF=GC ,
∴ GB=GC=GD=CF ,
∵四边形 DCFE 是菱形,
∴ CD=CF=DE , DE//CG ,
∴ DE=GC ,
∴四边形 CEDG 是平行四边形,
∵ GD=GC ,
∴四边形 CEDG 是菱形
(2)解:∵ CD=CF , GB=GD=GC=CF ,
∴ △CDG 是等边三角形,
∴ CD=BG , GCD=∠DGC=60° ,
∴ ∠DCF=∠BGC=120° ,
∴ △BGC≌△DCF(SAS) ,
∴ DF=BC=3 .
21. (1)解:由平行四边形的性质可知 AD//BC ,
∴ ∠AB'E=∠CEB' ,
由翻折可知 ∠AB'E=∠ABE ,
∴ ∠CEB'=∠ABE ,
∴ AB//B'E .
∴四边形 ABEB' 是平行四边形.
再由翻折可知 AB'=AB ,
∴四边形 ABEB' 是菱形
(2)解:由翻折可知 ∠BPF=∠QPF ,
∵ AD//BC ,
∴ ∠BPF=∠QFP ,
∴ ∠QPF=∠QFP ,
∴QF=QP,
∴ △PFQ 是等腰三角形
(3)解:如图,延长 PB' 交AD于点G,
根据题意可知 ∠FA'M=∠GB'M=90° ,
在 △FA'M 和 △GB'M 中, {∠FA'M=∠GB'M=90°A'M=B'M∠FMA'=∠GMB' ,
∴ △FA'M?△GB'M(ASA) ,
∴ A'F=B'G=AF=2 , FM=GM .
根据(2)同理可知 △PFG 为等腰三角形.
∴FG=PG.
∵ A'F=AM=2 ,
∴在 Rt△A'FM 中, FM=A'M2+A'F2=22 ,
∴ FG=2FM=42 ,
∴ PG=42 ,
∴ PB=PB'=PG-B'G=42-2 .
22. (1)解:如图1中,
∵ OA=9 , OC=15 ,
∵ △DEC 是由 △OEC 翻折得到,
∴ CD=OC=15 ,
在 Rt△DBC 中, DB=DC2-BC2=12 ,
∴ AD=3 ,设 OE=ED=x ,
在 Rt△DBC 中, x2=(9-x)2+32 ,
解得 X=5 ,
∴ E(0,5) ,
设直线 EC 的解析式为 y=kx+5 ,把 (15,0) 代入得到 k=-13 ,
∴直线 EC 的解析式为 y=-13x+5
(2)解:①证明:如图2中,
∵ MD'=MO , ∠D'MN=∠OMN ,
∵ OM//GD' ,
∴ ∠OMT=∠D'TM ,
∴ ∠D'MT=∠D'TM ,
∴ D'M=D'T ,
∴ OM=DT ,
∵ OA=DG ,
∴ AM=TG .
②如图3中,连接 OT ,
由(2)可得 OT=D'T ,
由勾股定理可得 x2+y2=(9-y)2 ,
得 y=-118x2+92 .
结合(1)可得 AD'=OG=3 时, x 最小,从而 x≥3 ,
当 MN 恰好平分 ∠OAB 时, AD' 最大即 x 最大,
此时 G 点与 N 点重合,四边形 AOND' 为正方形,
故 x 最大为9.从而 x≤9 ,
∴ 3≤x≤9
(3)解:如图4中, x=6 时, y=52 ,即点 T 坐标 (6,52) .
∴ OM=D'T=9-52=132 ,
①当 MD' 为对角线时,点 P 与 T 重合, QM=D'T=132 ,
∴ OQ=13 ,
∴此时点 Q 坐标 (0,13) .
② D'M 为边时,∵四边形 MD'QP 是平行四边形,
又∵四边形 D'MOT 是平行四边形,
∴点 P 与 T 重合,点 Q 与点 O 重合,
∴点 Q 坐标 (0,0) ,
③当点 P″ 在第四象限点时,四边形 MD'Q″P″ 是平行四边形时,
∵直线 NM 的解析式为 y=-23x+132 ,
∵ D'Q″//MN ,
∴直线 D'Q″ 的解析式为 y=-23x+13 ,
当 y=0 时, x=392 ,Q″(392,0)
综上所述,以 M 、 F 、 Q 、 P 为顶点的四边形是平行四边形时,点 Q 坐标 (0,0) 或 (0,13) 或 (392,0)
23.(1)解: D(2b-2,1) ; E(2b,0)
(2)解: CB 与 O1A1 的交点为M, C1B1 与 OA 的交点为N,如图:
∵ 四边形 OABC ,四边形 O1A1B1C1 是矩形,
∴CB//OA , C1B1//O1A1 ,
∴ 四边形 DMEN 是平行四边形,
∵ 矩形 OABC 关于直线 DE 的对称图形为矩形 O1A1B1C1 ,
∴∠1=∠2 ,
∵CB//OA ,
∴∠2=∠3 ,
∴∠1=∠3 ,
∴DM=ME ,
∴ 平行四边形 DMEN 是菱形,
过点D作 DH⊥OA 于点H,
由 D(2b-2,1) , E(2b,0) ,
可知 CD=2b-2 , OE=2b , OH=CD=2b-2 ,
∴EH=OE-OH=2b-(2b-2)=2 ,
设菱形 DMEN 的边长为 m ,
在 Rt△DHN 中, DH=1 , HN=EH-NE=2-m , DN=m ,
由 DH2+HN2=DN2 ,得 12+(2-m)2=m2 ,
解得: m=54 ,
∴ S菱形DMEN=NE?DH=54×1=54 ,
所以重叠部分菱形 DMEN 的面积不变, 为 54 ;
(3)S最大=53 ; S最小=1
解:(1) ∵ 四边形 OABC 是矩形,
?
∴CB//x 轴,
由点A,C的坐标分别为 (3,0) , (0,1) .
可得点D的纵坐标为 1 ,
当 y=1 时, y=-12x+b ,
解得: x=2b-2 ,
∴D 的坐标为 (2b-2,1)
当 y=0 时, y=-12x+b ,
解得: x=2b ,
∴E 的坐标为 (2b,0)
(3) 如下图所示,
当这个菱形 DNEM 是正方形时,即 NE=1 时,菱形的面积最小,最小值是1;
如下图所示,
当这个菱形A与E重合时,菱形 CNAM 的面积最大,
设 CN=AN=x ,则 ON=AO-AN=3-x ,
Rt△CON 中, 12+(3-x)2=x2
解之得: x=53 ,
∴ AN=53
∴菱形面积的最大值是 AN·CO=1×53=53 .
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
