1.3正方形的性质与判定 新思维同步提高训练(Word版含解答)-2021-2022学年九年级数学北师大版上册
文档属性
| 名称 | 1.3正方形的性质与判定 新思维同步提高训练(Word版含解答)-2021-2022学年九年级数学北师大版上册 |  | |
| 格式 | docx | ||
| 文件大小 | 490.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-28 13:36:36 | ||
图片预览


文档简介
1.3正方形的性质与判定 新思维同步提高训练(Word版含解答)-2021-2022学年九年级数学北师大版上册
一、选择题
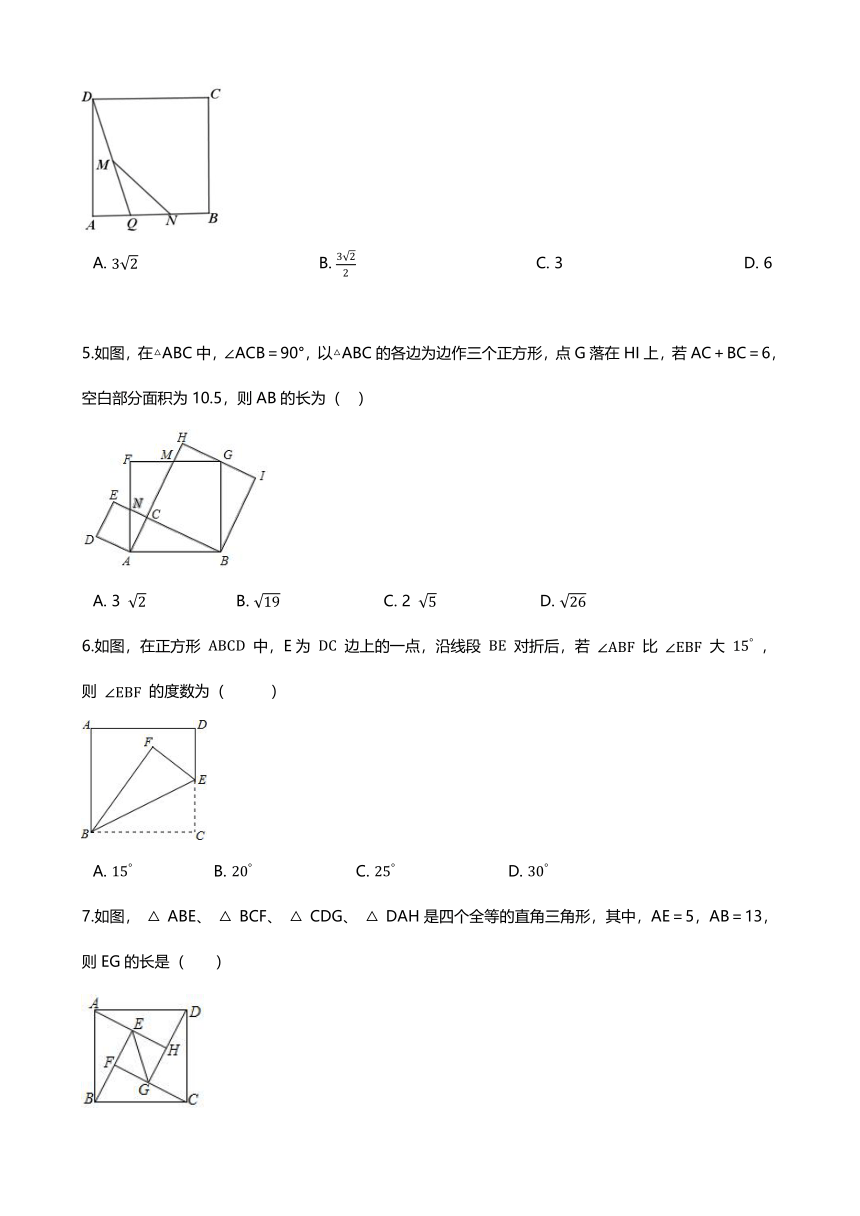
1.如图,将正方形 OEFG 放在平面直角坐标系中,O是坐标原点,点 E(2,3) ,则点F的坐标为(??? )
A.?(-1,5)??????????????B.?(-2,3)????????????????C.?(5,-1)????????????????D.?(-3,2)
2.如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为(? )
A.?1?????????????B.?2?????????????????C.?3???????????????D.?2
3.如图,在边长为2的正方形ABCD中,连接对角线AC,将△ADC沿射线CA的方向平移得到△A′D′C′,分别连接BC′,AD′,BD′,则BC′+BD′的最小值为(?? )
A.?22????????????????B.?4????????????C.?42????????????????????D.?25
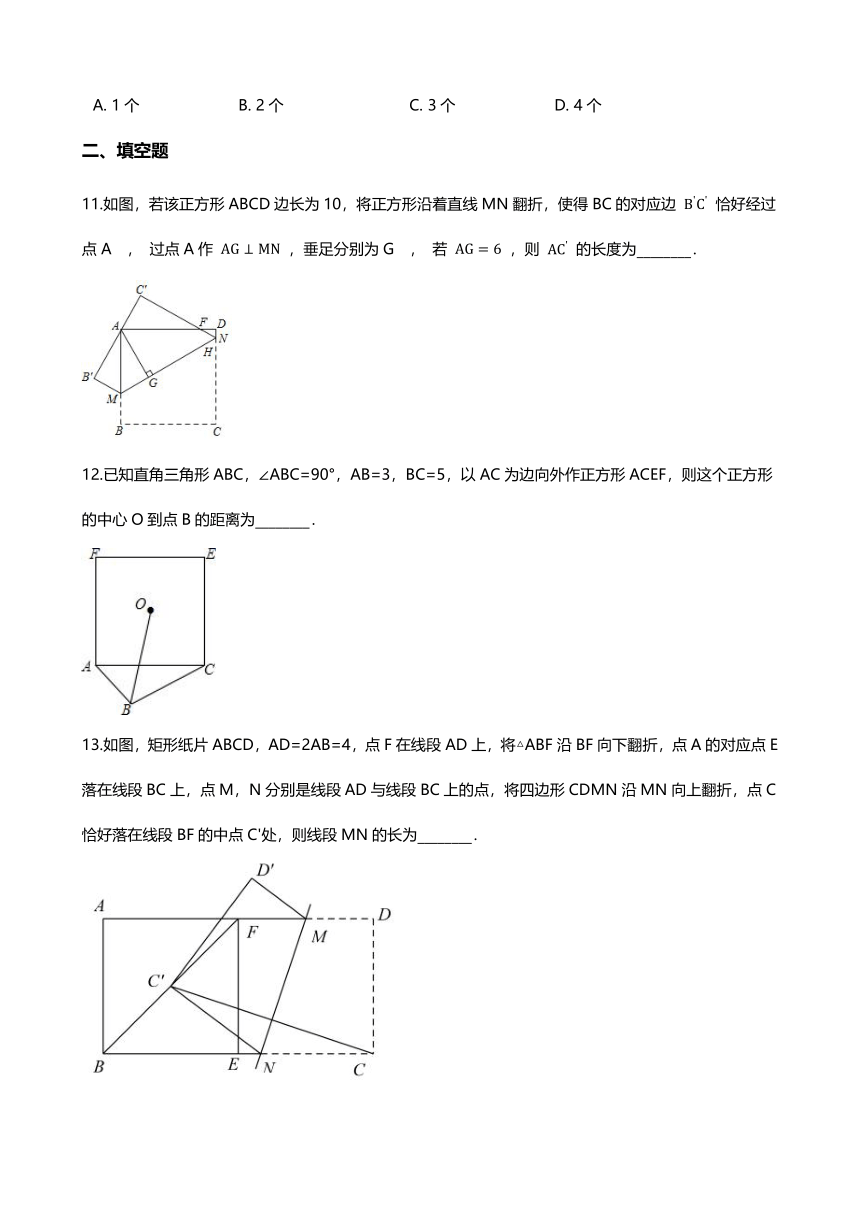
4.如图,在正方形ABCD中,AB=6,点Q是AB边上的一个动点(点Q不与点B重合),点M,N分别是DQ,BQ的中点,则线段MN=(?? )
A.?32????????????????????????????????????????B.?322????????????????????????????????????????C.?3????????????????????????????????????????D.?6
5.如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为10.5,则AB的长为(?? )
A.?3 2????????????????????B.?19???????????????????????C.?2 5???????????????????????D.?26
6.如图,在正方形 ABCD 中,E为 DC 边上的一点,沿线段 BE 对折后,若 ∠ABF 比 ∠EBF 大 15° ,则 ∠EBF 的度数为( )
A.?15°??????????????????B.?20°???????????????????????C.?25°?????????????????????????D.?30°
7.如图, △ ABE、 △ BCF、 △ CDG、 △ DAH是四个全等的直角三角形,其中,AE=5,AB=13,则EG的长是( )
A.?7 2??????????????????B.?6 2????????????????????????C.?7????????????????????????D.?7 3
8.如图,在 △ABC 中, ∠ACB=90° ,以 △ABC 的各边为边分别作正方形 BAHI ,正方形 BCFG 与正方形 CADE .延长 BG , FG 分别交 AD , DE 于点K,J,连结 DH , IJ .图中两块阴影部分面积分别记为 S1 , S2 ,若 S1:S2=1:4 ,四边形 SBAHE=18 ,则四边形 MBNJ 的面积为(?? )
A.?5????????????????????????????????B.?6??????????????????????C.?8??????????????????????????D.?9
9.由四个全等的直角三角形和一个小正方形组成的大正方形 ABCD 如图所示.过点 D 作 DF 的垂线交小正方形对角线 EF 的延长线于点 G ,连结 CG ,延长 BE 交 CG 于点 H .若 AE=2BE ,则 CGBH 的值为(?? )
A.?32???????????????????????????B.?2??????????????????????C.?3107???????????????????????D.?355
10.如图,正方形 ABCD 中,在 AD 的延长线上取点 E , F ,使 DE=AD , DF=BD ,连接 BF 分别交 CD , CE 于 H , G ,下列结论:① HF=2HG ;② ∠GDH=∠GHD ;③图中有8个等腰三角形;④ S△CDG=S△DNF .其中正确的结论个数是(?? )
A.?1个??????????????????????B.?2个????????????????????????????C.?3个??????????????????????D.?4个
二、填空题
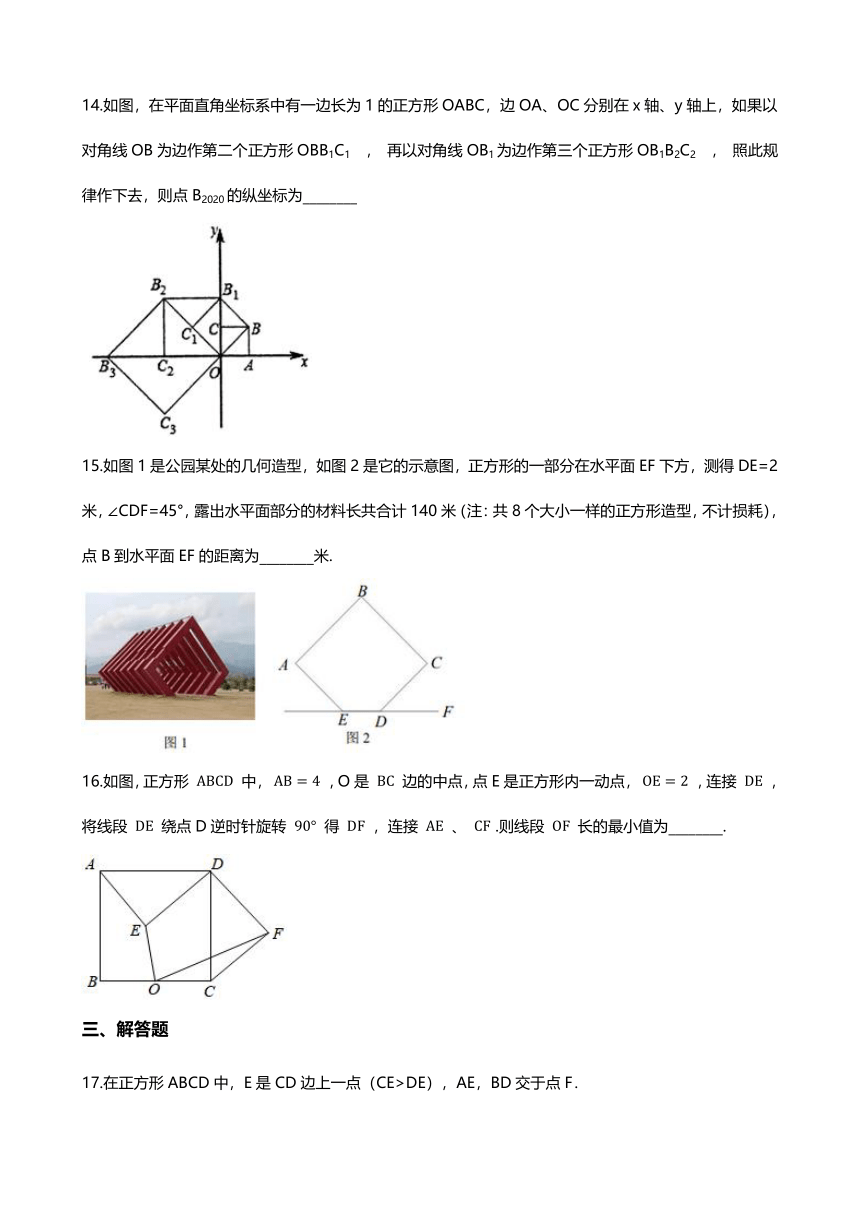
11.如图,若该正方形ABCD边长为10,将正方形沿着直线MN翻折,使得BC的对应边 B'C' 恰好经过点A , 过点A作 AG⊥MN ,垂足分别为G , 若 AG=6 ,则 AC' 的长度为________.
12.已知直角三角形ABC,∠ABC=90°,AB=3,BC=5,以AC为边向外作正方形ACEF,则这个正方形的中心O到点B的距离为________.
13.如图,矩形纸片ABCD,AD=2AB=4,点F在线段AD上,将△ABF沿BF向下翻折,点A的对应点E落在线段BC上,点M,N分别是线段AD与线段BC上的点,将四边形CDMN沿MN向上翻折,点C恰好落在线段BF的中点C'处,则线段MN的长为________.
14.如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1 , 再以对角线OB1为边作第三个正方形OB1B2C2 , 照此规律作下去,则点B2020的纵坐标为________
15.如图1是公园某处的几何造型,如图2是它的示意图,正方形的一部分在水平面EF下方,测得DE=2米,∠CDF=45°,露出水平面部分的材料长共合计140米(注:共8个大小一样的正方形造型,不计损耗),点B到水平面EF的距离为________米.
16.如图,正方形 ABCD 中, AB=4 ,O是 BC 边的中点,点E是正方形内一动点, OE=2 ,连接 DE ,将线段 DE 绕点D逆时针旋转 90° 得 DF ,连接 AE 、 CF .则线段 OF 长的最小值为________.
三、解答题
17.在正方形ABCD中,E是CD边上一点(CE>DE),AE,BD交于点F.
(1)如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.
求证:∠EAB=∠GHC;
(2)AE的垂直平分线分别与AD,AE,BD交于点P,M,N,连接CN.
①依题意补全图形;
图1????????????????? 备用图
②用等式表示线段AE与CN之间的数量关系,并证明.
18.问题情境:
(1)如图1,已知正方形ABCD,点E在CD的延长线上,以CE为边构造正方形CEFG,连接BE和DG,则BE和DG的关系为________。
(2)继续探究:如图2,若正方形ABCD的边长为3,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE。
①求证:DG⊥BE。
②连接BG,若AE=1,求BG长。
19.如图,点 P 为正方形 ABCD 对角线 BD 上一点, PE⊥BC 于点 E , PF⊥CD 于点 F .
(1)求证: PA=EF .
(2)若正方形 ABCD 的边长为12,求,四边形 PFCE 的周长.
20.如图
(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为________.
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);
②图3中补全图形,直接写出∠EOF的度数.
21.如图①,四边形ABCD是正方形,E是对角线BD上一点,连接AE、CE
(1)求证:AE=CE;
(2)如图②,点P是边CD上的一点,且PE⊥BD于E,连接BP,点O为BP的中点,连接OE。若∠PBC=30°,求∠POE的度数;
(3)在(2)的条件下,若OE= 2 ,求CE的长。
22.如图,已知四边形ABCD是正方形.
(1)如图1,若E、F、G分别是AB、BC、CD边上的点,AF和EG交于点O.现在提供三个关系:①AF⊥EG;②AO=FO;③AF=EG.从三个关系中选择一个作为条件,一个作为结论,形成一个真命题,完成下列填空并证明:你选择的条件是________,结论是________.(只要填写序号).
(2)如图2,点E、F分别在AD、AB上,BE⊥CF,垂足为点O,连接EF、EC,M、N分别是BF、CE的中点,MN分别交BE、CF于点G、H,求证:OG=OH;
(3)如图3,AB=3cm,E为CD边上一点,∠DAE=30°,O为AE的中点,过点O的直线分别交AD、BC于点M、N,若MN=AE,请直接写出AM的长.
23.综合与实践﹣﹣图形变换中的数学问题.
问题情境:
如图1,在Rt△ABC中,AB=5,∠ABC=90°,∠BAC=45°.将△ABC沿AC翻折得到△ADC , 然后展平,两个三角形拼成四边形ABCD .
(1)求证:四边形ABCD是正方形.
(2)初步探究:
将△ABC从图1位置开始绕点B按逆时针方向旋转角度α(0°<α<90°),得到△EBF , 其中点A , C的对应点分别是点E , F , 连接AE , FC并分别延长,交于点M . 试猜想线段AM与FM的数量关系和位置关系,并说明理由.
(3)如图3,连接DE , 当DE∥CM时,请直接写出CM的长.
答案
一、选择题
1.解:如图所示,过点E作EA⊥x轴,垂足为A , 过点F作FB⊥EA , 交AE的延长线于点B , 交y轴与点C ,
∵四边形OEFG是正方形,
∴FE=EO , ∠FEO=90°,
∴∠FEB+∠AEO=90°,∠AEO+∠AOE=90°,
∴∠FEB =∠EOA ,
∴△FEB≌△EOA ,
∴FB=EA , EB=OA ,
∵E(2,3),
∴FB=EA=3,EB=OA=2,
∵EA⊥x轴,FB⊥EA , OC⊥x轴,
∴四边形OABC是矩形,
∴BC=OA=2,
∴FC=FB-BC=1,BA=EB+EA=5,
∵点F在第二象限,
∴点F(-1,5)
故答案为:A .
2.解:∵四边形ABCD是正方形,
∴AB∥CD,∠A=90°,
∴∠EFD=∠BEF=60°,
∵将四边形EBCF沿EF折叠,点B恰好落在AD边上,
∴∠BEF=∠FEB'=60°,BE=B'E,
∴∠AEB'=180°﹣∠BEF﹣∠FEB'=60°,
∴B'E=2AE,
设BE=x,则B'E=x,AE=3﹣x,
∴2(3﹣x)=x,
解得x=2.
故答案为:D.
3.解:连接DD′,当等腰Rt△ADC在射线CA上运动时,点D运动轨迹为直线DD',
∵AB∥C′D′,且AB=C′D′,
∴四边形ABC′D′为平行四边形,
∴BD′+BC′=D′B+D′A,
将点B关于直线l对称到点B′,BD′+BC′=D′B+D′A= D′B′+D′A≥AB′,当D′、B′、A三点共线时,BC′+BD′的最小,最小值为AB′长,
作A′′B′⊥AD交AD延长线于点A′′,
由对称可知,BD′=BD,∠ADB=∠AD B′,∠BAD=∠B′A′′D,
∴△BAD≌△B′A′′D,
∴A′′D=AD=2,A′′B′=AB=2,
AB′= AA''2+B'A''2= 25 ,
?故答案为:D.
4.解:连接 BD ,如图,
∵四边形ABCD是正方形,
∴AB=AD=6,
∴ BD=AB2+AD2=62 ,
当点Q在AB边上运动时(点Q不与点B重合),MN一直是△BQD的中位线,
则线段 MN=12BD=32 .
故答案为:A.
5.解:∵四边形ABGF是正方形,
∴∠FAB=∠AFG=∠ACB=90°,
∴∠FAC+∠BAC=∠FAC+∠ABC=90°,
∴∠FAC=∠ABC,
在△FAM与△ABN中,
{∠F=∠NAB=90°∠FAM=∠ABNAF=AB ,
∴△FAM≌△ABN(AAS),
∴S△FAM=S△ABN ,
∴S△ABC=S四边形FNCM ,
∵在△ABC中,∠ACB=90°,
∴AC2+BC2=AB2 ,
∵AC+BC=6,
∴(AC+BC)2=AC2+BC2+2AC?BC=36,
∴AB2+2AC?BC=36,
∵AB2﹣2S△ABC=10.5,
∴AB2﹣AC?BC=10.5,
∴3AB2=57,
解得AB= 19 或﹣ 19 (负值舍去).
故答案为:B.
6.解:∵∠FBE是∠CBE折叠形成,
∴∠FBE=∠CBE,
∵∠ABF-∠EBF=15°,∠ABF+∠EBF+∠CBE=90°,
∴∠EBF=25°,
故答案为:C.
7.解:在Rt△ABE中,AE=5,AB=13,
由勾股定理得,BE= AB2-AE2 = 132-52 =12,
∵△ABE、△BCF、△CDG、△DAH是四个全等的直角三角形,
∴∠AEB=∠BFC=∠CGD=90°,BF=CG=DH=AE=5,
∴∠FEB=∠EFC=∠FGD=90°,EF=EH=12﹣5=7,
∴四边形EFGH为正方形,
∴EG= 72+72 =7 2 ,
故答案为:A.
8.解:∵ S1:S2=1:4
∴ GJBC=12
∵四边形 BCFG 与四边形 CADE 是正方形
∴ BC=FC=FG=GB=2GJ
∴ AC=AD=DE=CE=BC+GJ=3GJ
∵ ∠ACB=90°
∴ AB=AC2+BC2=13GJ
∵ AH=AB , ∠ADH=180°-∠ADE=90°
∴ HD=AH2-AD2=2GJ
∵四边形 SBAHE=S△AHD +梯形 SADEB=18
∴ 12AD×HD+12(AD+BE)×DE=12×3GJ×2GJ+12(3GJ+GJ)×3GJ=18
∴ GJ=2
∴ AF=AC-FC=3GJ-2GJ=GJ=BE
∵ ∠CAB+∠ABC=90° , ∠ABC+∠EBM=180°-∠ABI=90°
∴ ∠CAB=∠EBM ,即 ∠FAN=∠EBM
∵四边形 BCFG 与四边形 CADE 是正方形
∴ ∠AFN=180°-∠CFN=90° , ∠BEM=90°
∴ {∠AFN=∠BEM=90°AF=BE∠FAN=∠EBM
∴ △FAN≌△EBM
∴ S△FAN=S△EBM
∴ S△ABC= 四边形 SCFNB+S△EBM
∵ ∠FCE=∠CEJ=∠EJF=∠JFC=90°
∴四边形 CFJE 是矩形
∴矩形 SCFJE= 四边形 SMBNJ+ 四边形 SCFNB+S△EBM= 四边形 SMBNJ+S△ABC
∴四边形 SMBNJ = 矩形 SCFJE- S△ABC =JE×CE-12AC×BC=2GJ×3GJ-12×3GJ×2GJ=6
故答案为:B.
9.如图,设BH交CF于P,CG交DF于Q,
∵由四个全等的直角三角形和一个小正方形组成的大正方形 ABCD ,
∴BE=PC=DF,AE=BP=CF,
∵ AE=2BE ,
∴BE=PE=PC=PF=DF,
∵∠CFD=∠BPC,
∴DF//EH,
∴PH为△CFQ的中位线,
∴PH= 12 QF,CH=HQ,
∵四边形EPFN是正方形,
∴∠EFN=45°,
∵GD⊥DF,
∴△FDG是等腰直角三角形,
∴DG=FD=PC,
∵∠GDQ=∠CPH=90°,
∴DG//CF,
∴∠DGQ=∠PCH,
在△DGQ和△PCH中, {∠GDQ=∠CPHDG=PC∠DGQ=∠PCH ,
∴△DGQ≌△PCH,
∴PH=DQ,CH=GQ,
∴PH= 13 DF= 13 BE,CG=3CH,
∴BH=BE+PE+PH= 73BE ,
在Rt△PCH中,CH= PC2+PH2=BE2+(13BE)2 = 103BE ,
∴CG= 10 BE,
∴ CGBH=10BE73BE=3107 .
故答案为:C.
10.解:∵DF=BD ,
∴∠DFB=∠DBF
∵四边形ABCD是正方形,
∵AD//BC , AD=BC=CD , ∠ADB=∠DBC=45°,
∴DE//BC , ∠DFB=∠GBC ,
∵DE=AD ,
∴DE=BC ,
∴四边形DBCE是平行四边形,
∴∠DEC=∠DBC=45°,
∴∠DEC=∠ADB=∠DFB+∠DBF=2∠EFB=45°,
∴∠GBC=∠EFB=22.5°,∠CGB=∠EGF=22.5°=∠GBC ,
∴CG=BC=DE ,
∵BC=CD ,
∴DE=CD=CG ,
∴∠DEG=∠DCE=45°,EC= 2 CD , ∠CDG=∠CGD= 12 (180°-45°)=67.5°,
∴∠DGE=180°-67.5°=112.5°,
∵∠GHC=∠CDF+∠DFB=90°+22.5°=112.5°,
∴∠GHC=∠DGE ,
∴△CHG≌△EGD(AAS),
∴∠EDG=∠CGB=∠CBF ,
∴∠GDH=90°-∠EDG , ∠GHD=∠BHC=90°-∠CGB ,
∴∠GDH=∠GHD ,
∴∠GDH=∠GHD , 故②符合题意;
∵∠EFB=22.5°,
∴∠DHG=∠GDH=67.5°,
∴∠GDF=90°-∠GDH=22.5°=∠EFB ,
∴DG=GF ,
∴HG=DG=GF ,
∴HF=2HG , 即EC≠HF=2HG , 故①符合题意;
∵△CHG≌△EGD ,
∴S△CHG=S△EGD ,
∴ SΔCHG+SΔDHG=SΔEGD+sΔDHG ,即 SΔCDG=SΔCDG≠SΔDHF ,故④不符合题意;
结合前面条件易知等腰三角形有:△ABD、△CDB、△BDF、△CDE、△BCG、△DGH、△EGF、△CDG、△DGF共9个,故③不符合题意;
则正确的个数有2个.
故答案为:B .
二、填空题
11.延长AG交BC于点E ,
则 EG=AG=6 ,
∴AE=12 .
∵正方形ABCD边长为10,
AB=BC=10 .
在 Rt△ABE 中, BE=AE2-AB2=122-102=211 ,
∴CE=BC-BE=10-211 ,
由折叠的性质得, AC'=CE=10-211 ,
故答案为: 10-211 .
12.如图,延长BA到D,使AD=BC,连接OD,OA,OC,
∵四边形ACEF是正方形,∴∠AOC=90°,CO=AO,
∵∠ABC=90°,∠ABC+∠AOC=180°,
∴∠BCO+∠BAO=180°,∠BCO=∠DAO,
在△BCO与△DAO中, {BC=AD∠BCO=∠DAOCO=AO
∴△BCO≌△DAO(SAS),
∴OB=OD,∠BOC=∠DOA,∴∠BOD=∠COA=90°,
∴△BOD是等腰直角三角形,∴BD= 2OB ,
∵BD=AB+AD=AB+BC=8,∴OB= 42 .
故答案为 42 .
13.解:作C'G⊥BC,连接C'C交MN于点K,连接CM
根据题意可得,四边形ABEF为正方形,△BGE为等腰三角形
∴C'G=12×2=1,CG=4-BG=4-1=3
设CN=C'N=x,则GN=3-x
在直角三角形C'GN中,1+(3-x)2=x2 , 解得x=53
∴CN=53
在直角三角形CC'G中,CC'=32+12=10
由折叠可得,CK=CC'2=102 , CK⊥MN
∵12MN×ck=12CN×CD
∴MN=CN×CDCK=2103
14.解: ∵正方形OABC边长为1,
∴OB=2 ,
∵正方形OBB1C1是正方形OABC的对角线OB为边,
∴OB1=2,
∴B1点坐标为(0,2),
同理可知OB2=22 ,
∴B2点坐标为(-2,2),
同理可知OB3=4,B3点坐标为(-4,0),
B4点坐标为(-4,-4),B5点坐标为(0,-8),
B6(8,-8),B7(16,0)
B8(16,16),B9(0,32),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的2倍,
∵2020÷8=252…4,
∴B2020的纵横坐标符号与点B4的相同,纵坐标为负数,横坐标是正数,
∴ 点B2020的纵坐标为 -21010.
15.解:如图,延长AE、CD交于一点G,连接BG交EF于H,
∴∠EGD=90°,
∵DE=2,∠CDF=45°,
∴GD=EG=2 ,
设正方形的边长为a,则AE=CD=a-2 ,
∴2AE+2AB=4a-22=1408 ,
解得a=35+428 ,
∴BG=2a=352+88 ,
∴BH=BG-HG=352+88-1=3528 ,
故答案为:3528.
16.如图,连接DO,将线段DO绕点D逆时针旋转90°得DM,连接OF,FM,OM,
∵ ∠EDF= ∠ODM=90°,
∴ ∠EDO=∠FDM,
在△EDO与△FDM中, {DE=DF∠EDO=∠FDMDO=DM
∴ △EDO≌△FDM (SAS) ,
∴ FM=OE=2,
∵正方形ABCD中,
AB=4,O是BC边的中点,
∴ OC=2,
∴ OD=42+22=25
∴ OM=(25)2+(25)2=210
∵OF+MF ≥ OM,
∴ OF≥210-2
∴线段OF长的最小值为 210-2
故答案为: 210-2
三、解答题
17.(1)证明:在正方形ABCD中,AD∥BC,∠BAD=90°,
∴∠AGH=∠GHC.
∵GH⊥AE,
∴∠EAB=∠AGH.
∴∠EAB=∠GHC.
(2)①补全图形,如图所示.
② AE=2CN .
证明:连接AN,连接EN并延长,交AB边于点Q.
∵四边形ABCD是正方形,
∴点A,点C关于BD对称.
∴NA=NC,∠1=∠2.
∵PN垂直平分AE,
∴NA=NE.
∴NC=NE.
∴∠3=∠4.
在正方形ABCD中,BA∥CE,∠BCD=90°,
∴∠AQE=∠4.
∴∠1+∠AQE=∠2+∠3=90°.
∴∠ANE=∠ANQ=90°.
在Rt△ANE中,
∴ AE=2CN .
18.(1)BE= DG,BE⊥DG
(2)①如图2,延长BE, GD交于点H,
∵四边形ABCD是正方形,四边形CEFG是正方形,
∴BC=CD,∠BCD=∠ECG=90°,CE= CG,
∴∠BCE=∠DCG,
∴△BCE≌△DCG(SAS),
∴∠BEC=∠DGC,
∵∠BEC+∠HEC= 180°,
∴∠DGC+∠HEC=180°,
∵∠DGC+∠HEC+ CECG+∠DHE = 360°,
∴∠DHE=90°,
∴DG⊥BE;
②如图3,过点G作GN⊥BC,交BC延长线于点N,
∵AE= 1,AD=3,
∴DE= 2,
∵∠ECG=∠DCN= 90°,
∴∠ECD=∠GCN
又∵EC=CG,∠EDC=∠N=90°,
∴△ECD≌△GCN(AAS),
∴DE=GN=2,CN=CD=3,
∴BN= BC+ CN= 6,
∴BG= BN2+CN2 = 62+22 = 210
解:(1)如图1,延长GD交BE于点H,
∵四边形ABCD是正方形,四边形CEFG是正方形,
∴BC=CD,∠BCD=∠ECG=90°,CE=CG,
∴△BCE≌△DCG(SAS),
∴BE=DG,∠BEC=∠DGC,
∵∠BEC+∠EBC=90°,
∴∠DGC+∠EBC=90°,
∴∠BHG=90°,
∴BE⊥DG;
19.(1)证明:连接PC,
∵四边形ABCD是正方形,
∴AB=CB,∠ABD=∠CBD=45°,∠BCD=90°,
在△ABP与△CBP中,
{AB=CB∠ABD=∠CBDPB=PB ,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PE⊥CD,PF⊥BC,
∴∠PFC=90°,∠PEC=90°.
又∵∠BCD=90°,
∴四边形PFCE是矩形,
∴EF=PC,
∴PA=EF;
(2)解:由(1)知四边形PFCE是矩形,
∴PE=CF,PF=CE,
又∵∠CBD=45°,∠PEB=90°,
∴BE=PE,
又∵BC=12,
∴矩形PFCE的周长为2(PE+EC)=2(BE+EC)=2BC=24.
20.(1)3
(2)解:①如图2,在AD上截取AH=DE,连接EH,作EH的垂直平分线,交DH于F,连接EF,则△EDF就是所求作的三角形.
②如图3,连接OD、OA、OH,
∵O为正方形的中心,
∴OA=OD,∠DOA=90°,
在△AHO和△DEO中,
{AO=OD∠1=∠2AH=DE ,
∴△AHO≌△DEO(SAS),
∴OE=OH,∠4=∠3,
∴∠EOH=∠DOA=90°,
∵OF是EH的垂直平分线,
∴EF=FH,
在△EOF和△HOF中,
{OE=OHOF=OFEF=FH ,
∴△EFO≌△HOF(SSS),
∴∠EOF=∠HOF,
∵∠EOH=∠DOA=90°.
∴∠EOF=45°
解:(1)∵AB的垂直平分线交AC于点D,
∴BD=AD,
∴△BCD的周长=BC+CD+BD=BC+AC=1+2=3,
故答案为:3;
21.(1)证明:∵ 四边形ABCD是正方形 ,
∴AB=BC,∠ABE=∠CBE,BE=BE
∴△ABE≌△CBE(SAS)
∴AE=CE
(2)解:
∵ 四边形ABCD是正方形 ,
∴∠EBC=∠EDP=45°
∵ ∠PBC=30°,
∴∠EBP=15°
∵ PE⊥BD,点O为BP的中点,
∴OE=OB=OP
∴∠OEB=∠EBP=15°
∴∠POE=∠OEB+∠EBP=30°
(3)连接OC,
∵点O为BP的中点,∠BCP=90°
∴OB=OC
∴∠OBC=∠OCB=30°
∴∠POC=∠OBC+∠OCB=60°
∴∠EOC=∠POE+∠POC=90°,
∵OE=OB=OC=2
∴CE=OC2+OE2=2
22. (1)①;③
(2)证明:取EF中点Q,连接QN,QM,
∴ QN//FC,QN=12FC,MQ//BE,MQ=12BE,
由(1)知当BE⊥CF时BE=CF,
∴NQ=MQ,∠QNM=∠QMN,
∵∠QMN=∠OGH,∠QNM=∠OHG,
∴∠OGH =∠OHG,
∴OG=OH;
(3)解:AM=2,
过M作MK⊥BC,
由(1)同理可证△MNK ? △AED,
∴AE⊥MN,∠AOM=90°,
∵AB=3,∠DAE=30°,
∴AD=3,
设DE=x,AE=2x,
则根据勾股定理可得: AE=23 , DE=3 ,
∵O为AE中点,
∴ AO=12AE=3 ,
同理可得:AM=2.
(1)①;③
?证明:过点G作GH⊥AB于H,
由题意知GH=AD=AB,∠GHE=∠B=90°,有∠BAF+∠AFB=90°,
∵AF⊥GE,
∴∠AOE=90°,
∴∠BAF+∠AEG=90°,
∴∠AFB=∠AEG,
∴△AFB ? △GEH(ASA),
∴AF=EG;
23.(1)解:
∵∠ABC=90°,∠BAC=45°,
∴∠BCA=90°﹣45°=45°,
∴∠BAC=∠BCA,
∴AB=BC,
∴△ABC是等腰三角形,
∵△ABC沿AC翻折得到△ADC,
∴△ABC≌△ADC,
∴AD=AB,CD=BC,
∴AB=AD=CD=BC,
∴四边形ABCD是菱形,
∵∠B=90°,
∴四边形ABCD是正方形.
?(2)解:
由旋转可知,△ABC≌△EBF,
∴AB=BE,BC=BF,AC=EF,∠ABE=∠CBF=α,
在△ABE和△CBF中, {AB=BC∠ABE=∠CBFBE=BF ,
∴△ABE≌△CBF(SAS),
∴∠AEB=∠BFC,AE=CF,
∵AB=BC,
∴AB=BE=BC=BF,
∴∠BCF=∠BFC,
∴∠AEB=∠BCF,
∵∠BEF=∠ACB=45°,∠AEB=∠BCF,
∴180°﹣(∠AEB+∠BEF)=180°﹣(∠BCF+∠ACB),
∴∠FEM=∠ACM,
在△ACM和△FEM中, {∠FEM=∠ACM∠M=∠MAC=FE ,
∴△ACM≌△FEM(AAS),
∴AM=FM,∠MAC=∠MFE,
∵∠DAC=∠DCA=45°,
∴∠MAC=45°﹣∠DAM,∠MCA=45°+∠MCD,
∴∠DAM=∠MCD,
∴∠MAC+∠ACM=45°﹣∠DAM+45°+∠MCD=90°,
∴∠M=90°,
∴AM⊥FM,
故答案为:AM⊥FM且AM=FM.
深入探究:
(3)CM= 5
解:(3)取AC的中点G , 连接EG , BG ,
?
∵DE∥CM ,
∴∠DEM=∠M=90°,
∵AG=GE= 52 ,AB=BE ,
在△BAG和△BEG中, {BG=BGAB=BEAG=EG ,
∴△BAG≌△BEG(SSS),
∠BEG=∠BAG=90°,∠GBA+∠GBE= α2 ,
∵∠EBA=α ,
∴∠EAB= 180°-α2 ,
∴∠ABG+∠BAE= α2 + 180°-α2 =90°,
∴BG⊥AE ,
∵AB=5,AG= 52 ,
∴BG= 552 ,
∴ 12 AE? 552 = 12 ×2×5× 52 ,
解得:AE=2 5 ,
设CM=ME=x ,
在Rt△ACM中,x2+(x+2 5 )2=(5 2 )2 ,
∵x>0,
∴x= 5 ,
故CM= 5 .
一、选择题
1.如图,将正方形 OEFG 放在平面直角坐标系中,O是坐标原点,点 E(2,3) ,则点F的坐标为(??? )
A.?(-1,5)??????????????B.?(-2,3)????????????????C.?(5,-1)????????????????D.?(-3,2)
2.如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为(? )
A.?1?????????????B.?2?????????????????C.?3???????????????D.?2
3.如图,在边长为2的正方形ABCD中,连接对角线AC,将△ADC沿射线CA的方向平移得到△A′D′C′,分别连接BC′,AD′,BD′,则BC′+BD′的最小值为(?? )
A.?22????????????????B.?4????????????C.?42????????????????????D.?25
4.如图,在正方形ABCD中,AB=6,点Q是AB边上的一个动点(点Q不与点B重合),点M,N分别是DQ,BQ的中点,则线段MN=(?? )
A.?32????????????????????????????????????????B.?322????????????????????????????????????????C.?3????????????????????????????????????????D.?6
5.如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为10.5,则AB的长为(?? )
A.?3 2????????????????????B.?19???????????????????????C.?2 5???????????????????????D.?26
6.如图,在正方形 ABCD 中,E为 DC 边上的一点,沿线段 BE 对折后,若 ∠ABF 比 ∠EBF 大 15° ,则 ∠EBF 的度数为( )
A.?15°??????????????????B.?20°???????????????????????C.?25°?????????????????????????D.?30°
7.如图, △ ABE、 △ BCF、 △ CDG、 △ DAH是四个全等的直角三角形,其中,AE=5,AB=13,则EG的长是( )
A.?7 2??????????????????B.?6 2????????????????????????C.?7????????????????????????D.?7 3
8.如图,在 △ABC 中, ∠ACB=90° ,以 △ABC 的各边为边分别作正方形 BAHI ,正方形 BCFG 与正方形 CADE .延长 BG , FG 分别交 AD , DE 于点K,J,连结 DH , IJ .图中两块阴影部分面积分别记为 S1 , S2 ,若 S1:S2=1:4 ,四边形 SBAHE=18 ,则四边形 MBNJ 的面积为(?? )
A.?5????????????????????????????????B.?6??????????????????????C.?8??????????????????????????D.?9
9.由四个全等的直角三角形和一个小正方形组成的大正方形 ABCD 如图所示.过点 D 作 DF 的垂线交小正方形对角线 EF 的延长线于点 G ,连结 CG ,延长 BE 交 CG 于点 H .若 AE=2BE ,则 CGBH 的值为(?? )
A.?32???????????????????????????B.?2??????????????????????C.?3107???????????????????????D.?355
10.如图,正方形 ABCD 中,在 AD 的延长线上取点 E , F ,使 DE=AD , DF=BD ,连接 BF 分别交 CD , CE 于 H , G ,下列结论:① HF=2HG ;② ∠GDH=∠GHD ;③图中有8个等腰三角形;④ S△CDG=S△DNF .其中正确的结论个数是(?? )
A.?1个??????????????????????B.?2个????????????????????????????C.?3个??????????????????????D.?4个
二、填空题
11.如图,若该正方形ABCD边长为10,将正方形沿着直线MN翻折,使得BC的对应边 B'C' 恰好经过点A , 过点A作 AG⊥MN ,垂足分别为G , 若 AG=6 ,则 AC' 的长度为________.
12.已知直角三角形ABC,∠ABC=90°,AB=3,BC=5,以AC为边向外作正方形ACEF,则这个正方形的中心O到点B的距离为________.
13.如图,矩形纸片ABCD,AD=2AB=4,点F在线段AD上,将△ABF沿BF向下翻折,点A的对应点E落在线段BC上,点M,N分别是线段AD与线段BC上的点,将四边形CDMN沿MN向上翻折,点C恰好落在线段BF的中点C'处,则线段MN的长为________.
14.如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1 , 再以对角线OB1为边作第三个正方形OB1B2C2 , 照此规律作下去,则点B2020的纵坐标为________
15.如图1是公园某处的几何造型,如图2是它的示意图,正方形的一部分在水平面EF下方,测得DE=2米,∠CDF=45°,露出水平面部分的材料长共合计140米(注:共8个大小一样的正方形造型,不计损耗),点B到水平面EF的距离为________米.
16.如图,正方形 ABCD 中, AB=4 ,O是 BC 边的中点,点E是正方形内一动点, OE=2 ,连接 DE ,将线段 DE 绕点D逆时针旋转 90° 得 DF ,连接 AE 、 CF .则线段 OF 长的最小值为________.
三、解答题
17.在正方形ABCD中,E是CD边上一点(CE>DE),AE,BD交于点F.
(1)如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.
求证:∠EAB=∠GHC;
(2)AE的垂直平分线分别与AD,AE,BD交于点P,M,N,连接CN.
①依题意补全图形;
图1????????????????? 备用图
②用等式表示线段AE与CN之间的数量关系,并证明.
18.问题情境:
(1)如图1,已知正方形ABCD,点E在CD的延长线上,以CE为边构造正方形CEFG,连接BE和DG,则BE和DG的关系为________。
(2)继续探究:如图2,若正方形ABCD的边长为3,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE。
①求证:DG⊥BE。
②连接BG,若AE=1,求BG长。
19.如图,点 P 为正方形 ABCD 对角线 BD 上一点, PE⊥BC 于点 E , PF⊥CD 于点 F .
(1)求证: PA=EF .
(2)若正方形 ABCD 的边长为12,求,四边形 PFCE 的周长.
20.如图
(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为________.
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);
②图3中补全图形,直接写出∠EOF的度数.
21.如图①,四边形ABCD是正方形,E是对角线BD上一点,连接AE、CE
(1)求证:AE=CE;
(2)如图②,点P是边CD上的一点,且PE⊥BD于E,连接BP,点O为BP的中点,连接OE。若∠PBC=30°,求∠POE的度数;
(3)在(2)的条件下,若OE= 2 ,求CE的长。
22.如图,已知四边形ABCD是正方形.
(1)如图1,若E、F、G分别是AB、BC、CD边上的点,AF和EG交于点O.现在提供三个关系:①AF⊥EG;②AO=FO;③AF=EG.从三个关系中选择一个作为条件,一个作为结论,形成一个真命题,完成下列填空并证明:你选择的条件是________,结论是________.(只要填写序号).
(2)如图2,点E、F分别在AD、AB上,BE⊥CF,垂足为点O,连接EF、EC,M、N分别是BF、CE的中点,MN分别交BE、CF于点G、H,求证:OG=OH;
(3)如图3,AB=3cm,E为CD边上一点,∠DAE=30°,O为AE的中点,过点O的直线分别交AD、BC于点M、N,若MN=AE,请直接写出AM的长.
23.综合与实践﹣﹣图形变换中的数学问题.
问题情境:
如图1,在Rt△ABC中,AB=5,∠ABC=90°,∠BAC=45°.将△ABC沿AC翻折得到△ADC , 然后展平,两个三角形拼成四边形ABCD .
(1)求证:四边形ABCD是正方形.
(2)初步探究:
将△ABC从图1位置开始绕点B按逆时针方向旋转角度α(0°<α<90°),得到△EBF , 其中点A , C的对应点分别是点E , F , 连接AE , FC并分别延长,交于点M . 试猜想线段AM与FM的数量关系和位置关系,并说明理由.
(3)如图3,连接DE , 当DE∥CM时,请直接写出CM的长.
答案
一、选择题
1.解:如图所示,过点E作EA⊥x轴,垂足为A , 过点F作FB⊥EA , 交AE的延长线于点B , 交y轴与点C ,
∵四边形OEFG是正方形,
∴FE=EO , ∠FEO=90°,
∴∠FEB+∠AEO=90°,∠AEO+∠AOE=90°,
∴∠FEB =∠EOA ,
∴△FEB≌△EOA ,
∴FB=EA , EB=OA ,
∵E(2,3),
∴FB=EA=3,EB=OA=2,
∵EA⊥x轴,FB⊥EA , OC⊥x轴,
∴四边形OABC是矩形,
∴BC=OA=2,
∴FC=FB-BC=1,BA=EB+EA=5,
∵点F在第二象限,
∴点F(-1,5)
故答案为:A .
2.解:∵四边形ABCD是正方形,
∴AB∥CD,∠A=90°,
∴∠EFD=∠BEF=60°,
∵将四边形EBCF沿EF折叠,点B恰好落在AD边上,
∴∠BEF=∠FEB'=60°,BE=B'E,
∴∠AEB'=180°﹣∠BEF﹣∠FEB'=60°,
∴B'E=2AE,
设BE=x,则B'E=x,AE=3﹣x,
∴2(3﹣x)=x,
解得x=2.
故答案为:D.
3.解:连接DD′,当等腰Rt△ADC在射线CA上运动时,点D运动轨迹为直线DD',
∵AB∥C′D′,且AB=C′D′,
∴四边形ABC′D′为平行四边形,
∴BD′+BC′=D′B+D′A,
将点B关于直线l对称到点B′,BD′+BC′=D′B+D′A= D′B′+D′A≥AB′,当D′、B′、A三点共线时,BC′+BD′的最小,最小值为AB′长,
作A′′B′⊥AD交AD延长线于点A′′,
由对称可知,BD′=BD,∠ADB=∠AD B′,∠BAD=∠B′A′′D,
∴△BAD≌△B′A′′D,
∴A′′D=AD=2,A′′B′=AB=2,
AB′= AA''2+B'A''2= 25 ,
?故答案为:D.
4.解:连接 BD ,如图,
∵四边形ABCD是正方形,
∴AB=AD=6,
∴ BD=AB2+AD2=62 ,
当点Q在AB边上运动时(点Q不与点B重合),MN一直是△BQD的中位线,
则线段 MN=12BD=32 .
故答案为:A.
5.解:∵四边形ABGF是正方形,
∴∠FAB=∠AFG=∠ACB=90°,
∴∠FAC+∠BAC=∠FAC+∠ABC=90°,
∴∠FAC=∠ABC,
在△FAM与△ABN中,
{∠F=∠NAB=90°∠FAM=∠ABNAF=AB ,
∴△FAM≌△ABN(AAS),
∴S△FAM=S△ABN ,
∴S△ABC=S四边形FNCM ,
∵在△ABC中,∠ACB=90°,
∴AC2+BC2=AB2 ,
∵AC+BC=6,
∴(AC+BC)2=AC2+BC2+2AC?BC=36,
∴AB2+2AC?BC=36,
∵AB2﹣2S△ABC=10.5,
∴AB2﹣AC?BC=10.5,
∴3AB2=57,
解得AB= 19 或﹣ 19 (负值舍去).
故答案为:B.
6.解:∵∠FBE是∠CBE折叠形成,
∴∠FBE=∠CBE,
∵∠ABF-∠EBF=15°,∠ABF+∠EBF+∠CBE=90°,
∴∠EBF=25°,
故答案为:C.
7.解:在Rt△ABE中,AE=5,AB=13,
由勾股定理得,BE= AB2-AE2 = 132-52 =12,
∵△ABE、△BCF、△CDG、△DAH是四个全等的直角三角形,
∴∠AEB=∠BFC=∠CGD=90°,BF=CG=DH=AE=5,
∴∠FEB=∠EFC=∠FGD=90°,EF=EH=12﹣5=7,
∴四边形EFGH为正方形,
∴EG= 72+72 =7 2 ,
故答案为:A.
8.解:∵ S1:S2=1:4
∴ GJBC=12
∵四边形 BCFG 与四边形 CADE 是正方形
∴ BC=FC=FG=GB=2GJ
∴ AC=AD=DE=CE=BC+GJ=3GJ
∵ ∠ACB=90°
∴ AB=AC2+BC2=13GJ
∵ AH=AB , ∠ADH=180°-∠ADE=90°
∴ HD=AH2-AD2=2GJ
∵四边形 SBAHE=S△AHD +梯形 SADEB=18
∴ 12AD×HD+12(AD+BE)×DE=12×3GJ×2GJ+12(3GJ+GJ)×3GJ=18
∴ GJ=2
∴ AF=AC-FC=3GJ-2GJ=GJ=BE
∵ ∠CAB+∠ABC=90° , ∠ABC+∠EBM=180°-∠ABI=90°
∴ ∠CAB=∠EBM ,即 ∠FAN=∠EBM
∵四边形 BCFG 与四边形 CADE 是正方形
∴ ∠AFN=180°-∠CFN=90° , ∠BEM=90°
∴ {∠AFN=∠BEM=90°AF=BE∠FAN=∠EBM
∴ △FAN≌△EBM
∴ S△FAN=S△EBM
∴ S△ABC= 四边形 SCFNB+S△EBM
∵ ∠FCE=∠CEJ=∠EJF=∠JFC=90°
∴四边形 CFJE 是矩形
∴矩形 SCFJE= 四边形 SMBNJ+ 四边形 SCFNB+S△EBM= 四边形 SMBNJ+S△ABC
∴四边形 SMBNJ = 矩形 SCFJE- S△ABC =JE×CE-12AC×BC=2GJ×3GJ-12×3GJ×2GJ=6
故答案为:B.
9.如图,设BH交CF于P,CG交DF于Q,
∵由四个全等的直角三角形和一个小正方形组成的大正方形 ABCD ,
∴BE=PC=DF,AE=BP=CF,
∵ AE=2BE ,
∴BE=PE=PC=PF=DF,
∵∠CFD=∠BPC,
∴DF//EH,
∴PH为△CFQ的中位线,
∴PH= 12 QF,CH=HQ,
∵四边形EPFN是正方形,
∴∠EFN=45°,
∵GD⊥DF,
∴△FDG是等腰直角三角形,
∴DG=FD=PC,
∵∠GDQ=∠CPH=90°,
∴DG//CF,
∴∠DGQ=∠PCH,
在△DGQ和△PCH中, {∠GDQ=∠CPHDG=PC∠DGQ=∠PCH ,
∴△DGQ≌△PCH,
∴PH=DQ,CH=GQ,
∴PH= 13 DF= 13 BE,CG=3CH,
∴BH=BE+PE+PH= 73BE ,
在Rt△PCH中,CH= PC2+PH2=BE2+(13BE)2 = 103BE ,
∴CG= 10 BE,
∴ CGBH=10BE73BE=3107 .
故答案为:C.
10.解:∵DF=BD ,
∴∠DFB=∠DBF
∵四边形ABCD是正方形,
∵AD//BC , AD=BC=CD , ∠ADB=∠DBC=45°,
∴DE//BC , ∠DFB=∠GBC ,
∵DE=AD ,
∴DE=BC ,
∴四边形DBCE是平行四边形,
∴∠DEC=∠DBC=45°,
∴∠DEC=∠ADB=∠DFB+∠DBF=2∠EFB=45°,
∴∠GBC=∠EFB=22.5°,∠CGB=∠EGF=22.5°=∠GBC ,
∴CG=BC=DE ,
∵BC=CD ,
∴DE=CD=CG ,
∴∠DEG=∠DCE=45°,EC= 2 CD , ∠CDG=∠CGD= 12 (180°-45°)=67.5°,
∴∠DGE=180°-67.5°=112.5°,
∵∠GHC=∠CDF+∠DFB=90°+22.5°=112.5°,
∴∠GHC=∠DGE ,
∴△CHG≌△EGD(AAS),
∴∠EDG=∠CGB=∠CBF ,
∴∠GDH=90°-∠EDG , ∠GHD=∠BHC=90°-∠CGB ,
∴∠GDH=∠GHD ,
∴∠GDH=∠GHD , 故②符合题意;
∵∠EFB=22.5°,
∴∠DHG=∠GDH=67.5°,
∴∠GDF=90°-∠GDH=22.5°=∠EFB ,
∴DG=GF ,
∴HG=DG=GF ,
∴HF=2HG , 即EC≠HF=2HG , 故①符合题意;
∵△CHG≌△EGD ,
∴S△CHG=S△EGD ,
∴ SΔCHG+SΔDHG=SΔEGD+sΔDHG ,即 SΔCDG=SΔCDG≠SΔDHF ,故④不符合题意;
结合前面条件易知等腰三角形有:△ABD、△CDB、△BDF、△CDE、△BCG、△DGH、△EGF、△CDG、△DGF共9个,故③不符合题意;
则正确的个数有2个.
故答案为:B .
二、填空题
11.延长AG交BC于点E ,
则 EG=AG=6 ,
∴AE=12 .
∵正方形ABCD边长为10,
AB=BC=10 .
在 Rt△ABE 中, BE=AE2-AB2=122-102=211 ,
∴CE=BC-BE=10-211 ,
由折叠的性质得, AC'=CE=10-211 ,
故答案为: 10-211 .
12.如图,延长BA到D,使AD=BC,连接OD,OA,OC,
∵四边形ACEF是正方形,∴∠AOC=90°,CO=AO,
∵∠ABC=90°,∠ABC+∠AOC=180°,
∴∠BCO+∠BAO=180°,∠BCO=∠DAO,
在△BCO与△DAO中, {BC=AD∠BCO=∠DAOCO=AO
∴△BCO≌△DAO(SAS),
∴OB=OD,∠BOC=∠DOA,∴∠BOD=∠COA=90°,
∴△BOD是等腰直角三角形,∴BD= 2OB ,
∵BD=AB+AD=AB+BC=8,∴OB= 42 .
故答案为 42 .
13.解:作C'G⊥BC,连接C'C交MN于点K,连接CM
根据题意可得,四边形ABEF为正方形,△BGE为等腰三角形
∴C'G=12×2=1,CG=4-BG=4-1=3
设CN=C'N=x,则GN=3-x
在直角三角形C'GN中,1+(3-x)2=x2 , 解得x=53
∴CN=53
在直角三角形CC'G中,CC'=32+12=10
由折叠可得,CK=CC'2=102 , CK⊥MN
∵12MN×ck=12CN×CD
∴MN=CN×CDCK=2103
14.解: ∵正方形OABC边长为1,
∴OB=2 ,
∵正方形OBB1C1是正方形OABC的对角线OB为边,
∴OB1=2,
∴B1点坐标为(0,2),
同理可知OB2=22 ,
∴B2点坐标为(-2,2),
同理可知OB3=4,B3点坐标为(-4,0),
B4点坐标为(-4,-4),B5点坐标为(0,-8),
B6(8,-8),B7(16,0)
B8(16,16),B9(0,32),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的2倍,
∵2020÷8=252…4,
∴B2020的纵横坐标符号与点B4的相同,纵坐标为负数,横坐标是正数,
∴ 点B2020的纵坐标为 -21010.
15.解:如图,延长AE、CD交于一点G,连接BG交EF于H,
∴∠EGD=90°,
∵DE=2,∠CDF=45°,
∴GD=EG=2 ,
设正方形的边长为a,则AE=CD=a-2 ,
∴2AE+2AB=4a-22=1408 ,
解得a=35+428 ,
∴BG=2a=352+88 ,
∴BH=BG-HG=352+88-1=3528 ,
故答案为:3528.
16.如图,连接DO,将线段DO绕点D逆时针旋转90°得DM,连接OF,FM,OM,
∵ ∠EDF= ∠ODM=90°,
∴ ∠EDO=∠FDM,
在△EDO与△FDM中, {DE=DF∠EDO=∠FDMDO=DM
∴ △EDO≌△FDM (SAS) ,
∴ FM=OE=2,
∵正方形ABCD中,
AB=4,O是BC边的中点,
∴ OC=2,
∴ OD=42+22=25
∴ OM=(25)2+(25)2=210
∵OF+MF ≥ OM,
∴ OF≥210-2
∴线段OF长的最小值为 210-2
故答案为: 210-2
三、解答题
17.(1)证明:在正方形ABCD中,AD∥BC,∠BAD=90°,
∴∠AGH=∠GHC.
∵GH⊥AE,
∴∠EAB=∠AGH.
∴∠EAB=∠GHC.
(2)①补全图形,如图所示.
② AE=2CN .
证明:连接AN,连接EN并延长,交AB边于点Q.
∵四边形ABCD是正方形,
∴点A,点C关于BD对称.
∴NA=NC,∠1=∠2.
∵PN垂直平分AE,
∴NA=NE.
∴NC=NE.
∴∠3=∠4.
在正方形ABCD中,BA∥CE,∠BCD=90°,
∴∠AQE=∠4.
∴∠1+∠AQE=∠2+∠3=90°.
∴∠ANE=∠ANQ=90°.
在Rt△ANE中,
∴ AE=2CN .
18.(1)BE= DG,BE⊥DG
(2)①如图2,延长BE, GD交于点H,
∵四边形ABCD是正方形,四边形CEFG是正方形,
∴BC=CD,∠BCD=∠ECG=90°,CE= CG,
∴∠BCE=∠DCG,
∴△BCE≌△DCG(SAS),
∴∠BEC=∠DGC,
∵∠BEC+∠HEC= 180°,
∴∠DGC+∠HEC=180°,
∵∠DGC+∠HEC+ CECG+∠DHE = 360°,
∴∠DHE=90°,
∴DG⊥BE;
②如图3,过点G作GN⊥BC,交BC延长线于点N,
∵AE= 1,AD=3,
∴DE= 2,
∵∠ECG=∠DCN= 90°,
∴∠ECD=∠GCN
又∵EC=CG,∠EDC=∠N=90°,
∴△ECD≌△GCN(AAS),
∴DE=GN=2,CN=CD=3,
∴BN= BC+ CN= 6,
∴BG= BN2+CN2 = 62+22 = 210
解:(1)如图1,延长GD交BE于点H,
∵四边形ABCD是正方形,四边形CEFG是正方形,
∴BC=CD,∠BCD=∠ECG=90°,CE=CG,
∴△BCE≌△DCG(SAS),
∴BE=DG,∠BEC=∠DGC,
∵∠BEC+∠EBC=90°,
∴∠DGC+∠EBC=90°,
∴∠BHG=90°,
∴BE⊥DG;
19.(1)证明:连接PC,
∵四边形ABCD是正方形,
∴AB=CB,∠ABD=∠CBD=45°,∠BCD=90°,
在△ABP与△CBP中,
{AB=CB∠ABD=∠CBDPB=PB ,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PE⊥CD,PF⊥BC,
∴∠PFC=90°,∠PEC=90°.
又∵∠BCD=90°,
∴四边形PFCE是矩形,
∴EF=PC,
∴PA=EF;
(2)解:由(1)知四边形PFCE是矩形,
∴PE=CF,PF=CE,
又∵∠CBD=45°,∠PEB=90°,
∴BE=PE,
又∵BC=12,
∴矩形PFCE的周长为2(PE+EC)=2(BE+EC)=2BC=24.
20.(1)3
(2)解:①如图2,在AD上截取AH=DE,连接EH,作EH的垂直平分线,交DH于F,连接EF,则△EDF就是所求作的三角形.
②如图3,连接OD、OA、OH,
∵O为正方形的中心,
∴OA=OD,∠DOA=90°,
在△AHO和△DEO中,
{AO=OD∠1=∠2AH=DE ,
∴△AHO≌△DEO(SAS),
∴OE=OH,∠4=∠3,
∴∠EOH=∠DOA=90°,
∵OF是EH的垂直平分线,
∴EF=FH,
在△EOF和△HOF中,
{OE=OHOF=OFEF=FH ,
∴△EFO≌△HOF(SSS),
∴∠EOF=∠HOF,
∵∠EOH=∠DOA=90°.
∴∠EOF=45°
解:(1)∵AB的垂直平分线交AC于点D,
∴BD=AD,
∴△BCD的周长=BC+CD+BD=BC+AC=1+2=3,
故答案为:3;
21.(1)证明:∵ 四边形ABCD是正方形 ,
∴AB=BC,∠ABE=∠CBE,BE=BE
∴△ABE≌△CBE(SAS)
∴AE=CE
(2)解:
∵ 四边形ABCD是正方形 ,
∴∠EBC=∠EDP=45°
∵ ∠PBC=30°,
∴∠EBP=15°
∵ PE⊥BD,点O为BP的中点,
∴OE=OB=OP
∴∠OEB=∠EBP=15°
∴∠POE=∠OEB+∠EBP=30°
(3)连接OC,
∵点O为BP的中点,∠BCP=90°
∴OB=OC
∴∠OBC=∠OCB=30°
∴∠POC=∠OBC+∠OCB=60°
∴∠EOC=∠POE+∠POC=90°,
∵OE=OB=OC=2
∴CE=OC2+OE2=2
22. (1)①;③
(2)证明:取EF中点Q,连接QN,QM,
∴ QN//FC,QN=12FC,MQ//BE,MQ=12BE,
由(1)知当BE⊥CF时BE=CF,
∴NQ=MQ,∠QNM=∠QMN,
∵∠QMN=∠OGH,∠QNM=∠OHG,
∴∠OGH =∠OHG,
∴OG=OH;
(3)解:AM=2,
过M作MK⊥BC,
由(1)同理可证△MNK ? △AED,
∴AE⊥MN,∠AOM=90°,
∵AB=3,∠DAE=30°,
∴AD=3,
设DE=x,AE=2x,
则根据勾股定理可得: AE=23 , DE=3 ,
∵O为AE中点,
∴ AO=12AE=3 ,
同理可得:AM=2.
(1)①;③
?证明:过点G作GH⊥AB于H,
由题意知GH=AD=AB,∠GHE=∠B=90°,有∠BAF+∠AFB=90°,
∵AF⊥GE,
∴∠AOE=90°,
∴∠BAF+∠AEG=90°,
∴∠AFB=∠AEG,
∴△AFB ? △GEH(ASA),
∴AF=EG;
23.(1)解:
∵∠ABC=90°,∠BAC=45°,
∴∠BCA=90°﹣45°=45°,
∴∠BAC=∠BCA,
∴AB=BC,
∴△ABC是等腰三角形,
∵△ABC沿AC翻折得到△ADC,
∴△ABC≌△ADC,
∴AD=AB,CD=BC,
∴AB=AD=CD=BC,
∴四边形ABCD是菱形,
∵∠B=90°,
∴四边形ABCD是正方形.
?(2)解:
由旋转可知,△ABC≌△EBF,
∴AB=BE,BC=BF,AC=EF,∠ABE=∠CBF=α,
在△ABE和△CBF中, {AB=BC∠ABE=∠CBFBE=BF ,
∴△ABE≌△CBF(SAS),
∴∠AEB=∠BFC,AE=CF,
∵AB=BC,
∴AB=BE=BC=BF,
∴∠BCF=∠BFC,
∴∠AEB=∠BCF,
∵∠BEF=∠ACB=45°,∠AEB=∠BCF,
∴180°﹣(∠AEB+∠BEF)=180°﹣(∠BCF+∠ACB),
∴∠FEM=∠ACM,
在△ACM和△FEM中, {∠FEM=∠ACM∠M=∠MAC=FE ,
∴△ACM≌△FEM(AAS),
∴AM=FM,∠MAC=∠MFE,
∵∠DAC=∠DCA=45°,
∴∠MAC=45°﹣∠DAM,∠MCA=45°+∠MCD,
∴∠DAM=∠MCD,
∴∠MAC+∠ACM=45°﹣∠DAM+45°+∠MCD=90°,
∴∠M=90°,
∴AM⊥FM,
故答案为:AM⊥FM且AM=FM.
深入探究:
(3)CM= 5
解:(3)取AC的中点G , 连接EG , BG ,
?
∵DE∥CM ,
∴∠DEM=∠M=90°,
∵AG=GE= 52 ,AB=BE ,
在△BAG和△BEG中, {BG=BGAB=BEAG=EG ,
∴△BAG≌△BEG(SSS),
∠BEG=∠BAG=90°,∠GBA+∠GBE= α2 ,
∵∠EBA=α ,
∴∠EAB= 180°-α2 ,
∴∠ABG+∠BAE= α2 + 180°-α2 =90°,
∴BG⊥AE ,
∵AB=5,AG= 52 ,
∴BG= 552 ,
∴ 12 AE? 552 = 12 ×2×5× 52 ,
解得:AE=2 5 ,
设CM=ME=x ,
在Rt△ACM中,x2+(x+2 5 )2=(5 2 )2 ,
∵x>0,
∴x= 5 ,
故CM= 5 .
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
