新疆乌市第四高中2020-2021学年高二下学期期末考试数学(文)试卷 Word版含答案
文档属性
| 名称 | 新疆乌市第四高中2020-2021学年高二下学期期末考试数学(文)试卷 Word版含答案 |
|
|
| 格式 | doc | ||
| 文件大小 | 540.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 00:00:00 | ||
图片预览


文档简介
乌市第四高中2020-2021学年高二下学期期末考试
数学试题(文科)
一、选择题:(每题5分,共12题)
1. 若复数满足,则( )
A. B. C. D.
2. 若全集,集合,则( )
A. B. C. D.
3. 若f(x)=2xf′(1)+x2,则f′(0)等于( )
A.2 B.0 C.-2 D.-4
4. 下列函数中,既是偶函数又在区间(0,+ ∞)上单调递减的是 ( )
A. B. C. D.
5. 已知a为函数f(x)=x3-12x的极小值点,则a=( )
A.-4 B.-2 C.4 D.2
6. 命题“?x>0,都有x2-x≤0”的否定是( )
A.?x>0,使得x2-x≤0 B.?x>0,使得x2-x>0
C.?x>0,都有x2-x>0 D.?x≤0,都有x2-x>0
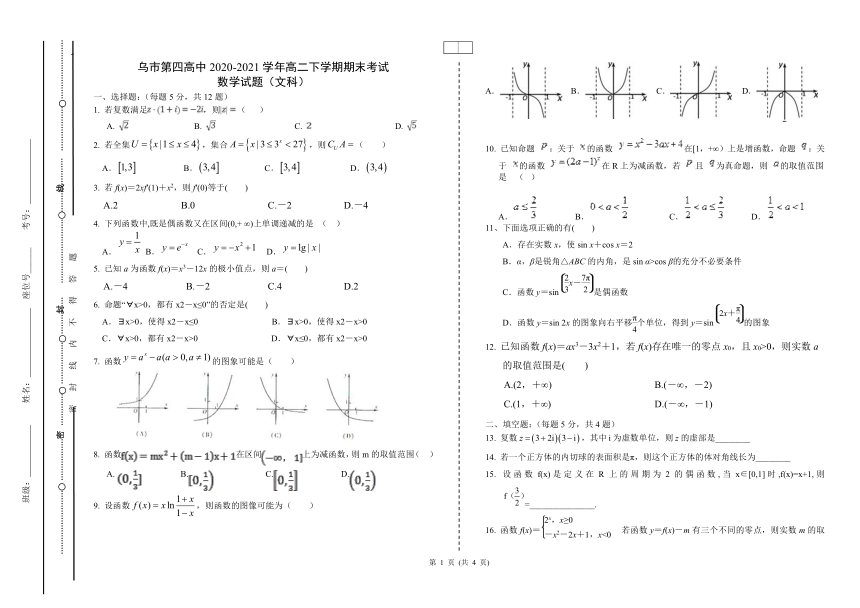
7. 函数的图象可能是( )
8. 函数在区间上为减函数,则m的取值范围( )
A. B. C. D.
9. 设函数,则函数的图像可能为( )
A. B. C. D.
10. 已知命题 :关于 的函数 在[1,+∞)上是增函数,命题 :关于 的函数 在R上为减函数,若 且 为真命题,则 的取值范围是????(???)
A. B. C. D.
11、下面选项正确的有( )
A.存在实数x,使sin x+cos x=2
B.α,β是锐角△ABC的内角,是sin α>cos β的充分不必要条件
C.函数y=sin是偶函数
D.函数y=sin 2x的图象向右平移个单位,得到y=sin的图象
12. 已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则实数a的取值范围是( )
A.(2,+∞) B.(-∞,-2)
C.(1,+∞) D.(-∞,-1)
二、填空题:(每题5分,共4题)
13. 复数,其中为虚数单位,则的虚部是________
14. 若一个正方体的内切球的表面积是π,则这个正方体的体对角线长为________
15. 设函数f(x)是定义在R上的周期为2的偶函数,当x∈[0,1]时,f(x)=x+1,则=_______________.
16. 函数f(x)=若函数y=f(x)-m有三个不同的零点,则实数m的取值范围是________.
三、解答题:
17. 一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
18.如图所示,四棱锥中,底面为的中点.
(1)求证:平面;
(2)求三棱锥的体积.
19. 某中学为研究学生的身体素质与体育锻炼时间的关系, 对该校300名高三学生平均每天体育锻炼的时间(单位:分钟)进行调查,得到频率分布直方图如图.将日均体育锻炼时间在[40,60)的学生评价为 “锻炼达标”。
(1)根据频率分布直方图,完成下面的2×2列联表;
锻炼达标 锻炼不达标 合计
身体素质合格
身体素质不合格
50 120
合计
300
(2)根据列联表判断,是否有99.9%的把握认为学生 “身体素质” 与 “锻炼时间”有关?
参临界值表:
P(K2≥k0) 0.10 0.05 0.010 0.001
k0 2.706 3.841 6.635 10.828
考公式:K2=,其中n=a+b+c+d.
20. 在平面直角坐标系xOy中,圆C的参数方程为
(θ为参数),直线l经过点P(1,2),倾斜角α=.
(1)写出圆C的普通方程和直线l的参数方程;
(2)设直线l与圆C相交于A,B两点,求|PA|·|PB|的值.
21. 已知,.
(1)当时,求函数的单调区间;
(2)是否存在实数,使在区间上的最小值是3,若存在,求出的值;若不存在,说明理由.
乌市第四高中2020-2021学年高二下学期期末考试
数学文科答案
选择:AADCD BCDBC CB
填空:13.3 14. 15. 3/2 16.1解答题:
17. (1)由题意,(a,b,c)所有的可能的结果有33=27(种).
设“抽取的卡片上的数字满足a+b=c”为事件A,
则事件A包括(1,1,2),(1,2,3),(2,1,3),共3种.
所以P(A)==.
因此,“抽取的卡片上的数字满足a+b=c”的概率为.
(2)设“抽取的卡片上的数字a,b,c不完全相同”为事件B,
则事件B包括(1,1,1),(2,2,2),(3,3,3),共3种.
所以P(B)=1-P(B)=1-=.
因此,“抽取的卡片上的数字a,b,c不完全相同”的概率为.
18. (1)见证明;(2).
(1)证明:∵,
,.
在中,
∴,∴是直角三角形.
又为的中点,∴,
∴是等边三角形,∴,
∴,∴.
又平面平面,∴平面.
(2)解:
∵底面,∴底面,
∴为三棱锥的高.
∵,∴.
又
∴,
∴.
19. 解:(1)由频率分布直方图可知,“锻炼达标”的人数为300×(0.03+0.04)×10=210.
补充完整的2×2列联表如下:
锻炼达标 锻炼不达标 合计
身体素质合格 140 40 180
身体素质不合格 70 50 120
合计 210 90 300
(2)K2==≈12.963>10.828,
故有99.9%的把握认为学生“身体素质”与“锻炼时间”有关
20. (1)由消去θ,
得圆C的普通方程为x2+y2=16.
又直线l过点P(1,2),且倾斜角α=.
所以l的参数方程为
即(t为参数).
(2)把直线l的参数方程代入x2+y2=16,
得+=16,t2+(+2)t-11=0,
所以t1t2=-11.
由参数方程的几何意义,|PA|·|PB|=|t1t2|=11.
21. 略
第 3 页 (共 4 页)
数学试题(文科)
一、选择题:(每题5分,共12题)
1. 若复数满足,则( )
A. B. C. D.
2. 若全集,集合,则( )
A. B. C. D.
3. 若f(x)=2xf′(1)+x2,则f′(0)等于( )
A.2 B.0 C.-2 D.-4
4. 下列函数中,既是偶函数又在区间(0,+ ∞)上单调递减的是 ( )
A. B. C. D.
5. 已知a为函数f(x)=x3-12x的极小值点,则a=( )
A.-4 B.-2 C.4 D.2
6. 命题“?x>0,都有x2-x≤0”的否定是( )
A.?x>0,使得x2-x≤0 B.?x>0,使得x2-x>0
C.?x>0,都有x2-x>0 D.?x≤0,都有x2-x>0
7. 函数的图象可能是( )
8. 函数在区间上为减函数,则m的取值范围( )
A. B. C. D.
9. 设函数,则函数的图像可能为( )
A. B. C. D.
10. 已知命题 :关于 的函数 在[1,+∞)上是增函数,命题 :关于 的函数 在R上为减函数,若 且 为真命题,则 的取值范围是????(???)
A. B. C. D.
11、下面选项正确的有( )
A.存在实数x,使sin x+cos x=2
B.α,β是锐角△ABC的内角,是sin α>cos β的充分不必要条件
C.函数y=sin是偶函数
D.函数y=sin 2x的图象向右平移个单位,得到y=sin的图象
12. 已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则实数a的取值范围是( )
A.(2,+∞) B.(-∞,-2)
C.(1,+∞) D.(-∞,-1)
二、填空题:(每题5分,共4题)
13. 复数,其中为虚数单位,则的虚部是________
14. 若一个正方体的内切球的表面积是π,则这个正方体的体对角线长为________
15. 设函数f(x)是定义在R上的周期为2的偶函数,当x∈[0,1]时,f(x)=x+1,则=_______________.
16. 函数f(x)=若函数y=f(x)-m有三个不同的零点,则实数m的取值范围是________.
三、解答题:
17. 一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
18.如图所示,四棱锥中,底面为的中点.
(1)求证:平面;
(2)求三棱锥的体积.
19. 某中学为研究学生的身体素质与体育锻炼时间的关系, 对该校300名高三学生平均每天体育锻炼的时间(单位:分钟)进行调查,得到频率分布直方图如图.将日均体育锻炼时间在[40,60)的学生评价为 “锻炼达标”。
(1)根据频率分布直方图,完成下面的2×2列联表;
锻炼达标 锻炼不达标 合计
身体素质合格
身体素质不合格
50 120
合计
300
(2)根据列联表判断,是否有99.9%的把握认为学生 “身体素质” 与 “锻炼时间”有关?
参临界值表:
P(K2≥k0) 0.10 0.05 0.010 0.001
k0 2.706 3.841 6.635 10.828
考公式:K2=,其中n=a+b+c+d.
20. 在平面直角坐标系xOy中,圆C的参数方程为
(θ为参数),直线l经过点P(1,2),倾斜角α=.
(1)写出圆C的普通方程和直线l的参数方程;
(2)设直线l与圆C相交于A,B两点,求|PA|·|PB|的值.
21. 已知,.
(1)当时,求函数的单调区间;
(2)是否存在实数,使在区间上的最小值是3,若存在,求出的值;若不存在,说明理由.
乌市第四高中2020-2021学年高二下学期期末考试
数学文科答案
选择:AADCD BCDBC CB
填空:13.3 14. 15. 3/2 16.1
17. (1)由题意,(a,b,c)所有的可能的结果有33=27(种).
设“抽取的卡片上的数字满足a+b=c”为事件A,
则事件A包括(1,1,2),(1,2,3),(2,1,3),共3种.
所以P(A)==.
因此,“抽取的卡片上的数字满足a+b=c”的概率为.
(2)设“抽取的卡片上的数字a,b,c不完全相同”为事件B,
则事件B包括(1,1,1),(2,2,2),(3,3,3),共3种.
所以P(B)=1-P(B)=1-=.
因此,“抽取的卡片上的数字a,b,c不完全相同”的概率为.
18. (1)见证明;(2).
(1)证明:∵,
,.
在中,
∴,∴是直角三角形.
又为的中点,∴,
∴是等边三角形,∴,
∴,∴.
又平面平面,∴平面.
(2)解:
∵底面,∴底面,
∴为三棱锥的高.
∵,∴.
又
∴,
∴.
19. 解:(1)由频率分布直方图可知,“锻炼达标”的人数为300×(0.03+0.04)×10=210.
补充完整的2×2列联表如下:
锻炼达标 锻炼不达标 合计
身体素质合格 140 40 180
身体素质不合格 70 50 120
合计 210 90 300
(2)K2==≈12.963>10.828,
故有99.9%的把握认为学生“身体素质”与“锻炼时间”有关
20. (1)由消去θ,
得圆C的普通方程为x2+y2=16.
又直线l过点P(1,2),且倾斜角α=.
所以l的参数方程为
即(t为参数).
(2)把直线l的参数方程代入x2+y2=16,
得+=16,t2+(+2)t-11=0,
所以t1t2=-11.
由参数方程的几何意义,|PA|·|PB|=|t1t2|=11.
21. 略
第 3 页 (共 4 页)
同课章节目录
