新疆乌市第四高中2020-2021学年高一下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 新疆乌市第四高中2020-2021学年高一下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 995.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 08:13:41 | ||
图片预览

文档简介
乌市第四高中2020-2021学年高一下学期期末考试
数学试题
一、选择题:(每题5分,共12题)
1. 直线的倾斜角为( )
A. B. C. D.
2. 如果直线与直线平行,则的值为( )
A. B. C. D.
3. 已知两条直线,两个平面,给出下面四个命题:
① ②
③ ④
其中正确命题的序号是( )
A. ①③ B. ②④ C.①④ D.②③
4.直线与圆的位置关系是( )
A.相交 B. 相切 C. 相离 D.不确定
5. 若向量,,则与共线的向量可以是( )
A. B. C. D.
6. 在△ABC中,已知,则B等于( )
A.30° B.60° C.30°或150° D.60°或120°
7. 已知等差数列的前n项和为,若,则等于( )
A.8 B.16 C.24 D.32
8.下列说法中,错误的是( )
A. 平行于同一直线的两个平面平行
B. 平行于同一平面的两个平面平行
C. 一个平面与两个平行平面相交,交线平行
D. 一条直线与两个平行平面中的一个相交,则必与另一个相交
9. a,b,c是两两不同的三条直线,下面四个命题中,真命题是( )
A.若直线a,b异面,b,c异面,则a,c异面
B.若直线a,b相交,b,c相交,则a,c相交
C.若a∥b,则a,b与c所成的角相等
D.若a⊥b,b⊥c,则a∥c
10. 已知一个几何体的三视图如图所示,则该几何体的侧面积为( )
A.28π B. C.20π D.12π
11. 在正方体中,P为的中点,则直线PB与所成的角为( )
B. C. D.
12. 若四面体棱长都相等,则相邻两侧面所成的二面角的余弦值为( )
A. B. C. D.
二、填空题:(每题5分,共4题)
13. 若一个正方体的内切球的表面积是π,则这个正方体的体对角线长为________
14. 已知点,直线,点M关于直线的对称点Q的坐标是___________
15. 点(x,y)在直线x+2y=3上移动,2x+4y的最小值是__________
16. 已知线段AB的端点,直线过原点且与线段AB不相交,则直线的斜率的取值范围是__________________
三、解答题:(共5题)
17.(10分)
已知两条直线:,为何值时,与:
(1)垂直;
(2)平行.
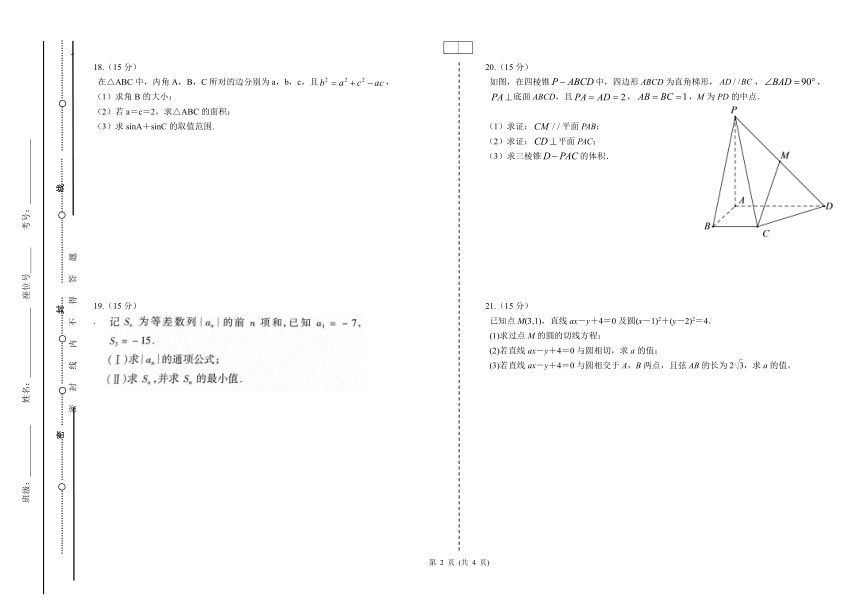
18.(15分)
在△ABC中,内角A,B,C所对的边分别为a,b,c,且,
(1)求角B的大小;
(2)若a=c=2,求△ABC的面积;
(3)求sinA+sinC的取值范围.
19.(15分)
.
20.(15分)
如图,在四棱锥中,四边形ABCD为直角梯形,,,底面ABCD,且,,M为PD的中点.
(1)求证:平面PAB;
(2)求证:平面PAC;
(3)求三棱锥的体积.
21.(15分)
已知点M(3,1),直线ax-y+4=0及圆(x-1)2+(y-2)2=4.
(1)求过点M的圆的切线方程;
(2)若直线ax-y+4=0与圆相切,求a的值;
(3)若直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2,求a的值。
乌市第四高中2020-2021学年高一下学期期末考试
数学答案
一、选择答案:ABDAB ABACC DB
二、填空答案: 13. 14. (3,4) 15. 4. 16. (-∞,-4)∪(,+∞)
三、解答题:
17. 当时,,此时与不平行也不垂直,
当时,直线的斜率,直线的斜率
(1)由得,所以
(2)由得,即,所以或,
当时,此时与重合,不符,舍去;
当时,,此时,符合
综上所述,.
18. (Ⅰ)由.,得,
所以;
(Ⅱ)由(Ⅰ)得 .
(Ⅲ)由题意得 .
因为0<A<,
所以.
故所求的取值范围是.
19. (1)an=2n-9
(2)Sn=n(n-8)
Sn最小值-16
20.
(1)若E为PA中点,连接EM、EB,由M为PD的中点,
∴且,又且,即且,
∴四边形为平行四边形,故,
∵面,面,
∴平面PAB.
(2)连接AC,过C作交于F点,即且,
∴中,,而在中,,有,
∴,又面ABCD,面,则,
∵,
∴面.
(3)由(2)知,是三棱锥的高,而,
∴.
21.(本小题满分12分)
(1)由题意知圆心的坐标为(1,2),半径r=2,
当过点M的直线的斜率不存在时,方程为x=3.
由圆心(1,2)到直线x=3的距离d=3-1=2=r知,此时,直线与圆相切.
当过点M的直线的斜率存在时,设方程为y-1=k(x-3),即kx-y+1-3k=0.
由题意知=2,解得k=.
∴方程为y-1=(x-3),即3x-4y-5=0.
故过点M的圆的切线方程为x=3或3x-4y-5=0.
(2)由题意有=2,解得a=0或a=.
(3)∵圆心到直线ax-y+4=0的距离为,
∴2+2=4,解得a=-.
第 3 页 (共 4 页)
数学试题
一、选择题:(每题5分,共12题)
1. 直线的倾斜角为( )
A. B. C. D.
2. 如果直线与直线平行,则的值为( )
A. B. C. D.
3. 已知两条直线,两个平面,给出下面四个命题:
① ②
③ ④
其中正确命题的序号是( )
A. ①③ B. ②④ C.①④ D.②③
4.直线与圆的位置关系是( )
A.相交 B. 相切 C. 相离 D.不确定
5. 若向量,,则与共线的向量可以是( )
A. B. C. D.
6. 在△ABC中,已知,则B等于( )
A.30° B.60° C.30°或150° D.60°或120°
7. 已知等差数列的前n项和为,若,则等于( )
A.8 B.16 C.24 D.32
8.下列说法中,错误的是( )
A. 平行于同一直线的两个平面平行
B. 平行于同一平面的两个平面平行
C. 一个平面与两个平行平面相交,交线平行
D. 一条直线与两个平行平面中的一个相交,则必与另一个相交
9. a,b,c是两两不同的三条直线,下面四个命题中,真命题是( )
A.若直线a,b异面,b,c异面,则a,c异面
B.若直线a,b相交,b,c相交,则a,c相交
C.若a∥b,则a,b与c所成的角相等
D.若a⊥b,b⊥c,则a∥c
10. 已知一个几何体的三视图如图所示,则该几何体的侧面积为( )
A.28π B. C.20π D.12π
11. 在正方体中,P为的中点,则直线PB与所成的角为( )
B. C. D.
12. 若四面体棱长都相等,则相邻两侧面所成的二面角的余弦值为( )
A. B. C. D.
二、填空题:(每题5分,共4题)
13. 若一个正方体的内切球的表面积是π,则这个正方体的体对角线长为________
14. 已知点,直线,点M关于直线的对称点Q的坐标是___________
15. 点(x,y)在直线x+2y=3上移动,2x+4y的最小值是__________
16. 已知线段AB的端点,直线过原点且与线段AB不相交,则直线的斜率的取值范围是__________________
三、解答题:(共5题)
17.(10分)
已知两条直线:,为何值时,与:
(1)垂直;
(2)平行.
18.(15分)
在△ABC中,内角A,B,C所对的边分别为a,b,c,且,
(1)求角B的大小;
(2)若a=c=2,求△ABC的面积;
(3)求sinA+sinC的取值范围.
19.(15分)
.
20.(15分)
如图,在四棱锥中,四边形ABCD为直角梯形,,,底面ABCD,且,,M为PD的中点.
(1)求证:平面PAB;
(2)求证:平面PAC;
(3)求三棱锥的体积.
21.(15分)
已知点M(3,1),直线ax-y+4=0及圆(x-1)2+(y-2)2=4.
(1)求过点M的圆的切线方程;
(2)若直线ax-y+4=0与圆相切,求a的值;
(3)若直线ax-y+4=0与圆相交于A,B两点,且弦AB的长为2,求a的值。
乌市第四高中2020-2021学年高一下学期期末考试
数学答案
一、选择答案:ABDAB ABACC DB
二、填空答案: 13. 14. (3,4) 15. 4. 16. (-∞,-4)∪(,+∞)
三、解答题:
17. 当时,,此时与不平行也不垂直,
当时,直线的斜率,直线的斜率
(1)由得,所以
(2)由得,即,所以或,
当时,此时与重合,不符,舍去;
当时,,此时,符合
综上所述,.
18. (Ⅰ)由.,得,
所以;
(Ⅱ)由(Ⅰ)得 .
(Ⅲ)由题意得 .
因为0<A<,
所以.
故所求的取值范围是.
19. (1)an=2n-9
(2)Sn=n(n-8)
Sn最小值-16
20.
(1)若E为PA中点,连接EM、EB,由M为PD的中点,
∴且,又且,即且,
∴四边形为平行四边形,故,
∵面,面,
∴平面PAB.
(2)连接AC,过C作交于F点,即且,
∴中,,而在中,,有,
∴,又面ABCD,面,则,
∵,
∴面.
(3)由(2)知,是三棱锥的高,而,
∴.
21.(本小题满分12分)
(1)由题意知圆心的坐标为(1,2),半径r=2,
当过点M的直线的斜率不存在时,方程为x=3.
由圆心(1,2)到直线x=3的距离d=3-1=2=r知,此时,直线与圆相切.
当过点M的直线的斜率存在时,设方程为y-1=k(x-3),即kx-y+1-3k=0.
由题意知=2,解得k=.
∴方程为y-1=(x-3),即3x-4y-5=0.
故过点M的圆的切线方程为x=3或3x-4y-5=0.
(2)由题意有=2,解得a=0或a=.
(3)∵圆心到直线ax-y+4=0的距离为,
∴2+2=4,解得a=-.
第 3 页 (共 4 页)
同课章节目录
