黑龙江省哈尔滨市重点高中2020-2021学年高二下学期6月月考数学(理)试题 Word版含答案
文档属性
| 名称 | 黑龙江省哈尔滨市重点高中2020-2021学年高二下学期6月月考数学(理)试题 Word版含答案 | 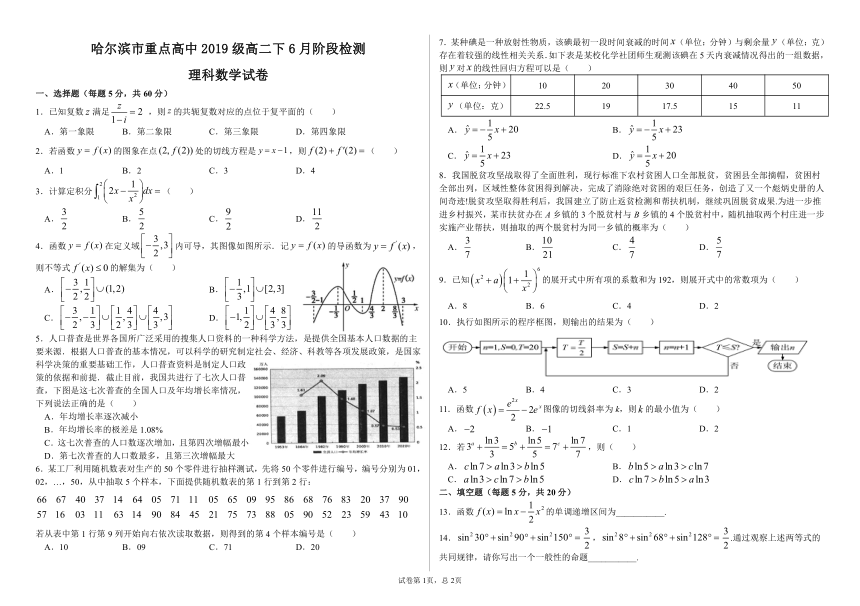 | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 16:04:42 | ||
图片预览




文档简介
哈尔滨市重点高中2019级高二下6月阶段检测
理科数学试卷
一、选择题(每题5分,共60分)
1.已知复数满足 ,则的共轭复数对应的点位于复平面的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.若函数的图象在点处的切线方程是,则( )
A.1 B.2 C.3 D.4
3.计算定积分( )
A. B. C. D.
4.函数在定义域内可导,其图像如图所示.记的导函数为,则不等式的解集为( )
A. B.
C. D.
5.人口普查是世界各国所广泛采用的搜集人口资料的一种科学方法,是提供全国基本人口数据的主要来源.根据人口普查的基本情况,可以科学的研究制定社会、经济、科教等各项发展政策,是国家科学决策的重要基础工作,人口普查资料是制定人口政策的依据和前提.截止目前,我国共进行了七次人口普查,下图是这七次普查的全国人口及年均增长率情况,下列说法正确的是( )
A.年均增长率逐次减小
B.年均增长率的极差是1.08%
C.这七次普查的人口数逐次增加,且第四次增幅最小
D.第七次普查的人口数最多,且第三次增幅最大
6.某工厂利用随机数表对生产的50个零件进行抽样测试,先将50个零件进行编号,编号分别为01,02,…,50,从中抽取5个样本,下面提供随机数表的第1行到第2行:
若从表中第1行第9列开始向右依次读取数据,则得到的第4个样本编号是( )
A.10 B.09 C.71 D.20
7.某种碘是一种放射性物质,该碘最初一段时间衰减的时间(单位:分钟)与剩余量(单位:克)存在着较强的线性相关关系.如下表是某校化学社团师生观测该碘在5天内衰减情况得出的一组数据,则对的线性回归方程可以是( )
(单位:分钟) 10 20 30 40 50
(单位:克) 22.5 19 17.5 15 11
A. B.
C. D.
8.我国脱贫攻坚战取得了全面胜利,现行标准下农村贫困人口全部脱贫,贫困县全部摘帽,贫困村全部出列,区域性整体贫困得到解决,完成了消除绝对贫困的艰巨任务,创造了又一个彪炳史册的人间奇迹!脱贫攻坚取得胜利后,我国建立了防止返贫检测和帮扶机制,继续巩固脱贫成果.为进一步推进乡村振兴,某市扶贫办在A乡镇的3个脱贫村与B乡镇的4个脱贫村中,随机抽取两个村庄进一步实施产业帮扶,则抽取的两个脱贫村为同一乡镇的概率为( )
A. B. C. D.
9.已知的展开式中所有项的系数和为192,则展开式中的常数项为( )
A.8 B.6 C.4 D.2
10.执行如图所示的程序框图,则输出的结果为( )
A.5 B.4 C.3 D.2
11.函数图像的切线斜率为k,则的最小值为( )
A. B. C.1 D.2
12.若,则( )
A. B.
C. D.
二、填空题(每题5分,共20分)
13.函数的单调递增区间为___________.
14.,.通过观察上述两等式的共同规律,请你写出一个一般性的命题___________.
15.对某种电子元件使用寿命跟踪调查,所得样本频率分布直方图如图,若一批电子元件中寿命在100~300小时的电子元件的数量为400,则寿命在500~600小时的电子元件的数量为_______.
16.已知函数.
①曲线上存在垂直于y轴的切线;②函数有四个零点;
③函数有三个极值点; ④方程有四个根.
上述结论中正确的是_______________.
三、解答题(共70分)
17.(共10分)已知函数在时有极值为
(1)求实数的值;
(2)求当 时,的最大值.
18.(共12分)某农林科技大学培育出某一小麦新品种,为检验该新品种小麦的最佳播种日期,把一块地均分为,两块试验田(假设,两块试验田地质情况一致),10月10日在试验田播种该新品种小麦,10月20日在试验田播种该新品种小麦,小麦收割后,从这两块试验田收获的小麦中各随机抽取了20份(每份1000粒),并测其千粒重(单位:),按照[20,30),[30,40),[40,50]进行分组,得到如下表格.其中千粒重不低于的小麦视为饱满,否则为不饱满.
[20,30) [30,40) [40,50]
试验田/份 4 7 9
试验田/份 7 10 3
(1)完成下面的列联表,并判断是否有95%的把握认为小麦是否饱满与播种日期有关;
10月10日播种 10月20日播种 合计
饱满
不饱满
合计
(2)用样本估计总体,从试验田随机选取50份(每份1000粒)小麦,记饱满的小麦份数为,求数学期望.
参考公式:,其中.
() 0.15 0.10 0.05 0.025 0.010 0.001
2.072 2.706 3.841 5.024 6.635 10.828
19.(共12分)在平面直角坐标系中,直线的参数方程为(为参数).以坐标原点为极点,轴非负半轴为极轴建立极坐标系,圆的极坐标方程为.
(1)求圆的标准方程.
(2)直线与圆的相交弦为,是弦上动点,求 的取值范围.
20.(共12分)如图,多面体中,平面,底面为等腰梯形,,,,,且.
(1)求证:平面;
(2)求二面角的余弦值.
21.(共12分)已知函数,其中.
(1)讨论的单调性;
(2)若有两个极值点,证明.
22.(共12分)已知椭圆的离心率为,左、右焦点分别为,,上、
下顶点分别为,四边形的面积为 .
(1)求椭圆的标准方程;
(2)点是椭圆上一动点,直线,分别与椭圆交于点,,试问:是否为定值?若是,求出该定值.
哈尔滨市重点高中2019级高二下6月阶段检测
答案
1~12
;14.;15.300;16.①③④
17.(1);(2)最大值0.
解:(1)由可得
又为极值点,所以
又极值为,即,则
可得:或
当时,,
↗ 极大值 ↘ 极小值 ↗
当时,
所以在上单调递增,无极值,综上.
(2)由(1)知,,为增函数,时,为减函数,
最大值0
18.(1)填表见解析;有;(2).
(1)补全的列联表如下:
10月10日播种 10月20日播种 合计
饱满 9 3 12
不饱满 11 17 28
合计 20 20 40
由表中的数据可得,
由于,
所以有95%的把握认为小麦是否饱满与播种日期有关.
(2)因为从试验田的样本中随机抽取1份小麦,抽到饱满小麦的概率为,
所以,
故.
19.(1);(2).
(1)由得:,
化为直角坐标方程为:,
圆的标准方程为.
(2),,
由(1)知:圆的圆心为,半径,
则由参数的几何意义知:,解得:,
的取值范围为.
20.(1)证明见解析;(2).
(1)中,,.
设,连结,
,,.
,又,所以四边形为平行四边形,
,又平面,平面,
平面.
(2)由(1)知,,,
以,,分别为x,y,z轴建立空间直角坐标系,如图所示,
则,,,,
因为,所以,
所以,,,
设平面的法向量为,则即
令,则,,.
设平面的法向量为,则即
令,则,,.
所以二面角的余弦值为.
21.(1)答案不唯一,具体见解析;(2)证明见解析.
解:(1)由题得,其中,
考察,,
其中对称轴为,.
若,则,此时,
则,所以在上单调递增;
若,则,此时在上有两个根,
即,.
且,所以当时,,
则,单调递增;
当时,,则,单调递减;
当时,,则,单调递增,
综上,当时,在上单调递增;
当时,在上单调递增.
在上单调递减,在上单调递增.
(2)证明:由(1)知,当时,有两个极值点,
且,,
所以
.
令,,
由于,
故在上单调递增,所以.
所以,即.
22.(1);(2)是,.
(2)设,,,
当时,设直线,的方程分别为,,
由
,,,
,
,
,
,
同理由
.
.
当时,直线,与轴重合,
.
综上,.
试卷第1 11页,总2 22页
试卷第1 11页,总2 22页
理科数学试卷
一、选择题(每题5分,共60分)
1.已知复数满足 ,则的共轭复数对应的点位于复平面的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.若函数的图象在点处的切线方程是,则( )
A.1 B.2 C.3 D.4
3.计算定积分( )
A. B. C. D.
4.函数在定义域内可导,其图像如图所示.记的导函数为,则不等式的解集为( )
A. B.
C. D.
5.人口普查是世界各国所广泛采用的搜集人口资料的一种科学方法,是提供全国基本人口数据的主要来源.根据人口普查的基本情况,可以科学的研究制定社会、经济、科教等各项发展政策,是国家科学决策的重要基础工作,人口普查资料是制定人口政策的依据和前提.截止目前,我国共进行了七次人口普查,下图是这七次普查的全国人口及年均增长率情况,下列说法正确的是( )
A.年均增长率逐次减小
B.年均增长率的极差是1.08%
C.这七次普查的人口数逐次增加,且第四次增幅最小
D.第七次普查的人口数最多,且第三次增幅最大
6.某工厂利用随机数表对生产的50个零件进行抽样测试,先将50个零件进行编号,编号分别为01,02,…,50,从中抽取5个样本,下面提供随机数表的第1行到第2行:
若从表中第1行第9列开始向右依次读取数据,则得到的第4个样本编号是( )
A.10 B.09 C.71 D.20
7.某种碘是一种放射性物质,该碘最初一段时间衰减的时间(单位:分钟)与剩余量(单位:克)存在着较强的线性相关关系.如下表是某校化学社团师生观测该碘在5天内衰减情况得出的一组数据,则对的线性回归方程可以是( )
(单位:分钟) 10 20 30 40 50
(单位:克) 22.5 19 17.5 15 11
A. B.
C. D.
8.我国脱贫攻坚战取得了全面胜利,现行标准下农村贫困人口全部脱贫,贫困县全部摘帽,贫困村全部出列,区域性整体贫困得到解决,完成了消除绝对贫困的艰巨任务,创造了又一个彪炳史册的人间奇迹!脱贫攻坚取得胜利后,我国建立了防止返贫检测和帮扶机制,继续巩固脱贫成果.为进一步推进乡村振兴,某市扶贫办在A乡镇的3个脱贫村与B乡镇的4个脱贫村中,随机抽取两个村庄进一步实施产业帮扶,则抽取的两个脱贫村为同一乡镇的概率为( )
A. B. C. D.
9.已知的展开式中所有项的系数和为192,则展开式中的常数项为( )
A.8 B.6 C.4 D.2
10.执行如图所示的程序框图,则输出的结果为( )
A.5 B.4 C.3 D.2
11.函数图像的切线斜率为k,则的最小值为( )
A. B. C.1 D.2
12.若,则( )
A. B.
C. D.
二、填空题(每题5分,共20分)
13.函数的单调递增区间为___________.
14.,.通过观察上述两等式的共同规律,请你写出一个一般性的命题___________.
15.对某种电子元件使用寿命跟踪调查,所得样本频率分布直方图如图,若一批电子元件中寿命在100~300小时的电子元件的数量为400,则寿命在500~600小时的电子元件的数量为_______.
16.已知函数.
①曲线上存在垂直于y轴的切线;②函数有四个零点;
③函数有三个极值点; ④方程有四个根.
上述结论中正确的是_______________.
三、解答题(共70分)
17.(共10分)已知函数在时有极值为
(1)求实数的值;
(2)求当 时,的最大值.
18.(共12分)某农林科技大学培育出某一小麦新品种,为检验该新品种小麦的最佳播种日期,把一块地均分为,两块试验田(假设,两块试验田地质情况一致),10月10日在试验田播种该新品种小麦,10月20日在试验田播种该新品种小麦,小麦收割后,从这两块试验田收获的小麦中各随机抽取了20份(每份1000粒),并测其千粒重(单位:),按照[20,30),[30,40),[40,50]进行分组,得到如下表格.其中千粒重不低于的小麦视为饱满,否则为不饱满.
[20,30) [30,40) [40,50]
试验田/份 4 7 9
试验田/份 7 10 3
(1)完成下面的列联表,并判断是否有95%的把握认为小麦是否饱满与播种日期有关;
10月10日播种 10月20日播种 合计
饱满
不饱满
合计
(2)用样本估计总体,从试验田随机选取50份(每份1000粒)小麦,记饱满的小麦份数为,求数学期望.
参考公式:,其中.
() 0.15 0.10 0.05 0.025 0.010 0.001
2.072 2.706 3.841 5.024 6.635 10.828
19.(共12分)在平面直角坐标系中,直线的参数方程为(为参数).以坐标原点为极点,轴非负半轴为极轴建立极坐标系,圆的极坐标方程为.
(1)求圆的标准方程.
(2)直线与圆的相交弦为,是弦上动点,求 的取值范围.
20.(共12分)如图,多面体中,平面,底面为等腰梯形,,,,,且.
(1)求证:平面;
(2)求二面角的余弦值.
21.(共12分)已知函数,其中.
(1)讨论的单调性;
(2)若有两个极值点,证明.
22.(共12分)已知椭圆的离心率为,左、右焦点分别为,,上、
下顶点分别为,四边形的面积为 .
(1)求椭圆的标准方程;
(2)点是椭圆上一动点,直线,分别与椭圆交于点,,试问:是否为定值?若是,求出该定值.
哈尔滨市重点高中2019级高二下6月阶段检测
答案
1~12
;14.;15.300;16.①③④
17.(1);(2)最大值0.
解:(1)由可得
又为极值点,所以
又极值为,即,则
可得:或
当时,,
↗ 极大值 ↘ 极小值 ↗
当时,
所以在上单调递增,无极值,综上.
(2)由(1)知,,为增函数,时,为减函数,
最大值0
18.(1)填表见解析;有;(2).
(1)补全的列联表如下:
10月10日播种 10月20日播种 合计
饱满 9 3 12
不饱满 11 17 28
合计 20 20 40
由表中的数据可得,
由于,
所以有95%的把握认为小麦是否饱满与播种日期有关.
(2)因为从试验田的样本中随机抽取1份小麦,抽到饱满小麦的概率为,
所以,
故.
19.(1);(2).
(1)由得:,
化为直角坐标方程为:,
圆的标准方程为.
(2),,
由(1)知:圆的圆心为,半径,
则由参数的几何意义知:,解得:,
的取值范围为.
20.(1)证明见解析;(2).
(1)中,,.
设,连结,
,,.
,又,所以四边形为平行四边形,
,又平面,平面,
平面.
(2)由(1)知,,,
以,,分别为x,y,z轴建立空间直角坐标系,如图所示,
则,,,,
因为,所以,
所以,,,
设平面的法向量为,则即
令,则,,.
设平面的法向量为,则即
令,则,,.
所以二面角的余弦值为.
21.(1)答案不唯一,具体见解析;(2)证明见解析.
解:(1)由题得,其中,
考察,,
其中对称轴为,.
若,则,此时,
则,所以在上单调递增;
若,则,此时在上有两个根,
即,.
且,所以当时,,
则,单调递增;
当时,,则,单调递减;
当时,,则,单调递增,
综上,当时,在上单调递增;
当时,在上单调递增.
在上单调递减,在上单调递增.
(2)证明:由(1)知,当时,有两个极值点,
且,,
所以
.
令,,
由于,
故在上单调递增,所以.
所以,即.
22.(1);(2)是,.
(2)设,,,
当时,设直线,的方程分别为,,
由
,,,
,
,
,
,
同理由
.
.
当时,直线,与轴重合,
.
综上,.
试卷第1 11页,总2 22页
试卷第1 11页,总2 22页
同课章节目录
