第4章 一元一次不等式(组) 4.3 一元一次不等式的解法课件——八年级数学湘教版上册(共15张)
文档属性
| 名称 | 第4章 一元一次不等式(组) 4.3 一元一次不等式的解法课件——八年级数学湘教版上册(共15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 273.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 23:55:56 | ||
图片预览






文档简介
(共15张PPT)
4.3
第1课时 一元一次不等式的解法
第四章
一元一次不等式(组)
情景引入
本问题中涉及的数量关系是:
工人重+货物重≤最大载重量.
设能载x件25kg重的货物,因为升降机最大载重量是1200kg,所以有75+25x≤1200.①
PS:含有未知数的项的系数不能为0,且不等号左右两边都是整式
像75+25x≤1200这样,含有一个未知数,且含未知数的项的次数是1的不等式,称为一元一次不等式.
获取新知
①③
为了求出升降机能装载货物的件数,需要求出满足不等式75+25x≤1200的x的值.如何求呢?
与解一元一次方程类似,我们将根据不等式的基本性质,进行如下步骤:
将①式移项,得25x≤1200-75,
即25x≤1125.②
将②式两边都除以25(即将x的系数化为1),得x≤45.
因此,升降机最多装载45件25kg重的货物.
求一个不等式的解集的过程称为解不等式.
我们把满足一个不等式的未知数的每一个值,称为这个不等式的一个解.例如,5.4,6,7.8都是3x>15的解.这样的解有无数个.
我们把一个不等式的解的全体称为这个不等式的解集.
例如,我们用x>5表示3x>15的解集.
今后我们在解一元一次不等式时,将利用前面讲述的不等式的基本性质,将原不等式化成形如x≤a(或xa,x≥a)的不等式,就可得到原不等式的解集.
(1)x的2倍加1等于x的5倍加10
,求x.
(2)x的2倍加1不小于x的5倍加10
,求x.
解:(1)2x+1=5x+10
2x-5x=10-1
-3x=9
x=-3
(2)2x+1≥5x+10
2x-5x≥10-1
-3x≥9
x≤-3
通过比较这两题的练习,你对这两类题目的解法有什么印象?
解一元一次方程与解一元一次不等式的方法、步骤类似.
例题讲解
步骤
①
②
③
④
⑤
6-2(x-2)=3x
6-2x+4=3x
-2x-3x=-6-4
-5x=-10
x=2
6-2(x-2)>3x
6-2x+4>3x
-2x-3x>-6-4
-5x>-10
x<2
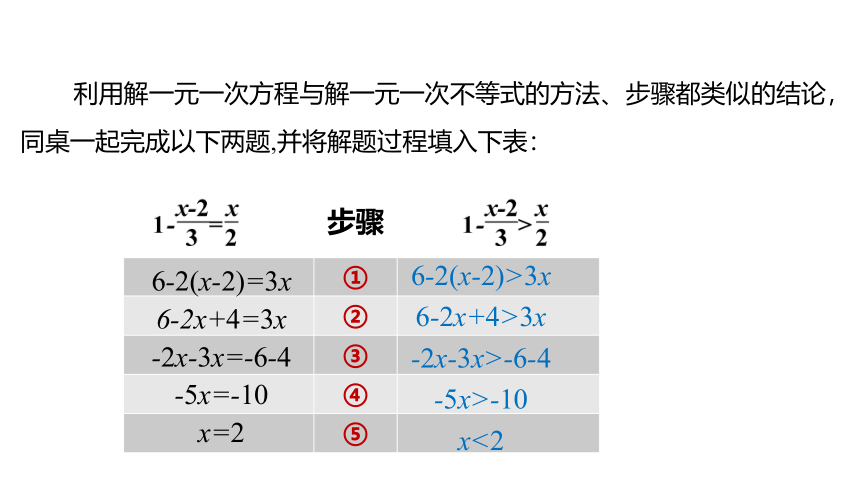
利用解一元一次方程与解一元一次不等式的方法、步骤都类似的结论,同桌一起完成以下两题,并将解题过程填入下表:
利用上表归纳解一元一次不等式的一般步骤,并指出每个步骤的根据,完成下表:
写不等式的解时,要把表示未知数的字母写在不等号的左边。
序号
步骤
根据
①
②
③
④
⑤
去分母
去括号
移项
合并同类项
两边同除以a
不等式的基本性质2,3
单项式乘以多项式法则
不等式的基本性质1
合并同类项法则
不等式的基本性质2,3
一元一次方程
一元一次不等式
解法步骤
解的情况
区别
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
方程的解法
不等式的解法
PK
一般只有一个解
一般解集含有无数个解
在(1)与(5)这两步若乘数(或除数)为负数,要把不等号方向改变
例1
解下列一元一次不等式
:
(1)
2-5x
<
8-6x
;
(2)
.
例题讲解
解
(1)
原不等式为2-5x
<
8-6x
将同类项放在一起
即,得
x
<
6
移项,得
-5x+6x
<
8-2
计算结果
解
首先将分母去掉
去括号,得
2x
-10
+
6
≤
9x
去分母,得
2(x
-5)+1×6
≤
9x
移项,得
2x
-
9x
≤
10
-
6
去括号
将同类项放在一起
(2)
原不等式为
合并同类项,得:
-7x
≤
4
两边都除以-7,得
x
≥
计算结果
根据不等式性质3
1.
解下列不等式:
(1)
-5x
≤
10
;
(2)4x
-3
<
10x
+
7
.
解
(1)
原不等式为
-5x
≤
10
方程两边同除以-5,
x
≥
-2
(2)
原不等式为
4x
-3
<
10x
+
7
移项,得
4x
-10x
<
3+7
化简,得
-6x
<
10
方程两边同除以
-6,
x
>
随堂演练
2.
解下列不等式:
(1)
3x
-1
>
2(2-5x)
;
(2)
.
解
(1)
原不等式为
3x
-1
>
2(2-5x)
去括号,得
3x-1
>
4-10x
移项,得
3x+10x
>
1+4
化简,得
13x
>
5
两边同除以13,
x
>
(2)
原不等式为
去分母,得
2(x+2)≥
3(2x-3)
去括号,得
2x+4
≥
6x-9
移项,得
2x
-6x
≥
-4-9
化简,得
-4x
≥
-13
两边同除以
-4,
x
≤
课堂小结
谢谢观看
4.3
第1课时 一元一次不等式的解法
第四章
一元一次不等式(组)
情景引入
本问题中涉及的数量关系是:
工人重+货物重≤最大载重量.
设能载x件25kg重的货物,因为升降机最大载重量是1200kg,所以有75+25x≤1200.①
PS:含有未知数的项的系数不能为0,且不等号左右两边都是整式
像75+25x≤1200这样,含有一个未知数,且含未知数的项的次数是1的不等式,称为一元一次不等式.
获取新知
①③
为了求出升降机能装载货物的件数,需要求出满足不等式75+25x≤1200的x的值.如何求呢?
与解一元一次方程类似,我们将根据不等式的基本性质,进行如下步骤:
将①式移项,得25x≤1200-75,
即25x≤1125.②
将②式两边都除以25(即将x的系数化为1),得x≤45.
因此,升降机最多装载45件25kg重的货物.
求一个不等式的解集的过程称为解不等式.
我们把满足一个不等式的未知数的每一个值,称为这个不等式的一个解.例如,5.4,6,7.8都是3x>15的解.这样的解有无数个.
我们把一个不等式的解的全体称为这个不等式的解集.
例如,我们用x>5表示3x>15的解集.
今后我们在解一元一次不等式时,将利用前面讲述的不等式的基本性质,将原不等式化成形如x≤a(或x
(1)x的2倍加1等于x的5倍加10
,求x.
(2)x的2倍加1不小于x的5倍加10
,求x.
解:(1)2x+1=5x+10
2x-5x=10-1
-3x=9
x=-3
(2)2x+1≥5x+10
2x-5x≥10-1
-3x≥9
x≤-3
通过比较这两题的练习,你对这两类题目的解法有什么印象?
解一元一次方程与解一元一次不等式的方法、步骤类似.
例题讲解
步骤
①
②
③
④
⑤
6-2(x-2)=3x
6-2x+4=3x
-2x-3x=-6-4
-5x=-10
x=2
6-2(x-2)>3x
6-2x+4>3x
-2x-3x>-6-4
-5x>-10
x<2
利用解一元一次方程与解一元一次不等式的方法、步骤都类似的结论,同桌一起完成以下两题,并将解题过程填入下表:
利用上表归纳解一元一次不等式的一般步骤,并指出每个步骤的根据,完成下表:
写不等式的解时,要把表示未知数的字母写在不等号的左边。
序号
步骤
根据
①
②
③
④
⑤
去分母
去括号
移项
合并同类项
两边同除以a
不等式的基本性质2,3
单项式乘以多项式法则
不等式的基本性质1
合并同类项法则
不等式的基本性质2,3
一元一次方程
一元一次不等式
解法步骤
解的情况
区别
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
方程的解法
不等式的解法
PK
一般只有一个解
一般解集含有无数个解
在(1)与(5)这两步若乘数(或除数)为负数,要把不等号方向改变
例1
解下列一元一次不等式
:
(1)
2-5x
<
8-6x
;
(2)
.
例题讲解
解
(1)
原不等式为2-5x
<
8-6x
将同类项放在一起
即,得
x
<
6
移项,得
-5x+6x
<
8-2
计算结果
解
首先将分母去掉
去括号,得
2x
-10
+
6
≤
9x
去分母,得
2(x
-5)+1×6
≤
9x
移项,得
2x
-
9x
≤
10
-
6
去括号
将同类项放在一起
(2)
原不等式为
合并同类项,得:
-7x
≤
4
两边都除以-7,得
x
≥
计算结果
根据不等式性质3
1.
解下列不等式:
(1)
-5x
≤
10
;
(2)4x
-3
<
10x
+
7
.
解
(1)
原不等式为
-5x
≤
10
方程两边同除以-5,
x
≥
-2
(2)
原不等式为
4x
-3
<
10x
+
7
移项,得
4x
-10x
<
3+7
化简,得
-6x
<
10
方程两边同除以
-6,
x
>
随堂演练
2.
解下列不等式:
(1)
3x
-1
>
2(2-5x)
;
(2)
.
解
(1)
原不等式为
3x
-1
>
2(2-5x)
去括号,得
3x-1
>
4-10x
移项,得
3x+10x
>
1+4
化简,得
13x
>
5
两边同除以13,
x
>
(2)
原不等式为
去分母,得
2(x+2)≥
3(2x-3)
去括号,得
2x+4
≥
6x-9
移项,得
2x
-6x
≥
-4-9
化简,得
-4x
≥
-13
两边同除以
-4,
x
≤
课堂小结
谢谢观看
同课章节目录
