6.2平面向量的运算第二课时-【新教材】人教A版(2019)高中数学必修第二册同步讲义(含答案)
文档属性
| 名称 | 6.2平面向量的运算第二课时-【新教材】人教A版(2019)高中数学必修第二册同步讲义(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 582.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 01:03:35 | ||
图片预览




文档简介
第六章 平面向量及其应用
6.2平面向量的运算
第2课时 向量的数乘运算
【课程标准】
通过实例分析,掌握平面向量的数乘运算及其运算规则,理解其几何意义。
了解平面向量的线性运算性及其几何意义。
掌握平面向量基本定理及其证明过程,会根据向量共线定理判断两个向量是否共线。
【知识要点归纳】
1.数乘向量
(1)定义:
一般地,给定一个实数λ与任意一个向量a,规定它们的乘积是一个向量,记作λa,其中:
①当λ≠0且a≠0时,λa的模为|λ||a|,而且λa的方向如下:
(i)当λ>0时,与a的方向相同;
(ii)当λ<0时,与a的方向相反.
②当λ=0或a=0时,λa=0.
上述实数λ与向量a相乘的运算简称为数乘向量.
(2)几何意义:把向量a沿着a的方向或a的反方向放大或缩小.
(3)运算律:
设λ,μ为实数,则
①(λ+μ)a=λ a+μ a;
②λ(μ a)=(λμ)a;
③λ(a+b)=λa+λb.
注意:数乘向量与实数的乘法的区别。
[提示] (1)数乘向量与实数的乘法是有区别的,前者的结果是一个向量,后者的结果是一个实数.特别要注意λ=0时,λa=0,此处最容易出现的错误是将实数0与0混淆,错误地表述成λa=0.
(2)要注意实数与向量可以求积,但是不能进行加减运算,如λ+a,λ-a是无法运算的.
2.线性运算:向量的加、减、数乘运算统称为向量的线性运算,向量线性运算的结果仍是向量.对于任意向量a,b,以及任意实数λ,μ1,μ2,恒有λ(μ1a+μ2b)=λμ1a±λμ2b.
3.共线向量定理
向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ,使b=λa.
【经典例题】
例1.已知false,false,
(1)求false.
(2)求false。
例2.已知false,false,false,false都是向量,且false,false,试用false,false分别表示false,false.
例3.已知两个非零向量false与false不共线,false,false,false.
(1)若false,求false的值;
(2)若false,false,false三点共线,求false的值.
例4.已知非零向量false,false,false,false,false,求证:false,false,false三点在同一条直线上.
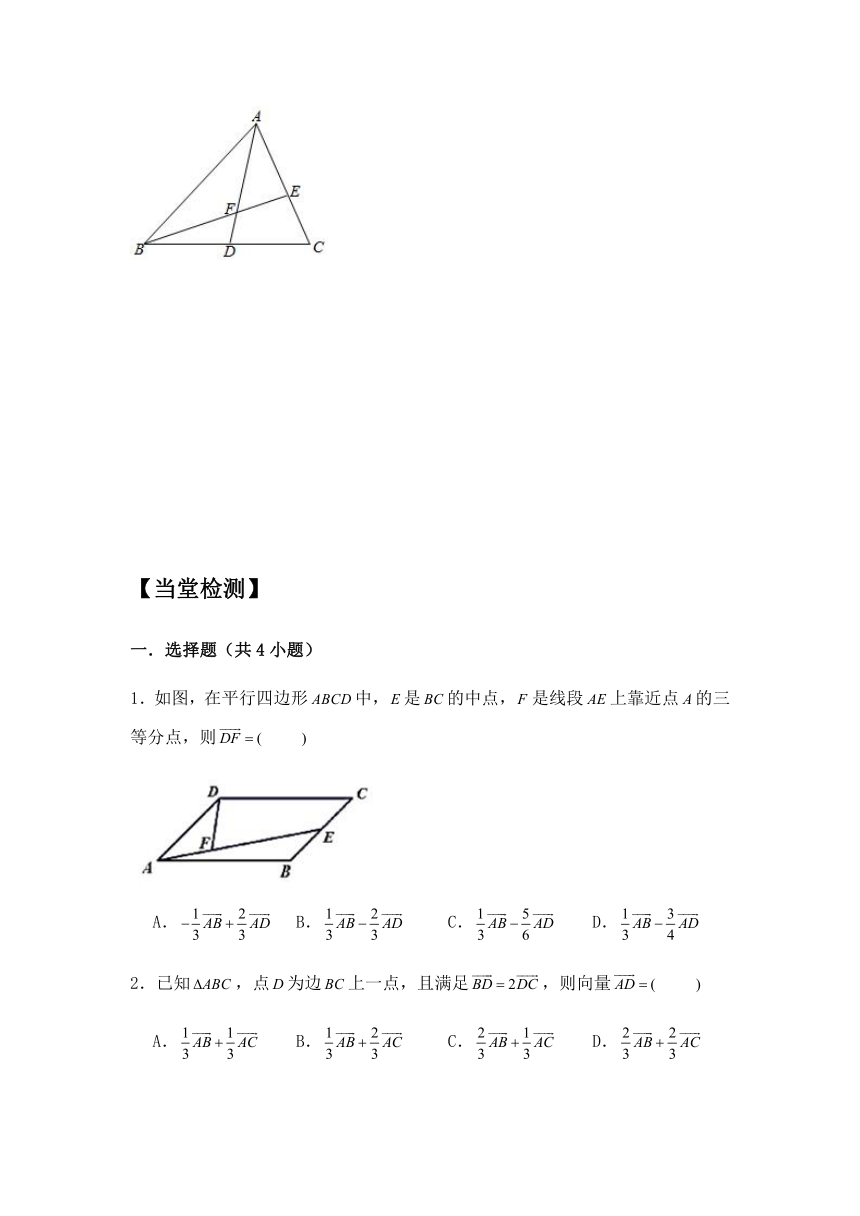
例5.如图,已知false中,false为false的中点,false,false,false交于点false,设false,false.
(1)用false,false分别表示向量false,false;
(2)若false,求实数false的值.
【当堂检测】
一.选择题(共4小题)
1.如图,在平行四边形false中,false是false的中点,false是线段false上靠近点false的三等分点,则false false
A.false B.false C.false D.false
2.已知false,点false为边false上一点,且满足false,则向量false false
A.false B.false C.false D.false
3.在平行四边形false中,false为false的中点,false为false的中点,则false false
A.false B.false C.false D.false
4.在false所在的平面上有一点false,满足false,设false,false,则false false
A.false B.false C.false D.false
二.填空题(共2小题)
5.在false中,点false,false分别在边false,false上,且false,false,记false,false,若false,则false的值为 .
6.在平行四边形false中,false,则false (用false表示).
三.解答题(共1小题)
7.已知平行四边形false中,若false是该平面上任意一点,则满足false.
(1)若false是false的中点,求false的值;
(2)若false、false、false三点共线,求证:false.
当堂检测答案
一.选择题(共4小题)
1.如图,在平行四边形false中,false是false的中点,false是线段false上靠近点false的三等分点,则false false
A.false B.false C.false D.false
【分析】利用平面向量的基本定理,用false和false线性表示false向量即可.
【解答】解:由可知,false,
故选:false.
【点评】本题主要考查了平面向量的基本定理,以及向量的线性表示,是基础题.
2.已知false,点false为边false上一点,且满足false,则向量false false
A.false B.false C.false D.false
【分析】根据false可得出false,然后进行向量的数乘运算求出false即可.
【解答】解:falsefalse,
falsefalse,
falsefalse.
故选:false.
【点评】本题考查了向量减法的几何意义,向量的数乘运算,考查了计算能力,属于基础题.
3.在平行四边形false中,false为false的中点,false为false的中点,则false false
A.false B.false C.false D.false
【分析】根据条件可画出图形,根据向量加法、减法和数乘的几何意义即可用false表示出向量false.
【解答】解:如图,false四边形false为平行四边形,false为false的中点,false为false的中点,
falsefalse
false
false
false
false.
故选:false.
【点评】本题考查了向量加法、减法和数乘的几何意义,向量的数乘运算,考查了计算能力,属于基础题.
4.在false所在的平面上有一点false,满足false,设false,false,则false false
A.false B.false C.false D.false
【分析】由向量加减的三角形法则结合相反向量的定义,可得false为线段false的一个三等分点,再根据向量的加减的几何意义即可求出答案.
【解答】解:falsefalse,
falsefalse;
即false;
故点false是false边上的第二个三等分点;
false;
故选:false.
【点评】本题考查向量的运算法则,涉及共线向量定理,属基础题.
二.填空题(共2小题)
5.在false中,点false,false分别在边false,false上,且false,false,记false,false,若false,则false的值为 false .
【分析】可画出图形,根据false,false即可得出false,再根据false便可得出false,又知false,这样根据平面向量基本即可求出false,false的值.
【解答】解:如图,
false,false;
falsefalse,false,且false;
falsefalse;
又false;
false根据平面向量基本定理得,false;
falsefalse.
故答案为:false.
【点评】考查向量加法、减法和数乘的几何意义,以及向量的数乘运算,平面向量基本定理.
6.在平行四边形false中,false,则false false (用false表示).
【分析】根据向量的线性运算性质及几何意义,由false得false,利用向量的三角形法则得false,且false,最后将左式的两个向量都用用false表示即得.
【解答】解:由false得false,且false,
又false,
falsefalse.
故答案为:false.
【点评】本题考点是向量加减混合运算及其几何意义,考查了向量加法与减法法则,解题的关键是熟练掌握向量加减法的法则,根据图象将所研究的向量用基向量表示出来,本题考查数形结合的思想,是向量在几何中运用的基础题型.
三.解答题(共1小题)
7.已知平行四边形false中,若false是该平面上任意一点,则满足false.
(1)若false是false的中点,求false的值;
(2)若false、false、false三点共线,求证:false.
【分析】(1)false是false的中点时,可得出false,从而根据平面向量基本定理得出false;
(2)根据false,false,false三点共线可得出false与false共线,从而得出false,进而得出false,这样根据平面向量基本定理即可得出false.
【解答】解:(1)若false是false的中点,则false,
又false,
false根据平面向量基本定理得,false,
falsefalse;
(2)证明:false,false,false三点共线,
falsefalse和false共线,
false存在实数false,使false,
falsefalse,
falsefalse,
又false,
false根据平面向量基本定理得,false.
【点评】本题考查了向量加法的平行四边形法则,共线向量和平面向量基本定理,以及向量减法的几何意义,向量的数乘运算,考查了计算和推理能力,属于基础题.
6.2平面向量的运算
第2课时 向量的数乘运算
【课程标准】
通过实例分析,掌握平面向量的数乘运算及其运算规则,理解其几何意义。
了解平面向量的线性运算性及其几何意义。
掌握平面向量基本定理及其证明过程,会根据向量共线定理判断两个向量是否共线。
【知识要点归纳】
1.数乘向量
(1)定义:
一般地,给定一个实数λ与任意一个向量a,规定它们的乘积是一个向量,记作λa,其中:
①当λ≠0且a≠0时,λa的模为|λ||a|,而且λa的方向如下:
(i)当λ>0时,与a的方向相同;
(ii)当λ<0时,与a的方向相反.
②当λ=0或a=0时,λa=0.
上述实数λ与向量a相乘的运算简称为数乘向量.
(2)几何意义:把向量a沿着a的方向或a的反方向放大或缩小.
(3)运算律:
设λ,μ为实数,则
①(λ+μ)a=λ a+μ a;
②λ(μ a)=(λμ)a;
③λ(a+b)=λa+λb.
注意:数乘向量与实数的乘法的区别。
[提示] (1)数乘向量与实数的乘法是有区别的,前者的结果是一个向量,后者的结果是一个实数.特别要注意λ=0时,λa=0,此处最容易出现的错误是将实数0与0混淆,错误地表述成λa=0.
(2)要注意实数与向量可以求积,但是不能进行加减运算,如λ+a,λ-a是无法运算的.
2.线性运算:向量的加、减、数乘运算统称为向量的线性运算,向量线性运算的结果仍是向量.对于任意向量a,b,以及任意实数λ,μ1,μ2,恒有λ(μ1a+μ2b)=λμ1a±λμ2b.
3.共线向量定理
向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ,使b=λa.
【经典例题】
例1.已知false,false,
(1)求false.
(2)求false。
例2.已知false,false,false,false都是向量,且false,false,试用false,false分别表示false,false.
例3.已知两个非零向量false与false不共线,false,false,false.
(1)若false,求false的值;
(2)若false,false,false三点共线,求false的值.
例4.已知非零向量false,false,false,false,false,求证:false,false,false三点在同一条直线上.
例5.如图,已知false中,false为false的中点,false,false,false交于点false,设false,false.
(1)用false,false分别表示向量false,false;
(2)若false,求实数false的值.
【当堂检测】
一.选择题(共4小题)
1.如图,在平行四边形false中,false是false的中点,false是线段false上靠近点false的三等分点,则false false
A.false B.false C.false D.false
2.已知false,点false为边false上一点,且满足false,则向量false false
A.false B.false C.false D.false
3.在平行四边形false中,false为false的中点,false为false的中点,则false false
A.false B.false C.false D.false
4.在false所在的平面上有一点false,满足false,设false,false,则false false
A.false B.false C.false D.false
二.填空题(共2小题)
5.在false中,点false,false分别在边false,false上,且false,false,记false,false,若false,则false的值为 .
6.在平行四边形false中,false,则false (用false表示).
三.解答题(共1小题)
7.已知平行四边形false中,若false是该平面上任意一点,则满足false.
(1)若false是false的中点,求false的值;
(2)若false、false、false三点共线,求证:false.
当堂检测答案
一.选择题(共4小题)
1.如图,在平行四边形false中,false是false的中点,false是线段false上靠近点false的三等分点,则false false
A.false B.false C.false D.false
【分析】利用平面向量的基本定理,用false和false线性表示false向量即可.
【解答】解:由可知,false,
故选:false.
【点评】本题主要考查了平面向量的基本定理,以及向量的线性表示,是基础题.
2.已知false,点false为边false上一点,且满足false,则向量false false
A.false B.false C.false D.false
【分析】根据false可得出false,然后进行向量的数乘运算求出false即可.
【解答】解:falsefalse,
falsefalse,
falsefalse.
故选:false.
【点评】本题考查了向量减法的几何意义,向量的数乘运算,考查了计算能力,属于基础题.
3.在平行四边形false中,false为false的中点,false为false的中点,则false false
A.false B.false C.false D.false
【分析】根据条件可画出图形,根据向量加法、减法和数乘的几何意义即可用false表示出向量false.
【解答】解:如图,false四边形false为平行四边形,false为false的中点,false为false的中点,
falsefalse
false
false
false
false.
故选:false.
【点评】本题考查了向量加法、减法和数乘的几何意义,向量的数乘运算,考查了计算能力,属于基础题.
4.在false所在的平面上有一点false,满足false,设false,false,则false false
A.false B.false C.false D.false
【分析】由向量加减的三角形法则结合相反向量的定义,可得false为线段false的一个三等分点,再根据向量的加减的几何意义即可求出答案.
【解答】解:falsefalse,
falsefalse;
即false;
故点false是false边上的第二个三等分点;
false;
故选:false.
【点评】本题考查向量的运算法则,涉及共线向量定理,属基础题.
二.填空题(共2小题)
5.在false中,点false,false分别在边false,false上,且false,false,记false,false,若false,则false的值为 false .
【分析】可画出图形,根据false,false即可得出false,再根据false便可得出false,又知false,这样根据平面向量基本即可求出false,false的值.
【解答】解:如图,
false,false;
falsefalse,false,且false;
falsefalse;
又false;
false根据平面向量基本定理得,false;
falsefalse.
故答案为:false.
【点评】考查向量加法、减法和数乘的几何意义,以及向量的数乘运算,平面向量基本定理.
6.在平行四边形false中,false,则false false (用false表示).
【分析】根据向量的线性运算性质及几何意义,由false得false,利用向量的三角形法则得false,且false,最后将左式的两个向量都用用false表示即得.
【解答】解:由false得false,且false,
又false,
falsefalse.
故答案为:false.
【点评】本题考点是向量加减混合运算及其几何意义,考查了向量加法与减法法则,解题的关键是熟练掌握向量加减法的法则,根据图象将所研究的向量用基向量表示出来,本题考查数形结合的思想,是向量在几何中运用的基础题型.
三.解答题(共1小题)
7.已知平行四边形false中,若false是该平面上任意一点,则满足false.
(1)若false是false的中点,求false的值;
(2)若false、false、false三点共线,求证:false.
【分析】(1)false是false的中点时,可得出false,从而根据平面向量基本定理得出false;
(2)根据false,false,false三点共线可得出false与false共线,从而得出false,进而得出false,这样根据平面向量基本定理即可得出false.
【解答】解:(1)若false是false的中点,则false,
又false,
false根据平面向量基本定理得,false,
falsefalse;
(2)证明:false,false,false三点共线,
falsefalse和false共线,
false存在实数false,使false,
falsefalse,
falsefalse,
又false,
false根据平面向量基本定理得,false.
【点评】本题考查了向量加法的平行四边形法则,共线向量和平面向量基本定理,以及向量减法的几何意义,向量的数乘运算,考查了计算和推理能力,属于基础题.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
