1.3.2由三视图还原成实物图-北师大版高中数学必修二基础练习(Word含答案解析)
文档属性
| 名称 | 1.3.2由三视图还原成实物图-北师大版高中数学必修二基础练习(Word含答案解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 546.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 00:00:00 | ||
图片预览

文档简介
1.3.2由三视图还原成实物图
一、单选题
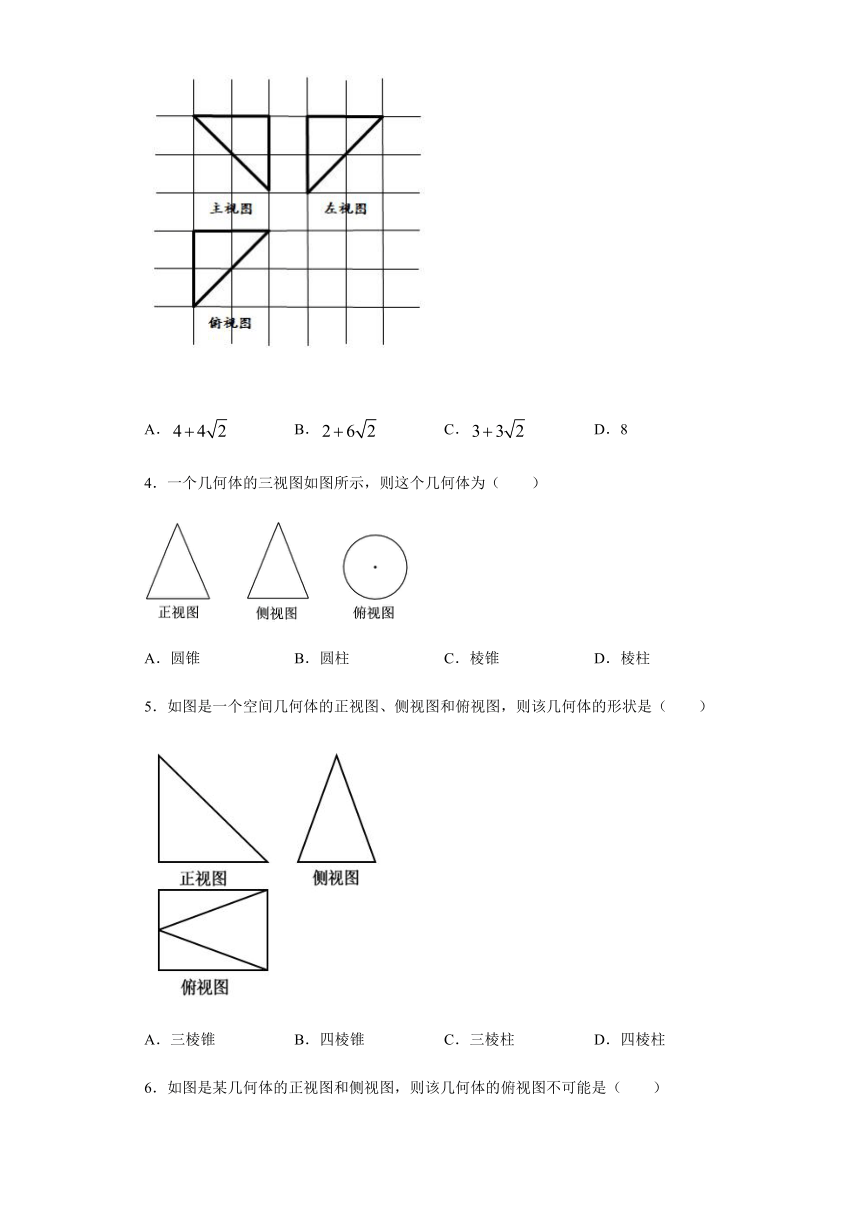
1.如图(1)(2)(3)(4)是四个几何体的三视图,这四个几何体依次分别是( )
A.三棱台.三棱柱.圆锥.圆台 B.三棱台.三棱锥.圆锥.圆台
C.三棱柱.四棱锥.圆锥.圆台 D.三棱柱.三棱台.圆锥.圆台
2.如图是一个物体的三视图,则此三视图所描述物体的直观图是( )
A. B. C. D.
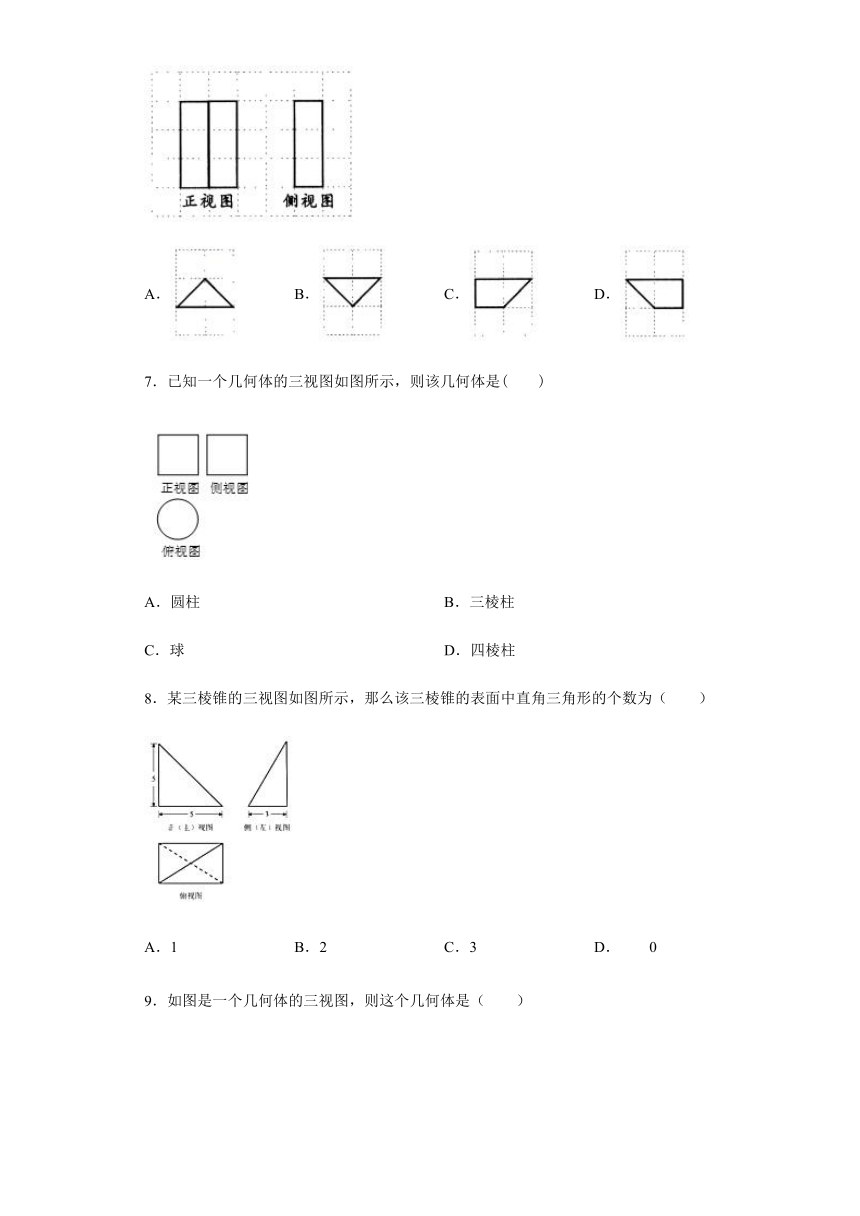
3.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的表面积为( )
A. B. C. D.8
4.一个几何体的三视图如图所示,则这个几何体为( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
5.如图是一个空间几何体的正视图、侧视图和俯视图,则该几何体的形状是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.四棱柱
6.如图是某几何体的正视图和侧视图,则该几何体的俯视图不可能是( )
A. B. C. D.
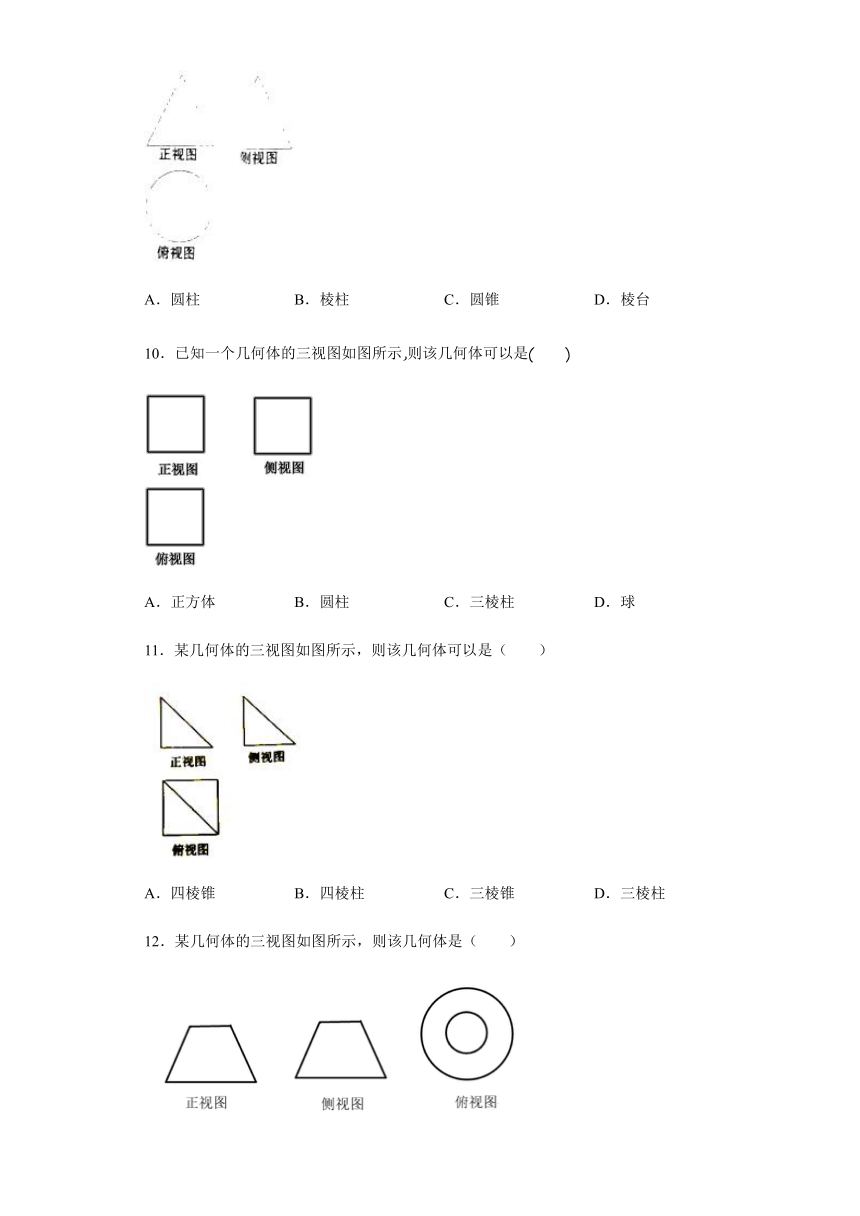
7.已知一个几何体的三视图如图所示,则该几何体是( )
A.圆柱 B.三棱柱
C.球 D.四棱柱
8.某三棱锥的三视图如图所示,那么该三棱锥的表面中直角三角形的个数为( )
A.1 B.2 C.3 D.0
9.如图是一个几何体的三视图,则这个几何体是( )
A.圆柱 B.棱柱 C.圆锥 D.棱台
10.已知一个几何体的三视图如图所示,则该几何体可以是( )
A.正方体 B.圆柱 C.三棱柱 D.球
11.某几何体的三视图如图所示,则该几何体可以是( )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
12.某几何体的三视图如图所示,则该几何体是( )
A.圆柱 B.圆锥 C.棱台 D.圆台
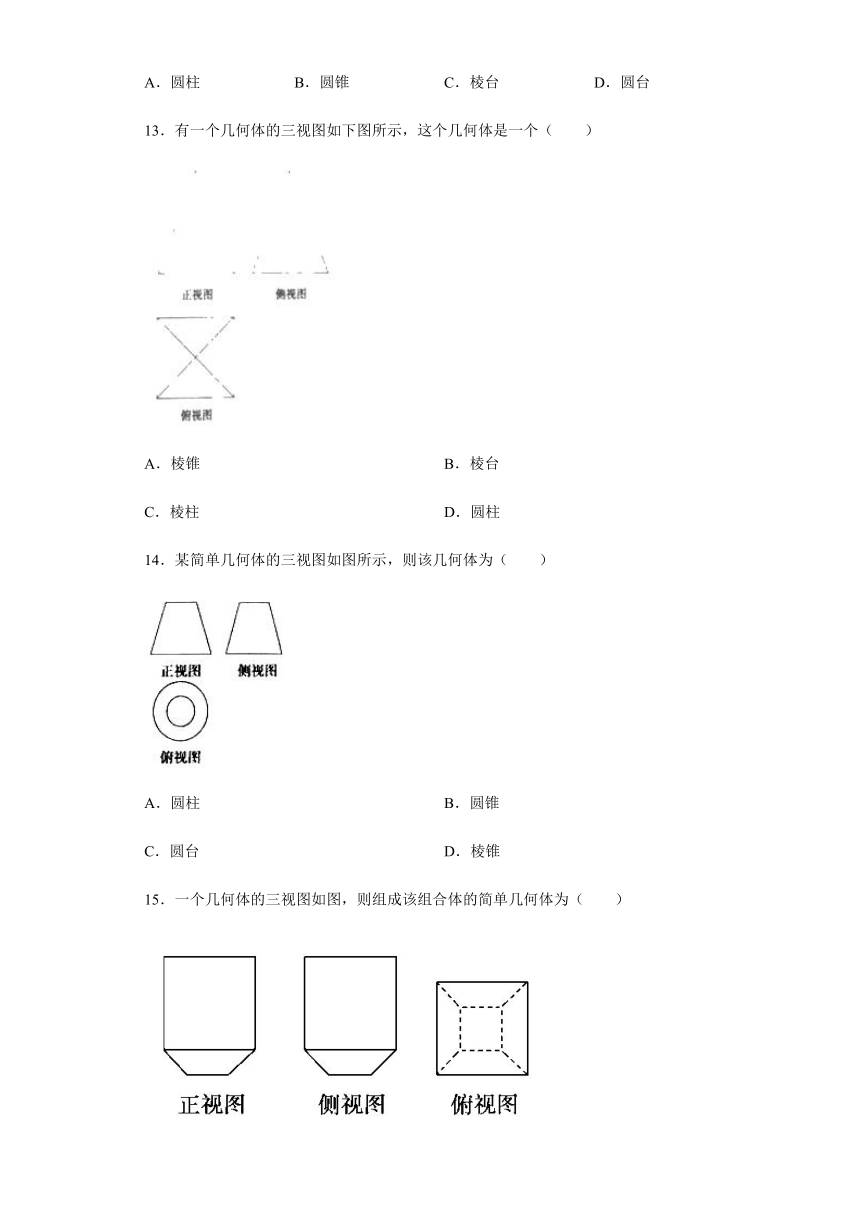
13.有一个几何体的三视图如下图所示,这个几何体是一个( )
A.棱锥 B.棱台
C.棱柱 D.圆柱
14.某简单几何体的三视图如图所示,则该几何体为( )
A.圆柱 B.圆锥
C.圆台 D.棱锥
15.一个几何体的三视图如图,则组成该组合体的简单几何体为( )
A.圆柱与圆台 B.四棱柱与四棱台 C.圆柱与四棱台 D.四棱柱与圆台
16.某几何体的三视图如图所示,那么这个几何体是( )
A.三棱锥 B.四棱锥 C.四棱台 D.三棱台
参考答案
1.C
【分析】
根据台体、锥体、柱体的三视图的特征进行判断即可.
【详解】
(1)由三视图可知:该几何体是倒放的三棱柱;
(2)由三视图可知:该几何体是四棱锥;
(3)由三视图可知:该几何体是圆锥;
(4)由三视图可知:该几何体是圆台,
故选:C
2.D
【分析】
由圆柱、圆锥、圆台的三视图确定几何体形状.
【详解】
由三视图知原组合体上面是一个圆锥,下面是一个圆柱,只有D相符.
故选:D.
3.A
【分析】
由三视图还原棱锥的直观图,即可求棱锥的表面积.
【详解】
由已知三视图,可得:此棱锥的直观图如下图所示:
和都是直角边为2和的直角三角形,
和均是腰长为2的等腰直角三角形,
所以其表面积为.
故选:A.
【点睛】
本题考查了根据三视图求几何体的表面积,空间想象能力,属于基础题.
4.A
【分析】
根据三视图可直接得到答案.
【详解】
根据三视图可得,该几何体为圆锥.
故选:A
【点睛】
本题考查的是由三视图还原几何体,较简单.
5.B
【分析】
根据棱柱、棱锥的特征判断.
【详解】
对照四个选项,棱柱的三视图最多只有一个三角形,而题中有两个视图是三角形,因此几何体是棱锥,在两个视图为三角形的情况下,第三个视图是四边形,因此原几何体是四棱锥.
故选:B.
【点睛】
本题考查三视图,考查基本几何体的三视图,掌握柱、锥、台、球的三视图的特征是解题关键.
6.A
【分析】
直接利用三视图和直观图的转换的应用求出结果.
【详解】
解:根据几何体的三视图可知该几何体为三棱柱,
当选A时,正视的中间的竖线应为虚线,选项BCD均可能,
故选:A
【点睛】
此题考查三视图与几何体之间的转换,考查学生的转换能力和空间想象能力,属于基础题.
7.A
【分析】
由三视图可直接得出答案.
【详解】
由三视图可知该几何体是圆柱
故选:A
【点睛】
本题考查的是三视图,较简单.
8.C
【分析】
由三视图还原原几何体,借助于正方体可得三棱锥的表面中直角三角形的个数.
【详解】
由三视图还原原几何体如图,
其中,,为直角三角形.
∴该三棱锥的表面中直角三角形的个数为3.
故选:C.
【点睛】
本小题主要考查由三视图还原为原图,属于基础题.
9.C
【分析】
由三视图的知识和三视图的形状直接判断即可得出答案.
【详解】
由主视图和侧视图都是三角形,俯视图为圆形,可得这个几何体为圆锥.
故选:C.
【点睛】
本题考查了三视图的识别,由三视图还原几何体,属于基础题.
10.A
【解析】
【分析】
主视图?左视图?俯视图是分别从物体正面?左面和上面看所得到的图形,即可求得答案.
【详解】
主视图?左视图?俯视图都是正方形
该几何体为正方体
故选:A.
【点睛】
本题主要考查了根据三视图判断其立体图形,解题关键是掌握三视图的基础知识,考查了分析能力和空间想象能力,属于基础题.
11.A
【分析】
直接根据三视图可以得到答案.
【详解】
根据俯视图为正方形,正视图和侧视图为直角三角形.
所以该几何体为四棱锥
故选:A
【点睛】
本题考查根据三视图分析原几何体的形状,属于基础题.
12.D
【分析】
根据简单几何体(柱、锥、台、球)的三视图确定.
【详解】
由柱、锥、台、球的三视图知题中三视图是圆台的三视图.
故选:D.
【点睛】
本题考查三视图,掌握基本几何体的三视图是解题基础.
13.A
【解析】
【分析】
根据三视图的特征可得这是一个锥体.
【详解】
根据三视图,正视图和侧视图是三角形,
所以这个几何体是一个棱锥.
故选:A
【点睛】
此题考查三视图的辨析,关键在于根据三视图的特征准确认识几何体的特征,需要在平常的学习中熟练掌握常见几何体的三视图特征.
14.C
【解析】
【分析】
由几何体的三视图可得则该几何体为圆台,得解.
【详解】
解:由正视图和侧视图可知,该几何体不可能是圆柱,即选项A错误,
由俯视图可知,该几何体不可能是棱锥、圆锥,即选项B、D错误,
因此该几何体为圆台,即选项C正确,
故选:C.
【点睛】
本题考查了空间几何体的三视图,属基础题.
15.B
【分析】
根据三视图的基本性质直接读取即可得出答案.
【详解】
由三视图可知该几何体是由两个基本体组合成的组合体,由上面部分的三视图可得上面基本体是四棱柱,由下面部分的三视图可得下面基本体是四棱台.故组成该组合体的简单几何体为四棱柱和四棱台.
故选:B.
【点睛】
本题考查了空间几何体三视图的识别与判断,熟练掌握常见空间几何体的三视图是解题的关键,属于基础题.
16.A
【解析】
【分析】
由正视图、侧视图可确定几何体为椎体;根据俯视图为三角形可知椎体为三棱锥.
【详解】
正视图和侧视图均为三角形 几何体为椎体
俯视图为三角形 该几何体为三棱锥
故选:
【点睛】
本题考查根据三视图还原几何体,属于基础题.
一、单选题
1.如图(1)(2)(3)(4)是四个几何体的三视图,这四个几何体依次分别是( )
A.三棱台.三棱柱.圆锥.圆台 B.三棱台.三棱锥.圆锥.圆台
C.三棱柱.四棱锥.圆锥.圆台 D.三棱柱.三棱台.圆锥.圆台
2.如图是一个物体的三视图,则此三视图所描述物体的直观图是( )
A. B. C. D.
3.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的表面积为( )
A. B. C. D.8
4.一个几何体的三视图如图所示,则这个几何体为( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
5.如图是一个空间几何体的正视图、侧视图和俯视图,则该几何体的形状是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.四棱柱
6.如图是某几何体的正视图和侧视图,则该几何体的俯视图不可能是( )
A. B. C. D.
7.已知一个几何体的三视图如图所示,则该几何体是( )
A.圆柱 B.三棱柱
C.球 D.四棱柱
8.某三棱锥的三视图如图所示,那么该三棱锥的表面中直角三角形的个数为( )
A.1 B.2 C.3 D.0
9.如图是一个几何体的三视图,则这个几何体是( )
A.圆柱 B.棱柱 C.圆锥 D.棱台
10.已知一个几何体的三视图如图所示,则该几何体可以是( )
A.正方体 B.圆柱 C.三棱柱 D.球
11.某几何体的三视图如图所示,则该几何体可以是( )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
12.某几何体的三视图如图所示,则该几何体是( )
A.圆柱 B.圆锥 C.棱台 D.圆台
13.有一个几何体的三视图如下图所示,这个几何体是一个( )
A.棱锥 B.棱台
C.棱柱 D.圆柱
14.某简单几何体的三视图如图所示,则该几何体为( )
A.圆柱 B.圆锥
C.圆台 D.棱锥
15.一个几何体的三视图如图,则组成该组合体的简单几何体为( )
A.圆柱与圆台 B.四棱柱与四棱台 C.圆柱与四棱台 D.四棱柱与圆台
16.某几何体的三视图如图所示,那么这个几何体是( )
A.三棱锥 B.四棱锥 C.四棱台 D.三棱台
参考答案
1.C
【分析】
根据台体、锥体、柱体的三视图的特征进行判断即可.
【详解】
(1)由三视图可知:该几何体是倒放的三棱柱;
(2)由三视图可知:该几何体是四棱锥;
(3)由三视图可知:该几何体是圆锥;
(4)由三视图可知:该几何体是圆台,
故选:C
2.D
【分析】
由圆柱、圆锥、圆台的三视图确定几何体形状.
【详解】
由三视图知原组合体上面是一个圆锥,下面是一个圆柱,只有D相符.
故选:D.
3.A
【分析】
由三视图还原棱锥的直观图,即可求棱锥的表面积.
【详解】
由已知三视图,可得:此棱锥的直观图如下图所示:
和都是直角边为2和的直角三角形,
和均是腰长为2的等腰直角三角形,
所以其表面积为.
故选:A.
【点睛】
本题考查了根据三视图求几何体的表面积,空间想象能力,属于基础题.
4.A
【分析】
根据三视图可直接得到答案.
【详解】
根据三视图可得,该几何体为圆锥.
故选:A
【点睛】
本题考查的是由三视图还原几何体,较简单.
5.B
【分析】
根据棱柱、棱锥的特征判断.
【详解】
对照四个选项,棱柱的三视图最多只有一个三角形,而题中有两个视图是三角形,因此几何体是棱锥,在两个视图为三角形的情况下,第三个视图是四边形,因此原几何体是四棱锥.
故选:B.
【点睛】
本题考查三视图,考查基本几何体的三视图,掌握柱、锥、台、球的三视图的特征是解题关键.
6.A
【分析】
直接利用三视图和直观图的转换的应用求出结果.
【详解】
解:根据几何体的三视图可知该几何体为三棱柱,
当选A时,正视的中间的竖线应为虚线,选项BCD均可能,
故选:A
【点睛】
此题考查三视图与几何体之间的转换,考查学生的转换能力和空间想象能力,属于基础题.
7.A
【分析】
由三视图可直接得出答案.
【详解】
由三视图可知该几何体是圆柱
故选:A
【点睛】
本题考查的是三视图,较简单.
8.C
【分析】
由三视图还原原几何体,借助于正方体可得三棱锥的表面中直角三角形的个数.
【详解】
由三视图还原原几何体如图,
其中,,为直角三角形.
∴该三棱锥的表面中直角三角形的个数为3.
故选:C.
【点睛】
本小题主要考查由三视图还原为原图,属于基础题.
9.C
【分析】
由三视图的知识和三视图的形状直接判断即可得出答案.
【详解】
由主视图和侧视图都是三角形,俯视图为圆形,可得这个几何体为圆锥.
故选:C.
【点睛】
本题考查了三视图的识别,由三视图还原几何体,属于基础题.
10.A
【解析】
【分析】
主视图?左视图?俯视图是分别从物体正面?左面和上面看所得到的图形,即可求得答案.
【详解】
主视图?左视图?俯视图都是正方形
该几何体为正方体
故选:A.
【点睛】
本题主要考查了根据三视图判断其立体图形,解题关键是掌握三视图的基础知识,考查了分析能力和空间想象能力,属于基础题.
11.A
【分析】
直接根据三视图可以得到答案.
【详解】
根据俯视图为正方形,正视图和侧视图为直角三角形.
所以该几何体为四棱锥
故选:A
【点睛】
本题考查根据三视图分析原几何体的形状,属于基础题.
12.D
【分析】
根据简单几何体(柱、锥、台、球)的三视图确定.
【详解】
由柱、锥、台、球的三视图知题中三视图是圆台的三视图.
故选:D.
【点睛】
本题考查三视图,掌握基本几何体的三视图是解题基础.
13.A
【解析】
【分析】
根据三视图的特征可得这是一个锥体.
【详解】
根据三视图,正视图和侧视图是三角形,
所以这个几何体是一个棱锥.
故选:A
【点睛】
此题考查三视图的辨析,关键在于根据三视图的特征准确认识几何体的特征,需要在平常的学习中熟练掌握常见几何体的三视图特征.
14.C
【解析】
【分析】
由几何体的三视图可得则该几何体为圆台,得解.
【详解】
解:由正视图和侧视图可知,该几何体不可能是圆柱,即选项A错误,
由俯视图可知,该几何体不可能是棱锥、圆锥,即选项B、D错误,
因此该几何体为圆台,即选项C正确,
故选:C.
【点睛】
本题考查了空间几何体的三视图,属基础题.
15.B
【分析】
根据三视图的基本性质直接读取即可得出答案.
【详解】
由三视图可知该几何体是由两个基本体组合成的组合体,由上面部分的三视图可得上面基本体是四棱柱,由下面部分的三视图可得下面基本体是四棱台.故组成该组合体的简单几何体为四棱柱和四棱台.
故选:B.
【点睛】
本题考查了空间几何体三视图的识别与判断,熟练掌握常见空间几何体的三视图是解题的关键,属于基础题.
16.A
【解析】
【分析】
由正视图、侧视图可确定几何体为椎体;根据俯视图为三角形可知椎体为三棱锥.
【详解】
正视图和侧视图均为三角形 几何体为椎体
俯视图为三角形 该几何体为三棱锥
故选:
【点睛】
本题考查根据三视图还原几何体,属于基础题.
