1.4空间图形的基本关系与公理-北师大版高中数学必修二基础练习(Word含答案解析)
文档属性
| 名称 | 1.4空间图形的基本关系与公理-北师大版高中数学必修二基础练习(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 844.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 15:04:52 | ||
图片预览




文档简介
1.4空间图形的基本关系与公理基础练习题
单选题
1.平面与平面平行,且直线,下列命题中正确的是( )
A.与内的所有直线垂直 B.与内的所有直线异面
C.与内的所有直线平行 D.与内的无数条直线平行
2.已知下列四个结论:①铺得很平的一张白纸是一个平面;②平面的形状是平行四边形;③一个平面的面积可以等于.其中正确结论的个数是( )
A. B. C. D.
3.如图所示的是平行四边形所在的平面,有下列表示方法:①平面;②平面;③平面;④平面;⑤;⑥平面.其中不正确的是( )
A.④⑤ B.③④⑤ C.②③④⑤ D.③⑤
4.下列叙述错误的是( )
A.若p∈α∩β,且α∩β=l,则p∈l.
B.若直线a∩b=A,则直线a与b能确定一个平面.
C.三点A,B,C确定一个平面.
D.若A∈l,B∈l且A∈α,B∈α则lα.
5.在空间中,下列结论正确的是( )
A.三角形确定一个平面 B.四边形确定一个平面
C.一个点和一条直线确定一个平面 D.两条直线确定一个平面
6.如图所示,用符号语言可表达为
A.,, B.,,
C.,,, D.,,,
7.两个平面若有三个公共点,则这两个平面( )
A.相交 B.重合
C.相交或重合 D.以上都不对
8.下面四个说法中,正确说法的个数为( )
(1)如果两个平面有三个公共点,那么这两个平面重合;
(2)两条直线可以确定一个平面;
(3)若,,,则;
(4)空间中,两两相交的三条直线在同一平面内.
A.1 B.2 C.3 D.4
9.四个顶点不在同一平面上的四边形中,,,,分别是边,,,上的点,如果直线,交于点,那么( )
A.点一定在直线上
B.点一定在直线上
C.点一定在平面外
D.点一定在平面内
10.给出下列四个命题,其中正确的是( )
①空间四点共面,则其中必有三点共线;②空间四点不共面,则其中任何三点不共线;③空间四点中存在三点共线,则此四点共面;④空间四点中任何三点不共线
A.②③ B.①②③ C.①② D.②③④
11. 下列命题中,正确的是 ( )
A.经过正方体任意两条面对角线,有且只有一个平面
B.经过正方体任意两条体对角线,有且只有一个平面
C.经过正方体任意两条棱,有且只有一个平面
D.经过正方体任意一条体对角线与任意一条面对角线,有且只有一个平面
12.在三棱锥的边、、、上分别取、、、四点,如果,则点( )
A.一定在直线上 B.一定在直线上
C.在直线或上 D.不在直线上,也不在直线上
13.下列说法中正确的个数是( )
①若三个平面两两相交有三条交线,则三交线相互平行;②三个平面最多将空间分为8个部分;③一平面截一正方体,则截面不可能为五边形;④过空间任意一点有且只有一条直线与两异面直线垂直
A.1 B.2 C.3 D.4
14.在三棱锥中,已知所有棱长均为,是的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
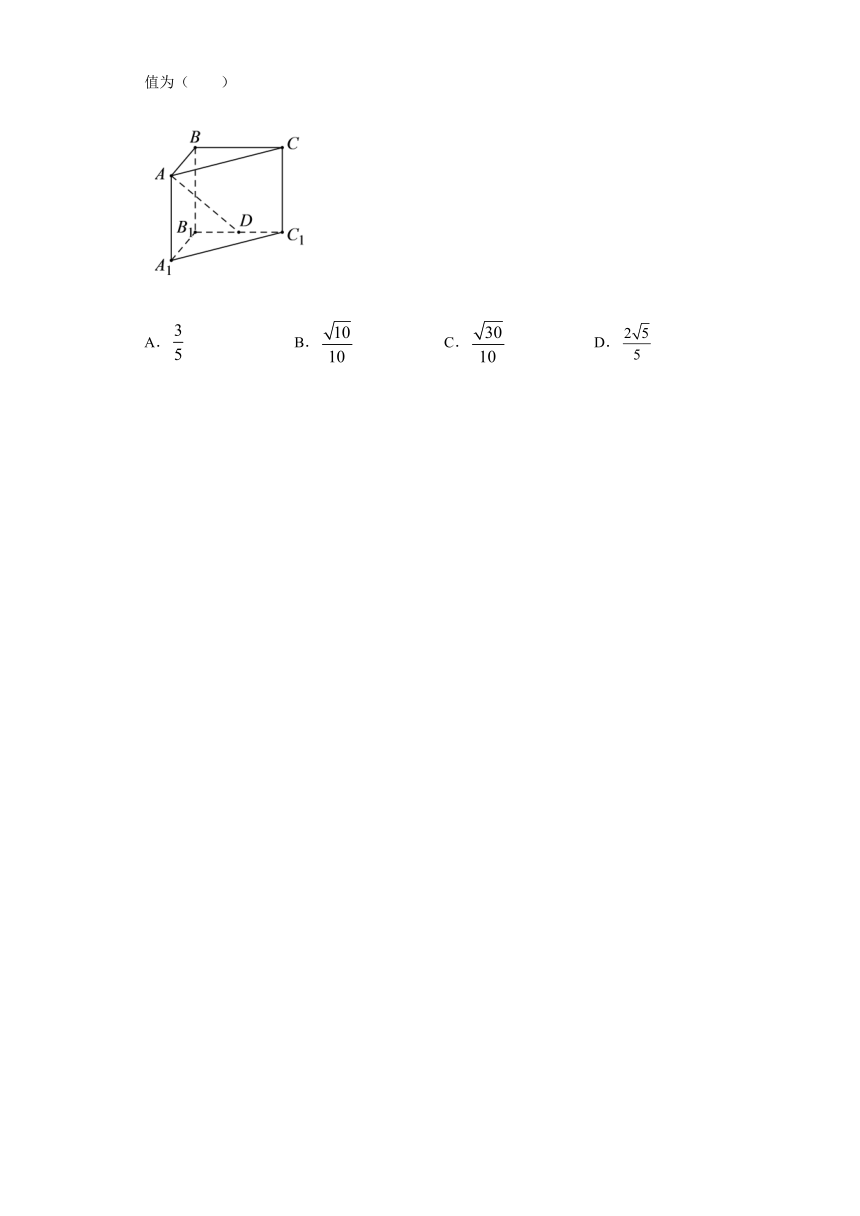
15.如图,在三棱柱中,平面,四边形为正方形,,,D为的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
参考答案
1.D
【分析】
由面面平行的定义和性质,结合空间两直线的位置关系,即可判断.
【详解】
由于平面与平面平行,且直线,
则,没有公共点,,内的直线也没有公共点,
它们可以平行或异面,
则,,错误,正确.
故选:.
2.A
【分析】
根据平面的特性和平面的画法判断.
【详解】
在立体几何中,平面是无限延展的,故①③错误;
通常我们画一个平行四边形来表示一个平面,但并不是说平面就是平行四边形,故②错误,
故选:A.
3.D
【分析】
根据平面的表示方法判断.
【详解】
③中不为对角线,故错误;⑤中漏掉“平面”两字,故错误.
故选:D.
4.C
【分析】
由空间线面位置关系,结合公理即推论,逐个验证即可.
【详解】
选项,点在是两平面的公共点,当然在交线上,故正确;
选项,由公理的推论可知,两相交直线确定一个平面,故正确;
选项,只有不共线的三点才能确定一个平面,故错误;
选项,由公理1,直线上有两点在一个平面内,则整条直线都在平面内.
故选:C
5.A
【分析】
根据确定平面的公理及其推论对选项逐个判断即可得出结果.
【详解】
三角形有且仅有3个不在同一条直线上的顶点,故其可以确定一个平面,即A正确;
当四边形为空间四边形时不能确定一个平面,故B错误;
当点在直线上时,一个点和一条直线不能确定一个平面,故C错误;
当两条直线异面时,不能确定一个平面,即D错误;
故选:A.
【点睛】
本题主要考查平面的基本定理及其推论,解题时要认真审题,仔细解答,属于基础题.
6.A
【分析】
结合图形考查两个平面的位置关系、两条直线的位置关系,以及点与线、线与面的位置关系.
【详解】
解:如图所示,两个平面与相交于直线,直线在平面内,直线和直线相交于点,
故用符号语言可表达为,,,
故选:A.
【点睛】
本题考查平面的画法及表示,点、线、面之间的位置关系的符号表示,意在考查学生的直观想象的学科素养,属基础题.
7.C
【分析】
根据平面的基本性质判断.
【详解】
两个平面若有三个公共点,当这三个点不共线时,两平面重合,当这三个点共线时,这两个平面相交或重合.
故选:C.
【点睛】
本题考查平面的基本性质,平面的基本性质公理3中一定要注意三点不共线才能确定一个平面,属于基础题.
8.A
【分析】
如果两个平面有三个公共点,那么这两个平面重合或者是相交,即可判断;利用两条异面直线不能确定一个平面即可判断;利用平面的基本性质中的公理判断即可;若两两相交的三条直线相交于同一点,则相交于同一点的三直线不一定在同一平面内(如棱锥的3条侧棱),即可判断.
【详解】
如果两个平面有三个公共点,那么这两个平面重合或者是相交,故(1)不正确;
两条异面直线不能确定一个平面,故(2)不正确;
利用平面的基本性质中的公理判断(3)正确;
空间中,若两两相交的三条直线相交于同一点,则相交于同一点的三直线不一定在同一平面内(如棱锥的3条侧棱),故(4)不正确,
综上所述只有一个说法是正确的,
故选:A.
【点睛】
本题主要考查了空间中点,线,面的位置关系.属于较易题.
9.A
【分析】
由两个面的交点在两个面的交线上,知P在两面的交线上,由AC是两平面的交线,知点P必在直线AC上.
【详解】
解:∵EF在面ABC内,而GH在面ADC内,
且EF和GH能相交于点P,
∴P在面ABC和面ADC的交线上,
∵AC是两平面的交线,
所以点P必在直线AC上.
故选:A.
【点睛】
本题考查平面的基本性质及其推论,是基础题.解题时要认真审题,仔细解答.
10.A
【分析】
取及其内部一点(不包括边界),可判断①的正误;取三棱锥的四个顶点,可判断②的正误;利用空间中的公理可判断③的正误;由、、、四点共线可判断④的正误.综合可得出结论.
【详解】
对于命题①,如下图所示:
点为内一点,则、、、四点共面,但这四点中无任何三点共线,①错误;
对于命题②,空间四点不共面,如三棱锥的四个顶点,、、、四点中无任何三点共线,②正确;
对于命题③,如果、、三点共线,且,则这四点共面;
如果、、三点共线,且,则过点与直线有且只有一个平面.
所以,③正确;
对于命题④,取及的中点,则、、共线,④错误.
故选:A.
【点睛】
本题考查空间点共面与点共线的判断,属于基础题.
11.B
【解析】
因为正方体的四条体对角线相交于同一点(正方体的中心),因此经过正方体任意两条体对角线,有且只有一个平面,故选B.
点睛:确定平面方法: 过不在一条直线上的三点,有且只有一个平面;经过一条直线和这条直线外一点有且只有一个平面;经过两条相交直线有且只有一个平面;经过两条平行直线有且只有一个平面.
12.B
【分析】
由题意得出,平面,平面,从而可得出选项.
【详解】
由题意知平面.因为交于一点,所以平面.又因为平面,所以平面.
又因为平面平面,所以点一定在直线上.
又平面,平面,但不同时在?平面和平面中,所以.
故选:B.
【点睛】
本题主要考查了空间中点共线以及两个面的交线的问题,属于基础题.
13.B
【分析】
根据空间中线线、线面、面面位置关系,逐项判断,即可得出结果.
【详解】
①若三个平面两两相交有三条交线,则三交线相互平行,或交于一点(如三棱锥的三个侧面);故①错;
②一块豆腐切三刀,最多可且8块;因此,三个平面最多可将空间分为8个部分;故②正确;
③过正方体的一个顶点,作如图所示截面,即可得出截面为五边形,故③错;
④记直线,为空间中两异面直线,则必存在直线,使得且与相交;过直线,作平面;若直线,则必分别垂直于直线 ,;由根据线面垂直的性质,过空间中任意一点,有且只有一条直线与平面垂直,因此过空间任意一点有且只有一条直线与两异面直线垂直,故④正确;
故选:B
【点睛】
本题主要考查
14.A
【分析】
取的中点,连接、,于是得到异面直线与所成的角为,然后计算出的三条边长,并利用余弦定理计算出,即可得出答案.
【详解】
如下图所示,取的中点,连接、,
由于、分别为、的中点,则,且,
所以,异面直线与所成的角为或其补角,
三棱锥是边长为的正四面体,则、均是边长为的等边三角形,
为的中点,则,且,同理可得,
在中,由余弦定理得,
因此,异面直线与所成角的余弦值为,故选A.
【点睛】
本题考查异面直线所成角的计算,利用平移法求异面直线所成角的基本步骤如下:
(1)一作:平移直线,找出异面直线所成的角;
(2)二证:对异面直线所成的角进行说明;
(3)三计算:选择合适的三角形,并计算出三角形的边长,利用余弦定理计算所求的角.
15.C
【分析】
过点D作交于点F,连接,得到为异面直线与所成的角,在中,利用余弦定理,即可求解.
【详解】
如图所示,过点D作交于点F,连接,
则为异面直线与所成的角,
由题意,在直角中,可得,
在直角中,可得,
在直角中,可得,
在直角中,可得,
所以.
故选:C.
【点睛】
本题主要考查了异面直线所成角的求解,其中解答中熟记异面直线所成的角的概念,准确运算是解答的关键,着重考查推理与计算能力.
单选题
1.平面与平面平行,且直线,下列命题中正确的是( )
A.与内的所有直线垂直 B.与内的所有直线异面
C.与内的所有直线平行 D.与内的无数条直线平行
2.已知下列四个结论:①铺得很平的一张白纸是一个平面;②平面的形状是平行四边形;③一个平面的面积可以等于.其中正确结论的个数是( )
A. B. C. D.
3.如图所示的是平行四边形所在的平面,有下列表示方法:①平面;②平面;③平面;④平面;⑤;⑥平面.其中不正确的是( )
A.④⑤ B.③④⑤ C.②③④⑤ D.③⑤
4.下列叙述错误的是( )
A.若p∈α∩β,且α∩β=l,则p∈l.
B.若直线a∩b=A,则直线a与b能确定一个平面.
C.三点A,B,C确定一个平面.
D.若A∈l,B∈l且A∈α,B∈α则lα.
5.在空间中,下列结论正确的是( )
A.三角形确定一个平面 B.四边形确定一个平面
C.一个点和一条直线确定一个平面 D.两条直线确定一个平面
6.如图所示,用符号语言可表达为
A.,, B.,,
C.,,, D.,,,
7.两个平面若有三个公共点,则这两个平面( )
A.相交 B.重合
C.相交或重合 D.以上都不对
8.下面四个说法中,正确说法的个数为( )
(1)如果两个平面有三个公共点,那么这两个平面重合;
(2)两条直线可以确定一个平面;
(3)若,,,则;
(4)空间中,两两相交的三条直线在同一平面内.
A.1 B.2 C.3 D.4
9.四个顶点不在同一平面上的四边形中,,,,分别是边,,,上的点,如果直线,交于点,那么( )
A.点一定在直线上
B.点一定在直线上
C.点一定在平面外
D.点一定在平面内
10.给出下列四个命题,其中正确的是( )
①空间四点共面,则其中必有三点共线;②空间四点不共面,则其中任何三点不共线;③空间四点中存在三点共线,则此四点共面;④空间四点中任何三点不共线
A.②③ B.①②③ C.①② D.②③④
11. 下列命题中,正确的是 ( )
A.经过正方体任意两条面对角线,有且只有一个平面
B.经过正方体任意两条体对角线,有且只有一个平面
C.经过正方体任意两条棱,有且只有一个平面
D.经过正方体任意一条体对角线与任意一条面对角线,有且只有一个平面
12.在三棱锥的边、、、上分别取、、、四点,如果,则点( )
A.一定在直线上 B.一定在直线上
C.在直线或上 D.不在直线上,也不在直线上
13.下列说法中正确的个数是( )
①若三个平面两两相交有三条交线,则三交线相互平行;②三个平面最多将空间分为8个部分;③一平面截一正方体,则截面不可能为五边形;④过空间任意一点有且只有一条直线与两异面直线垂直
A.1 B.2 C.3 D.4
14.在三棱锥中,已知所有棱长均为,是的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
15.如图,在三棱柱中,平面,四边形为正方形,,,D为的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
参考答案
1.D
【分析】
由面面平行的定义和性质,结合空间两直线的位置关系,即可判断.
【详解】
由于平面与平面平行,且直线,
则,没有公共点,,内的直线也没有公共点,
它们可以平行或异面,
则,,错误,正确.
故选:.
2.A
【分析】
根据平面的特性和平面的画法判断.
【详解】
在立体几何中,平面是无限延展的,故①③错误;
通常我们画一个平行四边形来表示一个平面,但并不是说平面就是平行四边形,故②错误,
故选:A.
3.D
【分析】
根据平面的表示方法判断.
【详解】
③中不为对角线,故错误;⑤中漏掉“平面”两字,故错误.
故选:D.
4.C
【分析】
由空间线面位置关系,结合公理即推论,逐个验证即可.
【详解】
选项,点在是两平面的公共点,当然在交线上,故正确;
选项,由公理的推论可知,两相交直线确定一个平面,故正确;
选项,只有不共线的三点才能确定一个平面,故错误;
选项,由公理1,直线上有两点在一个平面内,则整条直线都在平面内.
故选:C
5.A
【分析】
根据确定平面的公理及其推论对选项逐个判断即可得出结果.
【详解】
三角形有且仅有3个不在同一条直线上的顶点,故其可以确定一个平面,即A正确;
当四边形为空间四边形时不能确定一个平面,故B错误;
当点在直线上时,一个点和一条直线不能确定一个平面,故C错误;
当两条直线异面时,不能确定一个平面,即D错误;
故选:A.
【点睛】
本题主要考查平面的基本定理及其推论,解题时要认真审题,仔细解答,属于基础题.
6.A
【分析】
结合图形考查两个平面的位置关系、两条直线的位置关系,以及点与线、线与面的位置关系.
【详解】
解:如图所示,两个平面与相交于直线,直线在平面内,直线和直线相交于点,
故用符号语言可表达为,,,
故选:A.
【点睛】
本题考查平面的画法及表示,点、线、面之间的位置关系的符号表示,意在考查学生的直观想象的学科素养,属基础题.
7.C
【分析】
根据平面的基本性质判断.
【详解】
两个平面若有三个公共点,当这三个点不共线时,两平面重合,当这三个点共线时,这两个平面相交或重合.
故选:C.
【点睛】
本题考查平面的基本性质,平面的基本性质公理3中一定要注意三点不共线才能确定一个平面,属于基础题.
8.A
【分析】
如果两个平面有三个公共点,那么这两个平面重合或者是相交,即可判断;利用两条异面直线不能确定一个平面即可判断;利用平面的基本性质中的公理判断即可;若两两相交的三条直线相交于同一点,则相交于同一点的三直线不一定在同一平面内(如棱锥的3条侧棱),即可判断.
【详解】
如果两个平面有三个公共点,那么这两个平面重合或者是相交,故(1)不正确;
两条异面直线不能确定一个平面,故(2)不正确;
利用平面的基本性质中的公理判断(3)正确;
空间中,若两两相交的三条直线相交于同一点,则相交于同一点的三直线不一定在同一平面内(如棱锥的3条侧棱),故(4)不正确,
综上所述只有一个说法是正确的,
故选:A.
【点睛】
本题主要考查了空间中点,线,面的位置关系.属于较易题.
9.A
【分析】
由两个面的交点在两个面的交线上,知P在两面的交线上,由AC是两平面的交线,知点P必在直线AC上.
【详解】
解:∵EF在面ABC内,而GH在面ADC内,
且EF和GH能相交于点P,
∴P在面ABC和面ADC的交线上,
∵AC是两平面的交线,
所以点P必在直线AC上.
故选:A.
【点睛】
本题考查平面的基本性质及其推论,是基础题.解题时要认真审题,仔细解答.
10.A
【分析】
取及其内部一点(不包括边界),可判断①的正误;取三棱锥的四个顶点,可判断②的正误;利用空间中的公理可判断③的正误;由、、、四点共线可判断④的正误.综合可得出结论.
【详解】
对于命题①,如下图所示:
点为内一点,则、、、四点共面,但这四点中无任何三点共线,①错误;
对于命题②,空间四点不共面,如三棱锥的四个顶点,、、、四点中无任何三点共线,②正确;
对于命题③,如果、、三点共线,且,则这四点共面;
如果、、三点共线,且,则过点与直线有且只有一个平面.
所以,③正确;
对于命题④,取及的中点,则、、共线,④错误.
故选:A.
【点睛】
本题考查空间点共面与点共线的判断,属于基础题.
11.B
【解析】
因为正方体的四条体对角线相交于同一点(正方体的中心),因此经过正方体任意两条体对角线,有且只有一个平面,故选B.
点睛:确定平面方法: 过不在一条直线上的三点,有且只有一个平面;经过一条直线和这条直线外一点有且只有一个平面;经过两条相交直线有且只有一个平面;经过两条平行直线有且只有一个平面.
12.B
【分析】
由题意得出,平面,平面,从而可得出选项.
【详解】
由题意知平面.因为交于一点,所以平面.又因为平面,所以平面.
又因为平面平面,所以点一定在直线上.
又平面,平面,但不同时在?平面和平面中,所以.
故选:B.
【点睛】
本题主要考查了空间中点共线以及两个面的交线的问题,属于基础题.
13.B
【分析】
根据空间中线线、线面、面面位置关系,逐项判断,即可得出结果.
【详解】
①若三个平面两两相交有三条交线,则三交线相互平行,或交于一点(如三棱锥的三个侧面);故①错;
②一块豆腐切三刀,最多可且8块;因此,三个平面最多可将空间分为8个部分;故②正确;
③过正方体的一个顶点,作如图所示截面,即可得出截面为五边形,故③错;
④记直线,为空间中两异面直线,则必存在直线,使得且与相交;过直线,作平面;若直线,则必分别垂直于直线 ,;由根据线面垂直的性质,过空间中任意一点,有且只有一条直线与平面垂直,因此过空间任意一点有且只有一条直线与两异面直线垂直,故④正确;
故选:B
【点睛】
本题主要考查
14.A
【分析】
取的中点,连接、,于是得到异面直线与所成的角为,然后计算出的三条边长,并利用余弦定理计算出,即可得出答案.
【详解】
如下图所示,取的中点,连接、,
由于、分别为、的中点,则,且,
所以,异面直线与所成的角为或其补角,
三棱锥是边长为的正四面体,则、均是边长为的等边三角形,
为的中点,则,且,同理可得,
在中,由余弦定理得,
因此,异面直线与所成角的余弦值为,故选A.
【点睛】
本题考查异面直线所成角的计算,利用平移法求异面直线所成角的基本步骤如下:
(1)一作:平移直线,找出异面直线所成的角;
(2)二证:对异面直线所成的角进行说明;
(3)三计算:选择合适的三角形,并计算出三角形的边长,利用余弦定理计算所求的角.
15.C
【分析】
过点D作交于点F,连接,得到为异面直线与所成的角,在中,利用余弦定理,即可求解.
【详解】
如图所示,过点D作交于点F,连接,
则为异面直线与所成的角,
由题意,在直角中,可得,
在直角中,可得,
在直角中,可得,
在直角中,可得,
所以.
故选:C.
【点睛】
本题主要考查了异面直线所成角的求解,其中解答中熟记异面直线所成的角的概念,准确运算是解答的关键,着重考查推理与计算能力.
