1.3.1简单的组合体-北师大版高中数学必修二基础练习(Word含答案解析)
文档属性
| 名称 | 1.3.1简单的组合体-北师大版高中数学必修二基础练习(Word含答案解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 00:00:00 | ||
图片预览


文档简介
1.3.1简单的组合体基础练习题
一、单选题
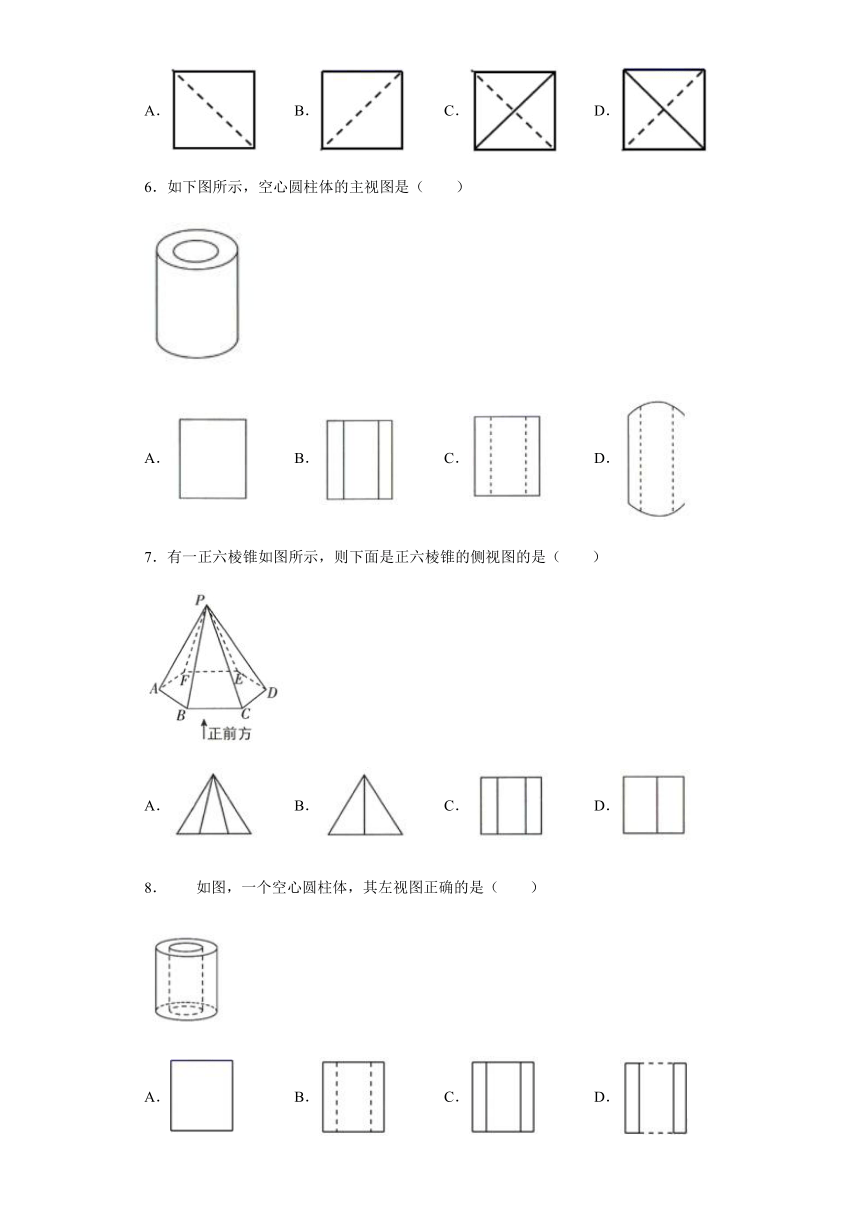
1.如图所示的组合体,其结构特征是( )
A.由两个圆锥组合成的
B.由两个圆柱组合成的
C.由一个棱锥和一个棱柱组合成的
D.由一个圆锥和一个圆柱组合成的
2.如图是一几何体的直观图、正视图和俯视图.在正视图右侧,按照画三视图的要求画出的该几何体的侧视图是( )
A. B.
C. D.
3.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的侧视图是( )
A. B.
C. D.
4.如图的组合体是由( )组合而成.
A.两个棱柱 B.棱柱和圆柱
C.圆柱和棱台 D.圆锥和棱柱
5.某正方体被截去部分后剩余几何体的直观图如图所示,则该几何体的侧视图为( )
A. B. C. D.
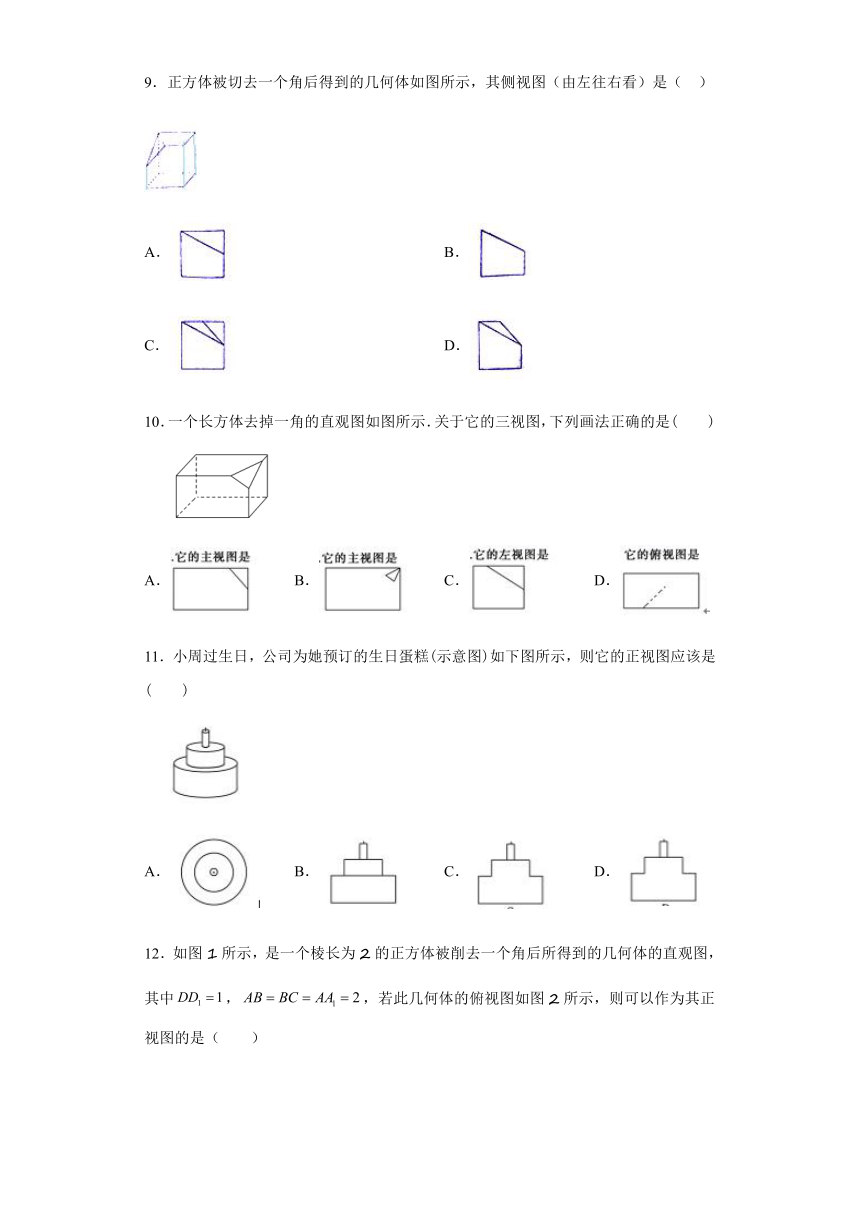
6.如下图所示,空心圆柱体的主视图是( )
A. B. C. D.
7.有一正六棱锥如图所示,则下面是正六棱锥的侧视图的是( )
A. B. C. D.
8.如图,一个空心圆柱体,其左视图正确的是( )
A. B. C. D.
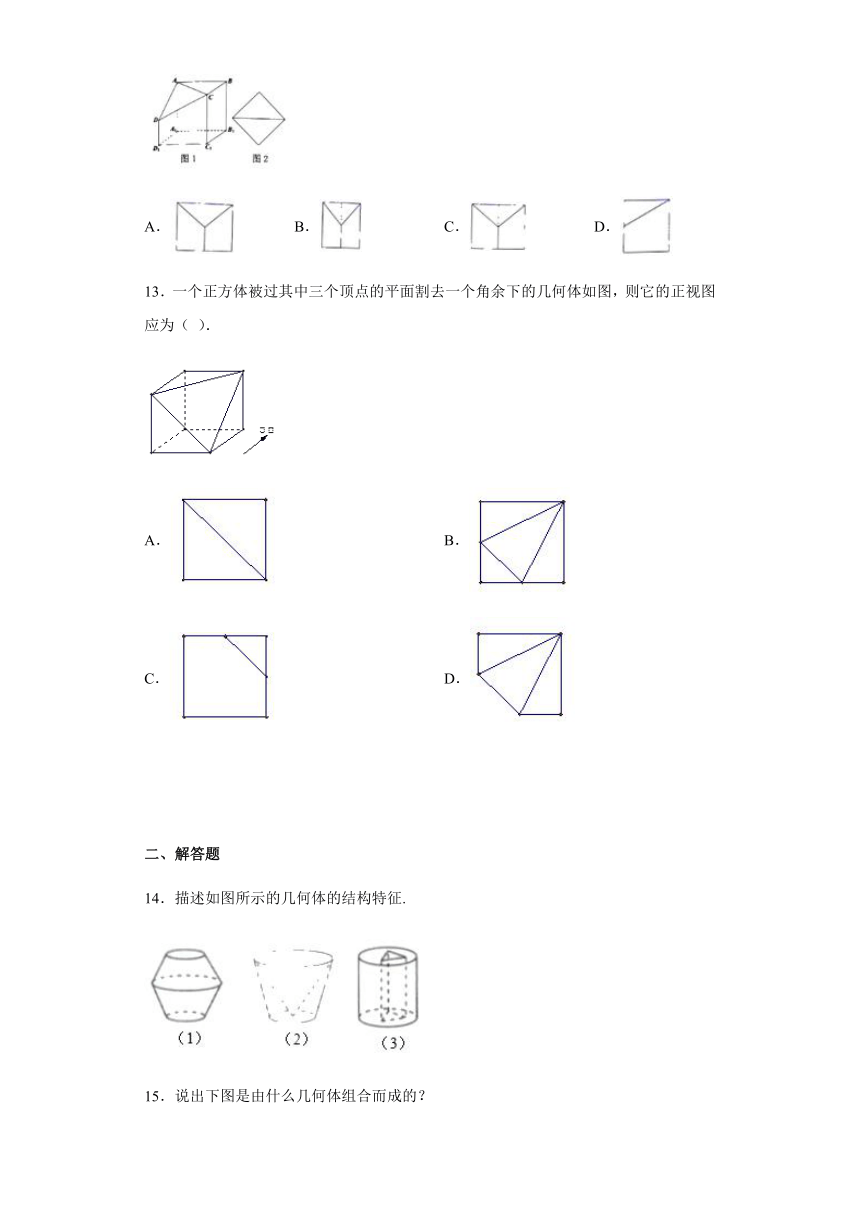
9.正方体被切去一个角后得到的几何体如图所示,其侧视图(由左往右看)是( )
A. B.
C. D.
10.一个长方体去掉一角的直观图如图所示.关于它的三视图,下列画法正确的是( )
A. B. C. D.
11.小周过生日,公司为她预订的生日蛋糕(示意图)如下图所示,则它的正视图应该是 ( )
A. B. C. D.
12.如图1所示,是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图,其中,,若此几何体的俯视图如图2所示,则可以作为其正视图的是( )
A. B. C. D.
13.一个正方体被过其中三个顶点的平面割去一个角余下的几何体如图,则它的正视图应为( ).
A. B.
C. D.
二、解答题
14.描述如图所示的几何体的结构特征.
15.说出下图是由什么几何体组合而成的?
16. 画出下图中几何体的三视图.
参考答案
1.D
【分析】
根据圆柱和圆锥的特征即可判断.
【详解】
由图知:该组合体是由一个圆锥和一个圆柱组合成的,
故选:D
2.B
【分析】
根据正视图和俯视图易得两两垂直,进而得到侧视图的投影面是平面APD求解.
【详解】
由正视图和俯视图知:两两垂直,
所以侧视图的投影面为平面APD,
又平面ABCD,又 ,且侧视图从左向右,
故选:B
3.B
【分析】
本题根据三视图的定义直接选答案即可.
【详解】
解:根据三视图的定义直接选B.
故选:B
【点睛】
本题考查几何体的三视图识别,是基础题.
4.B
【分析】
根据组合体的结构特征即可求解.
【详解】
由图可知该组合体由圆柱和六棱柱组合而成,
故选:B
【点睛】
本题考查了组合体的结构特征,考查了基本知识的掌握情况,属于基础题.
5.B
【分析】
根据三视图的特点:长对正,高平齐,宽相等分析求解.
【详解】
由三视图的画法,可得侧视图如下:
故选:B
【点睛】
本题主要考查三视图,还考查了空间想象的能力,属于基础题.
6.C
【分析】
根据几何体内的空心圆柱的轮廓是一个看不见的矩形,可知用虚线表示即可.
【详解】
圆柱体的主视图是矩形,因为是空心圆柱,所以要用虚线体现出中间的轮廓线.
故选C.
【点睛】
本题考查了几何体的主视图的作法,注意不可见轮廓用虚线表示,属于基础题.
7.B
【分析】
根据侧视图的意义,从左看几何体所得的轮廓可以推出.
【详解】
正六棱锥的侧视图的是由两个△PFA和△PBA在竖直平面内的正投影,是由两个直角三角形组成的图形,PA的投影是实线,因此选B.
故选B.
【点睛】
本题考查了几何体的侧视图的作法,要掌握侧视图是从左看几何体的侧面在竖直平面上的正投影,本题属于基础题.
8.B
【分析】
从左侧观察空心圆柱体,能够看见的部分用实线表示,不能看见的部分用虚线表示,即可得到左视图.
【详解】
左视图是在几何体左侧面观察物体得到的图形。能够看见的部分用实线表示,不能看见的部分用虚线表示。本题圆柱体的左视图整体是个矩形,中间包含两条竖直的虚线。
故本题正确答案为B。
【点睛】
本题主要考查三视图, 主视图是在物体正面从前向后观察物体得到的图形;俯视图是在水平面内从上向下观察物体得到的图形;左视图是在几何体左侧面观察物体得到的图形。
9.A
【解析】
【分析】
根据侧视图是从左往右看到的图形即可得出结果.
【详解】
从左往右看,是正方形从左上角有一条斜线.
故选A
【点睛】
本题主要考查几何体的三视图,熟记常见几何体的三视图即可,属于基础题型.
10.A
【解析】
【分析】
从去掉一角的长方体的正面、左侧、上方观察,分别可得主视图、左视图、俯视图。
【详解】
因为主视图中,应是长方形中一条线段,而不能是三角形,所以选项B错误;因为左视图中的线应为虚线,所以选项C错误;因为俯视图是实线,所以选项D错误。
故选A。
【点睛】
本题考查几何体的三视图。由几何体的直观图得到三视图,可以想象分别从正面、左侧、上方观察几何体的正投影分别是什么。注意被几何体挡住的线应该画成虚线。
11.B
【解析】
A为俯视图,注意到封闭的线段情形,正视图应该是B.
本题选择B选项.
12.C
【解析】
由题意,根据该几何体的直观图和俯视图知,其正视图的长应为底面正方形的对角线长,宽应为正方体的棱长,故排除B,D,而在三视图中看不见的棱用虚线表示,故排除A,所以正确答案为C.
点睛:此题主要考查空间几何体的三视图等有关方面的知识,属于中低档题型,也是最近几年高考的必考题型.此题有与以往有不同之处,就是给出了空间几何体的三视图各俯视图,去寻找正视图,注意的是,由实物图画三视图或判断选择三视图时,需要注意“长对正、高平齐、宽相等”的原则,还看得见棱的画实线,看不见的棱要画虚线.
13.A
【分析】
根据正视图的定义可得正确的选项.
【详解】
正视图应为正方形且正方形的对角线相连,故选A.
【点睛】
本题考查三视图,属于容易题.
14.见解析.
【分析】
根据图形的对称性,结合虚实线,即可得出结论.
【详解】
(1)是将两个完全相同的圆台的较大底面重合拼接而成的简单组合体.
(2)是由一个圆台挖去一个底面与圆台上底面重合,顶点为圆台下底面圆心的圆锥后得到的简单组合体.
(3)是由一个圆柱中挖去一个两底面分别在圆柱两底面内的三棱柱后得到的简单组合体.
【点睛】
本题考查组合体的结构特征,属于基础题.
15.①三棱柱挖去一个圆柱②球、圆柱和圆台
【解析】
试题分析:根据三棱柱,圆柱,球及圆台的概念可得解.
试题解析:
①三棱柱挖去一个圆柱②球、圆柱和圆台
16.见解析
【解析】
试题分析:三视图关键掌握从正视、侧视、俯视的图形观察,该题结合组合体由圆柱和三个小正方体合成的特征,画出三视图,注意看不到的线用虚线表示。
试题解析:
图中几何体组合体,下部是三个正方体,上部是一个圆柱,按照正方体和圆柱的三视图的画法画出该组合体的三视图.
该几何体的三视图如图所示.
一、单选题
1.如图所示的组合体,其结构特征是( )
A.由两个圆锥组合成的
B.由两个圆柱组合成的
C.由一个棱锥和一个棱柱组合成的
D.由一个圆锥和一个圆柱组合成的
2.如图是一几何体的直观图、正视图和俯视图.在正视图右侧,按照画三视图的要求画出的该几何体的侧视图是( )
A. B.
C. D.
3.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的侧视图是( )
A. B.
C. D.
4.如图的组合体是由( )组合而成.
A.两个棱柱 B.棱柱和圆柱
C.圆柱和棱台 D.圆锥和棱柱
5.某正方体被截去部分后剩余几何体的直观图如图所示,则该几何体的侧视图为( )
A. B. C. D.
6.如下图所示,空心圆柱体的主视图是( )
A. B. C. D.
7.有一正六棱锥如图所示,则下面是正六棱锥的侧视图的是( )
A. B. C. D.
8.如图,一个空心圆柱体,其左视图正确的是( )
A. B. C. D.
9.正方体被切去一个角后得到的几何体如图所示,其侧视图(由左往右看)是( )
A. B.
C. D.
10.一个长方体去掉一角的直观图如图所示.关于它的三视图,下列画法正确的是( )
A. B. C. D.
11.小周过生日,公司为她预订的生日蛋糕(示意图)如下图所示,则它的正视图应该是 ( )
A. B. C. D.
12.如图1所示,是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图,其中,,若此几何体的俯视图如图2所示,则可以作为其正视图的是( )
A. B. C. D.
13.一个正方体被过其中三个顶点的平面割去一个角余下的几何体如图,则它的正视图应为( ).
A. B.
C. D.
二、解答题
14.描述如图所示的几何体的结构特征.
15.说出下图是由什么几何体组合而成的?
16. 画出下图中几何体的三视图.
参考答案
1.D
【分析】
根据圆柱和圆锥的特征即可判断.
【详解】
由图知:该组合体是由一个圆锥和一个圆柱组合成的,
故选:D
2.B
【分析】
根据正视图和俯视图易得两两垂直,进而得到侧视图的投影面是平面APD求解.
【详解】
由正视图和俯视图知:两两垂直,
所以侧视图的投影面为平面APD,
又平面ABCD,又 ,且侧视图从左向右,
故选:B
3.B
【分析】
本题根据三视图的定义直接选答案即可.
【详解】
解:根据三视图的定义直接选B.
故选:B
【点睛】
本题考查几何体的三视图识别,是基础题.
4.B
【分析】
根据组合体的结构特征即可求解.
【详解】
由图可知该组合体由圆柱和六棱柱组合而成,
故选:B
【点睛】
本题考查了组合体的结构特征,考查了基本知识的掌握情况,属于基础题.
5.B
【分析】
根据三视图的特点:长对正,高平齐,宽相等分析求解.
【详解】
由三视图的画法,可得侧视图如下:
故选:B
【点睛】
本题主要考查三视图,还考查了空间想象的能力,属于基础题.
6.C
【分析】
根据几何体内的空心圆柱的轮廓是一个看不见的矩形,可知用虚线表示即可.
【详解】
圆柱体的主视图是矩形,因为是空心圆柱,所以要用虚线体现出中间的轮廓线.
故选C.
【点睛】
本题考查了几何体的主视图的作法,注意不可见轮廓用虚线表示,属于基础题.
7.B
【分析】
根据侧视图的意义,从左看几何体所得的轮廓可以推出.
【详解】
正六棱锥的侧视图的是由两个△PFA和△PBA在竖直平面内的正投影,是由两个直角三角形组成的图形,PA的投影是实线,因此选B.
故选B.
【点睛】
本题考查了几何体的侧视图的作法,要掌握侧视图是从左看几何体的侧面在竖直平面上的正投影,本题属于基础题.
8.B
【分析】
从左侧观察空心圆柱体,能够看见的部分用实线表示,不能看见的部分用虚线表示,即可得到左视图.
【详解】
左视图是在几何体左侧面观察物体得到的图形。能够看见的部分用实线表示,不能看见的部分用虚线表示。本题圆柱体的左视图整体是个矩形,中间包含两条竖直的虚线。
故本题正确答案为B。
【点睛】
本题主要考查三视图, 主视图是在物体正面从前向后观察物体得到的图形;俯视图是在水平面内从上向下观察物体得到的图形;左视图是在几何体左侧面观察物体得到的图形。
9.A
【解析】
【分析】
根据侧视图是从左往右看到的图形即可得出结果.
【详解】
从左往右看,是正方形从左上角有一条斜线.
故选A
【点睛】
本题主要考查几何体的三视图,熟记常见几何体的三视图即可,属于基础题型.
10.A
【解析】
【分析】
从去掉一角的长方体的正面、左侧、上方观察,分别可得主视图、左视图、俯视图。
【详解】
因为主视图中,应是长方形中一条线段,而不能是三角形,所以选项B错误;因为左视图中的线应为虚线,所以选项C错误;因为俯视图是实线,所以选项D错误。
故选A。
【点睛】
本题考查几何体的三视图。由几何体的直观图得到三视图,可以想象分别从正面、左侧、上方观察几何体的正投影分别是什么。注意被几何体挡住的线应该画成虚线。
11.B
【解析】
A为俯视图,注意到封闭的线段情形,正视图应该是B.
本题选择B选项.
12.C
【解析】
由题意,根据该几何体的直观图和俯视图知,其正视图的长应为底面正方形的对角线长,宽应为正方体的棱长,故排除B,D,而在三视图中看不见的棱用虚线表示,故排除A,所以正确答案为C.
点睛:此题主要考查空间几何体的三视图等有关方面的知识,属于中低档题型,也是最近几年高考的必考题型.此题有与以往有不同之处,就是给出了空间几何体的三视图各俯视图,去寻找正视图,注意的是,由实物图画三视图或判断选择三视图时,需要注意“长对正、高平齐、宽相等”的原则,还看得见棱的画实线,看不见的棱要画虚线.
13.A
【分析】
根据正视图的定义可得正确的选项.
【详解】
正视图应为正方形且正方形的对角线相连,故选A.
【点睛】
本题考查三视图,属于容易题.
14.见解析.
【分析】
根据图形的对称性,结合虚实线,即可得出结论.
【详解】
(1)是将两个完全相同的圆台的较大底面重合拼接而成的简单组合体.
(2)是由一个圆台挖去一个底面与圆台上底面重合,顶点为圆台下底面圆心的圆锥后得到的简单组合体.
(3)是由一个圆柱中挖去一个两底面分别在圆柱两底面内的三棱柱后得到的简单组合体.
【点睛】
本题考查组合体的结构特征,属于基础题.
15.①三棱柱挖去一个圆柱②球、圆柱和圆台
【解析】
试题分析:根据三棱柱,圆柱,球及圆台的概念可得解.
试题解析:
①三棱柱挖去一个圆柱②球、圆柱和圆台
16.见解析
【解析】
试题分析:三视图关键掌握从正视、侧视、俯视的图形观察,该题结合组合体由圆柱和三个小正方体合成的特征,画出三视图,注意看不到的线用虚线表示。
试题解析:
图中几何体组合体,下部是三个正方体,上部是一个圆柱,按照正方体和圆柱的三视图的画法画出该组合体的三视图.
该几何体的三视图如图所示.
