1.7.1柱、锥、台的侧面展开与面积-北师大版高中数学必修二基础练习(Word含答案解析)
文档属性
| 名称 | 1.7.1柱、锥、台的侧面展开与面积-北师大版高中数学必修二基础练习(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 481.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 00:00:00 | ||
图片预览




文档简介
1.7.1柱、锥、台的侧面展开与面积基础检测题
一、单选题
1.已知某圆柱底面的半径为1,高为2,则该圆柱的表面积为( )
A. B. C. D.
2.若圆锥的高等于底面圆半径,则它的底面积与侧面积之比是( )
A. B. C. D.
3.现有同底等高的圆锥和圆柱,已知圆柱的轴截面是边长为2的正方形,则圆锥的侧面积为( )
A. B. C. D.
4.圆柱的母线长为,底面半径为,则圆柱的侧面积为( )
A. B. C. D.
5.某几何体的三视图如图所示,则该几何体的表面积为
A. B. C. D.
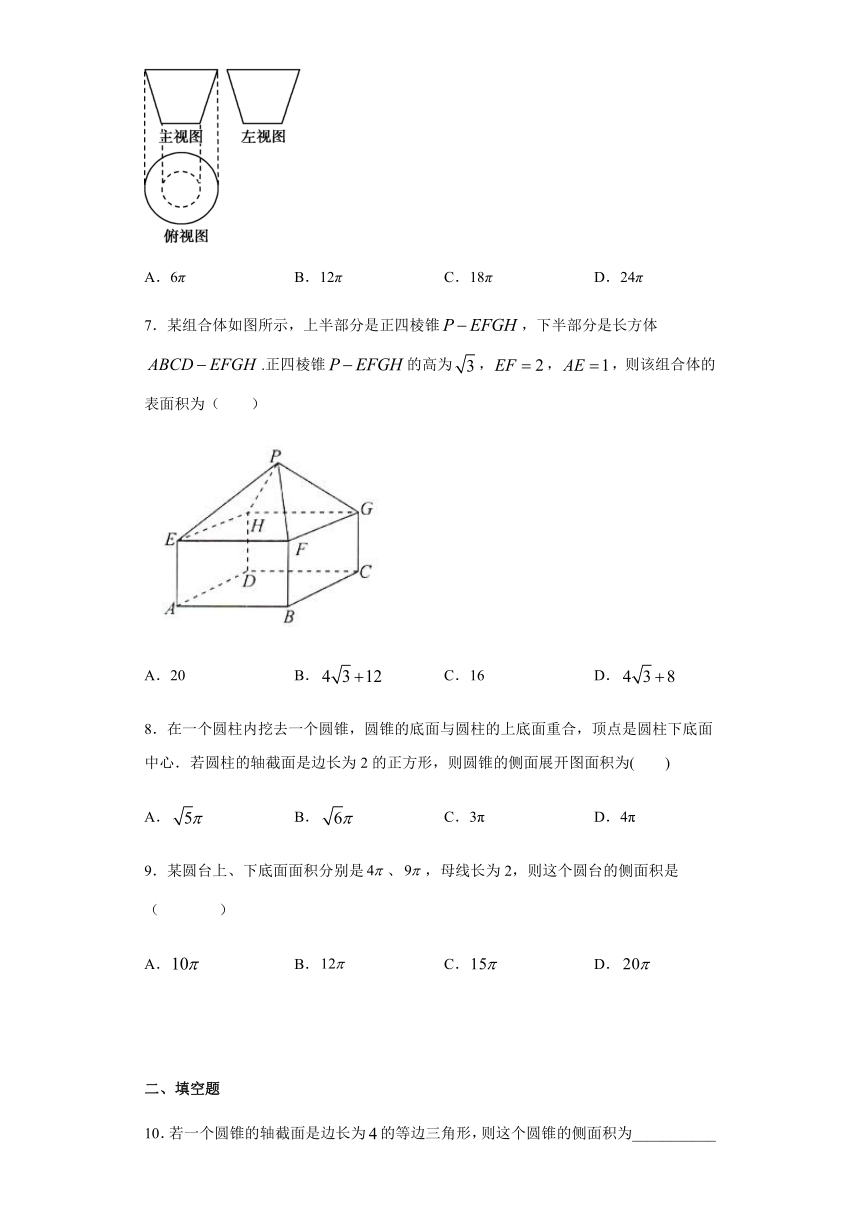
6.一个几何体的三视图如图所示,其主视图和左视图都是底边长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
A.6π B.12π C.18π D.24π
7.某组合体如图所示,上半部分是正四棱锥,下半部分是长方体.正四棱锥的高为,,,则该组合体的表面积为( )
A.20 B. C.16 D.
8.在一个圆柱内挖去一个圆锥,圆锥的底面与圆柱的上底面重合,顶点是圆柱下底面中心.若圆柱的轴截面是边长为2的正方形,则圆锥的侧面展开图面积为( )
A. B. C.3π D.4π
9.某圆台上、下底面面积分别是、,母线长为2,则这个圆台的侧面积是( )
A. B. C. D.
二、填空题
10.若一个圆锥的轴截面是边长为的等边三角形,则这个圆锥的侧面积为___________
11.已知一个半圆柱的高为4,其俯视图如图所示,侧视图的面积为8,则该半圆柱的底面半圆的半径为__________.
12.底面边长和高都为2的正四棱锥的表面积为____________.
13.若一个圆台的母线长为l,上、下底面半径,满足,且圆台的侧面积为,则__________.
三、解答题
14.已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,求该四棱台的表面积.
15.在底面半径为2,高为的圆锥中内接一个圆柱,且圆柱的底面积与圆锥的底面积之比为1:4,求圆柱的表面积.
16.现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的侧面积.
17.已知圆台的上、下底面半径分别是2,6,且侧面面积等于两底面面积之和.
(1)求圆台的母线长.
(2)求圆台的表面积.
18.侧面都是等腰直角三角形的正三棱锥,底面边长为时,求该棱锥的表面积.
参考答案
1.C
【分析】
根据圆柱表面积的计算公式直接求解即可.
【详解】
解:因为圆柱的底面半径为1,高为2,
所以圆柱的表面积.
故选:C.
【点睛】
本题考查了圆柱表面积的求法,属基础题.
2.C
【分析】
设圆锥的底面半径为,用将圆锥的底面积及侧面积分别表示即可得到答案.
【详解】
设圆锥的底面半径为,则高为,母线长 则,
, ,
故选:C .
3.D
【分析】
由已知条件知,圆锥的高和底面直径都为2,即可求圆锥的母线长,利用圆锥侧面积公式求面积即可.
【详解】
同底等高的圆锥和圆柱,圆柱的轴截面是边长为2的正方形,知:圆锥的高和底面直径都为2,
∴圆锥的母线长为:,
有侧面积.
故选:D
【点睛】
本题考查了圆锥侧面积的求法,结合圆柱、正方形的性质,并应用了圆锥侧面积公式,属于简单题.
4.A
【分析】
根据圆柱的侧面积公式计算即可.
【详解】
圆柱的母线长为,底面半径为,
则圆柱的侧面积为.
故选:A
【点睛】
本小题主要考查圆柱的侧面积公式,属于基础题.
5.A
【分析】
由三视图还原,可知该几何体是半圆柱,利用公式求其表面积即可.
【详解】
由三视图还原,可知该几何体是半圆柱,
半圆柱的底面半径为,高为2,
=
故选:A
【点睛】
本题主要考查了三视图--长对正、宽平齐、高相等得到实物图中的数据,由三视图还原实物图处理问题.还考查了表面积计算,属于基础题.
6.B
【分析】
该几何体的直观图是圆台,上底面是一个直径为2的圆,下底面是一个直径为4的圆,母线长是4,利用圆台的侧面积公式即得解.
【详解】
由三视图可知,正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,该几何体的直观图是圆台,上底面是一个直径为2的圆,下底面是一个直径为4的圆,母线长是4,
其圆台的侧面积是:.
故选:B.
【点睛】
本题主要考查三视图还原几何体,考查圆台的侧面积,意在考查学生对这些知识的理解掌握水平.
7.A
【分析】
该组合体由一个正四棱锥和一个长方体组成,由勾股定理可计算出正四棱锥的斜高,即可运用三角形的面积公式求出正四棱锥的侧面积,再求出长方体的侧面积和底面积,再求和即可.
【详解】
由题意,正四棱锥的斜高为,该组合体的表面积为.
故选:A
【点睛】
本题考查了组合体的表面积,求四棱锥的斜高是关键,考查了运算能力和空间想象能力,属于中档题.
8.A
【分析】
由已知得到圆锥的半径与母线长,再代入扇形面积公式求得圆锥侧展图面积.
【详解】
圆锥的侧面展开图是半径为,弧长为的扇形,其面积,所以圆锥的侧面展开图面积为.
【点睛】
本题考查求圆锥侧展图及扇形面积的基本运算.
9.A
【分析】
先根据圆台上、下底面面积分别是、,求出圆台上、下底面的半径,再由公式求圆台的侧面积.
【详解】
设圆台上、下底面的半径分别为,
由圆台上、下底面面积分别是、,则
所以
所以这个圆台的侧面积为
故选:A
【点睛】
本题考查求圆台的侧面积,直接利用公式,属于基础题.
10.
【分析】
利用圆锥的性质求出底面半径与母线长,再利用圆锥的侧面积计算公式即可得出.
【详解】
轴截面是边长为4等边三角形,
所以圆锥底面半径,
圆锥母线.
圆锥的侧面积.
故答案为:.
【点睛】
本题主要考查圆锥侧面积的求解,熟练掌握圆锥的性质及圆锥的侧面积的计算公式是解题的关键.
11.
【分析】
由题意可知,该半圆柱的侧视图为底边长为底面圆半径,高为的矩形,则根据侧视图的面积即可求得底面圆的半径.
【详解】
因为该半圆柱的高为,侧视图的面积为,则底面圆的半径为.
故答案为:.
【点睛】
本题考查与几何体的三视图有关的计算问题,属于简单题.
12.
【分析】
求出斜高,计算各面的面积,求和可得正四棱锥的表面积.
【详解】
如图所示,,则,,
故正四棱锥的表面积为.
故答案为:
【点睛】
本题考查了求正四棱锥的表面积,属于基础题.
13.2
【分析】
根据圆台的侧面积公式计算.
【详解】
由题意,解得.
故答案为:2.
【点睛】
本题考查圆台的侧面积公式,属于基础题.
14.
【分析】
首先求出四棱台上、下底面面积与侧面面积,然后求出表面积即可.
【详解】
如图,
在四棱台中,
过作,垂足为,
在中,,,
故,
所以,
故四棱台的侧面积,
所以四棱台的表面积.
【点睛】
本题考查了四棱台的表面积,属于基础题.
15.
【分析】
由圆柱、圆锥的底面面积比可得圆柱的底面半径和高分别为1、,进而求其表面积即可.
【详解】
由圆柱的底面积与圆锥的底面积之比为1:4,知:底面半径比为1:2,
即圆柱底面半径,若设圆柱的高为,则有,即,
∴由圆柱的表面积等于侧面积加上两底面的面积,
即:.
【点睛】
本题考查了圆柱的表面积计算,由圆锥内接圆柱及底面面积比求圆柱表面积,属于简单题.
16.160
【分析】
由于该直四棱柱的底面是菱形,所以求其中一个侧面的面积乘以4即可,由菱形其对角线垂直于勾股定理求得底面边长,再由矩形面积公式求得答案.
【详解】
如图,设底面对角线AC=a,BD=b,交点为O,对角线A1C=15,B1D=9,
∴a2+52=152,b2+52=92,∴a2=200,b2=56.
∵该直四棱柱的底面是菱形,
∴AB2====64,∴AB=8.
∴直四棱柱的侧面积S=4×8×5=160.
【点睛】
本题考查求直四棱柱的侧面积,属于基础题.
17.(1)5(2)80π
【分析】
(1)由圆台的侧面积公式与两底面圆的面积之和的关系构建方程,求得母线;
(2)由(1)可得圆台的母线,再由圆台的表面积的公式求得答案.
【详解】
(1)设圆台的母线长为l,则由题意得π(2+6)l=π×22+π×62,
∴8πl=40π,∴l=5,∴该圆台的母线长为5;
(2)由(1)可得圆台的表面积为S=π×(2+6)×5+π·22+π×62=40π+4π+36π=80π.
【点睛】
本题考查由圆台的性质求圆台的母线与表面积,属于基础题.
18.
【分析】
先求三个侧面的面积,再求解底面积,从而可得棱锥的表面积.
【详解】
∵正三棱锥的侧面都是等腰直角三角形,且底面边长为,
∴侧棱长等于,∴该棱锥的表面积.
【点睛】
本题主要考查三棱锥表面积的求解,表面积包含侧面积和底面积,侧面积可利用侧面积公式求解,侧重考查数学运算的核心素养.
一、单选题
1.已知某圆柱底面的半径为1,高为2,则该圆柱的表面积为( )
A. B. C. D.
2.若圆锥的高等于底面圆半径,则它的底面积与侧面积之比是( )
A. B. C. D.
3.现有同底等高的圆锥和圆柱,已知圆柱的轴截面是边长为2的正方形,则圆锥的侧面积为( )
A. B. C. D.
4.圆柱的母线长为,底面半径为,则圆柱的侧面积为( )
A. B. C. D.
5.某几何体的三视图如图所示,则该几何体的表面积为
A. B. C. D.
6.一个几何体的三视图如图所示,其主视图和左视图都是底边长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
A.6π B.12π C.18π D.24π
7.某组合体如图所示,上半部分是正四棱锥,下半部分是长方体.正四棱锥的高为,,,则该组合体的表面积为( )
A.20 B. C.16 D.
8.在一个圆柱内挖去一个圆锥,圆锥的底面与圆柱的上底面重合,顶点是圆柱下底面中心.若圆柱的轴截面是边长为2的正方形,则圆锥的侧面展开图面积为( )
A. B. C.3π D.4π
9.某圆台上、下底面面积分别是、,母线长为2,则这个圆台的侧面积是( )
A. B. C. D.
二、填空题
10.若一个圆锥的轴截面是边长为的等边三角形,则这个圆锥的侧面积为___________
11.已知一个半圆柱的高为4,其俯视图如图所示,侧视图的面积为8,则该半圆柱的底面半圆的半径为__________.
12.底面边长和高都为2的正四棱锥的表面积为____________.
13.若一个圆台的母线长为l,上、下底面半径,满足,且圆台的侧面积为,则__________.
三、解答题
14.已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,求该四棱台的表面积.
15.在底面半径为2,高为的圆锥中内接一个圆柱,且圆柱的底面积与圆锥的底面积之比为1:4,求圆柱的表面积.
16.现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的侧面积.
17.已知圆台的上、下底面半径分别是2,6,且侧面面积等于两底面面积之和.
(1)求圆台的母线长.
(2)求圆台的表面积.
18.侧面都是等腰直角三角形的正三棱锥,底面边长为时,求该棱锥的表面积.
参考答案
1.C
【分析】
根据圆柱表面积的计算公式直接求解即可.
【详解】
解:因为圆柱的底面半径为1,高为2,
所以圆柱的表面积.
故选:C.
【点睛】
本题考查了圆柱表面积的求法,属基础题.
2.C
【分析】
设圆锥的底面半径为,用将圆锥的底面积及侧面积分别表示即可得到答案.
【详解】
设圆锥的底面半径为,则高为,母线长 则,
, ,
故选:C .
3.D
【分析】
由已知条件知,圆锥的高和底面直径都为2,即可求圆锥的母线长,利用圆锥侧面积公式求面积即可.
【详解】
同底等高的圆锥和圆柱,圆柱的轴截面是边长为2的正方形,知:圆锥的高和底面直径都为2,
∴圆锥的母线长为:,
有侧面积.
故选:D
【点睛】
本题考查了圆锥侧面积的求法,结合圆柱、正方形的性质,并应用了圆锥侧面积公式,属于简单题.
4.A
【分析】
根据圆柱的侧面积公式计算即可.
【详解】
圆柱的母线长为,底面半径为,
则圆柱的侧面积为.
故选:A
【点睛】
本小题主要考查圆柱的侧面积公式,属于基础题.
5.A
【分析】
由三视图还原,可知该几何体是半圆柱,利用公式求其表面积即可.
【详解】
由三视图还原,可知该几何体是半圆柱,
半圆柱的底面半径为,高为2,
=
故选:A
【点睛】
本题主要考查了三视图--长对正、宽平齐、高相等得到实物图中的数据,由三视图还原实物图处理问题.还考查了表面积计算,属于基础题.
6.B
【分析】
该几何体的直观图是圆台,上底面是一个直径为2的圆,下底面是一个直径为4的圆,母线长是4,利用圆台的侧面积公式即得解.
【详解】
由三视图可知,正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,该几何体的直观图是圆台,上底面是一个直径为2的圆,下底面是一个直径为4的圆,母线长是4,
其圆台的侧面积是:.
故选:B.
【点睛】
本题主要考查三视图还原几何体,考查圆台的侧面积,意在考查学生对这些知识的理解掌握水平.
7.A
【分析】
该组合体由一个正四棱锥和一个长方体组成,由勾股定理可计算出正四棱锥的斜高,即可运用三角形的面积公式求出正四棱锥的侧面积,再求出长方体的侧面积和底面积,再求和即可.
【详解】
由题意,正四棱锥的斜高为,该组合体的表面积为.
故选:A
【点睛】
本题考查了组合体的表面积,求四棱锥的斜高是关键,考查了运算能力和空间想象能力,属于中档题.
8.A
【分析】
由已知得到圆锥的半径与母线长,再代入扇形面积公式求得圆锥侧展图面积.
【详解】
圆锥的侧面展开图是半径为,弧长为的扇形,其面积,所以圆锥的侧面展开图面积为.
【点睛】
本题考查求圆锥侧展图及扇形面积的基本运算.
9.A
【分析】
先根据圆台上、下底面面积分别是、,求出圆台上、下底面的半径,再由公式求圆台的侧面积.
【详解】
设圆台上、下底面的半径分别为,
由圆台上、下底面面积分别是、,则
所以
所以这个圆台的侧面积为
故选:A
【点睛】
本题考查求圆台的侧面积,直接利用公式,属于基础题.
10.
【分析】
利用圆锥的性质求出底面半径与母线长,再利用圆锥的侧面积计算公式即可得出.
【详解】
轴截面是边长为4等边三角形,
所以圆锥底面半径,
圆锥母线.
圆锥的侧面积.
故答案为:.
【点睛】
本题主要考查圆锥侧面积的求解,熟练掌握圆锥的性质及圆锥的侧面积的计算公式是解题的关键.
11.
【分析】
由题意可知,该半圆柱的侧视图为底边长为底面圆半径,高为的矩形,则根据侧视图的面积即可求得底面圆的半径.
【详解】
因为该半圆柱的高为,侧视图的面积为,则底面圆的半径为.
故答案为:.
【点睛】
本题考查与几何体的三视图有关的计算问题,属于简单题.
12.
【分析】
求出斜高,计算各面的面积,求和可得正四棱锥的表面积.
【详解】
如图所示,,则,,
故正四棱锥的表面积为.
故答案为:
【点睛】
本题考查了求正四棱锥的表面积,属于基础题.
13.2
【分析】
根据圆台的侧面积公式计算.
【详解】
由题意,解得.
故答案为:2.
【点睛】
本题考查圆台的侧面积公式,属于基础题.
14.
【分析】
首先求出四棱台上、下底面面积与侧面面积,然后求出表面积即可.
【详解】
如图,
在四棱台中,
过作,垂足为,
在中,,,
故,
所以,
故四棱台的侧面积,
所以四棱台的表面积.
【点睛】
本题考查了四棱台的表面积,属于基础题.
15.
【分析】
由圆柱、圆锥的底面面积比可得圆柱的底面半径和高分别为1、,进而求其表面积即可.
【详解】
由圆柱的底面积与圆锥的底面积之比为1:4,知:底面半径比为1:2,
即圆柱底面半径,若设圆柱的高为,则有,即,
∴由圆柱的表面积等于侧面积加上两底面的面积,
即:.
【点睛】
本题考查了圆柱的表面积计算,由圆锥内接圆柱及底面面积比求圆柱表面积,属于简单题.
16.160
【分析】
由于该直四棱柱的底面是菱形,所以求其中一个侧面的面积乘以4即可,由菱形其对角线垂直于勾股定理求得底面边长,再由矩形面积公式求得答案.
【详解】
如图,设底面对角线AC=a,BD=b,交点为O,对角线A1C=15,B1D=9,
∴a2+52=152,b2+52=92,∴a2=200,b2=56.
∵该直四棱柱的底面是菱形,
∴AB2====64,∴AB=8.
∴直四棱柱的侧面积S=4×8×5=160.
【点睛】
本题考查求直四棱柱的侧面积,属于基础题.
17.(1)5(2)80π
【分析】
(1)由圆台的侧面积公式与两底面圆的面积之和的关系构建方程,求得母线;
(2)由(1)可得圆台的母线,再由圆台的表面积的公式求得答案.
【详解】
(1)设圆台的母线长为l,则由题意得π(2+6)l=π×22+π×62,
∴8πl=40π,∴l=5,∴该圆台的母线长为5;
(2)由(1)可得圆台的表面积为S=π×(2+6)×5+π·22+π×62=40π+4π+36π=80π.
【点睛】
本题考查由圆台的性质求圆台的母线与表面积,属于基础题.
18.
【分析】
先求三个侧面的面积,再求解底面积,从而可得棱锥的表面积.
【详解】
∵正三棱锥的侧面都是等腰直角三角形,且底面边长为,
∴侧棱长等于,∴该棱锥的表面积.
【点睛】
本题主要考查三棱锥表面积的求解,表面积包含侧面积和底面积,侧面积可利用侧面积公式求解,侧重考查数学运算的核心素养.
