1.5.1平行关系的判定-北师大版高中数学必修二基础练习(Word含答案解析)
文档属性
| 名称 | 1.5.1平行关系的判定-北师大版高中数学必修二基础练习(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 15:05:57 | ||
图片预览


文档简介
1.5.1平行关系的判定基础练习题
一、单选题
1.如图所示,在正方体中,棱长为,、分别为和上的点,,则与平面的位置关系是( )
A.斜交 B.平行
C.垂直 D.在平面内
2.平面α与平面β平行的条件可以是( )
A.α内有无数条直线都与β平行
B.直线a∥α,a∥β,且直线a不在α内,也不在β内
C.α内的任何直线都与β平行
D.直线a在α内,直线b在β内,且a∥β,b∥α
3.已知平面,,则的一个充分条件是( )
A.平面内有无数条直线与平行 B.平面内有两条相交的直线与平行
C.平面,平行于同一条直线 D.平面,垂直于同一平面
4.如图,的边在平面内,是的中位线,则( )
A.与平面平行 B.与平面不平行
C.与平面可能平行 D.与平面可能相交
5.设α、β为两个不重合的平面,能使α//β成立的是( )
A.α内有无数条直线与β平行 B.α内有两条相交直线与β平行
C.α内有无数个点到β的距离相等 D.α、β垂直于同一平面
6.下列条件中,能判断两个平面平行的是( )
A.一个平面内的一条直线平行于另一个平面
B.一个平面内的两条直线平行于另一个平面
C.一个平面内的两条相交直线平行于另一个平面
D.一个平面内有无数条直线平行于另一个平面
二、解答题
7.如图所示,在底面为平行四边形的四棱锥中,,平面,且,点是的中点.求证:平面.
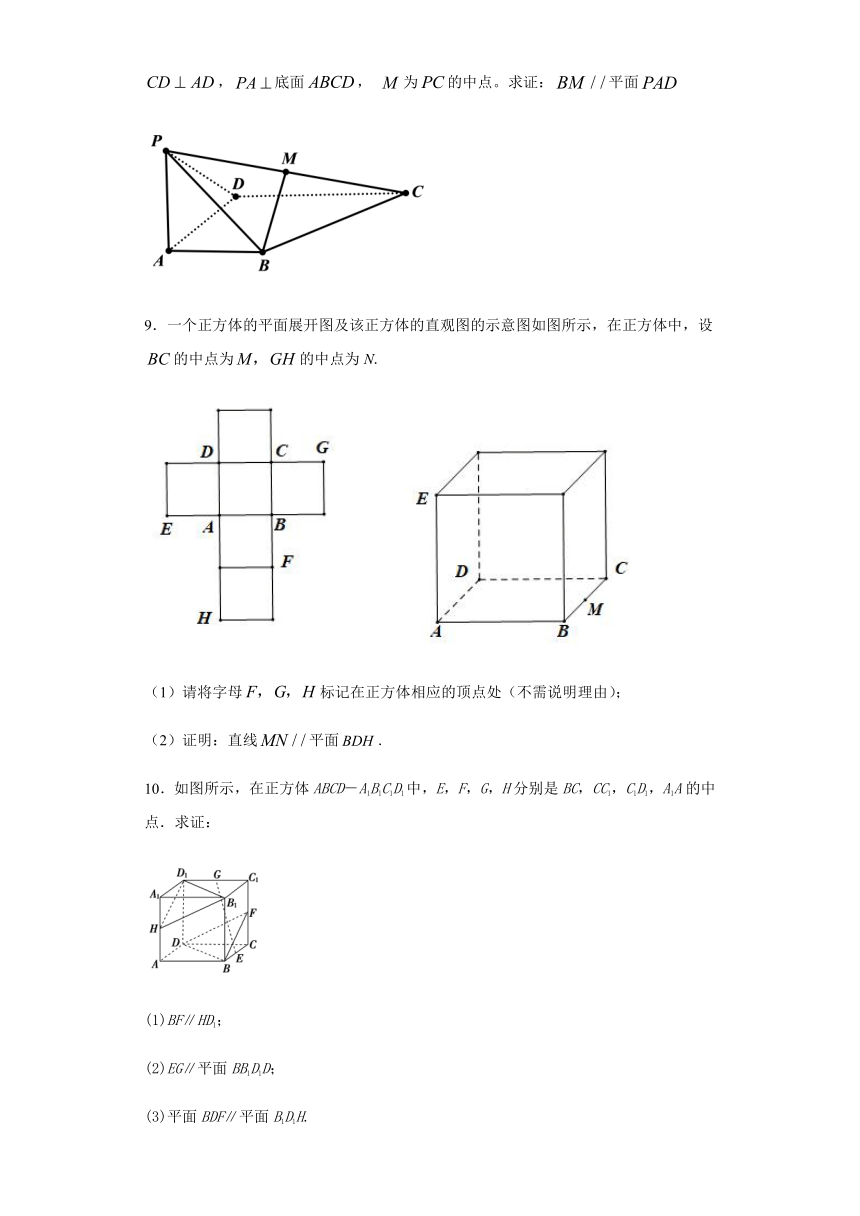
8.如图所示,在四棱锥中,,,,底面, 为的中点。求证:平面
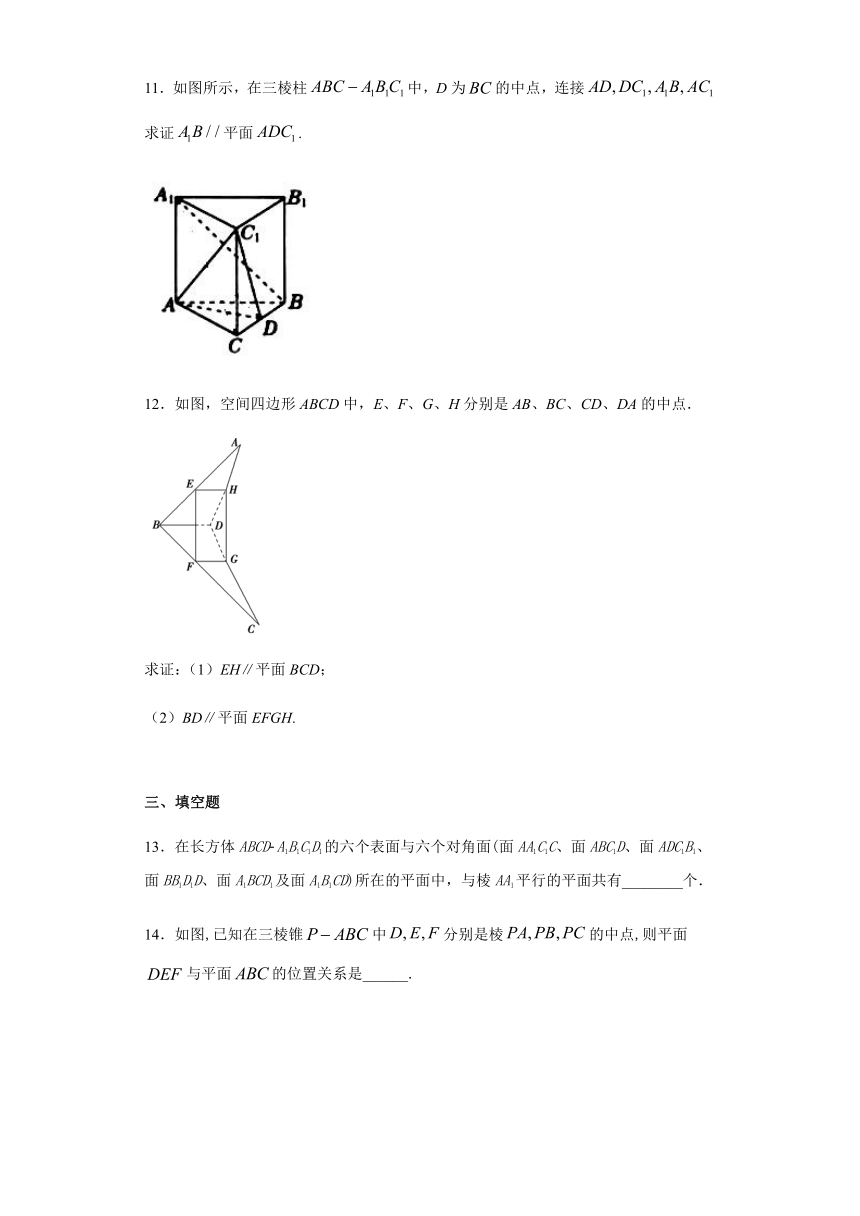
9.一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设的中点为的中点为N.
(1)请将字母标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线平面.
10.如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是BC,CC1,C1D1,A1A的中点.求证:
(1)BF∥HD1;
(2)EG∥平面BB1D1D;
(3)平面BDF∥平面B1D1H.
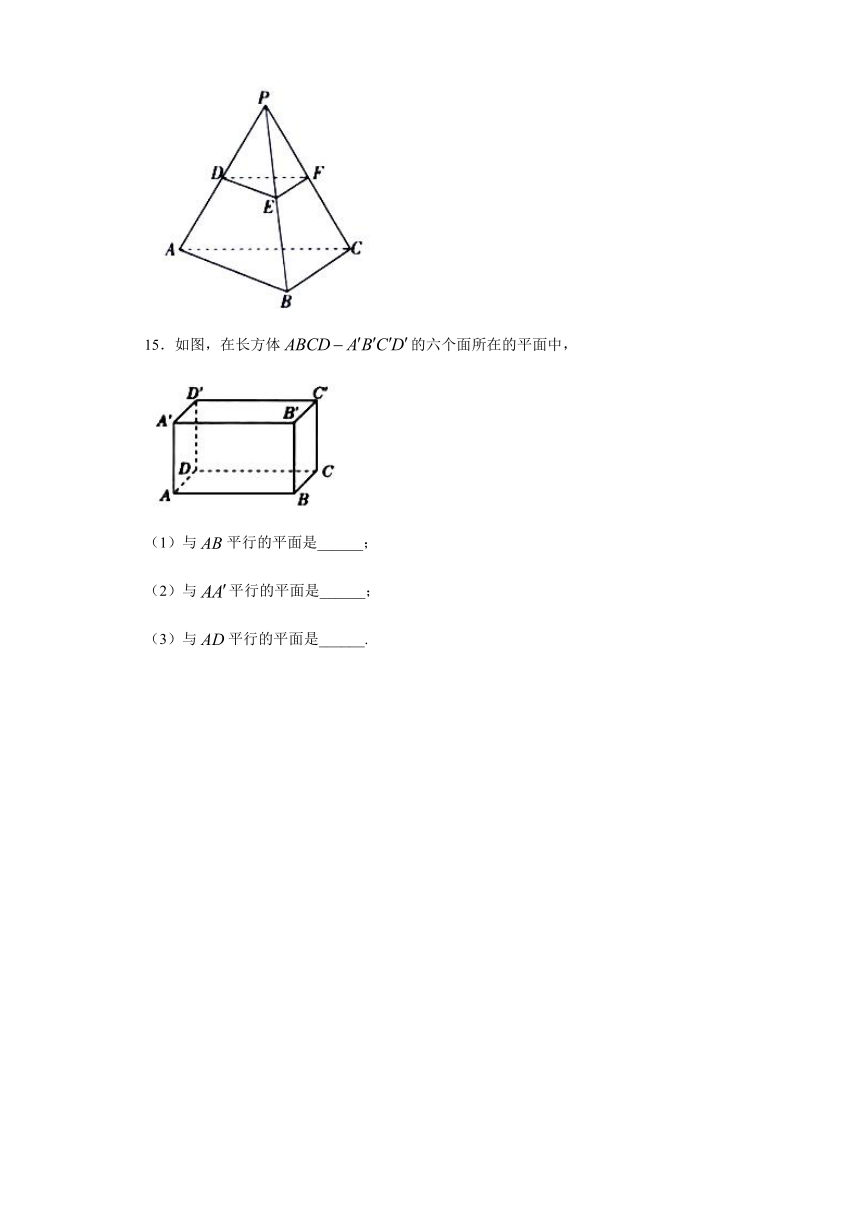
11.如图所示,在三棱柱中,D为的中点,连接求证平面.
12.如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:(1)EH∥平面BCD;
(2)BD∥平面EFGH.
三、填空题
13.在长方体ABCD?A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1CD)所在的平面中,与棱AA1平行的平面共有________个.
14.如图,已知在三棱锥中分别是棱的中点,则平面与平面的位置关系是______.
15.如图,在长方体的六个面所在的平面中,
(1)与平行的平面是______;
(2)与平行的平面是______;
(3)与平行的平面是______.
参考答案
1.B
【分析】
由于平面,为平面的一个法向量.因此只需证明向量与垂直即可.
【详解】
解:建立如图所示的空间直角坐标系,由于,
则,,.
又 平面
所以为平面的一个法向量.
因为,
所以,又 平面,
所以 平面.
故选B
.
【点睛】
本题考查线面平行的判定,在适当条件下,可以用向量法证明,只需证明该直线的一个方向向量与该平面的一个法向量垂直即可,要注意的是这两个向量必须用同一组基底来表示.
2.C
【分析】
根据面面平行的性质和判定定理进行判断即可
【详解】
对A,若α内的无数条直线都平行,平面α与平面β不一定平行,也可能相交,垂直,A错
对B,当直线平行于两平面交线时,符合命题叙述,但平面α与平面β相交,B错
对C,“α内的任何直线都与β平行”可等价转化为“α内的两条相交直线与β平行”,根据面面平行的判定定理,C正确
对D,当两平面相交,直线a,直线b都跟交线平行且符合命题叙述时,得不到平面α与平面β平行,D错
故选C
【点睛】
本题考查面面平行的判定:当两条相交直线与另一平面平行时,则过这两条交线的平面与另一平面平行
3.B
【分析】
根据充分条件的定义以及面面平行的判定定理即可得出正确.
【详解】
对于A,平面内有无数条直线与平行,若这些直线都平行,不一定能推出,A错误;
对于B,根据面面平行的判定定理可知B正确;
对于C,若平面,平行于同一条直线,则平面既可能平行,也可能相交,C错误;
对于D,若平面,垂直于同一平面,则平面既可能平行,也可能相交,D错误.
故选:B.
【点睛】
本题主要考查面面平行的判定定理的理解和应用,以及充分条件的定义的理解,属于容易题.
4.A
【分析】
根据线面平行的判定定理,即可得出结果.
【详解】
因为是的中位线,所以;
又,,
所以.
故选:A.
【点睛】
本题主要考查判断直线与平面是否平行,熟记线面平行的判定定理即可,属于常考题型.
5.B
【分析】
应用几何体特例,如立方体可排除相关选项;而由面面平行的判定可知B正确
【详解】
应用立方体,如下图所示:
选项A:α内有无数条直线可平行于l,即有无数条直线与β平行,但如上图α与β可相交于l,故A不一定能使α//β成立;
选项B:由面面平行的判定,可知B正确
选项C:在α内有一条直线平行于l,则在α内有无数个点到β的距离相等,但如上图α与β可相交于l,故C不一定能使α//β成立;
选项D:如图α⊥γ,β⊥γ,但α与β可相交于l,故D不一定能使α//β成立;
故选:B
【点睛】
本题考查了面面平行的判定,应用特殊与一般的思想排除选项,属于简单题
6.C
【分析】
根据面面平行的判定定理或定义可得出结论.
【详解】
根据面面平行的定义可知,若两个平面没有公共点,则这两个平面平行,则一个平面内所有直线都与另一个平面没有公共点,则这两个平面平行.
由面面平行的判定定理可知,一个平面内两条相交直线与另一个平面平行,则这两个平面平行.
故选:C.
【点睛】
本题考查面面平行的判断,一般利用面面平行的定义或判定定理来判断,考查对面面平行的定义和判定定理的理解,属于基础题.
7.证明见解析
【分析】
根据图像,连接,与相交与,连接,是平行四边形,是的中点,根据中位线的性质即可得证.
【详解】
如图,
连接,与相交与,连接,
∵是平行四边形,
∴是的中点,
又是的中点,
∴,
又平面,平面,
∴平面.
8.证明见解析.
【分析】
取的中点,连接,由三角形的中位线定理可得∥,,而已知∥,,从而得∥,,所以四边形为平行四边形,从而得,再利用线面平行的判定定理可证明
【详解】
证明:取的中点,连接
因为为的中点,
所以∥,,
因为∥,,
所以∥,,
所以四边形为平行四边形,所以,
又因为平面,平面,
所以平面.
9.(1)见解析(2)证明见解析
【分析】
(1)根据正方体的平面展开图与原图的对应关系,标出点的坐标.
(2)通过构造平行四边形,证得与平面内的一条直线平行,由此证得直线平面.
【详解】
(1)解:点的位置如图所示.
(2)如图,连接,设O为的中点,连接.
因为分别是的中点,
所以,且,
,且,
所以,.
所以四边形是平行四边形,从而.
又平面,平面,
所以平面.
【点睛】
本小题主要考查线面平行的证明,考查正方体的展开图,考查空间想象能力和逻辑推理能力,属于基础题.
10.(1) 见解析;(2) 见解析;(3)见解析.
【分析】
(1)取BB1的中点M,连接HM、MC1,四边则HMC1D1是平行四边形,即可证明BF∥HD1;(2)取B1D1的中点O,易证四边形BEGO为平行四边形,故有OB∥GE,从而证明EG∥平面BB1D1D.(3)由正方体得BD∥B1D1,由四边形HBFD1是平行四边形,可得 HD1∥BF,可证 平面BDF∥平面B1D1H.
【详解】
(1)取BB1的中点M,连接HM、MC1,四边则HMC1D1是平行四边形,∴HD1∥MC1.
又∵MC1∥BF,∴BF∥HD1.
(2)取BD的中点O,连接EO、D1O,则OE∥,OE=.又D1G∥DC,D1G=DC,
∴OE∥D1G,OE=D1G,∴四边形OEGD1是平行四边形,∴GE∥D1O.
又D1O?平面BB1D1D,∴EG∥平面BB1D1D.
(3)由(1)知D1H∥BF,又BD∥B1D1,B1D1、HD1?平面HB1D1,BF、BD?平面BDF,且B1D1∩HD1=D1,DB∩BF=B,∴平面BDF∥平面B1D1H.
【点睛】
本题考查了面面平行、线面平行的方法,直线与平面平行的判定、性质的应用,属于基础题.
11.见解析
【分析】
要证平面,只要证与平面内某条直线平行即可.因为D是边的中点,所以考虑从中位线入手,在平面内找与平行的直线,再结合线面平行的判定定理,证得平面.
【详解】
如图,连接,设,连接.
由题意知四边形是平行四边形,
所以O是的中点.
又D是的中点,所以是的中位线,即.
又平面,平面,所以平面.
【点睛】
本小题主要考查线面平行的证明,考查空间想象能力和逻辑推理能力,属于基础题.
12.(1)见解析(2)见解析
【分析】
(1)推导出EH∥BD,由此能证明EH∥平面BCD;
(2)由BD∥EH,由此能证明BD∥平面EFGH.
【详解】
(1)∵EH为△ABD的中位线,
∴EH∥BD.
∵EH?平面BCD,BD?平面BCD,
∴EH∥平面BCD;
(2)∵FG为△CBD的中位线,
∴FG∥BD,
∴FG∥EH,
∴E、F、G、H四点共面,
∵BD∥EH,BD?平面EFGH,EH?平面EFGH,
∴BD∥平面EFGH.
【点睛】
本题考查线面平行的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查化归与转化思想,是中档题.
13.3
【解析】
画出图形如下图所示,
结合图形可得平面,平面,平面.所以棱AA1平行的平面共有3个.
答案:3
14.平行
【分析】
由中点得到三角形的中位线,进而得到线线平行,然后再结合面面平行的判定定理证明面面平行.
【详解】
在中,因为分别是,的中点,所以.
又平面,平面,
所以平面.
同理,可证平面.
又,,平面,
所以平面平面.
故答案为:平行
【点睛】
本题考查了面面平行的判定证明,在证明面面平行时的方法:有中点找中点,构造三角形中位线或平行四边形,得到线线平行,由线面平行的判定定理证明线面平行,再由面面平行判定定理证明面面平行.所以在解题时找中点很重要.
15.平面,平面 平面,平面 平面,平面
【分析】
(1)根据线面平行的判定定理填写出正确结论.
(2)根据线面平行的判定定理填写出正确结论.
(3)根据线面平行的判定定理填写出正确结论.
【详解】
(1)由于,平面,平面,所以平面.同理证得平面.
(2)由于,平面,平面,所以平面.同理证得平面.
(3)由于,平面,平面,所以平面.同理证得平面.
故答案为:(1). 平面,平面;(2). 平面,平面; (3). 平面,平面.
【点睛】
本小题主要考查线面平行的判定定理,属于基础题.
一、单选题
1.如图所示,在正方体中,棱长为,、分别为和上的点,,则与平面的位置关系是( )
A.斜交 B.平行
C.垂直 D.在平面内
2.平面α与平面β平行的条件可以是( )
A.α内有无数条直线都与β平行
B.直线a∥α,a∥β,且直线a不在α内,也不在β内
C.α内的任何直线都与β平行
D.直线a在α内,直线b在β内,且a∥β,b∥α
3.已知平面,,则的一个充分条件是( )
A.平面内有无数条直线与平行 B.平面内有两条相交的直线与平行
C.平面,平行于同一条直线 D.平面,垂直于同一平面
4.如图,的边在平面内,是的中位线,则( )
A.与平面平行 B.与平面不平行
C.与平面可能平行 D.与平面可能相交
5.设α、β为两个不重合的平面,能使α//β成立的是( )
A.α内有无数条直线与β平行 B.α内有两条相交直线与β平行
C.α内有无数个点到β的距离相等 D.α、β垂直于同一平面
6.下列条件中,能判断两个平面平行的是( )
A.一个平面内的一条直线平行于另一个平面
B.一个平面内的两条直线平行于另一个平面
C.一个平面内的两条相交直线平行于另一个平面
D.一个平面内有无数条直线平行于另一个平面
二、解答题
7.如图所示,在底面为平行四边形的四棱锥中,,平面,且,点是的中点.求证:平面.
8.如图所示,在四棱锥中,,,,底面, 为的中点。求证:平面
9.一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设的中点为的中点为N.
(1)请将字母标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线平面.
10.如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是BC,CC1,C1D1,A1A的中点.求证:
(1)BF∥HD1;
(2)EG∥平面BB1D1D;
(3)平面BDF∥平面B1D1H.
11.如图所示,在三棱柱中,D为的中点,连接求证平面.
12.如图,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:(1)EH∥平面BCD;
(2)BD∥平面EFGH.
三、填空题
13.在长方体ABCD?A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1CD)所在的平面中,与棱AA1平行的平面共有________个.
14.如图,已知在三棱锥中分别是棱的中点,则平面与平面的位置关系是______.
15.如图,在长方体的六个面所在的平面中,
(1)与平行的平面是______;
(2)与平行的平面是______;
(3)与平行的平面是______.
参考答案
1.B
【分析】
由于平面,为平面的一个法向量.因此只需证明向量与垂直即可.
【详解】
解:建立如图所示的空间直角坐标系,由于,
则,,.
又 平面
所以为平面的一个法向量.
因为,
所以,又 平面,
所以 平面.
故选B
.
【点睛】
本题考查线面平行的判定,在适当条件下,可以用向量法证明,只需证明该直线的一个方向向量与该平面的一个法向量垂直即可,要注意的是这两个向量必须用同一组基底来表示.
2.C
【分析】
根据面面平行的性质和判定定理进行判断即可
【详解】
对A,若α内的无数条直线都平行,平面α与平面β不一定平行,也可能相交,垂直,A错
对B,当直线平行于两平面交线时,符合命题叙述,但平面α与平面β相交,B错
对C,“α内的任何直线都与β平行”可等价转化为“α内的两条相交直线与β平行”,根据面面平行的判定定理,C正确
对D,当两平面相交,直线a,直线b都跟交线平行且符合命题叙述时,得不到平面α与平面β平行,D错
故选C
【点睛】
本题考查面面平行的判定:当两条相交直线与另一平面平行时,则过这两条交线的平面与另一平面平行
3.B
【分析】
根据充分条件的定义以及面面平行的判定定理即可得出正确.
【详解】
对于A,平面内有无数条直线与平行,若这些直线都平行,不一定能推出,A错误;
对于B,根据面面平行的判定定理可知B正确;
对于C,若平面,平行于同一条直线,则平面既可能平行,也可能相交,C错误;
对于D,若平面,垂直于同一平面,则平面既可能平行,也可能相交,D错误.
故选:B.
【点睛】
本题主要考查面面平行的判定定理的理解和应用,以及充分条件的定义的理解,属于容易题.
4.A
【分析】
根据线面平行的判定定理,即可得出结果.
【详解】
因为是的中位线,所以;
又,,
所以.
故选:A.
【点睛】
本题主要考查判断直线与平面是否平行,熟记线面平行的判定定理即可,属于常考题型.
5.B
【分析】
应用几何体特例,如立方体可排除相关选项;而由面面平行的判定可知B正确
【详解】
应用立方体,如下图所示:
选项A:α内有无数条直线可平行于l,即有无数条直线与β平行,但如上图α与β可相交于l,故A不一定能使α//β成立;
选项B:由面面平行的判定,可知B正确
选项C:在α内有一条直线平行于l,则在α内有无数个点到β的距离相等,但如上图α与β可相交于l,故C不一定能使α//β成立;
选项D:如图α⊥γ,β⊥γ,但α与β可相交于l,故D不一定能使α//β成立;
故选:B
【点睛】
本题考查了面面平行的判定,应用特殊与一般的思想排除选项,属于简单题
6.C
【分析】
根据面面平行的判定定理或定义可得出结论.
【详解】
根据面面平行的定义可知,若两个平面没有公共点,则这两个平面平行,则一个平面内所有直线都与另一个平面没有公共点,则这两个平面平行.
由面面平行的判定定理可知,一个平面内两条相交直线与另一个平面平行,则这两个平面平行.
故选:C.
【点睛】
本题考查面面平行的判断,一般利用面面平行的定义或判定定理来判断,考查对面面平行的定义和判定定理的理解,属于基础题.
7.证明见解析
【分析】
根据图像,连接,与相交与,连接,是平行四边形,是的中点,根据中位线的性质即可得证.
【详解】
如图,
连接,与相交与,连接,
∵是平行四边形,
∴是的中点,
又是的中点,
∴,
又平面,平面,
∴平面.
8.证明见解析.
【分析】
取的中点,连接,由三角形的中位线定理可得∥,,而已知∥,,从而得∥,,所以四边形为平行四边形,从而得,再利用线面平行的判定定理可证明
【详解】
证明:取的中点,连接
因为为的中点,
所以∥,,
因为∥,,
所以∥,,
所以四边形为平行四边形,所以,
又因为平面,平面,
所以平面.
9.(1)见解析(2)证明见解析
【分析】
(1)根据正方体的平面展开图与原图的对应关系,标出点的坐标.
(2)通过构造平行四边形,证得与平面内的一条直线平行,由此证得直线平面.
【详解】
(1)解:点的位置如图所示.
(2)如图,连接,设O为的中点,连接.
因为分别是的中点,
所以,且,
,且,
所以,.
所以四边形是平行四边形,从而.
又平面,平面,
所以平面.
【点睛】
本小题主要考查线面平行的证明,考查正方体的展开图,考查空间想象能力和逻辑推理能力,属于基础题.
10.(1) 见解析;(2) 见解析;(3)见解析.
【分析】
(1)取BB1的中点M,连接HM、MC1,四边则HMC1D1是平行四边形,即可证明BF∥HD1;(2)取B1D1的中点O,易证四边形BEGO为平行四边形,故有OB∥GE,从而证明EG∥平面BB1D1D.(3)由正方体得BD∥B1D1,由四边形HBFD1是平行四边形,可得 HD1∥BF,可证 平面BDF∥平面B1D1H.
【详解】
(1)取BB1的中点M,连接HM、MC1,四边则HMC1D1是平行四边形,∴HD1∥MC1.
又∵MC1∥BF,∴BF∥HD1.
(2)取BD的中点O,连接EO、D1O,则OE∥,OE=.又D1G∥DC,D1G=DC,
∴OE∥D1G,OE=D1G,∴四边形OEGD1是平行四边形,∴GE∥D1O.
又D1O?平面BB1D1D,∴EG∥平面BB1D1D.
(3)由(1)知D1H∥BF,又BD∥B1D1,B1D1、HD1?平面HB1D1,BF、BD?平面BDF,且B1D1∩HD1=D1,DB∩BF=B,∴平面BDF∥平面B1D1H.
【点睛】
本题考查了面面平行、线面平行的方法,直线与平面平行的判定、性质的应用,属于基础题.
11.见解析
【分析】
要证平面,只要证与平面内某条直线平行即可.因为D是边的中点,所以考虑从中位线入手,在平面内找与平行的直线,再结合线面平行的判定定理,证得平面.
【详解】
如图,连接,设,连接.
由题意知四边形是平行四边形,
所以O是的中点.
又D是的中点,所以是的中位线,即.
又平面,平面,所以平面.
【点睛】
本小题主要考查线面平行的证明,考查空间想象能力和逻辑推理能力,属于基础题.
12.(1)见解析(2)见解析
【分析】
(1)推导出EH∥BD,由此能证明EH∥平面BCD;
(2)由BD∥EH,由此能证明BD∥平面EFGH.
【详解】
(1)∵EH为△ABD的中位线,
∴EH∥BD.
∵EH?平面BCD,BD?平面BCD,
∴EH∥平面BCD;
(2)∵FG为△CBD的中位线,
∴FG∥BD,
∴FG∥EH,
∴E、F、G、H四点共面,
∵BD∥EH,BD?平面EFGH,EH?平面EFGH,
∴BD∥平面EFGH.
【点睛】
本题考查线面平行的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查化归与转化思想,是中档题.
13.3
【解析】
画出图形如下图所示,
结合图形可得平面,平面,平面.所以棱AA1平行的平面共有3个.
答案:3
14.平行
【分析】
由中点得到三角形的中位线,进而得到线线平行,然后再结合面面平行的判定定理证明面面平行.
【详解】
在中,因为分别是,的中点,所以.
又平面,平面,
所以平面.
同理,可证平面.
又,,平面,
所以平面平面.
故答案为:平行
【点睛】
本题考查了面面平行的判定证明,在证明面面平行时的方法:有中点找中点,构造三角形中位线或平行四边形,得到线线平行,由线面平行的判定定理证明线面平行,再由面面平行判定定理证明面面平行.所以在解题时找中点很重要.
15.平面,平面 平面,平面 平面,平面
【分析】
(1)根据线面平行的判定定理填写出正确结论.
(2)根据线面平行的判定定理填写出正确结论.
(3)根据线面平行的判定定理填写出正确结论.
【详解】
(1)由于,平面,平面,所以平面.同理证得平面.
(2)由于,平面,平面,所以平面.同理证得平面.
(3)由于,平面,平面,所以平面.同理证得平面.
故答案为:(1). 平面,平面;(2). 平面,平面; (3). 平面,平面.
【点睛】
本小题主要考查线面平行的判定定理,属于基础题.
