安徽省铜陵市铜官区2020-2021学年七年级下学期期末考试数学试题(Word版含答案)
文档属性
| 名称 | 安徽省铜陵市铜官区2020-2021学年七年级下学期期末考试数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 131.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 08:09:26 | ||
图片预览



文档简介
铜陵市铜官区2020-2021学年度第二学期期末质量监测
七年级数学试卷
(考试时间:100分钟,满分:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1、下列哪个图形可以通过平移得到的( )
A.
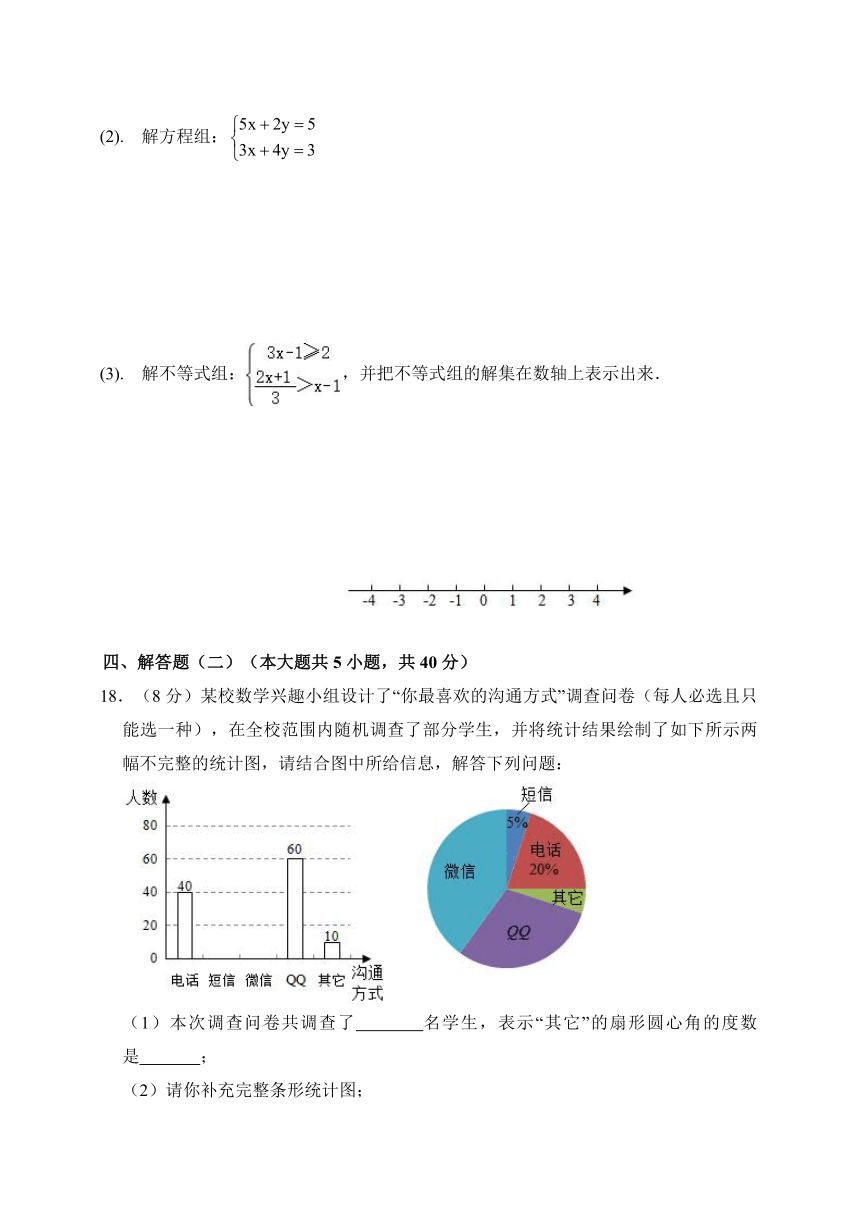
B.
C.
D.
2、下列算式正确的是( )
A.
B.
C.
D.
3、若A(2m﹣4,6﹣2m)在第二象限,则m的取值范围是( )
A.m<2
B.2<m<3
C.m>3
D.m<3
4、已知实数a,b满足:(a﹣b+3)2
+
=0,则等于( )
A.65
B.64
C.
63
D.62
如右图,平面内,已知AB∥DE,∠ABC=130°,
∠CDE=110°,则∠BCD的度数为( )
A.50°
B.60
C.70°
D.80°
6、关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值是( )
A.﹣
B.
C.
D.﹣
7、下列调查适合抽样调查的是(
)
A.检查小明同学昨天作文的错别字
B.检查“天宫二号”飞行器各部件质量
C.调查某班同学观看《最强大脑》的人数
D.对长江流域水污染情况进行调查
8、已知数轴上点A、B分别表示,,若点C也在同一数轴上,且AC=2AB,则点C所表示的数为( )
A.3﹣2
B.2﹣
C.+或3﹣2
D.3﹣2或2﹣
9、若关于x的不等式>0的解集是x<,则关于x的不等式>的解集是( )
A.x<
B.x<
C.x>
D.x>
10、如右图,AB∥CD,PG平分∠EPF,∠A+∠AHP=180°,下列结论:
①CD∥PH;②∠BEP+∠DFP=2∠EPG;③∠FPH=∠GPH;④∠A+∠AGP+∠DFP﹣∠FPG=180°;⑤若∠BEP>∠DFP,则=2,
其中正确结论的个数是( )
A.2个
B.3个
C.4个
D.5个
二、填空题(本大题共6小题,每小题3分,共18分)
11、在实数①,②,③3.14,④,⑤中,是无理数的有
;(填写
序号)
12、若(m﹣1)x|m|+3>0是关于x的一元一次不等式,则m=
.
13、若不等式组的解集是x>2,则m的取值范围是
.
14、同一平面内,已知∠α两边与∠β的两边分别平行,若∠α=60°,则∠β的度数为
.
15、现有一条长度为359mm的铜管料,把它锯成长度分别为39mm和29mm的两种不同规格的小铜管,(要求没有余料).每锯一次损耗1mm的铜管料.为了使铜管料损耗最少,应分别锯成39mm的小铜管______段,29mm的小铜管______段.
16、如右下图所示,在平面直角坐标系中,点A在x轴的正半轴上,直线BC经过原点O,,AD⊥BC于
D,若A(5,0),B(m,2),C(n,-4),则AD·BC=???.
三、解答题(一)
17.计算、解方程组、不等式组(共12分):
(1).
计算:
|3﹣|+﹣+.
(2).
解方程组:
(3).
解不等式组:,并把不等式组的解集在数轴上表示出来.
四、解答题(二)(本大题共5小题,共40分)
18.(8分)某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只能选一种),在全校范围内随机调查了部分学生,并将统计结果绘制了如下所示两幅不完整的统计图,请结合图中所给信息,解答下列问题:
(1)本次调查问卷共调查了
名学生,表示“其它”的扇形圆心角的度数是
;
(2)请你补充完整条形统计图;
(3)如果该校有1000名学生,请估计该校最喜欢用“微信”进行沟通的学生约有多少名?
(7分)解方程组时,小强正确解得,而小刚只看错了c,
解得
(1).
小刚把c错看成了什么数?
(2).
求的值.
20.(8分)甲,乙两人在同一药店购买100只医用一次性口罩和30只KN
95口罩,共用了660元;购买50只医用一次性口罩和20只KN
95口罩,共用了420元.
(1)医用一次性口罩和KN
95口罩的单价分别是多少元?
(2)若丙也来该药店购买,购买医用一次性口罩的数量比购买KN
95口罩数量的2倍少4只,且购买两种口罩的总费用不超过500元,求丙最多购买多少只KN
95口罩?
21.(8分)如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由.
(9分)【问题情境】:
我们知道:在平面直角坐标系中有不重合的两点A(x1,y1)和点B(x2,y2),若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|.
【拓展】
现在,若规定:平面直角坐标系中任意不重合的两点M(x1,y1)、N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|.例如:图中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5,
【应用】
解决下列问题:
(1)已知点E(3,2),点F(1,﹣2),求d(E,F)的值.
(2)已知点E(3,1),H(﹣1,n),若d(E,H)=6,直接写出n的值;
(3)已知点P(3,4),点Q在y轴上,O为坐标系原点,且△OPQ的面积是4.5,求d(P,Q)的值.
铜陵市铜官区2020-2021学年度第二学期期末质量监测
七年级数学参考答案
一、选择题(每题3分)
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
A
C
B
B
D
D
B
C
二、填空题(每题3分)
题号
11
12
13
14
15
16
答案
②⑤
-1
m≤2
60°或120°
6,
4
30
三、解答题
17.(1).
解:原式=﹣3﹣3﹣+5--------------------------------------2分
=﹣1.
---------------------------------4分
(2)解方程组
解:①×2﹣②得:7x=7,
解得:x=1,
-----------------------------------2分
把x=1代入①得:5+2y=5,
解得:y=0,
-----------------------------------3分
方程组的解为:.-----------------------------------4分
(用代入法正确解方程组不扣分)
,
解:由①得:x≥1,
由②得:x<4,
则不等式组的解集为1≤x<4,-----------------------------------3分
---------------------------------4分
解:(1)200人;
18°;-----------------------------------4分
短信的人数为:200×5%=10人,
微信人数为:200﹣40﹣10﹣60﹣10=80人
(图略)-----------------------6分
(3)1000×=400人,-----------------------------------7分
答:该校有1000名学生喜欢用“微信”进行沟通的学生约有400名.---------------------8分
解:(1)把,代入得
解得
----------------------------2分
答
小刚把c错看成了-7.----------------------------3分
.由题意得解得
所以a,b的值分别为1,2.
-------------7分
20.解:(1)设一只医用一次性口罩的售价为x元,一只KN95口罩的售价为y元,
由题意,得:,
-------------------------3分
解得,
-------------------------4分
答:一只医用一次性口罩的售价为1.2元,一只KN95口罩的售价为18元;----------5分
(2)设丙购买m只KN95口罩,则购买医用一次性口罩为(2m﹣4)只,
由题意得,1.2(2m﹣4)+18m≤500,
-----------------------6分
解得m≤24,∵m整数,∴m的最大值为24,----------7分
答:丙最多购买24只KN
95口罩.
-------------------------8分
21.
(1)解:∵AD∥BC,∠A=70°
∴∠
ABC=180°-∠
A=110°--------------------------------------2分
∵BE平分∠
ABC
∴∠
ABE=∠
ABC=55°-----------------------------------------3分
(2)证明:DF∥
BE-------------------------------------------------------4分
∵AB∥
CD
∴∠
A+∠
ADC=180°,∠
2=∠
AFD
∵AD∥
BC
∴∠
A+∠
ABC=180°
∴∠ADC=∠ABC-----------------------------------------------6分
∵∠
1=∠
2=∠ADC,∠
ABE=∠
ABC
∴∠
2=∠
ABE
∴∠AFD
=∠
ABE
∴DF∥
BE-------------------------------------------8分
22.解:(1)∵点E(3,2),点F(1,﹣2),
∴d(E,F)=|3﹣1|+|2﹣(﹣2)|=6.------------------------3分
(2)n=-1
或3
------------------------5分
(3)如图,设Q(0,m).
由题意,?|m|?2=4.5,
解得m=±3,
∴Q(0,3)或(0,﹣3),------------------------------7分
当Q(0,3)时,d(P,Q)=|3﹣0|+|4﹣3|=4,
当Q(0,﹣4)时,d(P,Q)=|3﹣0|+|4﹣(﹣3)|=10,
∴d(P,Q)=4或10.
-------------------------------9分
七年级数学试卷
(考试时间:100分钟,满分:100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1、下列哪个图形可以通过平移得到的( )
A.
B.
C.
D.
2、下列算式正确的是( )
A.
B.
C.
D.
3、若A(2m﹣4,6﹣2m)在第二象限,则m的取值范围是( )
A.m<2
B.2<m<3
C.m>3
D.m<3
4、已知实数a,b满足:(a﹣b+3)2
+
=0,则等于( )
A.65
B.64
C.
63
D.62
如右图,平面内,已知AB∥DE,∠ABC=130°,
∠CDE=110°,则∠BCD的度数为( )
A.50°
B.60
C.70°
D.80°
6、关于x,y的二元一次方程组的解也是二元一次方程2x+3y=6的解,则k的值是( )
A.﹣
B.
C.
D.﹣
7、下列调查适合抽样调查的是(
)
A.检查小明同学昨天作文的错别字
B.检查“天宫二号”飞行器各部件质量
C.调查某班同学观看《最强大脑》的人数
D.对长江流域水污染情况进行调查
8、已知数轴上点A、B分别表示,,若点C也在同一数轴上,且AC=2AB,则点C所表示的数为( )
A.3﹣2
B.2﹣
C.+或3﹣2
D.3﹣2或2﹣
9、若关于x的不等式>0的解集是x<,则关于x的不等式>的解集是( )
A.x<
B.x<
C.x>
D.x>
10、如右图,AB∥CD,PG平分∠EPF,∠A+∠AHP=180°,下列结论:
①CD∥PH;②∠BEP+∠DFP=2∠EPG;③∠FPH=∠GPH;④∠A+∠AGP+∠DFP﹣∠FPG=180°;⑤若∠BEP>∠DFP,则=2,
其中正确结论的个数是( )
A.2个
B.3个
C.4个
D.5个
二、填空题(本大题共6小题,每小题3分,共18分)
11、在实数①,②,③3.14,④,⑤中,是无理数的有
;(填写
序号)
12、若(m﹣1)x|m|+3>0是关于x的一元一次不等式,则m=
.
13、若不等式组的解集是x>2,则m的取值范围是
.
14、同一平面内,已知∠α两边与∠β的两边分别平行,若∠α=60°,则∠β的度数为
.
15、现有一条长度为359mm的铜管料,把它锯成长度分别为39mm和29mm的两种不同规格的小铜管,(要求没有余料).每锯一次损耗1mm的铜管料.为了使铜管料损耗最少,应分别锯成39mm的小铜管______段,29mm的小铜管______段.
16、如右下图所示,在平面直角坐标系中,点A在x轴的正半轴上,直线BC经过原点O,,AD⊥BC于
D,若A(5,0),B(m,2),C(n,-4),则AD·BC=???.
三、解答题(一)
17.计算、解方程组、不等式组(共12分):
(1).
计算:
|3﹣|+﹣+.
(2).
解方程组:
(3).
解不等式组:,并把不等式组的解集在数轴上表示出来.
四、解答题(二)(本大题共5小题,共40分)
18.(8分)某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只能选一种),在全校范围内随机调查了部分学生,并将统计结果绘制了如下所示两幅不完整的统计图,请结合图中所给信息,解答下列问题:
(1)本次调查问卷共调查了
名学生,表示“其它”的扇形圆心角的度数是
;
(2)请你补充完整条形统计图;
(3)如果该校有1000名学生,请估计该校最喜欢用“微信”进行沟通的学生约有多少名?
(7分)解方程组时,小强正确解得,而小刚只看错了c,
解得
(1).
小刚把c错看成了什么数?
(2).
求的值.
20.(8分)甲,乙两人在同一药店购买100只医用一次性口罩和30只KN
95口罩,共用了660元;购买50只医用一次性口罩和20只KN
95口罩,共用了420元.
(1)医用一次性口罩和KN
95口罩的单价分别是多少元?
(2)若丙也来该药店购买,购买医用一次性口罩的数量比购买KN
95口罩数量的2倍少4只,且购买两种口罩的总费用不超过500元,求丙最多购买多少只KN
95口罩?
21.(8分)如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由.
(9分)【问题情境】:
我们知道:在平面直角坐标系中有不重合的两点A(x1,y1)和点B(x2,y2),若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|.
【拓展】
现在,若规定:平面直角坐标系中任意不重合的两点M(x1,y1)、N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|.例如:图中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5,
【应用】
解决下列问题:
(1)已知点E(3,2),点F(1,﹣2),求d(E,F)的值.
(2)已知点E(3,1),H(﹣1,n),若d(E,H)=6,直接写出n的值;
(3)已知点P(3,4),点Q在y轴上,O为坐标系原点,且△OPQ的面积是4.5,求d(P,Q)的值.
铜陵市铜官区2020-2021学年度第二学期期末质量监测
七年级数学参考答案
一、选择题(每题3分)
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
A
C
B
B
D
D
B
C
二、填空题(每题3分)
题号
11
12
13
14
15
16
答案
②⑤
-1
m≤2
60°或120°
6,
4
30
三、解答题
17.(1).
解:原式=﹣3﹣3﹣+5--------------------------------------2分
=﹣1.
---------------------------------4分
(2)解方程组
解:①×2﹣②得:7x=7,
解得:x=1,
-----------------------------------2分
把x=1代入①得:5+2y=5,
解得:y=0,
-----------------------------------3分
方程组的解为:.-----------------------------------4分
(用代入法正确解方程组不扣分)
,
解:由①得:x≥1,
由②得:x<4,
则不等式组的解集为1≤x<4,-----------------------------------3分
---------------------------------4分
解:(1)200人;
18°;-----------------------------------4分
短信的人数为:200×5%=10人,
微信人数为:200﹣40﹣10﹣60﹣10=80人
(图略)-----------------------6分
(3)1000×=400人,-----------------------------------7分
答:该校有1000名学生喜欢用“微信”进行沟通的学生约有400名.---------------------8分
解:(1)把,代入得
解得
----------------------------2分
答
小刚把c错看成了-7.----------------------------3分
.由题意得解得
所以a,b的值分别为1,2.
-------------7分
20.解:(1)设一只医用一次性口罩的售价为x元,一只KN95口罩的售价为y元,
由题意,得:,
-------------------------3分
解得,
-------------------------4分
答:一只医用一次性口罩的售价为1.2元,一只KN95口罩的售价为18元;----------5分
(2)设丙购买m只KN95口罩,则购买医用一次性口罩为(2m﹣4)只,
由题意得,1.2(2m﹣4)+18m≤500,
-----------------------6分
解得m≤24,∵m整数,∴m的最大值为24,----------7分
答:丙最多购买24只KN
95口罩.
-------------------------8分
21.
(1)解:∵AD∥BC,∠A=70°
∴∠
ABC=180°-∠
A=110°--------------------------------------2分
∵BE平分∠
ABC
∴∠
ABE=∠
ABC=55°-----------------------------------------3分
(2)证明:DF∥
BE-------------------------------------------------------4分
∵AB∥
CD
∴∠
A+∠
ADC=180°,∠
2=∠
AFD
∵AD∥
BC
∴∠
A+∠
ABC=180°
∴∠ADC=∠ABC-----------------------------------------------6分
∵∠
1=∠
2=∠ADC,∠
ABE=∠
ABC
∴∠
2=∠
ABE
∴∠AFD
=∠
ABE
∴DF∥
BE-------------------------------------------8分
22.解:(1)∵点E(3,2),点F(1,﹣2),
∴d(E,F)=|3﹣1|+|2﹣(﹣2)|=6.------------------------3分
(2)n=-1
或3
------------------------5分
(3)如图,设Q(0,m).
由题意,?|m|?2=4.5,
解得m=±3,
∴Q(0,3)或(0,﹣3),------------------------------7分
当Q(0,3)时,d(P,Q)=|3﹣0|+|4﹣3|=4,
当Q(0,﹣4)时,d(P,Q)=|3﹣0|+|4﹣(﹣3)|=10,
∴d(P,Q)=4或10.
-------------------------------9分
同课章节目录
