2020-2021学年人教版八年级下册第十八章四边形章末小结课件(39张ppt)
文档属性
| 名称 | 2020-2021学年人教版八年级下册第十八章四边形章末小结课件(39张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 23:02:37 | ||
图片预览




文档简介
(共39张PPT)
第十八章
四边形
章末小结
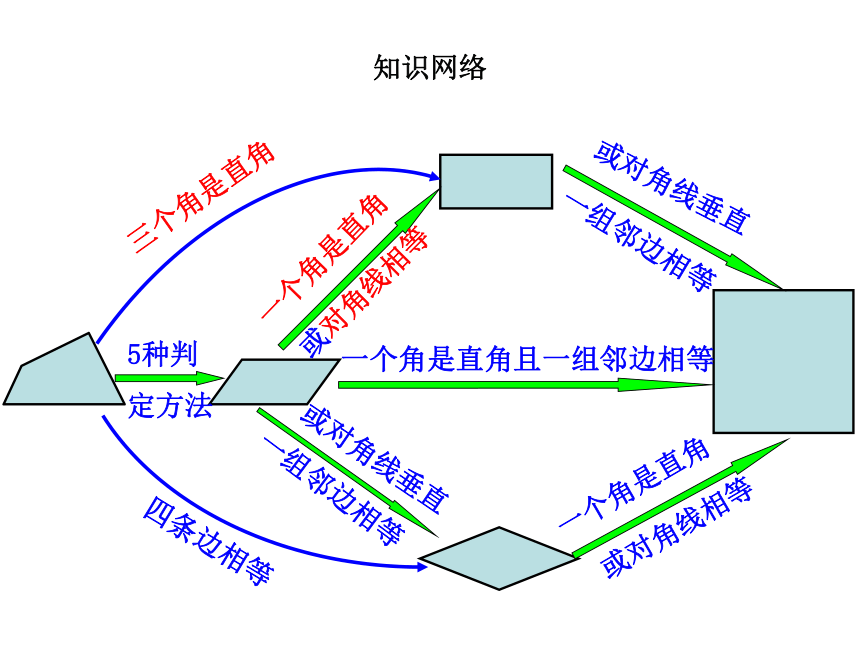
知识网络
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
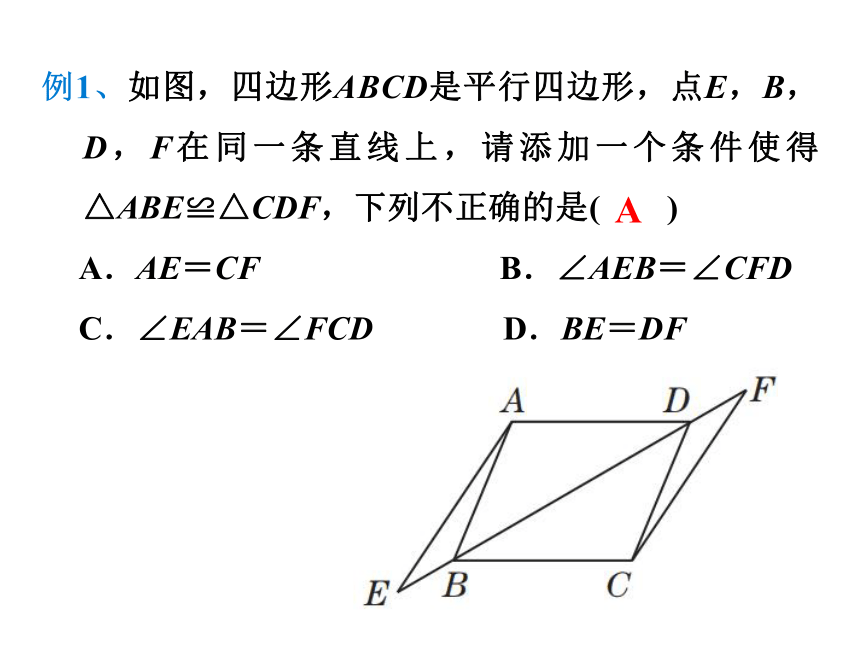
例1、如图,四边形ABCD是平行四边形,点E,B,D,F在同一条直线上,请添加一个条件使得△ABE≌△CDF,下列不正确的是( )
A.AE=CF
B.∠AEB=∠CFD
C.∠EAB=∠FCD
D.BE=DF
A
C
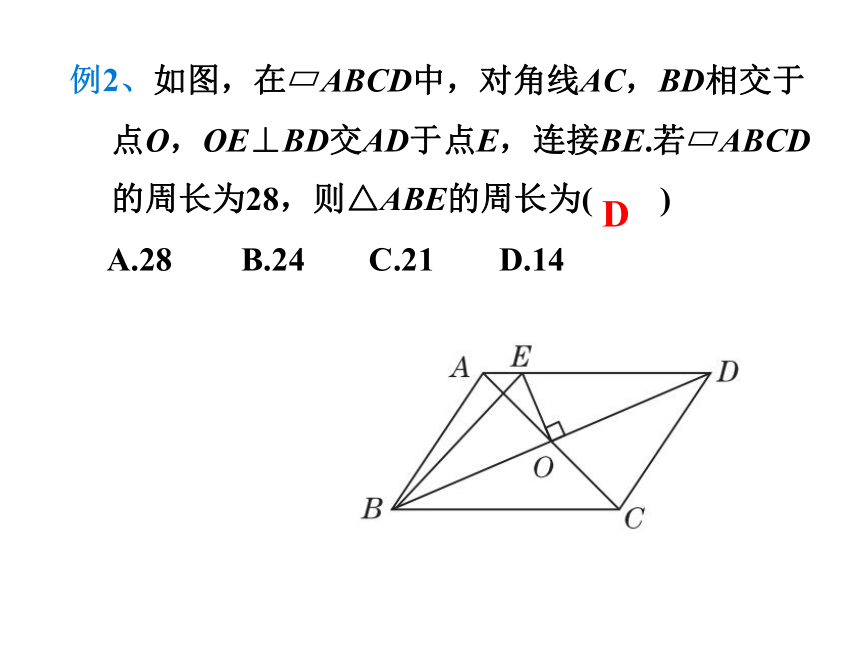
例2、如图,在?ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若?ABCD的周长为28,则△ABE的周长为( )
A.28
B.24
C.21
D.14
D
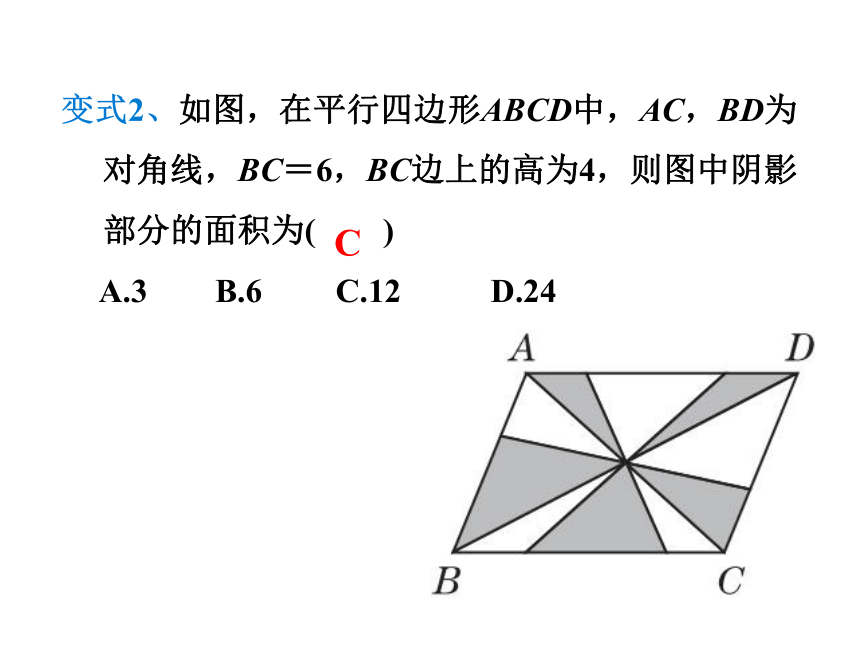
变式2、如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3
B.6
C.12
D.24
C
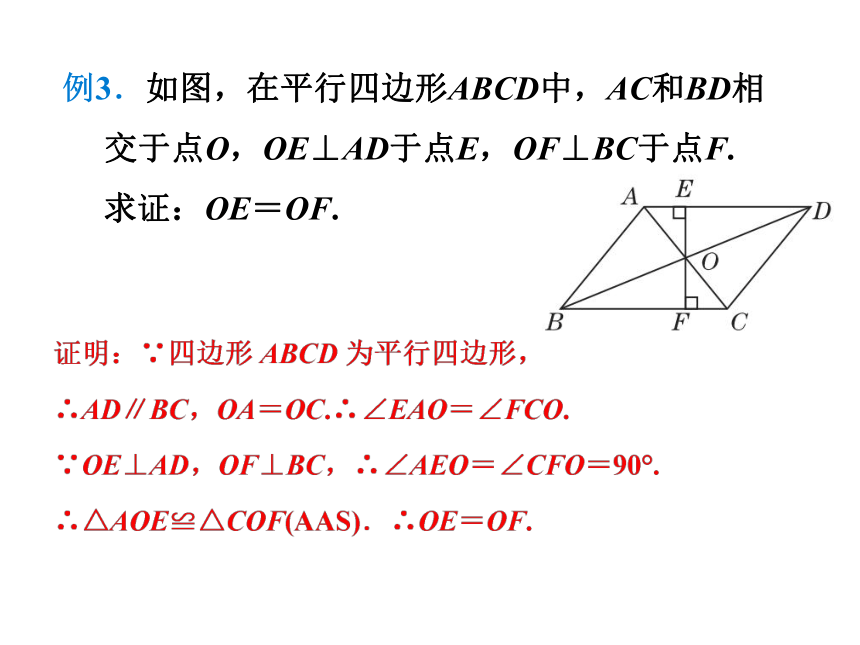
例3.如图,在平行四边形ABCD中,AC和BD相交于点O,OE⊥AD于点E,OF⊥BC于点F.
求证:OE=OF.
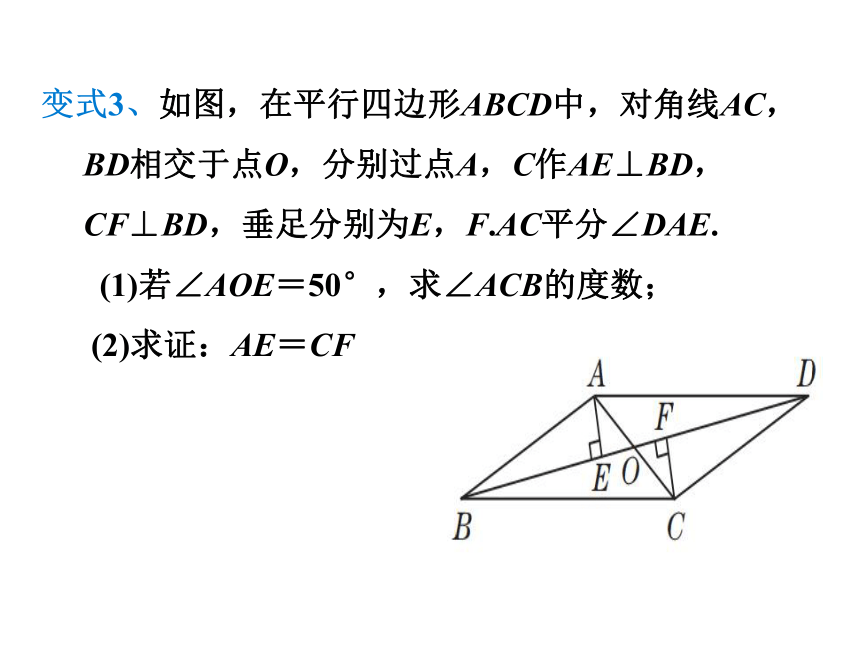
变式3、如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F.AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数;
(2)求证:AE=CF
(2)证明:∵四边形ABCD是,∴OA=OC.
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°.
又∵∠AOE=∠COF,
∴△AEO≌△CFO(AAS).∴AE=CF.
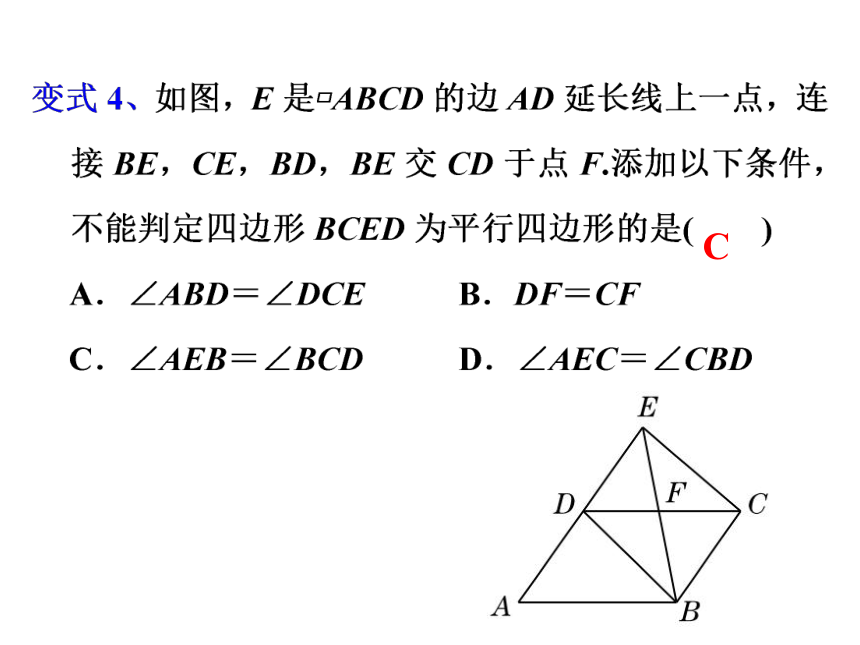
例4、顺次连接平面上A,B,C,D四点得到一个四边形,从①AB∥CD;②BC=AD;③∠A=∠C;④∠B=∠D这4个条件中任取2个,可以得出“四边形ABCD是平行四边形”这一结论的情况共有( )
A.5种
B.4种
C.3种
D.1种
C
C
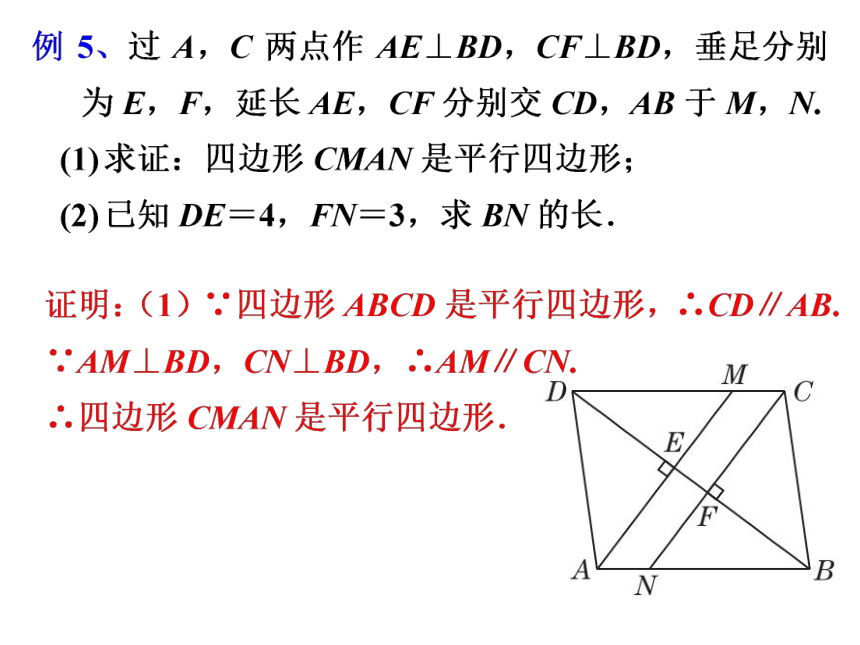
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD.
∵AE=CF,
∴四边形AECF是平行四边形.
(2)解:由(1)得四边形AECF是平行四边形,∴AF∥CE.
∵四边形ABCD是平行四边形,∴AB=CD.
∵AE=CF,∴BE=DF.∵BE∥DF,
∴四边形BFDE是平行四边形.∴BF∥DE.
∴四边形EGFH是平行四边形.
∴EF与GH互相平分.
例6、如图,?ABCD的对角线AC,BD相交于点O,OE∥AB交AD于点E,若OA=1,△AOE的周长等于5,则?ABCD的周长等于________.
16
变式6、如图,M,N分别是△ABC的边AB,AC的中点,若∠A=65°,∠ANM=45°,则∠B=( )
A.20°
B.45°
C.65°
D.70°
D
例7、如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6
cm,BC=8
cm,则EF的长是( )
A.2.2
cm
B.2.3
cm
C.2.4
cm
D.2.5
cm
D
C
例8、如图,在?ABCD中,AE⊥BC,CF⊥AD,E,F分别为垂足.
(1)求证△ABE≌△CDF;
(2)求证:四边形AECF是矩形
(2)∵AD∥BC,
∴∠EAF=∠AEB=90°.
∴∠EAF=∠AEC=∠AFC=90°.
∴四边形AECF是矩形.
变式8、如图,在△ABC中,AB=AC,点D,E分别是线段BC,AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证△BDE≌△FAE;
(2)求证:四边形ADCF为矩形.
证明:(1)∵AF∥BC,
∴∠AFE=∠DBE.
∵E是线段AD的中点,
∴AE=DE.
又∵∠AEF=∠DEB,
∴△BDE≌△FAE;
(2)∵△BDE≌△FAE,
∴AF=BD.
∵D是线段BC的中点,
∴BD=CD.∴AF=CD.
又∵AF∥CD,
∴四边形ADCF是平行四边形.
∵AB=AC,D是BC的中点,
∴AD⊥BC.
∴∠ADC=90°.
∴四边形ADCF为矩形.
例9.如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点.若菱形ABCD的周长为32,则OE的长为( )
A.3
B.4
C.5
D.6
B
变式9、如图,AD是△ABC的中线,四边形ADCE是平行四边形,增加下列条件,能判断?ADCE是菱形的是( )
A.∠BAC=90°
B.∠DAE=90°
C.AB=AC
D.AB=AE
A
例10、如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于点M,N,O为垂足.
(1)求证:四边形BNDM是菱形;
(2)若BD=24,MN=10,
求菱形BNDM的周长.
(2):四边形AECF是菱形,
理由:∵△AOE≌△COF,
∴AE=CF.
又∵AE∥CF,
∴四边形AECF是平行四边形.
又∵EF⊥AC,
∴四边形AECF是菱形.
例11、如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BAE=56°,则∠CEF=________.
22°
例12、如图,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE=DF,连接AE和BF相交于点M.求证AE=BF.
D
例13.如图,已知在Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°后至△DBE,再把△ABC沿射线AB平移至△FEG,DE,FG相交于点H.
(1)判断线段DE,FG的位置关系,并说明理由;
(2)连接CG,求证:四边形CBEG是正方形.
(1)解:DE⊥FG.理由如下:由题意得
∠A=∠EDB=∠GFE,∠ABC=∠DBE=90°,
∴∠EDB+∠BED=90°.
∴∠GFE+∠BED=90°,
∴∠FHE=90°,即DE⊥FG.
(2)证明:∵△ABC沿射线AB平移至△FEG,∴CB∥GE,CB=GE.
∴四边形CBEG是平行四边形.
∵∠ABC=∠GEF=90°,∴四边形CBEG是矩形.
∵BC=BE,∴四边形CBEG是正方形.
变式13.如图,正方形ABCD中,动点E在AC上,AF⊥AC,且AF=AE,连接BF,BE,DE.
(1)求证BF=DE.
(2)当点E运动到AC的中点时(其他条件都保持不变),四边形AFBE是正方形吗?请说明理由.
感谢聆听
第十八章
四边形
章末小结
知识网络
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
例1、如图,四边形ABCD是平行四边形,点E,B,D,F在同一条直线上,请添加一个条件使得△ABE≌△CDF,下列不正确的是( )
A.AE=CF
B.∠AEB=∠CFD
C.∠EAB=∠FCD
D.BE=DF
A
C
例2、如图,在?ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若?ABCD的周长为28,则△ABE的周长为( )
A.28
B.24
C.21
D.14
D
变式2、如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3
B.6
C.12
D.24
C
例3.如图,在平行四边形ABCD中,AC和BD相交于点O,OE⊥AD于点E,OF⊥BC于点F.
求证:OE=OF.
变式3、如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F.AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数;
(2)求证:AE=CF
(2)证明:∵四边形ABCD是,∴OA=OC.
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°.
又∵∠AOE=∠COF,
∴△AEO≌△CFO(AAS).∴AE=CF.
例4、顺次连接平面上A,B,C,D四点得到一个四边形,从①AB∥CD;②BC=AD;③∠A=∠C;④∠B=∠D这4个条件中任取2个,可以得出“四边形ABCD是平行四边形”这一结论的情况共有( )
A.5种
B.4种
C.3种
D.1种
C
C
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD.
∵AE=CF,
∴四边形AECF是平行四边形.
(2)解:由(1)得四边形AECF是平行四边形,∴AF∥CE.
∵四边形ABCD是平行四边形,∴AB=CD.
∵AE=CF,∴BE=DF.∵BE∥DF,
∴四边形BFDE是平行四边形.∴BF∥DE.
∴四边形EGFH是平行四边形.
∴EF与GH互相平分.
例6、如图,?ABCD的对角线AC,BD相交于点O,OE∥AB交AD于点E,若OA=1,△AOE的周长等于5,则?ABCD的周长等于________.
16
变式6、如图,M,N分别是△ABC的边AB,AC的中点,若∠A=65°,∠ANM=45°,则∠B=( )
A.20°
B.45°
C.65°
D.70°
D
例7、如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,连接EF,若AB=6
cm,BC=8
cm,则EF的长是( )
A.2.2
cm
B.2.3
cm
C.2.4
cm
D.2.5
cm
D
C
例8、如图,在?ABCD中,AE⊥BC,CF⊥AD,E,F分别为垂足.
(1)求证△ABE≌△CDF;
(2)求证:四边形AECF是矩形
(2)∵AD∥BC,
∴∠EAF=∠AEB=90°.
∴∠EAF=∠AEC=∠AFC=90°.
∴四边形AECF是矩形.
变式8、如图,在△ABC中,AB=AC,点D,E分别是线段BC,AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证△BDE≌△FAE;
(2)求证:四边形ADCF为矩形.
证明:(1)∵AF∥BC,
∴∠AFE=∠DBE.
∵E是线段AD的中点,
∴AE=DE.
又∵∠AEF=∠DEB,
∴△BDE≌△FAE;
(2)∵△BDE≌△FAE,
∴AF=BD.
∵D是线段BC的中点,
∴BD=CD.∴AF=CD.
又∵AF∥CD,
∴四边形ADCF是平行四边形.
∵AB=AC,D是BC的中点,
∴AD⊥BC.
∴∠ADC=90°.
∴四边形ADCF为矩形.
例9.如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点.若菱形ABCD的周长为32,则OE的长为( )
A.3
B.4
C.5
D.6
B
变式9、如图,AD是△ABC的中线,四边形ADCE是平行四边形,增加下列条件,能判断?ADCE是菱形的是( )
A.∠BAC=90°
B.∠DAE=90°
C.AB=AC
D.AB=AE
A
例10、如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于点M,N,O为垂足.
(1)求证:四边形BNDM是菱形;
(2)若BD=24,MN=10,
求菱形BNDM的周长.
(2):四边形AECF是菱形,
理由:∵△AOE≌△COF,
∴AE=CF.
又∵AE∥CF,
∴四边形AECF是平行四边形.
又∵EF⊥AC,
∴四边形AECF是菱形.
例11、如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BAE=56°,则∠CEF=________.
22°
例12、如图,在正方形ABCD中,点E在BC边的延长线上,点F在CD边的延长线上,且CE=DF,连接AE和BF相交于点M.求证AE=BF.
D
例13.如图,已知在Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°后至△DBE,再把△ABC沿射线AB平移至△FEG,DE,FG相交于点H.
(1)判断线段DE,FG的位置关系,并说明理由;
(2)连接CG,求证:四边形CBEG是正方形.
(1)解:DE⊥FG.理由如下:由题意得
∠A=∠EDB=∠GFE,∠ABC=∠DBE=90°,
∴∠EDB+∠BED=90°.
∴∠GFE+∠BED=90°,
∴∠FHE=90°,即DE⊥FG.
(2)证明:∵△ABC沿射线AB平移至△FEG,∴CB∥GE,CB=GE.
∴四边形CBEG是平行四边形.
∵∠ABC=∠GEF=90°,∴四边形CBEG是矩形.
∵BC=BE,∴四边形CBEG是正方形.
变式13.如图,正方形ABCD中,动点E在AC上,AF⊥AC,且AF=AE,连接BF,BE,DE.
(1)求证BF=DE.
(2)当点E运动到AC的中点时(其他条件都保持不变),四边形AFBE是正方形吗?请说明理由.
感谢聆听
