1.3 勾股定理的应用分层训练- 2021——2022学年 北师大版八年级数学上册(Word版含答案)
文档属性
| 名称 | 1.3 勾股定理的应用分层训练- 2021——2022学年 北师大版八年级数学上册(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 175.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 16:04:03 | ||
图片预览


文档简介
3 勾股定理的应用
【基础练习】
知识点
1 应用勾股定理解决实际问题
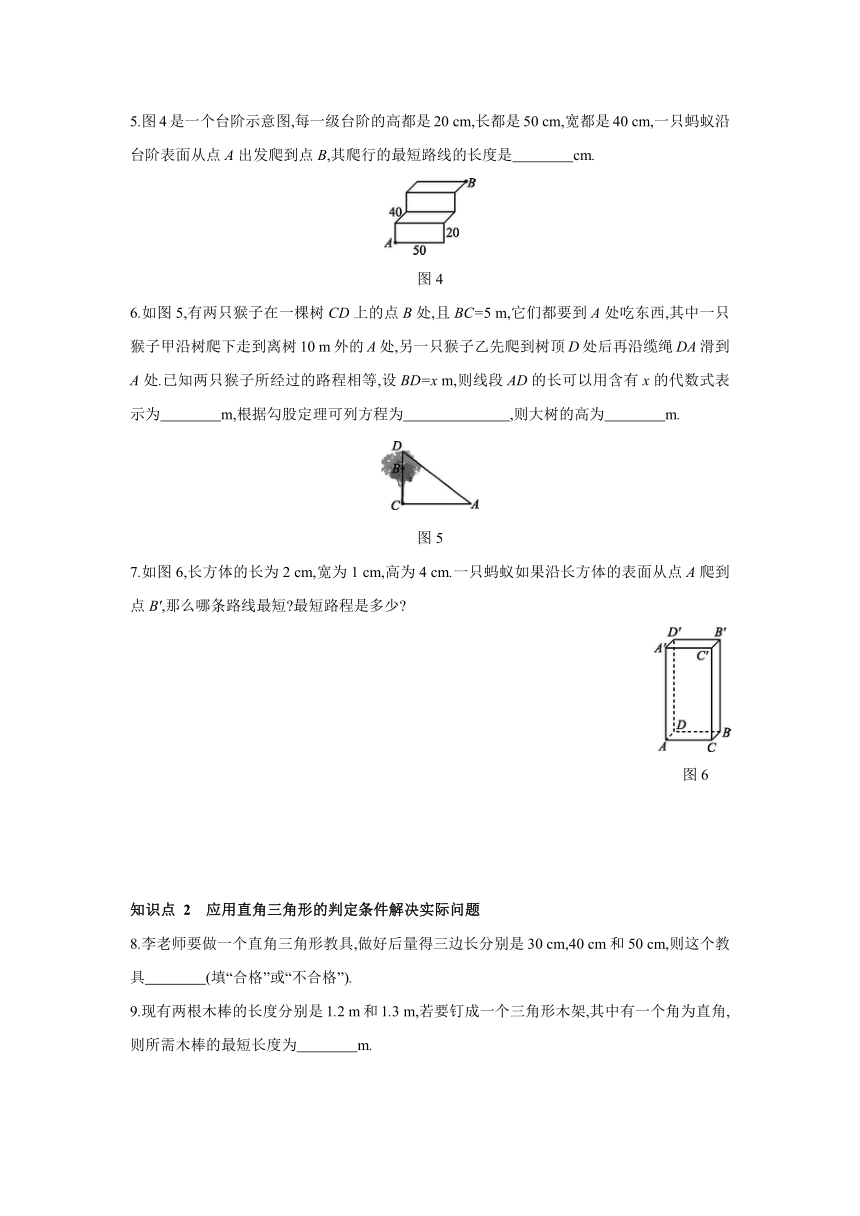
1.如图1所示(示意图),如果梯子AB的底端B到某高楼竖直墙面底端的距离BC为5米,那么13米长的梯子AB的顶端A距地面的高度是( )
图1
A.12米
B.13米
C.14米
D.15米
2.如图2,一圆柱高8
dm,底面半径为2
dm,一只壁虎从上底面的点A爬到下底面上与点A相对的点B处吃食,它爬行的最短路程(π取3)大约是( )
图2
A.20
dm
B.14
dm
C.10
dm
D.无法确定
3.如图3,在一个高为5
m,长为13
m的楼梯表面铺地毯,则地毯的长度至少是 m.?
图3
4.[教材随堂练习变式]
两艘海警船在某小岛附近进行巡航,其中一艘以12海里/时的速度离开该岛向西北方向航行,另一艘同时以16海里/时的速度离开该岛向东北方向航行,经过1.5小时它们相距 海里.?
5.图4是一个台阶示意图,每一级台阶的高都是20
cm,长都是50
cm,宽都是40
cm,一只蚂蚁沿台阶表面从点A出发爬到点B,其爬行的最短路线的长度是 cm.?
图4
6.如图5,有两只猴子在一棵树CD上的点B处,且BC=5
m,它们都要到A处吃东西,其中一只猴子甲沿树爬下走到离树10
m外的A处,另一只猴子乙先爬到树顶D处后再沿缆绳DA滑到A处.已知两只猴子所经过的路程相等,设BD=x
m,则线段AD的长可以用含有x的代数式表示为 m,根据勾股定理可列方程为 ,则大树的高为 m.?
图5
7.如图6,长方体的长为2
cm,宽为1
cm,高为4
cm.一只蚂蚁如果沿长方体的表面从点A爬到点B',那么哪条路线最短?最短路程是多少?
图6
知识点
2 应用直角三角形的判定条件解决实际问题
8.李老师要做一个直角三角形教具,做好后量得三边长分别是30
cm,40
cm和50
cm,则这个教具 (填“合格”或“不合格”).?
9.现有两根木棒的长度分别是1.2
m和1.3
m,若要钉成一个三角形木架,其中有一个角为直角,则所需木棒的最短长度为 m.?
【能力提升】
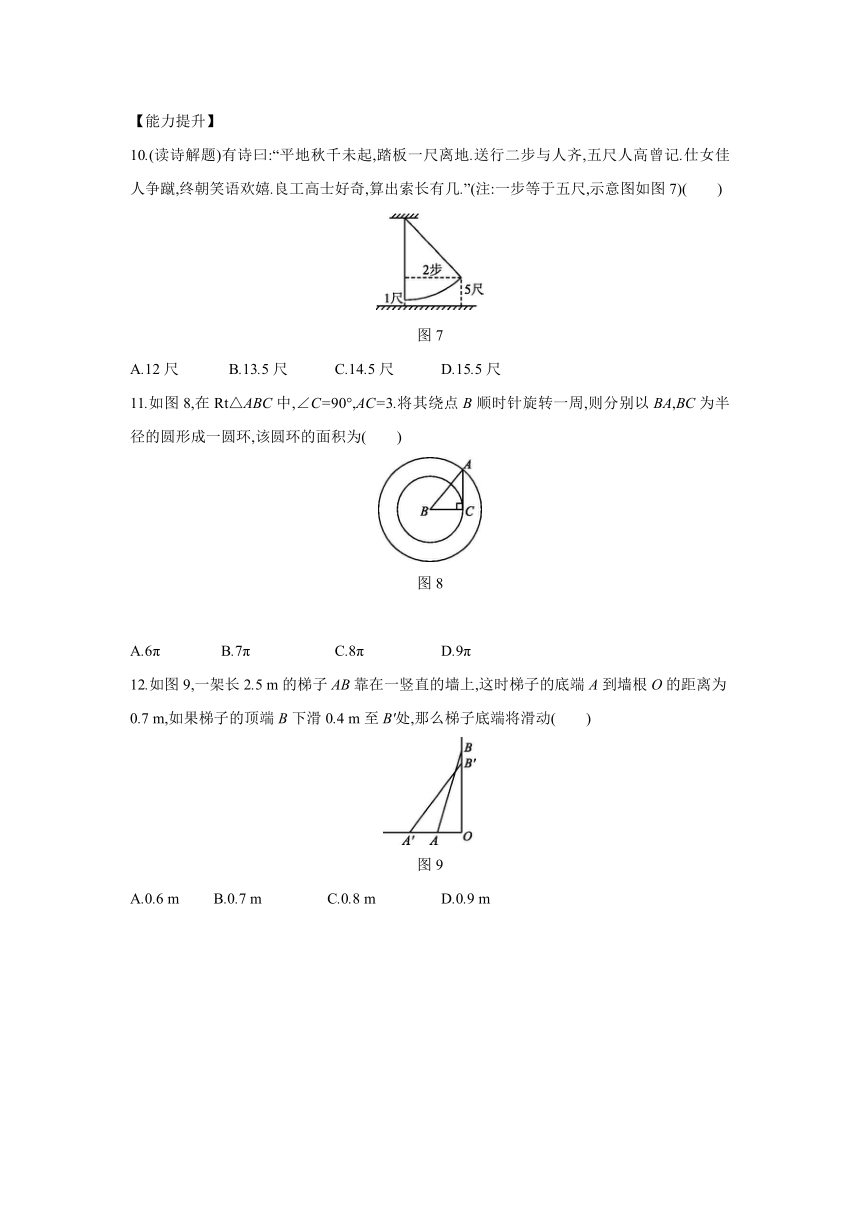
10.(读诗解题)有诗曰:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士好奇,算出索长有几.”(注:一步等于五尺,示意图如图7)( )
图7
A.12尺
B.13.5尺
C.14.5尺
D.15.5尺
11.如图8,在Rt△ABC中,∠C=90°,AC=3.将其绕点B顺时针旋转一周,则分别以BA,BC为半径的圆形成一圆环,该圆环的面积为( )
图8
A.6π
B.7π
C.8π
D.9π
12.如图9,一架长2.5
m的梯子AB靠在一竖直的墙上,这时梯子的底端A到墙根O的距离为0.7
m,如果梯子的顶端B下滑0.4
m至B'处,那么梯子底端将滑动( )
图9
A.0.6
m
B.0.7
m
C.0.8
m
D.0.9
m
13.如图10,一个棱长为3
cm的正方体上有一些线段,把所有的面都分成3×3个小正方形,其边长都为1
cm.假设一只蚂蚁每秒爬行2
cm,则它从下底面点A沿表面爬行至右侧面上的点B,最少要花 s.?
图10
14.如图11,高速公路上有相距10
km的A,B两点,C,D为两村庄,已知DA=4
km,CB=6
km,DA⊥AB于点A,CB⊥AB于点B,现要在AB上建一个服务站E,使得C,D两村庄到服务站E的距离相等,则EA的长是 km.?
图11
15.如图12,∠AOB=90°,OA=45
cm,OB=15
cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
图12
16.为筹备迎春晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠上彩带,如图13所示,已知圆筒高为108
cm,其横截面周长为36
cm,如果在表面缠上4圈彩带,最少应裁剪多长的彩带(彩带宽度忽略不计)?
图13
17.如图14所示,A,B两块试验田相距200
m,C为水源地,AC=160
m,BC=120
m,为了方便灌溉,现有以下两种方案修筑水渠.
甲方案:从水源地C直接修筑两条水渠分别到试验田A,B;
乙方案:过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到线段AB上的点H处,再从H分别向试验田A,B修筑水渠.
(1)请判断△ABC的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
图14
答案
1.A
2.C [解析]
圆柱的高为8
dm,底面半径为2
dm,则其侧面展开图是一个宽为8
dm,长约为12
dm的长方形,如图,连接AB,则AB的长为壁虎爬行的最短路线.由勾股定理,得AB2≈62+82=100,则AB≈10(dm).
3.17 [解析]
由勾股定理,得楼梯的水平宽度的平方=132-52=122,所以楼梯的水平宽度=12
m.所以地毯铺满楼梯,其长度至少应该是楼梯的水平宽度与垂直高度的和,所以地毯的长度至少是12+5=17(m).
4.30 [解析]
依题意画图如下,AC=12×1.5=18(海里),AB=16×1.5=24(海里).
由勾股定理,得BC2=AC2+AB2=182+242=324+576=900.
所以BC=30海里,即经过1.5小时它们相距30海里.
5.130 [解析]
如图,把这个台阶示意图展开为平面图形,连接AB,则AB的长为蚂蚁爬行的最短路线的长.在Rt△ACB中,因为AC=50,BC=120,所以AB2=AC2+BC2=502+1202=16900,所以AB=130,所以蚂蚁沿台阶表面从点A出发爬到点B,其爬行的最短路线的长度为130
cm.
6.(15-x) (x+5)2+102=(15-x)2 7.5
7.解:(1)若蚂蚁沿前面和右面爬行,如图①,则AB'2=AB2+BB'2=(2+1)2+42=25;
(2)若蚂蚁沿前面和上面爬行,如图②,则AB'2=AC2+B'C2=22+(4+1)2=4+25=29;
(3)若蚂蚁沿左面和上面爬行,如图③,则AB'2=AD2+B'D2=12+(4+2)2=1+36=37.
因为25<29<37,所以最短路线应为图①所示,最短路程为5
cm.
8.合格
9.0.5
10.C [解析]
如图,设绳索长为x尺,
则由题意得(x-4)2+102=x2,
解得x=14.5.故选C.
11.D
12.C [解析]
因为AB=2.5
m,AO=0.7
m,
所以BO2=AB2-AO2=2.52-0.72=2.42,所以BO=2.4
m.
因为B'O=BO-BB'=2.4-0.4=2(m),
所以A'O2=2.52-22=1.52,
所以A'O=1.5
m,
所以A'A=A'O-AO=1.5-0.7=0.8(m).
故梯子底端将滑动0.8
m.
故选C.
13.2.5
14.6 [解析]
设BE=x,则AE=(10-x)km.
在Rt△ADE中,
DE2=AD2+AE2=42+(10-x)2.
在Rt△BCE中,
CE2=BC2+BE2=62+x2.
由题意可知DE=CE,则DE2=CE2,
所以42+(10-x)2=62+x2,
解得x=4,
所以EA=10-4=6(km).
15.解:因为小球滚动的速度与机器人行走的速度相等,运动时间相等,所以BC=CA.
设AC为x
cm,则BC=x
cm,OC=(45-x)cm.
由勾股定理可知OB2+OC2=BC2,
所以152+(45-x)2=x2,
解得x=25,
所以BC=25
cm.
答:如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是25
cm.
16.解:如图,将圆筒展开后成为一个长方形,忽略彩带的宽度,整个彩带也随之分成相等的4段,只需求出AC的长度即可.
在Rt△ABC中,
因为AB=36
cm,BC==27(cm),
所以AC2=AB2+BC2=362+272=2025,
所以AC=45
cm,
所以4AC=45×4=180(cm).
答:最少应裁剪180
cm长的彩带.
17.解:(1)因为AC2+BC2=1602+1202=40000,
AB2=2002=40000,
所以AC2+BC2=AB2.
所以△ABC是直角三角形.
(2)甲方案所修的水渠较短.
因为△ABC是直角三角形,
所以△ABC的面积=AB·CH=AC·BC.
所以CH===96(m).
因为AC+BC=160+120=280(m),CH+AH+BH=CH+AB=96+200=296(m),
所以AC+BC所以甲方案所修的水渠较短.
【基础练习】
知识点
1 应用勾股定理解决实际问题
1.如图1所示(示意图),如果梯子AB的底端B到某高楼竖直墙面底端的距离BC为5米,那么13米长的梯子AB的顶端A距地面的高度是( )
图1
A.12米
B.13米
C.14米
D.15米
2.如图2,一圆柱高8
dm,底面半径为2
dm,一只壁虎从上底面的点A爬到下底面上与点A相对的点B处吃食,它爬行的最短路程(π取3)大约是( )
图2
A.20
dm
B.14
dm
C.10
dm
D.无法确定
3.如图3,在一个高为5
m,长为13
m的楼梯表面铺地毯,则地毯的长度至少是 m.?
图3
4.[教材随堂练习变式]
两艘海警船在某小岛附近进行巡航,其中一艘以12海里/时的速度离开该岛向西北方向航行,另一艘同时以16海里/时的速度离开该岛向东北方向航行,经过1.5小时它们相距 海里.?
5.图4是一个台阶示意图,每一级台阶的高都是20
cm,长都是50
cm,宽都是40
cm,一只蚂蚁沿台阶表面从点A出发爬到点B,其爬行的最短路线的长度是 cm.?
图4
6.如图5,有两只猴子在一棵树CD上的点B处,且BC=5
m,它们都要到A处吃东西,其中一只猴子甲沿树爬下走到离树10
m外的A处,另一只猴子乙先爬到树顶D处后再沿缆绳DA滑到A处.已知两只猴子所经过的路程相等,设BD=x
m,则线段AD的长可以用含有x的代数式表示为 m,根据勾股定理可列方程为 ,则大树的高为 m.?
图5
7.如图6,长方体的长为2
cm,宽为1
cm,高为4
cm.一只蚂蚁如果沿长方体的表面从点A爬到点B',那么哪条路线最短?最短路程是多少?
图6
知识点
2 应用直角三角形的判定条件解决实际问题
8.李老师要做一个直角三角形教具,做好后量得三边长分别是30
cm,40
cm和50
cm,则这个教具 (填“合格”或“不合格”).?
9.现有两根木棒的长度分别是1.2
m和1.3
m,若要钉成一个三角形木架,其中有一个角为直角,则所需木棒的最短长度为 m.?
【能力提升】
10.(读诗解题)有诗曰:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士好奇,算出索长有几.”(注:一步等于五尺,示意图如图7)( )
图7
A.12尺
B.13.5尺
C.14.5尺
D.15.5尺
11.如图8,在Rt△ABC中,∠C=90°,AC=3.将其绕点B顺时针旋转一周,则分别以BA,BC为半径的圆形成一圆环,该圆环的面积为( )
图8
A.6π
B.7π
C.8π
D.9π
12.如图9,一架长2.5
m的梯子AB靠在一竖直的墙上,这时梯子的底端A到墙根O的距离为0.7
m,如果梯子的顶端B下滑0.4
m至B'处,那么梯子底端将滑动( )
图9
A.0.6
m
B.0.7
m
C.0.8
m
D.0.9
m
13.如图10,一个棱长为3
cm的正方体上有一些线段,把所有的面都分成3×3个小正方形,其边长都为1
cm.假设一只蚂蚁每秒爬行2
cm,则它从下底面点A沿表面爬行至右侧面上的点B,最少要花 s.?
图10
14.如图11,高速公路上有相距10
km的A,B两点,C,D为两村庄,已知DA=4
km,CB=6
km,DA⊥AB于点A,CB⊥AB于点B,现要在AB上建一个服务站E,使得C,D两村庄到服务站E的距离相等,则EA的长是 km.?
图11
15.如图12,∠AOB=90°,OA=45
cm,OB=15
cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
图12
16.为筹备迎春晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠上彩带,如图13所示,已知圆筒高为108
cm,其横截面周长为36
cm,如果在表面缠上4圈彩带,最少应裁剪多长的彩带(彩带宽度忽略不计)?
图13
17.如图14所示,A,B两块试验田相距200
m,C为水源地,AC=160
m,BC=120
m,为了方便灌溉,现有以下两种方案修筑水渠.
甲方案:从水源地C直接修筑两条水渠分别到试验田A,B;
乙方案:过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到线段AB上的点H处,再从H分别向试验田A,B修筑水渠.
(1)请判断△ABC的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
图14
答案
1.A
2.C [解析]
圆柱的高为8
dm,底面半径为2
dm,则其侧面展开图是一个宽为8
dm,长约为12
dm的长方形,如图,连接AB,则AB的长为壁虎爬行的最短路线.由勾股定理,得AB2≈62+82=100,则AB≈10(dm).
3.17 [解析]
由勾股定理,得楼梯的水平宽度的平方=132-52=122,所以楼梯的水平宽度=12
m.所以地毯铺满楼梯,其长度至少应该是楼梯的水平宽度与垂直高度的和,所以地毯的长度至少是12+5=17(m).
4.30 [解析]
依题意画图如下,AC=12×1.5=18(海里),AB=16×1.5=24(海里).
由勾股定理,得BC2=AC2+AB2=182+242=324+576=900.
所以BC=30海里,即经过1.5小时它们相距30海里.
5.130 [解析]
如图,把这个台阶示意图展开为平面图形,连接AB,则AB的长为蚂蚁爬行的最短路线的长.在Rt△ACB中,因为AC=50,BC=120,所以AB2=AC2+BC2=502+1202=16900,所以AB=130,所以蚂蚁沿台阶表面从点A出发爬到点B,其爬行的最短路线的长度为130
cm.
6.(15-x) (x+5)2+102=(15-x)2 7.5
7.解:(1)若蚂蚁沿前面和右面爬行,如图①,则AB'2=AB2+BB'2=(2+1)2+42=25;
(2)若蚂蚁沿前面和上面爬行,如图②,则AB'2=AC2+B'C2=22+(4+1)2=4+25=29;
(3)若蚂蚁沿左面和上面爬行,如图③,则AB'2=AD2+B'D2=12+(4+2)2=1+36=37.
因为25<29<37,所以最短路线应为图①所示,最短路程为5
cm.
8.合格
9.0.5
10.C [解析]
如图,设绳索长为x尺,
则由题意得(x-4)2+102=x2,
解得x=14.5.故选C.
11.D
12.C [解析]
因为AB=2.5
m,AO=0.7
m,
所以BO2=AB2-AO2=2.52-0.72=2.42,所以BO=2.4
m.
因为B'O=BO-BB'=2.4-0.4=2(m),
所以A'O2=2.52-22=1.52,
所以A'O=1.5
m,
所以A'A=A'O-AO=1.5-0.7=0.8(m).
故梯子底端将滑动0.8
m.
故选C.
13.2.5
14.6 [解析]
设BE=x,则AE=(10-x)km.
在Rt△ADE中,
DE2=AD2+AE2=42+(10-x)2.
在Rt△BCE中,
CE2=BC2+BE2=62+x2.
由题意可知DE=CE,则DE2=CE2,
所以42+(10-x)2=62+x2,
解得x=4,
所以EA=10-4=6(km).
15.解:因为小球滚动的速度与机器人行走的速度相等,运动时间相等,所以BC=CA.
设AC为x
cm,则BC=x
cm,OC=(45-x)cm.
由勾股定理可知OB2+OC2=BC2,
所以152+(45-x)2=x2,
解得x=25,
所以BC=25
cm.
答:如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是25
cm.
16.解:如图,将圆筒展开后成为一个长方形,忽略彩带的宽度,整个彩带也随之分成相等的4段,只需求出AC的长度即可.
在Rt△ABC中,
因为AB=36
cm,BC==27(cm),
所以AC2=AB2+BC2=362+272=2025,
所以AC=45
cm,
所以4AC=45×4=180(cm).
答:最少应裁剪180
cm长的彩带.
17.解:(1)因为AC2+BC2=1602+1202=40000,
AB2=2002=40000,
所以AC2+BC2=AB2.
所以△ABC是直角三角形.
(2)甲方案所修的水渠较短.
因为△ABC是直角三角形,
所以△ABC的面积=AB·CH=AC·BC.
所以CH===96(m).
因为AC+BC=160+120=280(m),CH+AH+BH=CH+AB=96+200=296(m),
所以AC+BC
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
