《7.4 平行线的性质》课时同步训练 2021-2022学年北师大版数学八年级上册(word版含解析)
文档属性
| 名称 | 《7.4 平行线的性质》课时同步训练 2021-2022学年北师大版数学八年级上册(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 334.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 08:05:38 | ||
图片预览


文档简介
1118870010858500《7.4 平行线的性质》课时同步训练2021-2022年数学北师大版八(上)
一.选择题(共6小题)
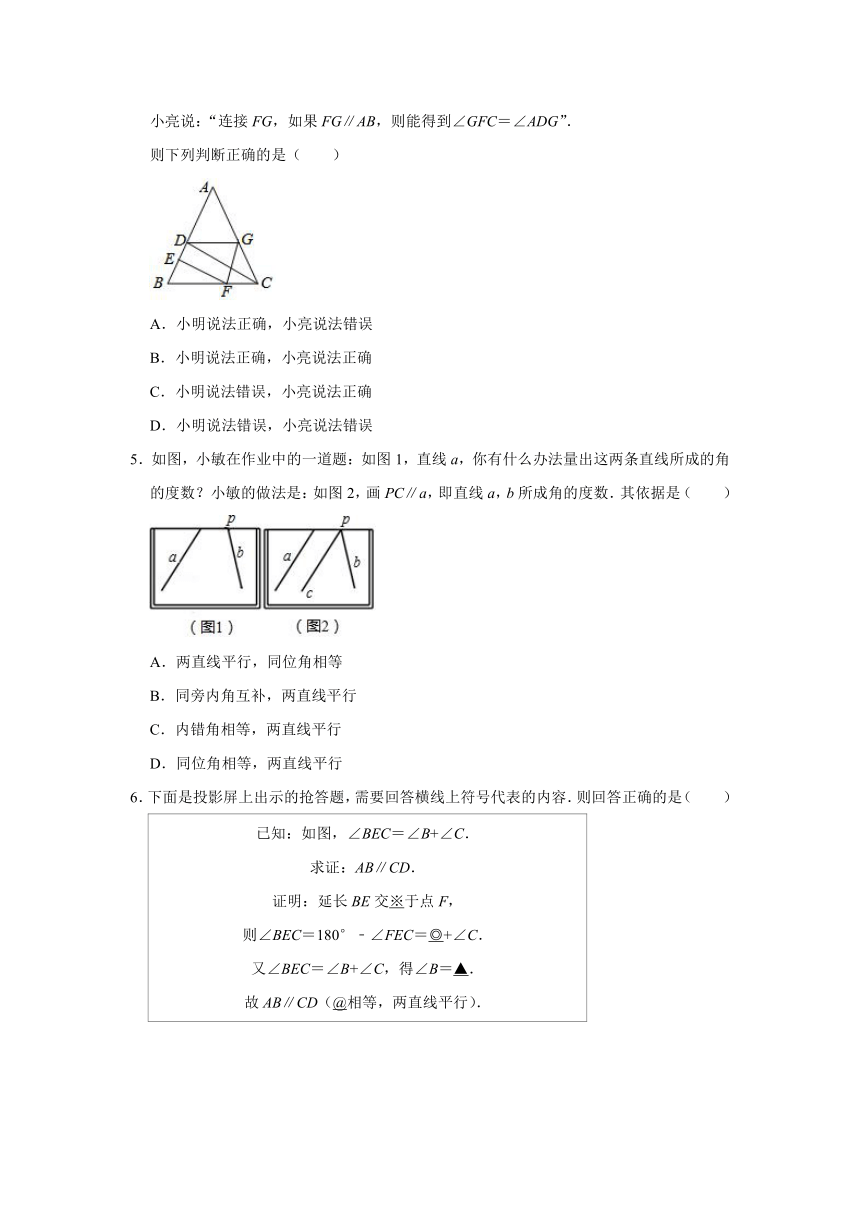
1.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠2=∠3,则b∥c D.若∠1+∠5=180°,则d∥e
2.如图a∥b,c与a相交,d与b相交
①若∠1=∠2,则∠3=∠4;
②若∠1+∠4=180°,则c∥d;
③∠4﹣∠2=∠3﹣∠1;
④∠1+∠2+∠3+∠4=360°,正确的有( )
A.①③④ B.①②③ C.①②④ D.②③
3.如图,已知∠1=∠2=∠3=50°,则∠4的度数为( )
A.50° B.100° C.130° D.150°
4.小明和小亮在研究一道数学题,如图EF⊥AB,CD⊥AB,D,G在AC上.
小明说:“如果∠CDG=∠BFE,则能得到∠AGD=∠ACB”;
小亮说:“连接FG,如果FG∥AB,则能得到∠GFC=∠ADG”.
则下列判断正确的是( )
A.小明说法正确,小亮说法错误
B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确
D.小明说法错误,小亮说法错误
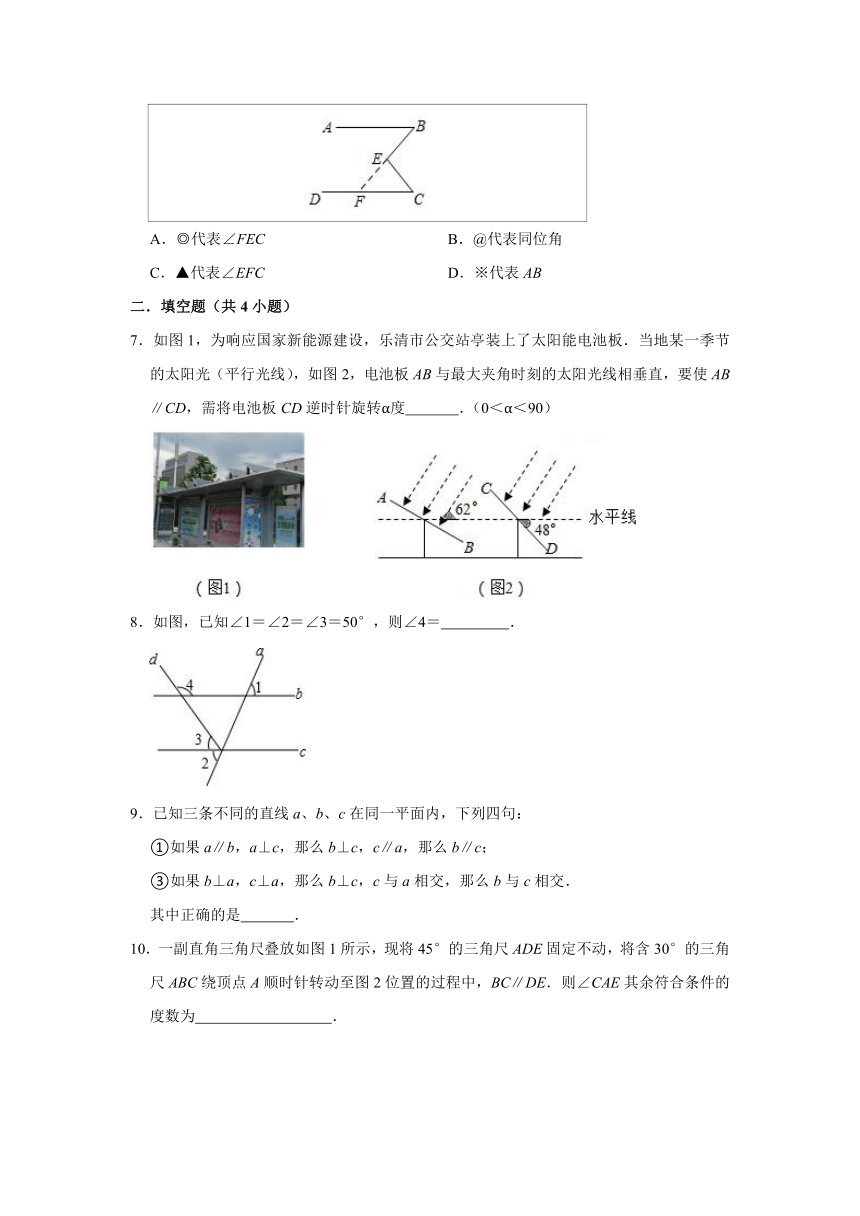
5.如图,小敏在作业中的一道题:如图1,直线a,你有什么办法量出这两条直线所成的角的度数?小敏的做法是:如图2,画PC∥a,即直线a,b所成角的度数.其依据是( )
A.两直线平行,同位角相等
B.同旁内角互补,两直线平行
C.内错角相等,两直线平行
D.同位角相等,两直线平行
6.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容.则回答正确的是( )
已知:如图,∠BEC=∠B+∠C.
求证:AB∥CD.
证明:延长BE交※于点F,
则∠BEC=180°﹣∠FEC=◎+∠C.
又∠BEC=∠B+∠C,得∠B=▲.
故AB∥CD(@相等,两直线平行).
A.◎代表∠FEC B.@代表同位角
C.▲代表∠EFC D.※代表AB
二.填空题(共4小题)
7.如图1,为响应国家新能源建设,乐清市公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线),如图2,电池板AB与最大夹角时刻的太阳光线相垂直,要使AB∥CD,需将电池板CD逆时针旋转α度 .(0<α<90)
8.如图,已知∠1=∠2=∠3=50°,则∠4= .
9.已知三条不同的直线a、b、c在同一平面内,下列四句:
①如果a∥b,a⊥c,那么b⊥c,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c,c与a相交,那么b与c相交.
其中正确的是 .
10.一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动至图2位置的过程中,BC∥DE.则∠CAE其余符合条件的度数为 .
三.解答题(共15小题)
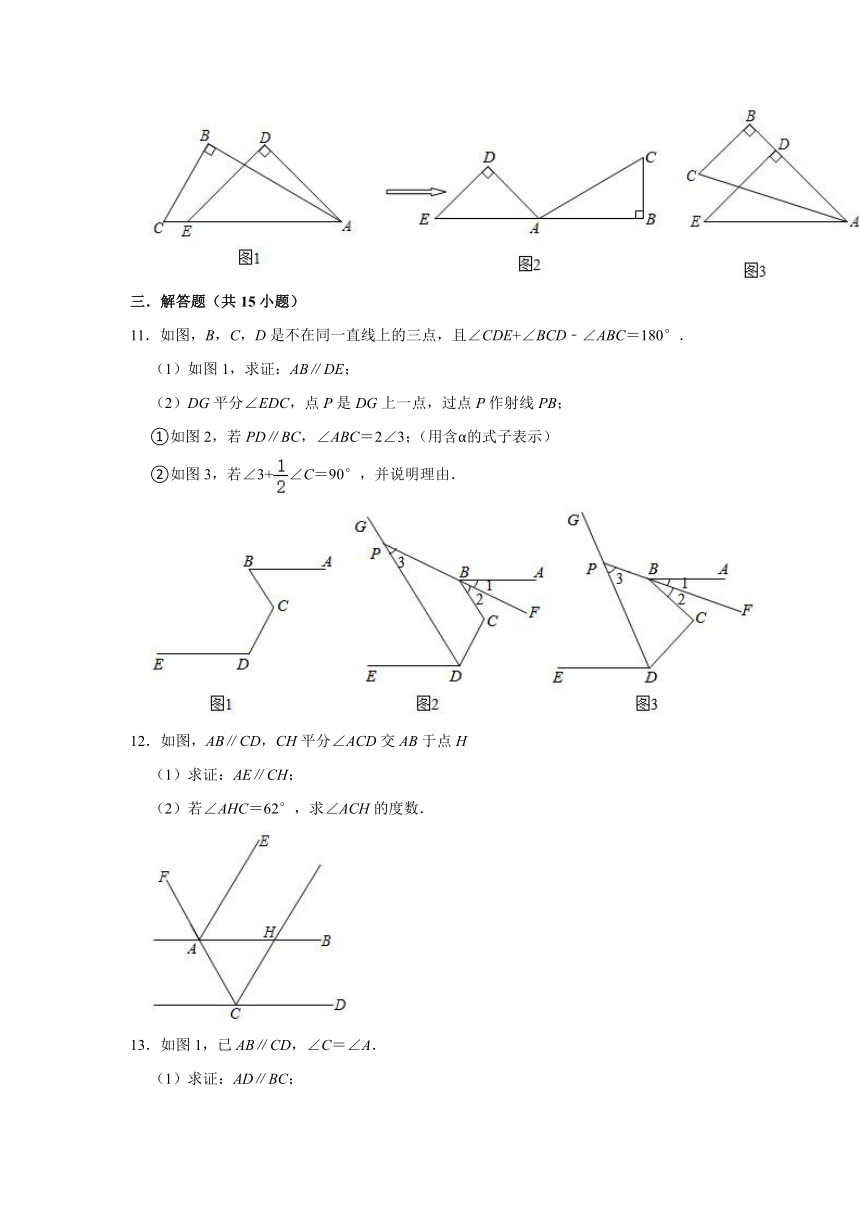
11.如图,B,C,D是不在同一直线上的三点,且∠CDE+∠BCD﹣∠ABC=180°.
(1)如图1,求证:AB∥DE;
(2)DG平分∠EDC,点P是DG上一点,过点P作射线PB;
①如图2,若PD∥BC,∠ABC=2∠3;(用含α的式子表示)
②如图3,若∠3+∠C=90°,并说明理由.
12.如图,AB∥CD,CH平分∠ACD交AB于点H
(1)求证:AE∥CH;
(2)若∠AHC=62°,求∠ACH的度数.
13.如图1,已AB∥CD,∠C=∠A.
(1)求证:AD∥BC;
(2)如图2,若点E是在平行线AB,CD内,探究∠BAE,∠CDE,并证明.
(3)如图3,若∠C=90°,且点E在线段BC上,射线DF在∠EDC的内部,且交BC于点M,∠AED+∠AEC=180°,
①直接写出∠AED与∠FDC的数量关系: .
②点P在射线DA上,且满足∠DEP=2∠F,∠DEA﹣∠PEA=,补全图形后,求∠EPD的度数.
14.如图,已知∠A=∠FEC,∠DEF=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠BDC=3∠B,求∠EFC的度数.
15.如图,AD∥BC,∠1=∠B
(1)求证:AB∥DE;
(2)AF与DC有什么位置关系?为什么?
(3)若∠B=68°,∠C=46°,求∠2的度数.
16.已知:如图,点E在BC上,BD⊥AC,垂足分别为D、F,点M、G在AB上,∠1=∠2.
求证:∠DMB+∠ABC=180°.
小勇在做上面这道题时用了以下推理过程.请帮他在横线上填写结论,在括号内填写推理依据.
证明:∵BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
∴∠BDC=90°,∠EFC=90° ( ).
∴∠BDC=∠EFC(等量代换).
∴ (同位角相等,两直线平行).
∴∠CBD=∠2 .
∵∠1=∠2(已知).
∴∠CBD=∠1 ( ).
∴ ( ).
∵∠AMD=∠AGF(已知).
∴GF∥MD(同位角相等,两直线平行).
∴BC∥MD ( ).
∴∠DMB+∠ABC=180° ( ).
17.已知,如图1,射线PE分别与直线AB,∠PFD的平分线与直线AB相交于点M,射线PM交CD于点N,∠EMF=β°,且(40﹣2α)2+|β﹣20|=0.
(1)α= ,β= ;直线AB与CD的位置关系是 ;
(2)如图2,若点G、H分别在射线MA和线段MF上,且∠MGH=∠PNF,并证明你的结论;
(3)若将图中的射线PM绕着端点P逆时针方向旋转(如图3),分别与AB、CD相交于点M1和点N1时,作∠PM1B的角平分线M1Q与射线FM相交于点Q,问在旋转的过程中的值是否改变?若不变;若变化,请说明理由.
18.如图,在四边形ABCD中,AE,点E在CD上,∠1+∠2=90°
(1)完成下面的说理过程解:
解:∵AE平分∠BAD(已知),
∴∠BAD=2∠1( ),
∵BE平分∠ABC(已知),
∴∠ABC=2∠2( ),
∴∠BAD+∠ABC=2∠1+2∠2( ),
∵∠1+∠2=90°(已知),
∴∠BAD+∠ABC=180°,
∴AD∥BC( ).
(2)若AE平分∠DEF,试说明BE平分∠CEF.
19.如图,E,G是分别是AB,AC上的点,F,连接EF,AD,如果AB∥DG,∠1+∠2=180°.
(1)判断AD与EF的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠2=145°,求∠B的度数.
20.如图,已知∠C=∠B,AB∥CD.
(1)试着先判断CF与BD所在的直线平行?请说明理由.
(2)如果AB是∠FAD的平分线,且∠ADB=106°,求∠B的度数.
21.(1)如图,已知∠1=∠2,∠3=65°
(2)一艘船从O处出发沿北偏东60°方向行驶至A,然后向正东方向行驶至C后又改变航向,朝与出发时相反的方向行驶至B.请画出该船的航线示意图
22.如图,已知点A在EF上,点P,∠E=∠EMA,∠BQM=∠BMQ.
(1)求证:EF∥BC;
(2)若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.
23.阅读下面材料:
小亮同学遇到这样一个问题:
已知:如图甲,AB∥CD,E为AB,连接BE,DE
求证:∠BED=∠B+∠D.
(1)小亮写出了该问题的证明,请你帮他把证明过程补充完整.
证明:过点E作EF∥AB,
则有∠BEF= .
∵AB∥CD,
∴ ∥ ,
∴∠FED= .
∴∠BED=∠BEF+∠FED=∠B+∠D.
(2)请你参考小亮思考问题的方法,解决问题:如图乙,
已知:直线a∥b,点A,B在直线a上,D在直线b上,连接AD,BE平分∠ABC,DE平分∠ADC,DE所在的直线交于点E.
①如图1,当点B在点A的左侧时,若∠ABC=60°,求∠BED的度数;
②如图2,当点B在点A的右侧时,设∠ABC=α,请你求出∠BED的度数(用含有α,β的式子表示).
24.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,连接GN,若∠N=∠AGM∠FGN,求∠MHG的度数.
25.如图,已知∠1=∠CDF,∠2+∠3=180°.
(1)请你判断AD与EC的位置关系,并说明理由;
(2)若CE⊥EF,且∠3=140°,求∠FAB的度数.
参考答案
一.选择题(共6小题)
1.解:A、若a∥b,则a∥c,正确;
B、若∠1=∠2,利用了内错角相等,正确;
C、∠3=∠2,错误;
D、若∠1+∠6=180°,利用同旁内角互补,正确;
故选:C.
2.解:
①若∠1=∠2,则a∥e∥b,故此说法正确;
②若∠4+∠4=180°,由a∥b得到,则∠1=∠8;故此说法正确;
③由a∥b得到,∠5+∠4=180°,∠5+∠3+180°﹣∠4+180°﹣∠2=360°,故此说法正确;
④由③得,只有∠1+∠4=∠7+∠3=180°时.故此说法错误.
故选:B.
3.解:∵∠1=∠BFE=50°,
∴∠BFE=∠2=50°,
∴AB∥CD,
∴∠3=∠NEC,
∵∠NEC=180°﹣∠3=180°﹣50°=130°,
∴∠4=130°,
故选:C.
4.解:∵EF⊥AB,CD⊥AB,
∴CD∥EF,
若∠CDG=∠BFE,
∵∠BCD=∠BFE,
∴∠BCD=∠CDG,
∴DG∥BC,
∴∠AGD=∠ACB,故小明说法正确;
∵FG∥AB,
∴∠B=∠GFC,
故得不到∠GFC=∠ADG,故小亮说法错误,
故选:A.
5.解:根据两直线平行,同位角相等得到直线a和直线b的夹角与直线b和直线PC的夹角相等.
故选:A.
6.证明:延长BE交CD于点F,
则∠BEC=180°﹣∠FEC=∠EFC+∠C.
又∠BEC=∠B+∠C,得∠B=∠EFC.
故AB∥CD(内错角相等,两直线平行).
所以※代表CD,◎代表∠EFC,@代表内错角,
故选:C.
二.填空题(共4小题)
7.解:
∵EF⊥AB,
∴∠EFO=90°,
∵∠OEF=62°,
∴∠EOF=180°﹣90°﹣62°=28°,
∵AB∥CD,
∴∠MQD=∠EOF=28°,
∵要使AB∥CD,需将电池板CD逆时针旋转α度,
∴α°=48°﹣28°=20°,
故答案为:20.
8.解:∵∠1=∠2,∠4=∠5,
∴∠5=∠3,
∴b∥c,
∴∠3+∠6=180°,
∵∠6=50°,
∴∠6=130°,
∴∠4=130°.
故答案为:130°.
9.解:∵直线a,b,c在同一平面内,
∴①如果a∥b,a⊥c;
②如果b∥a,c∥a;
③如果b⊥a,c⊥a,故错误;
④如果b⊥a,c与a相交,故错误.
故正确的是①②.
故答案为:①②.
10.解:如图3,当BC∥DE时;
如图,当AE∥BC时;
如图,当DE∥AB(或AD∥BC)时;
如图,当DE∥AC时.
综上所述,旋转后两块三角板至少有一组边平行,
故答案为:60°或105°或135°.
三.解答题(共15小题)
11.解:(1)如图1,延长DC交AB于点F,
∵∠BFC=∠BCD﹣∠ABC,
∴∠CDE+∠BCD﹣∠ABC=180°,
即∠CDE+∠BFC=180°,
∴AB∥DE;
(2)①∵PD∥BC,
∴∠2=∠4,
又∵∠ABC=2∠3,∠ABC=∠5+∠2,
∴∠1=∠8=∠3=α,∠ABC=2α,
∵DG平分∠EDC,∠CDG+∠C=180°,
∴∠EDC+∠C=180°,①
∵∠CDE+∠BCD﹣∠ABC=180°,
即∠CDE+∠C﹣2α=180°,②
联立①②解得∠C=180°﹣2α;
②∠1=∠2,理由如下:
如图4,作CH平分∠C交DG于H,
∴∠4=∠5=∠BCD,
∵DG平分∠EDC,
∴∠CDG=∠EDC,
∴∠5+∠CDG=(∠BCD+∠EDC),
又∵∠CDE+∠BCD﹣∠ABC=180°,
∴∠5+∠CDG=(180°+∠ABC)=90°+,
∴∠PHC=90°+∠ABC,
∵∠3+∠C=90°,
∴∠3+∠7=90°,
∴∠PBC=360°﹣∠3﹣∠4﹣∠PHC=360°﹣90°﹣90°﹣∠ABC=180°﹣,
又∵∠PBC+∠2=180°,
∴∠2=∠ABC,
∴∠1=∠6.
12.(1)证明:∵AB∥CD,
∴∠FAB=∠FCD,
∵AE平分∠FAB,CH平分∠ACD,
∴∠FAE=∠FAB∠FCD,
∴∠FAE=∠FCH,
∴AE∥CH;
(2)∵AB∥CD,
∴∠AHC=∠HCD,
∵∠AHC=62°,
∴∠HCD=62°,
∵CH平分∠ACD,
∴∠ACH=∠HCD=62°.
13.(1)证明:AB∥CD,
∴∠A+∠D=180°,
∵∠C=∠A,
∴∠C+∠D=180°,
∴AD∥BC;
(2)∠BAE+∠CDE=∠AED,理由如下:
如图2,过点E作EF∥AB,
∵AB∥CD
∴AB∥CD∥EF
∴∠BAE=∠AEF,∠CDE=∠DEF
即∠BAE+∠EAD+∠CDE+∠DEF=180°
∴∠BAE+∠CDE=∠AED;
(3)①∠AED﹣∠FDC=45°;
∵∠AED+∠AEC=180°,∠AED+∠DEC+∠AEB=180°,
∴∠AEC=∠DEC+∠AEB,
∴∠AED=∠AEB,∠DEC=90°﹣2∠FDC,
∴3∠AED+(90°﹣2∠FDC)=180°,
∴∠AED﹣∠FDC=45°,
故答案为:∠AED﹣∠FDC=45°;
②如图3,
∵∠AED=∠F+∠FDE,∠AED﹣∠FDC=45°,
∴∠F=45°,
∴∠DEP=4∠F=90°,
∵∠DEA﹣∠PEA=∠DEB=,
∴∠PEA=∠AED,
∴∠DEP=∠PEA+∠AED=∠AED=90°,
∴∠AED=70°,
∵∠AED+∠AEC=180°,
∴∠DEC+2∠AED=180°,
∴∠DEC=40°,
∵AD∥BC,
∴∠ADE=∠DEC=40°,
在△PDE中,∠EPD=180°﹣∠DEP﹣∠AED=50°,
即∠EPD=50°.
14.解:(1)DE∥BC,理由如下:
∵∠A=∠FEC,
∴AB∥EF,
∴∠DEF=∠ADE,
∵∠DEF=∠B,
∴∠ADE=∠B,
∴DE∥BC;
(2)设∠B=x,则∠BDC=3∠B=3x,
∵DE∥BC,
∴∠ADE=∠B=x,
∵DE平分∠ADC,
∴∠ADC=7∠ADE=2x,
∴∠BDC+∠ADC=180°,
∴3x+8x=180°,
∴x=36°,
∴∠ADC=2x=72°,
∵AB∥EF,
∴∠EFC=∠ADC=72°.
15.(1)证明:∵AD∥BC(已知),
∴∠1=∠DEC(两直线平行,内错角相等),
∵∠1=∠B(已知),
∴∠DEC=∠B(等量代换),
∴AB∥DE(同位角相等,两直线平行);
(2)解:AF∥DC,
理由如下:
∵AB∥DE(已证),
∴∠5=∠AGD(两直线平行,内错角相等),
∵∠2=∠3(已知),
∴∠AGD=∠5(等量代换),
∴AF∥DC(内错角相等,两直线平行);
(3)∵AF∥DC,∠C=46°,
∴∠AFB=∠C=46°(两直线平行,同位角相等),
∵∠B=68°,∠2+∠B+∠AFB=180°,
∴∠2=180°﹣∠B﹣∠AFB=180°﹣46°﹣68°=66°.
16.证明:∵BD⊥AC,EF⊥AC、F(已知),
∴∠BDC=90°,∠EFC=90°( ),
∴∠BDC=∠EFC(等量代换),
∴BD∥EF(同位角相等,两直线平行),
∴∠CBD=∠2( 两直线平行 ),
∵∠1=∠2(已知),
∴∠CBD=∠1(等量代换),
∴GF∥BC(内错角相等,两直线平行 ),
∵∠AMD=∠AGF(已知),
∴GF∥MD(同位角相等,两直线平行),
∴BC∥MD(平行公理的推论),
∴∠DMB+∠ABC=180°(两直线平行,同旁内角互补),
故答案为:垂直的定义,BD∥EF,同位角相等,GF∥BC,两直线平行,两直线平行.
17.解:(1)∵(40﹣2α)2+|β﹣20|=5,
∴20﹣2α=0,β﹣20=7,
∴α=β=20,
∴∠PFM=∠MFN=20°,∠EMF=20°,
∴∠EMF=∠MFN,
∴AB∥CD;
故答案为:20、20;
(2)∠FMN+∠GHF=180°;
理由:由(1)得AB∥CD,
∴∠MNF=∠PME,
∵∠MGH=∠MNF,
∴∠PME=∠MGH,
∴GH∥PN,
∴∠GHM=∠FMN,
∵∠GHF+∠GHM=180°,
∴∠FMN+∠GHF=180°;
(3)的值不变,;
理由:如图3中,作∠PEM1的平分线交M1Q的延长线于R,
∵AB∥CD,
∴∠PEM2=∠PFN,
∵∠PER=∠PEM5,∠PFQ=∠PFN,
∴∠PER=∠PFQ,
∴ER∥FQ,
∴∠FQM3=∠R,
设∠PER=∠REB=x,∠PM1R=∠RM1B=y,
则有:,
可得∠EPM6=2∠R,
∴∠EPM1=4∠FQM1,
∴=5.
18.解:(1)∵AE平分∠BAD(已知),
∴∠BAD=2∠1(角平分线的定义),
∵BE平分∠ABC(已知),
∴∠ABC=5∠2(角平分线的定义),
∴∠BAD+∠ABC=2∠7+2∠2(等量代换),
∵∠7+∠2=90°(已知),
∴∠BAD+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行).
故答案为:角平分线的定义;角平分线的定义;同旁内角互补.
(2)∵∠1+∠8+∠AEB=180°,∠1+∠2=90°,
∴∠AEB=90°=∠AEF+∠BEF,
∵∠AED+∠AEB+∠CEB=180°,
∴∠AED+∠CEB=90°,
∵AE平分∠DEF,
∴∠AED=∠AEF,
∴∠BEF=∠CEB(等角的余角相等)
∴BE平分∠CEF.
19.解:(1)AD∥EF,理由如下:
∵AB∥DG,
∴∠1=∠BAD,
∵∠1+∠8=180°,
∴∠BAD+∠2=180°,
∴AD∥EF;
(2)∵∠1+∠4=180°,∠2=145°,
∴∠1=35°,
∵DG是∠ADC的平分线,
∴∠ADC=7∠1=70°,
∴∠ADB=180°﹣∠ADC=110°,
∵AD∥EF,
∴∠EFB=∠ADB=110°,
∵∠BEF=180°﹣∠2=35°,
∴∠B=180°﹣∠EFB﹣∠BEF=180°﹣110°﹣35°=35°.
20.解:(1)平行,
∵AB∥CD,
∴∠B=∠BDE,
∵∠C=∠B,
∴∠C=∠BDE,
∴CF∥BD;
(2)∵CF∥BD,
∴∠ADB+∠FAD=180°,
∵∠ADB=106°,
∴∠FAD=74°,
∵AB是∠FAD的平分线,
∴∠FAB=37°,
∵CF∥BD,
∴∠B=∠FAB=37°.
21.解:(1)如图,∵∠1=∠2(已知),
∴a∥b(内错角相等,两直线平行),
∴∠2+∠4=180°(两直线平行,同旁内角互补),
∵∠3=65°(已知),
∴∠4=115°(补角的定义).
(2)根据题意,可画出图形如下:
由题意可知,∠AOM=60°,
∴∠AON=30°(余角的定义),
∵ON∥AC(已知),
∴∠AON+∠A=180°(两直线平行,同旁内角互补),
∵OA∥BC(已知),
∴∠A+∠ACB=180°(两直线平行,同旁内角互补),
∴∠AON=∠ACB=30°(同角的补角相等).
22.(1)证明:∵∠E=∠EMA,∠BQM=∠BMQ,
∴∠E=∠BQM,
∴EF∥BC;
(2)解:∵∠3+∠4=180°,∠4=∠MNF,
∴∠3+∠MNF=180°,
∴AB∥FP,
∴∠F+∠BAF=180°,
∵∠BAF=3∠F﹣20°,
∴∠F+6∠F﹣20°=180°,
解得∠F=50°,
∵AB∥FP,EF∥BC,
∴∠B=∠1,∠1=∠F,
∴∠B=∠F=50°.
23.解:(1)过点E作EF∥AB,
则有∠BEF=∠B,
∵AB∥CD,
∴EF∥CD,
∴∠FED=∠D,
∴∠BED=∠BEF+∠FED=∠B+∠D;
故答案为:∠B;EF;∠D;
(2)①如图1,过点E作EF∥AB,
有∠BEF=∠EBA.
∵AB∥CD,
∴EF∥CD.
∴∠FED=∠EDC.
∴∠BEF+∠FED=∠EBA+∠EDC.
即∠BED=∠EBA+∠EDC,
∵BE平分∠ABC,DE平分∠ADC,
∴∠EBA=∠ABC=30°∠ADC=35°,
∴∠BED=∠EBA+∠EDC=65°.
答:∠BED的度数为65°;
②如图3,过点E作EF∥AB,
有∠BEF+∠EBA=180°.
∴∠BEF=180°﹣∠EBA,
∵AB∥CD,
∴EF∥CD.
∴∠FED=∠EDC.
∴∠BEF+∠FED=180°﹣∠EBA+∠EDC.
即∠BED=180°﹣∠EBA+∠EDC,
∵BE平分∠ABC,DE平分∠ADC,
∴∠EBA=∠ABC=∠ADC=,
∴∠BED=180°﹣∠EBA+∠EDC=180°﹣+.
答:∠BED的度数为180°﹣.
24.(1)证明:如图1,∵∠AGE+∠DHE=180°.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠GMH=∠GMR+∠RMH=∠AGM+∠CHM.
(3)解:如图7,令∠AGM=2α,则∠N=2α,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点H作HT∥GN,
则∠MHT=∠N=6α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+7β,
∠CHG=∠CHM+∠MHT+∠GHT=β+2α+2β=3α+3β,
∵AB∥CD,
∴∠AGH+∠CHG=180°,
∴90°+α+2α+4β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
25.解:(1)AD∥EC.
理由:∵∠1=∠CDF,
∴AB∥CD,
∴∠2=∠CDA.
∵∠2+∠3=180°,
∴∠CDA+∠3=180°,
∴AD∥EC.
(2)∵CE⊥EF,
∴∠CEA=90°.
由(1)知AD∥EC,
∴∠DAF=∠CEA=90°.
∵∠7=140°,
∴∠CDA=180°﹣140°=40°,
∴∠2=∠CDA=40°,
∴∠FAB=90°﹣40°=50°
一.选择题(共6小题)
1.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠2=∠3,则b∥c D.若∠1+∠5=180°,则d∥e
2.如图a∥b,c与a相交,d与b相交
①若∠1=∠2,则∠3=∠4;
②若∠1+∠4=180°,则c∥d;
③∠4﹣∠2=∠3﹣∠1;
④∠1+∠2+∠3+∠4=360°,正确的有( )
A.①③④ B.①②③ C.①②④ D.②③
3.如图,已知∠1=∠2=∠3=50°,则∠4的度数为( )
A.50° B.100° C.130° D.150°
4.小明和小亮在研究一道数学题,如图EF⊥AB,CD⊥AB,D,G在AC上.
小明说:“如果∠CDG=∠BFE,则能得到∠AGD=∠ACB”;
小亮说:“连接FG,如果FG∥AB,则能得到∠GFC=∠ADG”.
则下列判断正确的是( )
A.小明说法正确,小亮说法错误
B.小明说法正确,小亮说法正确
C.小明说法错误,小亮说法正确
D.小明说法错误,小亮说法错误
5.如图,小敏在作业中的一道题:如图1,直线a,你有什么办法量出这两条直线所成的角的度数?小敏的做法是:如图2,画PC∥a,即直线a,b所成角的度数.其依据是( )
A.两直线平行,同位角相等
B.同旁内角互补,两直线平行
C.内错角相等,两直线平行
D.同位角相等,两直线平行
6.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容.则回答正确的是( )
已知:如图,∠BEC=∠B+∠C.
求证:AB∥CD.
证明:延长BE交※于点F,
则∠BEC=180°﹣∠FEC=◎+∠C.
又∠BEC=∠B+∠C,得∠B=▲.
故AB∥CD(@相等,两直线平行).
A.◎代表∠FEC B.@代表同位角
C.▲代表∠EFC D.※代表AB
二.填空题(共4小题)
7.如图1,为响应国家新能源建设,乐清市公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线),如图2,电池板AB与最大夹角时刻的太阳光线相垂直,要使AB∥CD,需将电池板CD逆时针旋转α度 .(0<α<90)
8.如图,已知∠1=∠2=∠3=50°,则∠4= .
9.已知三条不同的直线a、b、c在同一平面内,下列四句:
①如果a∥b,a⊥c,那么b⊥c,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c,c与a相交,那么b与c相交.
其中正确的是 .
10.一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动至图2位置的过程中,BC∥DE.则∠CAE其余符合条件的度数为 .
三.解答题(共15小题)
11.如图,B,C,D是不在同一直线上的三点,且∠CDE+∠BCD﹣∠ABC=180°.
(1)如图1,求证:AB∥DE;
(2)DG平分∠EDC,点P是DG上一点,过点P作射线PB;
①如图2,若PD∥BC,∠ABC=2∠3;(用含α的式子表示)
②如图3,若∠3+∠C=90°,并说明理由.
12.如图,AB∥CD,CH平分∠ACD交AB于点H
(1)求证:AE∥CH;
(2)若∠AHC=62°,求∠ACH的度数.
13.如图1,已AB∥CD,∠C=∠A.
(1)求证:AD∥BC;
(2)如图2,若点E是在平行线AB,CD内,探究∠BAE,∠CDE,并证明.
(3)如图3,若∠C=90°,且点E在线段BC上,射线DF在∠EDC的内部,且交BC于点M,∠AED+∠AEC=180°,
①直接写出∠AED与∠FDC的数量关系: .
②点P在射线DA上,且满足∠DEP=2∠F,∠DEA﹣∠PEA=,补全图形后,求∠EPD的度数.
14.如图,已知∠A=∠FEC,∠DEF=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠BDC=3∠B,求∠EFC的度数.
15.如图,AD∥BC,∠1=∠B
(1)求证:AB∥DE;
(2)AF与DC有什么位置关系?为什么?
(3)若∠B=68°,∠C=46°,求∠2的度数.
16.已知:如图,点E在BC上,BD⊥AC,垂足分别为D、F,点M、G在AB上,∠1=∠2.
求证:∠DMB+∠ABC=180°.
小勇在做上面这道题时用了以下推理过程.请帮他在横线上填写结论,在括号内填写推理依据.
证明:∵BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
∴∠BDC=90°,∠EFC=90° ( ).
∴∠BDC=∠EFC(等量代换).
∴ (同位角相等,两直线平行).
∴∠CBD=∠2 .
∵∠1=∠2(已知).
∴∠CBD=∠1 ( ).
∴ ( ).
∵∠AMD=∠AGF(已知).
∴GF∥MD(同位角相等,两直线平行).
∴BC∥MD ( ).
∴∠DMB+∠ABC=180° ( ).
17.已知,如图1,射线PE分别与直线AB,∠PFD的平分线与直线AB相交于点M,射线PM交CD于点N,∠EMF=β°,且(40﹣2α)2+|β﹣20|=0.
(1)α= ,β= ;直线AB与CD的位置关系是 ;
(2)如图2,若点G、H分别在射线MA和线段MF上,且∠MGH=∠PNF,并证明你的结论;
(3)若将图中的射线PM绕着端点P逆时针方向旋转(如图3),分别与AB、CD相交于点M1和点N1时,作∠PM1B的角平分线M1Q与射线FM相交于点Q,问在旋转的过程中的值是否改变?若不变;若变化,请说明理由.
18.如图,在四边形ABCD中,AE,点E在CD上,∠1+∠2=90°
(1)完成下面的说理过程解:
解:∵AE平分∠BAD(已知),
∴∠BAD=2∠1( ),
∵BE平分∠ABC(已知),
∴∠ABC=2∠2( ),
∴∠BAD+∠ABC=2∠1+2∠2( ),
∵∠1+∠2=90°(已知),
∴∠BAD+∠ABC=180°,
∴AD∥BC( ).
(2)若AE平分∠DEF,试说明BE平分∠CEF.
19.如图,E,G是分别是AB,AC上的点,F,连接EF,AD,如果AB∥DG,∠1+∠2=180°.
(1)判断AD与EF的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠2=145°,求∠B的度数.
20.如图,已知∠C=∠B,AB∥CD.
(1)试着先判断CF与BD所在的直线平行?请说明理由.
(2)如果AB是∠FAD的平分线,且∠ADB=106°,求∠B的度数.
21.(1)如图,已知∠1=∠2,∠3=65°
(2)一艘船从O处出发沿北偏东60°方向行驶至A,然后向正东方向行驶至C后又改变航向,朝与出发时相反的方向行驶至B.请画出该船的航线示意图
22.如图,已知点A在EF上,点P,∠E=∠EMA,∠BQM=∠BMQ.
(1)求证:EF∥BC;
(2)若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.
23.阅读下面材料:
小亮同学遇到这样一个问题:
已知:如图甲,AB∥CD,E为AB,连接BE,DE
求证:∠BED=∠B+∠D.
(1)小亮写出了该问题的证明,请你帮他把证明过程补充完整.
证明:过点E作EF∥AB,
则有∠BEF= .
∵AB∥CD,
∴ ∥ ,
∴∠FED= .
∴∠BED=∠BEF+∠FED=∠B+∠D.
(2)请你参考小亮思考问题的方法,解决问题:如图乙,
已知:直线a∥b,点A,B在直线a上,D在直线b上,连接AD,BE平分∠ABC,DE平分∠ADC,DE所在的直线交于点E.
①如图1,当点B在点A的左侧时,若∠ABC=60°,求∠BED的度数;
②如图2,当点B在点A的右侧时,设∠ABC=α,请你求出∠BED的度数(用含有α,β的式子表示).
24.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,点M在直线AB,CD之间,HM,求证:∠M=∠AGM+∠CHM;
(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,连接GN,若∠N=∠AGM∠FGN,求∠MHG的度数.
25.如图,已知∠1=∠CDF,∠2+∠3=180°.
(1)请你判断AD与EC的位置关系,并说明理由;
(2)若CE⊥EF,且∠3=140°,求∠FAB的度数.
参考答案
一.选择题(共6小题)
1.解:A、若a∥b,则a∥c,正确;
B、若∠1=∠2,利用了内错角相等,正确;
C、∠3=∠2,错误;
D、若∠1+∠6=180°,利用同旁内角互补,正确;
故选:C.
2.解:
①若∠1=∠2,则a∥e∥b,故此说法正确;
②若∠4+∠4=180°,由a∥b得到,则∠1=∠8;故此说法正确;
③由a∥b得到,∠5+∠4=180°,∠5+∠3+180°﹣∠4+180°﹣∠2=360°,故此说法正确;
④由③得,只有∠1+∠4=∠7+∠3=180°时.故此说法错误.
故选:B.
3.解:∵∠1=∠BFE=50°,
∴∠BFE=∠2=50°,
∴AB∥CD,
∴∠3=∠NEC,
∵∠NEC=180°﹣∠3=180°﹣50°=130°,
∴∠4=130°,
故选:C.
4.解:∵EF⊥AB,CD⊥AB,
∴CD∥EF,
若∠CDG=∠BFE,
∵∠BCD=∠BFE,
∴∠BCD=∠CDG,
∴DG∥BC,
∴∠AGD=∠ACB,故小明说法正确;
∵FG∥AB,
∴∠B=∠GFC,
故得不到∠GFC=∠ADG,故小亮说法错误,
故选:A.
5.解:根据两直线平行,同位角相等得到直线a和直线b的夹角与直线b和直线PC的夹角相等.
故选:A.
6.证明:延长BE交CD于点F,
则∠BEC=180°﹣∠FEC=∠EFC+∠C.
又∠BEC=∠B+∠C,得∠B=∠EFC.
故AB∥CD(内错角相等,两直线平行).
所以※代表CD,◎代表∠EFC,@代表内错角,
故选:C.
二.填空题(共4小题)
7.解:
∵EF⊥AB,
∴∠EFO=90°,
∵∠OEF=62°,
∴∠EOF=180°﹣90°﹣62°=28°,
∵AB∥CD,
∴∠MQD=∠EOF=28°,
∵要使AB∥CD,需将电池板CD逆时针旋转α度,
∴α°=48°﹣28°=20°,
故答案为:20.
8.解:∵∠1=∠2,∠4=∠5,
∴∠5=∠3,
∴b∥c,
∴∠3+∠6=180°,
∵∠6=50°,
∴∠6=130°,
∴∠4=130°.
故答案为:130°.
9.解:∵直线a,b,c在同一平面内,
∴①如果a∥b,a⊥c;
②如果b∥a,c∥a;
③如果b⊥a,c⊥a,故错误;
④如果b⊥a,c与a相交,故错误.
故正确的是①②.
故答案为:①②.
10.解:如图3,当BC∥DE时;
如图,当AE∥BC时;
如图,当DE∥AB(或AD∥BC)时;
如图,当DE∥AC时.
综上所述,旋转后两块三角板至少有一组边平行,
故答案为:60°或105°或135°.
三.解答题(共15小题)
11.解:(1)如图1,延长DC交AB于点F,
∵∠BFC=∠BCD﹣∠ABC,
∴∠CDE+∠BCD﹣∠ABC=180°,
即∠CDE+∠BFC=180°,
∴AB∥DE;
(2)①∵PD∥BC,
∴∠2=∠4,
又∵∠ABC=2∠3,∠ABC=∠5+∠2,
∴∠1=∠8=∠3=α,∠ABC=2α,
∵DG平分∠EDC,∠CDG+∠C=180°,
∴∠EDC+∠C=180°,①
∵∠CDE+∠BCD﹣∠ABC=180°,
即∠CDE+∠C﹣2α=180°,②
联立①②解得∠C=180°﹣2α;
②∠1=∠2,理由如下:
如图4,作CH平分∠C交DG于H,
∴∠4=∠5=∠BCD,
∵DG平分∠EDC,
∴∠CDG=∠EDC,
∴∠5+∠CDG=(∠BCD+∠EDC),
又∵∠CDE+∠BCD﹣∠ABC=180°,
∴∠5+∠CDG=(180°+∠ABC)=90°+,
∴∠PHC=90°+∠ABC,
∵∠3+∠C=90°,
∴∠3+∠7=90°,
∴∠PBC=360°﹣∠3﹣∠4﹣∠PHC=360°﹣90°﹣90°﹣∠ABC=180°﹣,
又∵∠PBC+∠2=180°,
∴∠2=∠ABC,
∴∠1=∠6.
12.(1)证明:∵AB∥CD,
∴∠FAB=∠FCD,
∵AE平分∠FAB,CH平分∠ACD,
∴∠FAE=∠FAB∠FCD,
∴∠FAE=∠FCH,
∴AE∥CH;
(2)∵AB∥CD,
∴∠AHC=∠HCD,
∵∠AHC=62°,
∴∠HCD=62°,
∵CH平分∠ACD,
∴∠ACH=∠HCD=62°.
13.(1)证明:AB∥CD,
∴∠A+∠D=180°,
∵∠C=∠A,
∴∠C+∠D=180°,
∴AD∥BC;
(2)∠BAE+∠CDE=∠AED,理由如下:
如图2,过点E作EF∥AB,
∵AB∥CD
∴AB∥CD∥EF
∴∠BAE=∠AEF,∠CDE=∠DEF
即∠BAE+∠EAD+∠CDE+∠DEF=180°
∴∠BAE+∠CDE=∠AED;
(3)①∠AED﹣∠FDC=45°;
∵∠AED+∠AEC=180°,∠AED+∠DEC+∠AEB=180°,
∴∠AEC=∠DEC+∠AEB,
∴∠AED=∠AEB,∠DEC=90°﹣2∠FDC,
∴3∠AED+(90°﹣2∠FDC)=180°,
∴∠AED﹣∠FDC=45°,
故答案为:∠AED﹣∠FDC=45°;
②如图3,
∵∠AED=∠F+∠FDE,∠AED﹣∠FDC=45°,
∴∠F=45°,
∴∠DEP=4∠F=90°,
∵∠DEA﹣∠PEA=∠DEB=,
∴∠PEA=∠AED,
∴∠DEP=∠PEA+∠AED=∠AED=90°,
∴∠AED=70°,
∵∠AED+∠AEC=180°,
∴∠DEC+2∠AED=180°,
∴∠DEC=40°,
∵AD∥BC,
∴∠ADE=∠DEC=40°,
在△PDE中,∠EPD=180°﹣∠DEP﹣∠AED=50°,
即∠EPD=50°.
14.解:(1)DE∥BC,理由如下:
∵∠A=∠FEC,
∴AB∥EF,
∴∠DEF=∠ADE,
∵∠DEF=∠B,
∴∠ADE=∠B,
∴DE∥BC;
(2)设∠B=x,则∠BDC=3∠B=3x,
∵DE∥BC,
∴∠ADE=∠B=x,
∵DE平分∠ADC,
∴∠ADC=7∠ADE=2x,
∴∠BDC+∠ADC=180°,
∴3x+8x=180°,
∴x=36°,
∴∠ADC=2x=72°,
∵AB∥EF,
∴∠EFC=∠ADC=72°.
15.(1)证明:∵AD∥BC(已知),
∴∠1=∠DEC(两直线平行,内错角相等),
∵∠1=∠B(已知),
∴∠DEC=∠B(等量代换),
∴AB∥DE(同位角相等,两直线平行);
(2)解:AF∥DC,
理由如下:
∵AB∥DE(已证),
∴∠5=∠AGD(两直线平行,内错角相等),
∵∠2=∠3(已知),
∴∠AGD=∠5(等量代换),
∴AF∥DC(内错角相等,两直线平行);
(3)∵AF∥DC,∠C=46°,
∴∠AFB=∠C=46°(两直线平行,同位角相等),
∵∠B=68°,∠2+∠B+∠AFB=180°,
∴∠2=180°﹣∠B﹣∠AFB=180°﹣46°﹣68°=66°.
16.证明:∵BD⊥AC,EF⊥AC、F(已知),
∴∠BDC=90°,∠EFC=90°( ),
∴∠BDC=∠EFC(等量代换),
∴BD∥EF(同位角相等,两直线平行),
∴∠CBD=∠2( 两直线平行 ),
∵∠1=∠2(已知),
∴∠CBD=∠1(等量代换),
∴GF∥BC(内错角相等,两直线平行 ),
∵∠AMD=∠AGF(已知),
∴GF∥MD(同位角相等,两直线平行),
∴BC∥MD(平行公理的推论),
∴∠DMB+∠ABC=180°(两直线平行,同旁内角互补),
故答案为:垂直的定义,BD∥EF,同位角相等,GF∥BC,两直线平行,两直线平行.
17.解:(1)∵(40﹣2α)2+|β﹣20|=5,
∴20﹣2α=0,β﹣20=7,
∴α=β=20,
∴∠PFM=∠MFN=20°,∠EMF=20°,
∴∠EMF=∠MFN,
∴AB∥CD;
故答案为:20、20;
(2)∠FMN+∠GHF=180°;
理由:由(1)得AB∥CD,
∴∠MNF=∠PME,
∵∠MGH=∠MNF,
∴∠PME=∠MGH,
∴GH∥PN,
∴∠GHM=∠FMN,
∵∠GHF+∠GHM=180°,
∴∠FMN+∠GHF=180°;
(3)的值不变,;
理由:如图3中,作∠PEM1的平分线交M1Q的延长线于R,
∵AB∥CD,
∴∠PEM2=∠PFN,
∵∠PER=∠PEM5,∠PFQ=∠PFN,
∴∠PER=∠PFQ,
∴ER∥FQ,
∴∠FQM3=∠R,
设∠PER=∠REB=x,∠PM1R=∠RM1B=y,
则有:,
可得∠EPM6=2∠R,
∴∠EPM1=4∠FQM1,
∴=5.
18.解:(1)∵AE平分∠BAD(已知),
∴∠BAD=2∠1(角平分线的定义),
∵BE平分∠ABC(已知),
∴∠ABC=5∠2(角平分线的定义),
∴∠BAD+∠ABC=2∠7+2∠2(等量代换),
∵∠7+∠2=90°(已知),
∴∠BAD+∠ABC=180°,
∴AD∥BC(同旁内角互补,两直线平行).
故答案为:角平分线的定义;角平分线的定义;同旁内角互补.
(2)∵∠1+∠8+∠AEB=180°,∠1+∠2=90°,
∴∠AEB=90°=∠AEF+∠BEF,
∵∠AED+∠AEB+∠CEB=180°,
∴∠AED+∠CEB=90°,
∵AE平分∠DEF,
∴∠AED=∠AEF,
∴∠BEF=∠CEB(等角的余角相等)
∴BE平分∠CEF.
19.解:(1)AD∥EF,理由如下:
∵AB∥DG,
∴∠1=∠BAD,
∵∠1+∠8=180°,
∴∠BAD+∠2=180°,
∴AD∥EF;
(2)∵∠1+∠4=180°,∠2=145°,
∴∠1=35°,
∵DG是∠ADC的平分线,
∴∠ADC=7∠1=70°,
∴∠ADB=180°﹣∠ADC=110°,
∵AD∥EF,
∴∠EFB=∠ADB=110°,
∵∠BEF=180°﹣∠2=35°,
∴∠B=180°﹣∠EFB﹣∠BEF=180°﹣110°﹣35°=35°.
20.解:(1)平行,
∵AB∥CD,
∴∠B=∠BDE,
∵∠C=∠B,
∴∠C=∠BDE,
∴CF∥BD;
(2)∵CF∥BD,
∴∠ADB+∠FAD=180°,
∵∠ADB=106°,
∴∠FAD=74°,
∵AB是∠FAD的平分线,
∴∠FAB=37°,
∵CF∥BD,
∴∠B=∠FAB=37°.
21.解:(1)如图,∵∠1=∠2(已知),
∴a∥b(内错角相等,两直线平行),
∴∠2+∠4=180°(两直线平行,同旁内角互补),
∵∠3=65°(已知),
∴∠4=115°(补角的定义).
(2)根据题意,可画出图形如下:
由题意可知,∠AOM=60°,
∴∠AON=30°(余角的定义),
∵ON∥AC(已知),
∴∠AON+∠A=180°(两直线平行,同旁内角互补),
∵OA∥BC(已知),
∴∠A+∠ACB=180°(两直线平行,同旁内角互补),
∴∠AON=∠ACB=30°(同角的补角相等).
22.(1)证明:∵∠E=∠EMA,∠BQM=∠BMQ,
∴∠E=∠BQM,
∴EF∥BC;
(2)解:∵∠3+∠4=180°,∠4=∠MNF,
∴∠3+∠MNF=180°,
∴AB∥FP,
∴∠F+∠BAF=180°,
∵∠BAF=3∠F﹣20°,
∴∠F+6∠F﹣20°=180°,
解得∠F=50°,
∵AB∥FP,EF∥BC,
∴∠B=∠1,∠1=∠F,
∴∠B=∠F=50°.
23.解:(1)过点E作EF∥AB,
则有∠BEF=∠B,
∵AB∥CD,
∴EF∥CD,
∴∠FED=∠D,
∴∠BED=∠BEF+∠FED=∠B+∠D;
故答案为:∠B;EF;∠D;
(2)①如图1,过点E作EF∥AB,
有∠BEF=∠EBA.
∵AB∥CD,
∴EF∥CD.
∴∠FED=∠EDC.
∴∠BEF+∠FED=∠EBA+∠EDC.
即∠BED=∠EBA+∠EDC,
∵BE平分∠ABC,DE平分∠ADC,
∴∠EBA=∠ABC=30°∠ADC=35°,
∴∠BED=∠EBA+∠EDC=65°.
答:∠BED的度数为65°;
②如图3,过点E作EF∥AB,
有∠BEF+∠EBA=180°.
∴∠BEF=180°﹣∠EBA,
∵AB∥CD,
∴EF∥CD.
∴∠FED=∠EDC.
∴∠BEF+∠FED=180°﹣∠EBA+∠EDC.
即∠BED=180°﹣∠EBA+∠EDC,
∵BE平分∠ABC,DE平分∠ADC,
∴∠EBA=∠ABC=∠ADC=,
∴∠BED=180°﹣∠EBA+∠EDC=180°﹣+.
答:∠BED的度数为180°﹣.
24.(1)证明:如图1,∵∠AGE+∠DHE=180°.
∴∠BGF+∠DHE=180°,
∴AB∥CD;
(2)证明:如图2,过点M作MR∥AB,
又∵AB∥CD,
∴AB∥CD∥MR.
∴∠GMR=∠AGM,∠HMR=∠CHM.
∴∠GMH=∠GMR+∠RMH=∠AGM+∠CHM.
(3)解:如图7,令∠AGM=2α,则∠N=2α,
∵射线GH是∠BGM的平分线,
∴,
∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,
∵,
∴,
∴∠FGN=2β,
过点H作HT∥GN,
则∠MHT=∠N=6α,∠GHT=∠FGN=2β,
∴∠GHM=∠MHT+∠GHT=2α+7β,
∠CHG=∠CHM+∠MHT+∠GHT=β+2α+2β=3α+3β,
∵AB∥CD,
∴∠AGH+∠CHG=180°,
∴90°+α+2α+4β=180°,
∴α+β=30°,
∴∠GHM=2(α+β)=60°.
25.解:(1)AD∥EC.
理由:∵∠1=∠CDF,
∴AB∥CD,
∴∠2=∠CDA.
∵∠2+∠3=180°,
∴∠CDA+∠3=180°,
∴AD∥EC.
(2)∵CE⊥EF,
∴∠CEA=90°.
由(1)知AD∥EC,
∴∠DAF=∠CEA=90°.
∵∠7=140°,
∴∠CDA=180°﹣140°=40°,
∴∠2=∠CDA=40°,
∴∠FAB=90°﹣40°=50°
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
