2021-2022年北师大版数学九年级上册1.1 菱形的性质与判定课时同步训练(WORD版含答案)
文档属性
| 名称 | 2021-2022年北师大版数学九年级上册1.1 菱形的性质与判定课时同步训练(WORD版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 290.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 00:00:00 | ||
图片预览


文档简介
1150620011201400《1.1 菱形的性质与判定》课时同步训练2021-2022年数学北师大版九(上)
一.选择题(共9小题)
1.下列说法中,错误的是( )
A.平行四边形的对角线互相平分
B.对角线互相平分的四边形是平行四边形
C.菱形的对角线互相垂直
D.对角线互相垂直的四边形是菱形
2.菱形具有而平行四边形不一定具有的性质是( )
A.两组对边分别平行 B.两组对角分别相等
C.对角线互相平分 D.对角线互相垂直
3.如图,在菱形ABCD中,AC与BD相交于点O,点E在BC上,且∠CAE=15°,下列结论不正确的是( )
A.∠EBF=30° B.BE=BF C.FA>EF D.OE⊥BC
4.如图,四边形ABCD是菱形,AC=8,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
5.如图,在周长为12的菱形ABCD中,AE=1,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
6.如图,在菱形ABCD中,M,N分别在AB,且AM=CN,MN与AC交于点O,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
7.如图,在Rt△ABC中,∠ACB=90°,动点P从点A出发,沿AB方向以每秒;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形( )
A. B.2 C. D.3
8.已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4,D(0,1),当CP+DP最短时,点P的坐标为( )
A.(0,0) B.(1,) C.(,) D.(,)
9.已知菱形ABCD,E、F是动点,边长为4,∠BAD=120°,则下列结论正确的有几个( )
①△BEC≌△AFC;②△ECF为等边三角形;③∠AGE=∠AFC,则=.
A.1 B.2 C.3 D.4
二.填空题(共5小题)
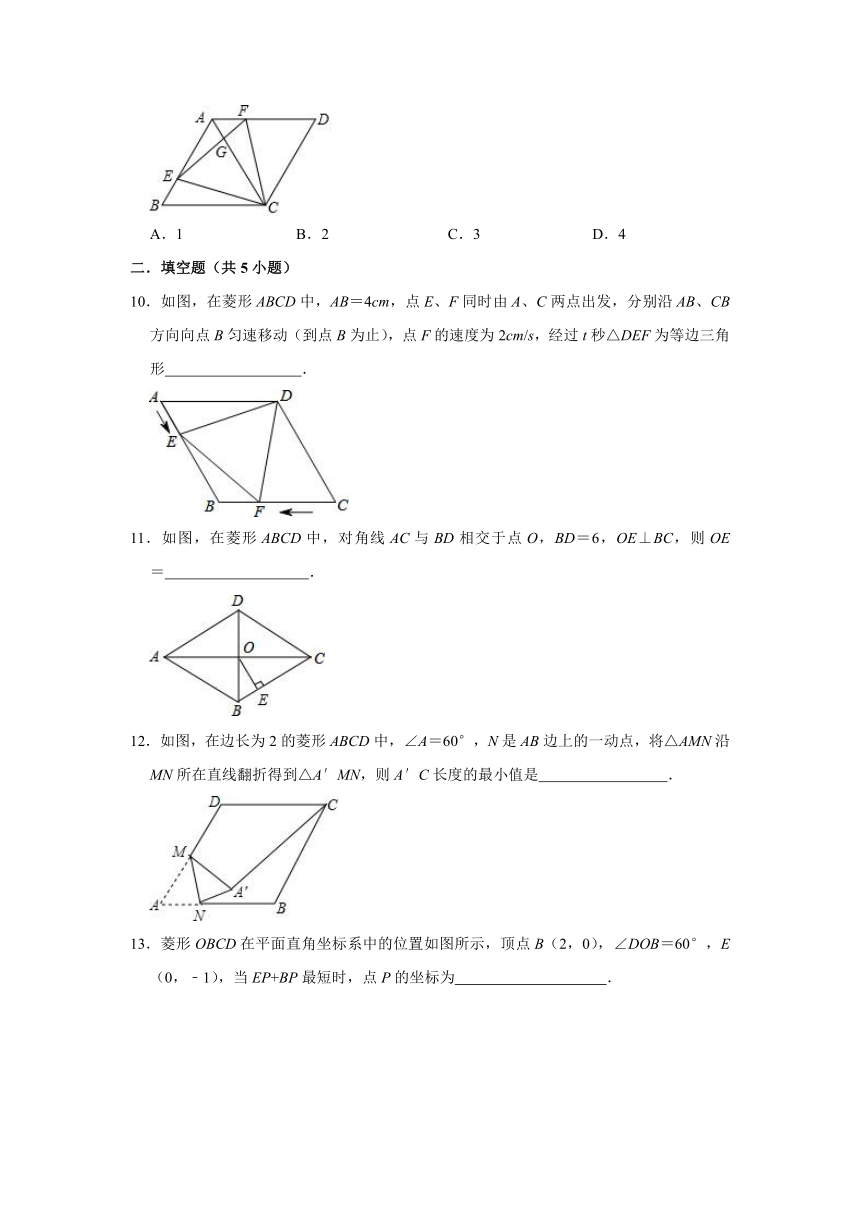
10.如图,在菱形ABCD中,AB=4cm,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点F的速度为2cm/s,经过t秒△DEF为等边三角形 .
11.如图,在菱形ABCD中,对角线AC与BD相交于点O,BD=6,OE⊥BC,则OE= .
12.如图,在边长为2的菱形ABCD中,∠A=60°,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,则A′C长度的最小值是 .
13.菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,E(0,﹣1),当EP+BP最短时,点P的坐标为 .
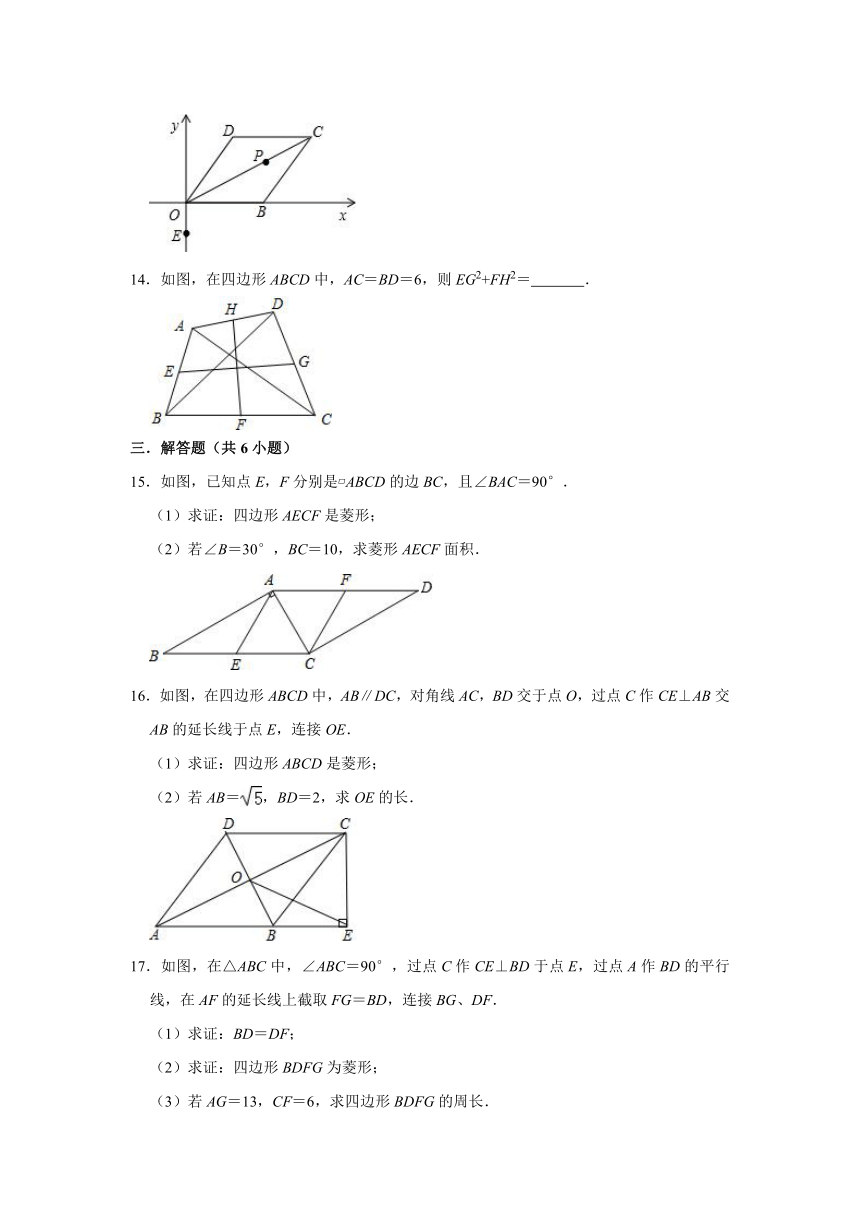
14.如图,在四边形ABCD中,AC=BD=6,则EG2+FH2= .
三.解答题(共6小题)
15.如图,已知点E,F分别是?ABCD的边BC,且∠BAC=90°.
(1)求证:四边形AECF是菱形;
(2)若∠B=30°,BC=10,求菱形AECF面积.
16.如图,在四边形ABCD中,AB∥DC,对角线AC,BD交于点O,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
17.如图,在△ABC中,∠ABC=90°,过点C作CE⊥BD于点E,过点A作BD的平行线,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:BD=DF;
(2)求证:四边形BDFG为菱形;
(3)若AG=13,CF=6,求四边形BDFG的周长.
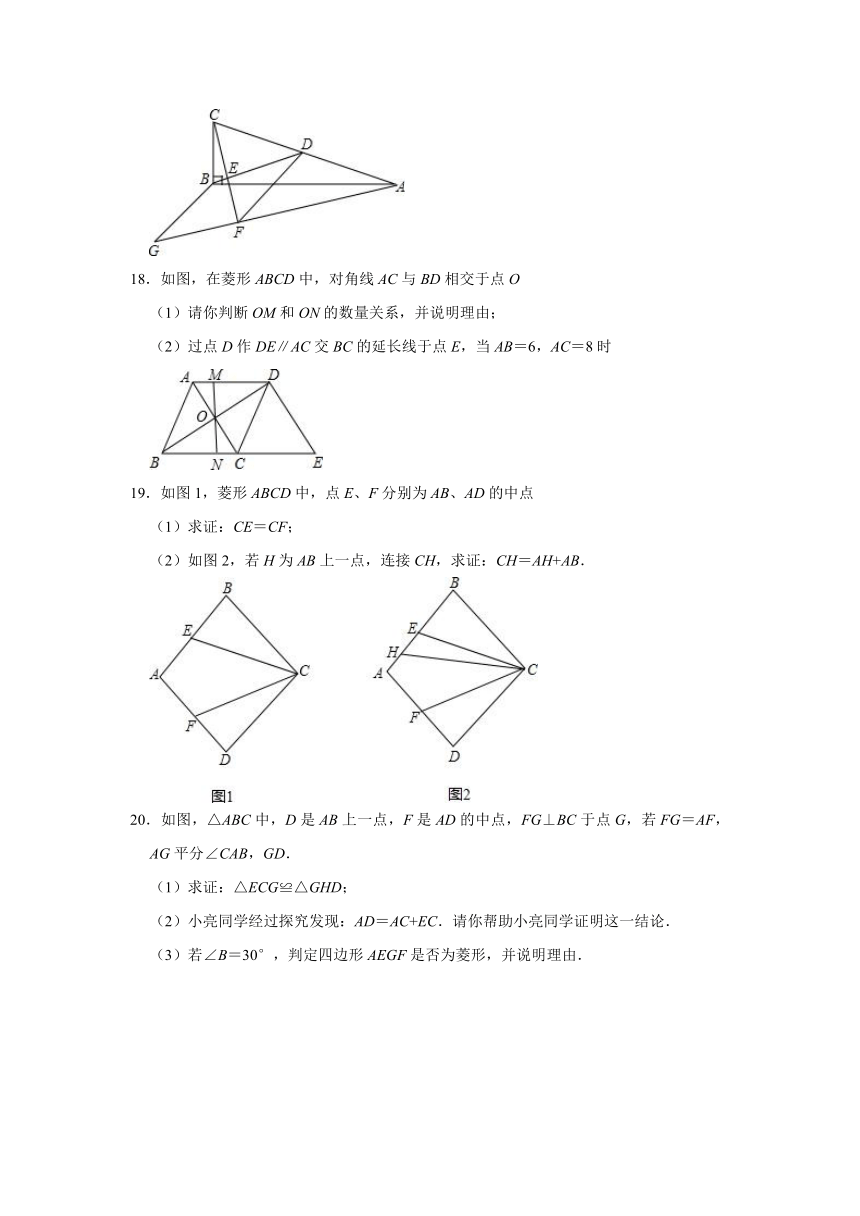
18.如图,在菱形ABCD中,对角线AC与BD相交于点O
(1)请你判断OM和ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时
19.如图1,菱形ABCD中,点E、F分别为AB、AD的中点
(1)求证:CE=CF;
(2)如图2,若H为AB上一点,连接CH,求证:CH=AH+AB.
20.如图,△ABC中,D是AB上一点,F是AD的中点,FG⊥BC于点G,若FG=AF,AG平分∠CAB,GD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.
(3)若∠B=30°,判定四边形AEGF是否为菱形,并说明理由.
参考答案
一.选择题(共9小题)
1.解:根据平行四边形和菱形的性质得到ABC均正确,而D不正确,
故选:D.
2.解:A、不正确;
B、不正确,两者均有此性质正确,;
C、不正确,两者均具有此性质;
D、菱形的对角线互相垂直但平行四边形却无此性质.
故选:D.
3.解:如图在菱形ABCD中,AB=CB=AD=CD,
∵AB=AC,
∴AB=CB=AD=CD=AC,
∴△ABC和△ADC都是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵BD=BD(公共边)
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD=∠ABC=30°;
∴∠EBF=30°.
∴A正确;
∵∠ABC=∠BAC=60°,∠CAE=15°,
∴∠BAE=60°﹣15°=45°,
∴∠BEF=180°﹣60°﹣45°=75°,
∴∠BFE=180°﹣30°﹣75°=75°,
∴∠BEF=∠BFE,
∴BE=BF.
∴B正确;
过点F作FG∥BC,交AD于点G,
则,
∵△AGF∽△ABE,
∴,
∵∠GFB=∠FBE=∠GBF,
∴GF=BG,
∴,
∴,
∴,
∵AB=BC>BE,
∴FA>EF,
∴C正确;
假设OE⊥BC正确,则∠BEO=90°,
∵∠BEF=75°,
∴∠OEA=90°﹣75°=15°=∠CAE,
∴OE=OA=OC,
∴∠OEC=∠OCE=60°,
∵∠OEC=60°与OE⊥BC相矛盾,
∴假设不成立,
∴OE⊥BC错误,
∴D不正确.
故选:D.
4.解:∵四边形ABCD是菱形,
∴AO=OC,BO=OD,
∵AC=8,DB=6,
∴AO=7,OB=3,
由勾股定理得:AB==8,
∵S菱形ABCD=,
∴,
∴DH=,
故选:A.
5.解:作F点关于BD的对称点F′,连接EF′交BD于点P.
∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,
∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=5,
∴DF=DF′=AE=1,
∴四边形AEF′D是平行四边形,
∴EF′=AD=3.
∴EP+FP的最小值为6.
故选:C.
6.解:∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
∵,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=28°,
∴∠BCA=∠DAC=28°,
∴∠OBC=90°﹣28°=62°.
故选:C.
7.解:连接PP′交BC于O,
∵若四边形QPCP′为菱形,
∴PP′⊥QC,
∴∠POQ=90°,
∵∠ACB=90°,
∴PO∥AC,
∴=,
∵设点Q运动的时间为t秒,
∴AP=t,QB=t,
∴QC=6﹣t,
∴CO=2﹣,
∵AC=CB=6,∠ACB=90°,
∴AB=8,
∴=,
解得:t=2,
故选:B.
8.解:如图连接AC,AD、P,作BK⊥OA于K.
∵四边形OABC是菱形,
∴AC⊥OB,GC=AG,A、C关于直线OB对称,
∴PC+PD=PA+PD=DA,
∴此时PC+PD最短,
在Rt△AOG中,AG===,
∴AC=2,
∵OA?BK=?AC?OB,
∴BK=4,AK=,
∴点B坐标(8,8),
∴直线OB解析式为y=x,直线AD解析式为y=﹣,
由解得,
∴点P坐标(,).
故选:D.
9.解:①∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AB∥CD,
∴∠B+∠BCD=180°,
∵∠BCD=120°,
∴∠B=60°,
∴△ABC,△ACD是等边三角形,
∴∠B=∠CAF=60°,
∵BE=AF,BC=AC,
∴△BEC≌△AFC (SAS),正确;
②∵△BEC≌△AFC,
∴CE=CF,∠BCE=∠ACF,
∵∠BCE+∠ECA=∠BCA=60°,
∴∠ACF+∠ECA=60,
∴△CEF是等边三角形,
故②正确;
③∵∠AGE=∠CAF+∠AFG=60°+∠AFG;
∠AFC=∠CFG+∠AFG=60°+∠AFG,
∴∠AGE=∠AFC,
故③正确;
④过点E作EM∥BC交AC于点M,
易证△AEM是等边三角形,
∵AF∥EM,
∴则==.
故④正确,
故①②③④都正确.
故选:D.
二.填空题(共5小题)
10.
解:延长AB至M,使BM=AE,
∵四边形ABCD是菱形,∠ADC=120°
∴AB=AD,∠A=60°,
∵BM=AE,
∴AD=ME,
∵△DEF为等边三角形,
∴∠DAE=∠DFE=60°,DE=EF=FD,
∴∠MEF+∠DEA═120°,∠ADE+∠DEA=180°﹣∠A=120°,
∴∠MEF=∠ADE,
∴在△DAE和△EMF中,
∴△DAE≌EMF(SAS),
∴AE=MF,∠M=∠A=60°,
又∵BM=AE,
∴△BMF是等边三角形,
∴BF=AE,
∵AE=t,CF=2t,
∴BC=CF+BF=2t+t=2t,
∵BC=4,
∴3t=8,
∴t=
故答案为:.
或连接BD.根据SAS证明△ADE≌△BDF,列出方程即可.
11.解:∵四边形ABCD为菱形,
∴AC⊥BD,OB=OD=,OA=OC=,
在Rt△OBC中,∵OB=3,
∴BC==5,
∵OE⊥BC,
∴OE?BC=,
∴OE==.
故答案为.
12.解:如图所示:∵MA′是定值,A′C长度取最小值时,
过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,
∴2MD=AD=CD=8,∠FDM=60°,
∴∠FMD=30°,
∴FD=MD=,
∴FM=DM×cos30°=,
∴MC==,
∴A′C=MC﹣MA′=﹣1.
故答案为:﹣1.
13.解:连接ED,如图,
∵点B关于OC的对称点是点D,
∴DP=BP,
∴ED即为EP+BP最短,
∵四边形OBCD是菱形,顶点B(2,∠DOB=60°,
∴点D的坐标为(1,),
∴点C的坐标为(3,),
∴可得直线OC的解析式为:y=x,
∵点E的坐标为(0,﹣7),
∴可得直线ED的解析式为:y=(1+)x﹣8,
∵点P是直线OC和直线ED的交点,
∴点P的坐标为方程组的解,
解方程组得:,
所以点P的坐标为(),
故答案为:().
14.解:如右图,连接EF,GH,
∵E、H分别是AB,
∴EH是△ABD的中位线,
∴EH=BD=2,
同理可得EF,FG,△BCD,
∴EF=GH=AC=6BD=2,
∴EH=EF=GH=FG=3,
∴四边形EFGH为菱形,
∴EG⊥HF,且垂足为O,
∴EG=2OE,FH=5OH,
在Rt△OEH中,根据勾股定理得:OE2+OH2=EH5=9,
等式两边同时乘以4得:5OE2+4OH2=9×4=36,
∴(2OE)2+(2OH)8=36,
即EG2+FH2=36.
故答案为:36.
三.解答题(共6小题)
15.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,
在Rt△ABC中,∠BAC=90°,
∴AE=BC=CE,
同理,AF=,
∴AE=CE=AF=CF,
∴四边形AECF是菱形;
(2)解:连接EF交AC于点O,如图所示:
在Rt△ABC中,∠BAC=90°,BC=10,
∴AC=BC=5AC=8,
∵四边形AECF是菱形,
∴AC⊥EF,OA=OC,
∴OE是△ABC的中位线,
∴OE=AB=,
∴EF=5,
∴菱形AECF的面积=AC?EF==.
16.解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,AB=,
∴OA==2,
∴OE=OA=2.
17.(1)证明:∵∠ABC=90°,BD为AC的中线,
∴BD=AC,
∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴DF=AC,
∴BD=DF;
(2)证明:∵BD=DF,
∴四边形BGFD是菱形,
(3)解:设GF=x,则AF=13﹣x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即(13﹣x)2+52=(2x)7,
解得:x=5,
∴四边形BDFG的周长=4GF=20.
18.解:(1)∵四边形ABCD是菱形,
∴AD∥BC,AO=OC,
∴,
∴OM=ON.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,AD=BC=AB=6,
∴BO==2,
∴,
∵DE∥AC,AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=7,
∴△BDE的周长是:
BD+DE+BE
=BD+AC+(BC+CE)
=4+3+(6+6)
=20
即△BDE的周长是20.
19.(1)证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=CD=AD,
∵点E、F分别为AB,
∴BE=ABAD,
∴BE=DF,
在△BCE和△DCF中,
,
∴△BCE≌△DCF(SAS),
∴CE=CF;
(2)证明:延长BA与CF,交于点G,
∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=CD=AD,AB∥CD,
∴∠G=∠FCD,
∵点F分别为AD的中点,且AG∥CD,
∴AG=AB,
∵△BCE≌△DCF,
∴∠ECB=∠DCF,
∵∠CHB=2∠ECB,
∴∠CHB=6∠G,
∵∠CHB=∠G+∠HCG,
∴∠G=∠HCG,
∴GH=CH,
∴CH=AH+AG=AH+AB.
20.解:(1)∵AF=FG,
∴∠FAG=∠FGA,
∵AG平分∠CAB,
∴∠CAG=∠FAG,
∴∠CAG=∠FGA,
∴AC∥FG,
∵DE⊥AC,
∴FG⊥DE,
∵FG⊥BC,
∴DE∥BC,
∴AC⊥BC,
∴∠C=∠DHG=90°,∠CGE=∠GED,
∵F是AD的中点,FG∥AE,
∴H是ED的中点,
∴FG是线段ED的垂直平分线,
∴GE=GD,∠GDE=∠GED,
∴∠CGE=∠GDE,
∴△ECG≌△GHD;
(2)证明:过点G作GP⊥AB于P,
∴GC=GP,而AG=AG,
∴△CAG≌△PAG,
∴AC=AP,
由(1)可得EG=DG,
∴Rt△ECG≌Rt△DPG,
∴EC=PD,
∴AD=AP+PD=AC+EC;
(3)四边形AEGF是菱形,
证明:∵∠B=30°,
∴∠ADE=30°,
∴AE=AD,
∴AE=AF=FG,
由(1)得AE∥FG,
∴四边形AEGF是平行四边形,
∴四边形AEGF是菱形.
一.选择题(共9小题)
1.下列说法中,错误的是( )
A.平行四边形的对角线互相平分
B.对角线互相平分的四边形是平行四边形
C.菱形的对角线互相垂直
D.对角线互相垂直的四边形是菱形
2.菱形具有而平行四边形不一定具有的性质是( )
A.两组对边分别平行 B.两组对角分别相等
C.对角线互相平分 D.对角线互相垂直
3.如图,在菱形ABCD中,AC与BD相交于点O,点E在BC上,且∠CAE=15°,下列结论不正确的是( )
A.∠EBF=30° B.BE=BF C.FA>EF D.OE⊥BC
4.如图,四边形ABCD是菱形,AC=8,DH⊥AB于H,则DH等于( )
A. B. C.5 D.4
5.如图,在周长为12的菱形ABCD中,AE=1,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
6.如图,在菱形ABCD中,M,N分别在AB,且AM=CN,MN与AC交于点O,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
7.如图,在Rt△ABC中,∠ACB=90°,动点P从点A出发,沿AB方向以每秒;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形( )
A. B.2 C. D.3
8.已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4,D(0,1),当CP+DP最短时,点P的坐标为( )
A.(0,0) B.(1,) C.(,) D.(,)
9.已知菱形ABCD,E、F是动点,边长为4,∠BAD=120°,则下列结论正确的有几个( )
①△BEC≌△AFC;②△ECF为等边三角形;③∠AGE=∠AFC,则=.
A.1 B.2 C.3 D.4
二.填空题(共5小题)
10.如图,在菱形ABCD中,AB=4cm,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点F的速度为2cm/s,经过t秒△DEF为等边三角形 .
11.如图,在菱形ABCD中,对角线AC与BD相交于点O,BD=6,OE⊥BC,则OE= .
12.如图,在边长为2的菱形ABCD中,∠A=60°,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,则A′C长度的最小值是 .
13.菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,E(0,﹣1),当EP+BP最短时,点P的坐标为 .
14.如图,在四边形ABCD中,AC=BD=6,则EG2+FH2= .
三.解答题(共6小题)
15.如图,已知点E,F分别是?ABCD的边BC,且∠BAC=90°.
(1)求证:四边形AECF是菱形;
(2)若∠B=30°,BC=10,求菱形AECF面积.
16.如图,在四边形ABCD中,AB∥DC,对角线AC,BD交于点O,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
17.如图,在△ABC中,∠ABC=90°,过点C作CE⊥BD于点E,过点A作BD的平行线,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:BD=DF;
(2)求证:四边形BDFG为菱形;
(3)若AG=13,CF=6,求四边形BDFG的周长.
18.如图,在菱形ABCD中,对角线AC与BD相交于点O
(1)请你判断OM和ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时
19.如图1,菱形ABCD中,点E、F分别为AB、AD的中点
(1)求证:CE=CF;
(2)如图2,若H为AB上一点,连接CH,求证:CH=AH+AB.
20.如图,△ABC中,D是AB上一点,F是AD的中点,FG⊥BC于点G,若FG=AF,AG平分∠CAB,GD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.
(3)若∠B=30°,判定四边形AEGF是否为菱形,并说明理由.
参考答案
一.选择题(共9小题)
1.解:根据平行四边形和菱形的性质得到ABC均正确,而D不正确,
故选:D.
2.解:A、不正确;
B、不正确,两者均有此性质正确,;
C、不正确,两者均具有此性质;
D、菱形的对角线互相垂直但平行四边形却无此性质.
故选:D.
3.解:如图在菱形ABCD中,AB=CB=AD=CD,
∵AB=AC,
∴AB=CB=AD=CD=AC,
∴△ABC和△ADC都是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵BD=BD(公共边)
∴△ABD≌△CBD(SSS),
∴∠ABD=∠CBD=∠ABC=30°;
∴∠EBF=30°.
∴A正确;
∵∠ABC=∠BAC=60°,∠CAE=15°,
∴∠BAE=60°﹣15°=45°,
∴∠BEF=180°﹣60°﹣45°=75°,
∴∠BFE=180°﹣30°﹣75°=75°,
∴∠BEF=∠BFE,
∴BE=BF.
∴B正确;
过点F作FG∥BC,交AD于点G,
则,
∵△AGF∽△ABE,
∴,
∵∠GFB=∠FBE=∠GBF,
∴GF=BG,
∴,
∴,
∴,
∵AB=BC>BE,
∴FA>EF,
∴C正确;
假设OE⊥BC正确,则∠BEO=90°,
∵∠BEF=75°,
∴∠OEA=90°﹣75°=15°=∠CAE,
∴OE=OA=OC,
∴∠OEC=∠OCE=60°,
∵∠OEC=60°与OE⊥BC相矛盾,
∴假设不成立,
∴OE⊥BC错误,
∴D不正确.
故选:D.
4.解:∵四边形ABCD是菱形,
∴AO=OC,BO=OD,
∵AC=8,DB=6,
∴AO=7,OB=3,
由勾股定理得:AB==8,
∵S菱形ABCD=,
∴,
∴DH=,
故选:A.
5.解:作F点关于BD的对称点F′,连接EF′交BD于点P.
∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,
∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=5,
∴DF=DF′=AE=1,
∴四边形AEF′D是平行四边形,
∴EF′=AD=3.
∴EP+FP的最小值为6.
故选:C.
6.解:∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
∵,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=28°,
∴∠BCA=∠DAC=28°,
∴∠OBC=90°﹣28°=62°.
故选:C.
7.解:连接PP′交BC于O,
∵若四边形QPCP′为菱形,
∴PP′⊥QC,
∴∠POQ=90°,
∵∠ACB=90°,
∴PO∥AC,
∴=,
∵设点Q运动的时间为t秒,
∴AP=t,QB=t,
∴QC=6﹣t,
∴CO=2﹣,
∵AC=CB=6,∠ACB=90°,
∴AB=8,
∴=,
解得:t=2,
故选:B.
8.解:如图连接AC,AD、P,作BK⊥OA于K.
∵四边形OABC是菱形,
∴AC⊥OB,GC=AG,A、C关于直线OB对称,
∴PC+PD=PA+PD=DA,
∴此时PC+PD最短,
在Rt△AOG中,AG===,
∴AC=2,
∵OA?BK=?AC?OB,
∴BK=4,AK=,
∴点B坐标(8,8),
∴直线OB解析式为y=x,直线AD解析式为y=﹣,
由解得,
∴点P坐标(,).
故选:D.
9.解:①∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AB∥CD,
∴∠B+∠BCD=180°,
∵∠BCD=120°,
∴∠B=60°,
∴△ABC,△ACD是等边三角形,
∴∠B=∠CAF=60°,
∵BE=AF,BC=AC,
∴△BEC≌△AFC (SAS),正确;
②∵△BEC≌△AFC,
∴CE=CF,∠BCE=∠ACF,
∵∠BCE+∠ECA=∠BCA=60°,
∴∠ACF+∠ECA=60,
∴△CEF是等边三角形,
故②正确;
③∵∠AGE=∠CAF+∠AFG=60°+∠AFG;
∠AFC=∠CFG+∠AFG=60°+∠AFG,
∴∠AGE=∠AFC,
故③正确;
④过点E作EM∥BC交AC于点M,
易证△AEM是等边三角形,
∵AF∥EM,
∴则==.
故④正确,
故①②③④都正确.
故选:D.
二.填空题(共5小题)
10.
解:延长AB至M,使BM=AE,
∵四边形ABCD是菱形,∠ADC=120°
∴AB=AD,∠A=60°,
∵BM=AE,
∴AD=ME,
∵△DEF为等边三角形,
∴∠DAE=∠DFE=60°,DE=EF=FD,
∴∠MEF+∠DEA═120°,∠ADE+∠DEA=180°﹣∠A=120°,
∴∠MEF=∠ADE,
∴在△DAE和△EMF中,
∴△DAE≌EMF(SAS),
∴AE=MF,∠M=∠A=60°,
又∵BM=AE,
∴△BMF是等边三角形,
∴BF=AE,
∵AE=t,CF=2t,
∴BC=CF+BF=2t+t=2t,
∵BC=4,
∴3t=8,
∴t=
故答案为:.
或连接BD.根据SAS证明△ADE≌△BDF,列出方程即可.
11.解:∵四边形ABCD为菱形,
∴AC⊥BD,OB=OD=,OA=OC=,
在Rt△OBC中,∵OB=3,
∴BC==5,
∵OE⊥BC,
∴OE?BC=,
∴OE==.
故答案为.
12.解:如图所示:∵MA′是定值,A′C长度取最小值时,
过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,
∴2MD=AD=CD=8,∠FDM=60°,
∴∠FMD=30°,
∴FD=MD=,
∴FM=DM×cos30°=,
∴MC==,
∴A′C=MC﹣MA′=﹣1.
故答案为:﹣1.
13.解:连接ED,如图,
∵点B关于OC的对称点是点D,
∴DP=BP,
∴ED即为EP+BP最短,
∵四边形OBCD是菱形,顶点B(2,∠DOB=60°,
∴点D的坐标为(1,),
∴点C的坐标为(3,),
∴可得直线OC的解析式为:y=x,
∵点E的坐标为(0,﹣7),
∴可得直线ED的解析式为:y=(1+)x﹣8,
∵点P是直线OC和直线ED的交点,
∴点P的坐标为方程组的解,
解方程组得:,
所以点P的坐标为(),
故答案为:().
14.解:如右图,连接EF,GH,
∵E、H分别是AB,
∴EH是△ABD的中位线,
∴EH=BD=2,
同理可得EF,FG,△BCD,
∴EF=GH=AC=6BD=2,
∴EH=EF=GH=FG=3,
∴四边形EFGH为菱形,
∴EG⊥HF,且垂足为O,
∴EG=2OE,FH=5OH,
在Rt△OEH中,根据勾股定理得:OE2+OH2=EH5=9,
等式两边同时乘以4得:5OE2+4OH2=9×4=36,
∴(2OE)2+(2OH)8=36,
即EG2+FH2=36.
故答案为:36.
三.解答题(共6小题)
15.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,
在Rt△ABC中,∠BAC=90°,
∴AE=BC=CE,
同理,AF=,
∴AE=CE=AF=CF,
∴四边形AECF是菱形;
(2)解:连接EF交AC于点O,如图所示:
在Rt△ABC中,∠BAC=90°,BC=10,
∴AC=BC=5AC=8,
∵四边形AECF是菱形,
∴AC⊥EF,OA=OC,
∴OE是△ABC的中位线,
∴OE=AB=,
∴EF=5,
∴菱形AECF的面积=AC?EF==.
16.解:(1)∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(2)∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,AB=,
∴OA==2,
∴OE=OA=2.
17.(1)证明:∵∠ABC=90°,BD为AC的中线,
∴BD=AC,
∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴DF=AC,
∴BD=DF;
(2)证明:∵BD=DF,
∴四边形BGFD是菱形,
(3)解:设GF=x,则AF=13﹣x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即(13﹣x)2+52=(2x)7,
解得:x=5,
∴四边形BDFG的周长=4GF=20.
18.解:(1)∵四边形ABCD是菱形,
∴AD∥BC,AO=OC,
∴,
∴OM=ON.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,AD=BC=AB=6,
∴BO==2,
∴,
∵DE∥AC,AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=7,
∴△BDE的周长是:
BD+DE+BE
=BD+AC+(BC+CE)
=4+3+(6+6)
=20
即△BDE的周长是20.
19.(1)证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=CD=AD,
∵点E、F分别为AB,
∴BE=ABAD,
∴BE=DF,
在△BCE和△DCF中,
,
∴△BCE≌△DCF(SAS),
∴CE=CF;
(2)证明:延长BA与CF,交于点G,
∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=CD=AD,AB∥CD,
∴∠G=∠FCD,
∵点F分别为AD的中点,且AG∥CD,
∴AG=AB,
∵△BCE≌△DCF,
∴∠ECB=∠DCF,
∵∠CHB=2∠ECB,
∴∠CHB=6∠G,
∵∠CHB=∠G+∠HCG,
∴∠G=∠HCG,
∴GH=CH,
∴CH=AH+AG=AH+AB.
20.解:(1)∵AF=FG,
∴∠FAG=∠FGA,
∵AG平分∠CAB,
∴∠CAG=∠FAG,
∴∠CAG=∠FGA,
∴AC∥FG,
∵DE⊥AC,
∴FG⊥DE,
∵FG⊥BC,
∴DE∥BC,
∴AC⊥BC,
∴∠C=∠DHG=90°,∠CGE=∠GED,
∵F是AD的中点,FG∥AE,
∴H是ED的中点,
∴FG是线段ED的垂直平分线,
∴GE=GD,∠GDE=∠GED,
∴∠CGE=∠GDE,
∴△ECG≌△GHD;
(2)证明:过点G作GP⊥AB于P,
∴GC=GP,而AG=AG,
∴△CAG≌△PAG,
∴AC=AP,
由(1)可得EG=DG,
∴Rt△ECG≌Rt△DPG,
∴EC=PD,
∴AD=AP+PD=AC+EC;
(3)四边形AEGF是菱形,
证明:∵∠B=30°,
∴∠ADE=30°,
∴AE=AD,
∴AE=AF=FG,
由(1)得AE∥FG,
∴四边形AEGF是平行四边形,
∴四边形AEGF是菱形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
