上海市嘉定区2019-2020学年七年级下学期期末数学试卷(word版含解析)
文档属性
| 名称 | 上海市嘉定区2019-2020学年七年级下学期期末数学试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 296.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 13:33:42 | ||
图片预览



文档简介
2019-2020学年上海市嘉定区七年级(下)期末数学试卷
一、选择题:(本大题共6题,每题3分,满分18分)
1.下列各数:3.14,﹣,,π,5.3,0.2020020002……(它的位数无限且相邻两个2之间“0”的个数依次加1个),其中无理数有( )
A.1个 B.2个 C.3个 D.4个
2.下列各式中,正确的是( )
A.(﹣a)﹣2=a2 B.a?(﹣a)2=﹣a3
C.a3÷(﹣a)2=﹣a D.(﹣a3)2=a6
3.已知点A(m﹣1,m+4)在x轴上,则点A的坐标是( )
A.(0,5) B.(﹣5,0) C.(0,3) D.(﹣3,0)
4.如图,将三角板的直角顶点放在直尺的一边上,如果∠1=70°,那么∠2的度数为( )
A.10° B.15° C.20° D.25°
5.下列说法中,正确的是( )
A.腰对应相等的两个等腰三角形全等
B.等腰三角形角平分线与中线重合
C.底边和顶角分别对应相等的两个等腰三角形全等
D.形状相同的两个三角形全等
6.现有1cm、3cm、5cm、6cm长的四根木棒,任选其中三根组成一个三角形,那么可以组成三角形的个数是( )
A.1 B.2 C.3 D.4
二、填空题:(本大题共14题,每题2分,满分28分)
7.(2分)实数36的算术平方根是 .
8.(2分)把表示成幂的形式是 .
9.(2分)计算:()4+= .
10.(2分)比较大小:﹣ ﹣3(填“>”、“<”、“=”).
11.(2分)近似数1.2567×105有 个有效数字.
12.(2分)人体中成熟的红细胞平均直径为0.00077厘米,将数字0.00077用科学记数法表示为 .
13.(2分)与点P(﹣2,3)关于x轴对称的点的横坐标是 .
14.(2分)如图,一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是 .
15.(2分)△ABC的三个内角的度数之比是1:3:5,如果按角分类,那么△ABC是 三角形.
16.(2分)如图:已知AB=CD,使△ABO≌△CDO,还需添加一个条件,你添加的条件是 .(只需一个,不添加辅助线)
17.(2分)如图,在等腰△ABC中,AB=AC,点O是△ABC内一点,且OB=OC,联结AO并延长,交边BC于点D.如果BD=3,那么BC的值为 .
18.(2分)已知△ABC≌△A'B'C',等腰△ABC的周长为14cm,BC=6cm,那么△A'B'C'的底边长等于 .
19.(2分)如图,将直角三角形(∠ACB为直角)沿线段CD折叠使B落在B'处,若∠ACB'=50°,则∠ACD的度数为 .
20.(2分)如图是一组密码的一部分,为了保密,许多情况下采用不同的密码.请你运用所学知识,找到破译的“钥匙”.目前,据此“钥匙”已破译出“动脑思考”的真实意思是“装好收获”.请破译“正在做题”真实意思是 .
三、简答题:(本大题共5题,每题6分,满分30分)
21.(6分)计算:﹣12019+()﹣3+()2019?(﹣4)2019﹣(3﹣π)0.
22.(6分)利用幂的性质计算:(25×75)÷14(结果表示为幂的形式).
23.(6分)如图,已知∠A的两边与∠D的两边分别平行,且∠D比∠A的2倍多30°,求∠D的度数.
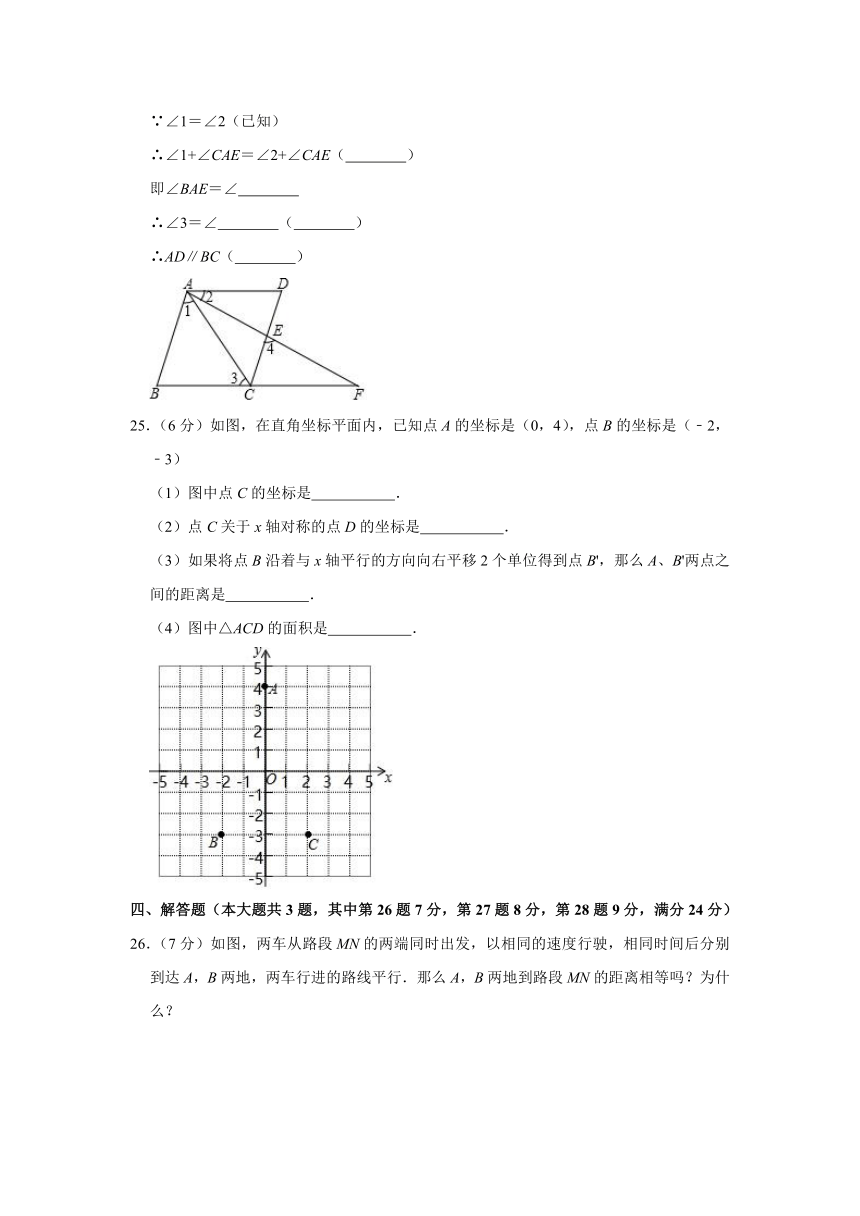
24.(6分)阅读并填空.已知:如图,线BCF、线AEF是直线,AB∥CD,∠1=∠2,∠3=∠4.试说明AD∥BC.
解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAE=∠2+∠CAE( )
即∠BAE=∠
∴∠3=∠ ( )
∴AD∥BC( )
25.(6分)如图,在直角坐标平面内,已知点A的坐标是(0,4),点B的坐标是(﹣2,﹣3)
(1)图中点C的坐标是 .
(2)点C关于x轴对称的点D的坐标是 .
(3)如果将点B沿着与x轴平行的方向向右平移2个单位得到点B',那么A、B'两点之间的距离是 .
(4)图中△ACD的面积是 .
四、解答题(本大题共3题,其中第26题7分,第27题8分,第28题9分,满分24分)
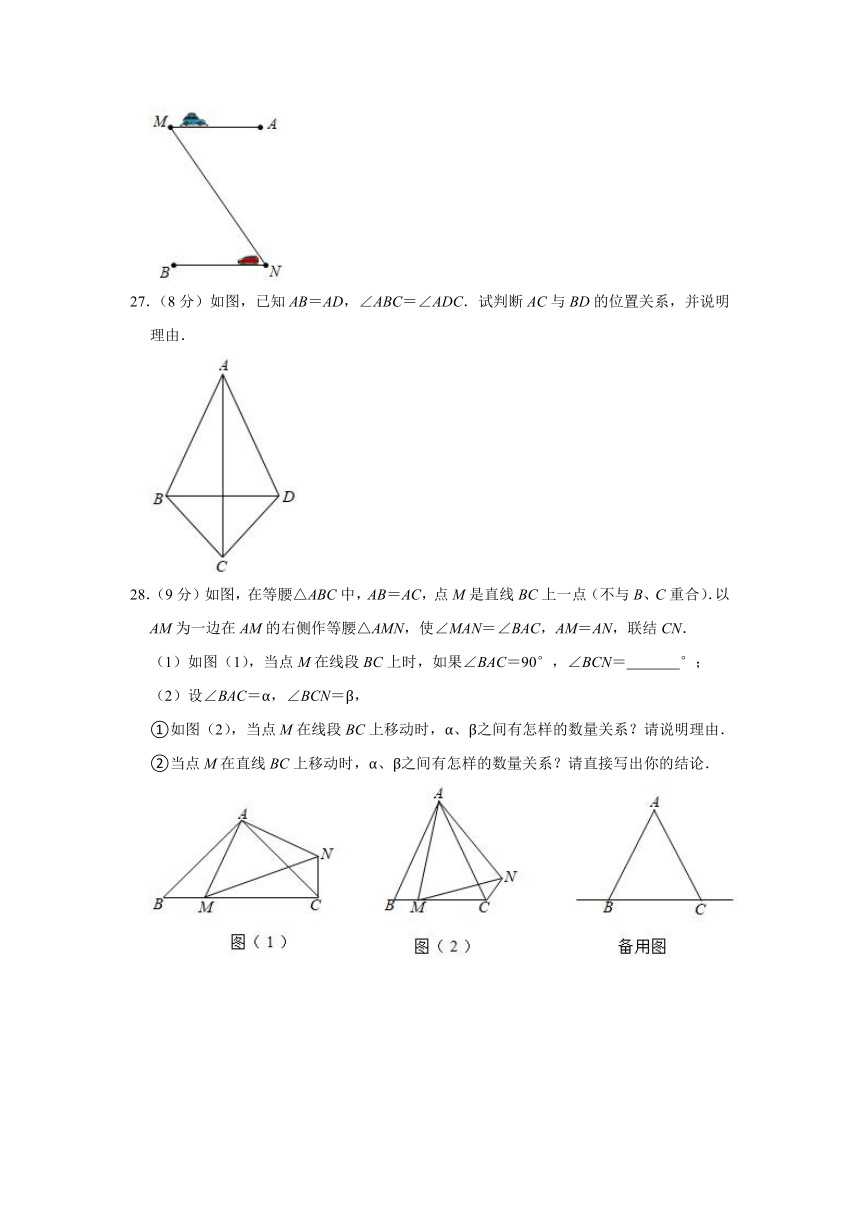
26.(7分)如图,两车从路段MN的两端同时出发,以相同的速度行驶,相同时间后分别到达A,B两地,两车行进的路线平行.那么A,B两地到路段MN的距离相等吗?为什么?
27.(8分)如图,已知AB=AD,∠ABC=∠ADC.试判断AC与BD的位置关系,并说明理由.
28.(9分)如图,在等腰△ABC中,AB=AC,点M是直线BC上一点(不与B、C重合).以AM为一边在AM的右侧作等腰△AMN,使∠MAN=∠BAC,AM=AN,联结CN.
(1)如图(1),当点M在线段BC上时,如果∠BAC=90°,∠BCN= °;
(2)设∠BAC=α,∠BCN=β,
①如图(2),当点M在线段BC上移动时,α、β之间有怎样的数量关系?请说明理由.
②当点M在直线BC上移动时,α、β之间有怎样的数量关系?请直接写出你的结论.
2019-2020学年上海市嘉定区七年级(下)期末数学试卷
参考答案与试题解析
一、选择题:(本大题共6题,每题3分,满分18分)
1.下列各数:3.14,﹣,,π,5.3,0.2020020002……(它的位数无限且相邻两个2之间“0”的个数依次加1个),其中无理数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据无理数的定义求解即可.
【解答】解:,π,0.2020020002……(它的位数无限且相邻两个2之间“0”的个数依次加1个)是无理数,共有3个,
故选:C.
2.下列各式中,正确的是( )
A.(﹣a)﹣2=a2 B.a?(﹣a)2=﹣a3
C.a3÷(﹣a)2=﹣a D.(﹣a3)2=a6
【分析】分别根据负整数指数幂的定义,同底数幂的乘法法则,同底数幂的除法法则以及幂的乘方运算法则逐一判断即可.
【解答】解:A.(﹣a)﹣2=,故本选项不符合题意;
B.a?(﹣a)2=a3,故本选项不符合题意;
C.a3÷(﹣a)2=a,故本选项不符合题意;
D.(﹣a3)2=a6,故本选项符合题意;
故选:D.
3.已知点A(m﹣1,m+4)在x轴上,则点A的坐标是( )
A.(0,5) B.(﹣5,0) C.(0,3) D.(﹣3,0)
【分析】直接利用x轴上点的坐标特点得出m的值,即可得出答案.
【解答】解:∵A(m﹣1,m+4)在x轴上,
∴m+4=0,
解得:m=﹣4,
∴m﹣1=﹣5,
∴点A的坐标是:(﹣5,0).
故选:B.
4.如图,将三角板的直角顶点放在直尺的一边上,如果∠1=70°,那么∠2的度数为( )
A.10° B.15° C.20° D.25°
【分析】利用平行线的性质可得∠3的度数,再利用平角定义可得∠2的度数.
【解答】解:∵a∥b,
∴∠1=∠3=70°,
∵∠4=90°,
∴∠2=180°﹣90°﹣70°=20°,
故选:C.
5.下列说法中,正确的是( )
A.腰对应相等的两个等腰三角形全等
B.等腰三角形角平分线与中线重合
C.底边和顶角分别对应相等的两个等腰三角形全等
D.形状相同的两个三角形全等
【分析】根据全等三角形的判定判断即可.
【解答】解:A、腰对应相等的两个等腰三角形不一定全等,因为角不一定相等,选项错误,不符合题意;
B、等腰三角形顶角的角平分线与底边的中线重合,选项错误,不符合题意;
C、底边和顶角分别对应相等的两个等腰三角形全等,利用ASA可得全等,选项正确,符合题意;
D、形状、大小相同的两个三角形全等,选项错误,不符合题意;
故选:C.
6.现有1cm、3cm、5cm、6cm长的四根木棒,任选其中三根组成一个三角形,那么可以组成三角形的个数是( )
A.1 B.2 C.3 D.4
【分析】从4条线段里任取3条线段组合,可有4种情况,看哪种情况不符合三角形三边关系,舍去即可.
【解答】解:四条木棒的所有组合:1,3,5和1,3,6和1,5,6和3,5,6;
只有3,5,6能组成三角形.
故选:A.
二、填空题:(本大题共14题,每题2分,满分28分)
7.(2分)实数36的算术平方根是 6 .
【分析】根据算术平方根的定义即可作答.
【解答】解:∵62=36,
∴36的算术平方根是6.
8.(2分)把表示成幂的形式是 .
【分析】根据分数指数幂即可求出答案.
【解答】解:.
故答案为:.
9.(2分)计算:()4+= 6 .
【分析】直接利用二次根式的性质进而分别计算得出答案.
【解答】解:原式=4+2
=6.
故答案为:6.
10.(2分)比较大小:﹣ < ﹣3(填“>”、“<”、“=”).
【分析】先把3化成,再与进行比较,即可得出结果.
【解答】解:∵3=,
∴>,
∴>3,
∴﹣<﹣3,
故答案为:<.
11.(2分)近似数1.2567×105有 5 个有效数字.
【分析】科学记数法的一般形式为a×10n,其中,1≤|a|<10,n为整数数位减1,有效数字应是a×10n中a的有效数字,即乘号前面的所有数字.
【解答】解:1.2567×105有1、2、5、6、7共5个有效数字;
故答案为5.
12.(2分)人体中成熟的红细胞平均直径为0.00077厘米,将数字0.00077用科学记数法表示为 7.7×10﹣4 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.00077=7.7×10﹣4.
故答案为:7.7×10﹣4.
13.(2分)与点P(﹣2,3)关于x轴对称的点的横坐标是 ﹣2 .
【分析】直接利用关于x轴对称点的性质,横坐标不变,纵坐标互为相反数,进而得出答案.
【解答】解:点P(﹣2,3)关于x轴对称的点的横坐标是﹣2.
故答案为:﹣2.
14.(2分)如图,一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是 105° .
【分析】先根据AD∥BC求出∠3的度数,再根据AB∥CD即可得出结论.
【解答】解:如图,∵AD∥BC,∠1=75°,
∴∠3=∠1=75°,
∵AB∥CD,
∴∠2=180°﹣∠3=180°﹣75°=105°.
故答案为:105°.
15.(2分)△ABC的三个内角的度数之比是1:3:5,如果按角分类,那么△ABC是 钝角 三角形.
【分析】已知三角形三个内角的度数之比,可以设一份为k°,根据三角形的内角和等于180°列方程求三个内角的度数,从而确定三角形的形状.
【解答】解:设一份为k°,则三个内角的度数分别为k°,3k°,5k°.
则k°+3k°+5k°=180°,
解得k=20,
∴5k°=100°,
所以这个三角形是钝角三角形.
故答案为:钝角.
16.(2分)如图:已知AB=CD,使△ABO≌△CDO,还需添加一个条件,你添加的条件是 ∠A=∠C .(只需一个,不添加辅助线)
【分析】由图形可知∠AOB=∠COD,结合条件,根据全等三角形的判定方法填写答案即可.
【解答】解:
∵AB=CD,且∠AOB=∠COD,
∴当∠B=∠D或∠A=∠C时,满足AAS,可证明△ABO≌△CDO,
故答案为:∠A=∠C(∠B=∠D).
17.(2分)如图,在等腰△ABC中,AB=AC,点O是△ABC内一点,且OB=OC,联结AO并延长,交边BC于点D.如果BD=3,那么BC的值为 6 .
【分析】证△ABO≌△ACO(SAS),得出∠BAO=∠CAO,由等腰三角形的性质得出CD=BD=3,即可得出答案.
【解答】解:∵AB=AC,OB=OC,
∴∠ABC=∠ACB,∠OBC=∠OCB,
∴∠ABO=∠ACO,
在△ABO和△ACO中,,
∴△ABO≌△ACO(SAS),
∴∠BAO=∠CAO,
∵AB=AC
∴CD=BD=3,
∴BC=2BD=6;
故答案为:6.
18.(2分)已知△ABC≌△A'B'C',等腰△ABC的周长为14cm,BC=6cm,那么△A'B'C'的底边长等于 4cm或2cm .
【分析】根据全等三角形的性质得出AB=A′B′,BC=B′C′,AC=A′C′,分为两种情况,求出即可.
【解答】解:∵△ABC≌△A′B′C′,
∴AB=A′B′,BC=B′C′,AC=A′C′,
分为两种情况:
①当BC是底边时,腰AB=AC,A′B′=A′C′,
∵△ABC≌△A′B′C′,
∴AB=AC=A′B′=A′C′,
∵等腰△ABC的周长为14cm,BC=6cm,
∴△A′B′C′中一定有一条底边B′C′的长是4cm,
②BC是腰时,腰是6cm,
∵等腰△ABC的周长为14cm,
∴△A′B′C′中一定有一条底边的长是14﹣6﹣6=2(cm),
即底边长是4cm或2cm,
故答案为:4cm或2cm.
19.(2分)如图,将直角三角形(∠ACB为直角)沿线段CD折叠使B落在B'处,若∠ACB'=50°,则∠ACD的度数为 20° .
【分析】根据翻折的性质可知:∠BCD=∠B′CD,又∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+60°=150°,继而即可求出∠BCD的值,又∠ACD+∠BCD=∠ACB=90°,继而即可求出∠ACD的度数.
【解答】解:∵△B′CD是由△BCD翻折得到的,
∴∠BCD=∠B′CD,
又∵∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+50°=140°,
∴∠BCD=70°,
又∵∠ACD+∠BCD=∠ACB=90°,
∴∠ACD=20°.
故答案为:20°.
20.(2分)如图是一组密码的一部分,为了保密,许多情况下采用不同的密码.请你运用所学知识,找到破译的“钥匙”.目前,据此“钥匙”已破译出“动脑思考”的真实意思是“装好收获”.请破译“正在做题”真实意思是 “我爱数学” .
【分析】根据题意可以发现对应字之间的规律,从而可以解答本题.
【解答】解:由题意可得,
“动脑思考”的真实意思是“装好收获”.“动”所对应的字为“装”,是“动”字先向右平移一个单位,再向上平移两个得到的“装”,其他各个字对应也是这样得到的,
∴“正在做题”的真实意思是“我爱数学”,
故答案为:“我爱数学”.
三、简答题:(本大题共5题,每题6分,满分30分)
21.(6分)计算:﹣12019+()﹣3+()2019?(﹣4)2019﹣(3﹣π)0.
【分析】根据根据有理数的乘方的定义,负整数指数幂的定义,积的乘方运算法则以及任何非零数的零次幂等于1计算即可.
【解答】解:原式=﹣1+
=﹣1+8﹣12019﹣1
=﹣1+8﹣1﹣1
=5.
22.(6分)利用幂的性质计算:(25×75)÷14(结果表示为幂的形式).
【分析】先根据积的乘方运算法则化简,再根据幂的乘方运算法则以及同底数幂的除法法则计算即可.
【解答】解:(25×75)÷14
=
=
=
=.
23.(6分)如图,已知∠A的两边与∠D的两边分别平行,且∠D比∠A的2倍多30°,求∠D的度数.
【分析】利用平行线的性质可得出∠A+∠D=180°,结合∠D比∠A的2倍多30°,即可求出∠D的度数.
【解答】解:∵AB∥DE,
∴∠1=∠A,
∵AC∥DF,
∴∠1+∠D=180°,
∴∠A+∠D=180°①,
∵∠D=2∠A+30°②,
解①②组成的方程组得∠D=130°.
24.(6分)阅读并填空.已知:如图,线BCF、线AEF是直线,AB∥CD,∠1=∠2,∠3=∠4.试说明AD∥BC.
解:∵AB∥CD(已知)
∴∠4=∠ BAE ( 两直线平行,同位角相等 )
∵∠3=∠4(已知)
∴∠3=∠ BAE ( 等量代换 )
∵∠1=∠2(已知)
∴∠1+∠CAE=∠2+∠CAE( 等式的性质 )
即∠BAE=∠ DAC
∴∠3=∠ DAC ( 等量代换 )
∴AD∥BC( 同错角相等,两直线平行 )
【分析】由AB∥CD得∠4=∠BAE,根据等量代换,等式的性质得∠3=∠DAC,最后由内错角相等,两直平行判定直线AD∥BC.
【解答】解:如图所示:
∵AB∥CD,
∴∠4=∠BAE(两直线平行,同位角相等),
又∵∠3=∠4,
∴∠3=∠BAE(等量代换),
又∵∠1=∠2,
∴∠1+∠CAE=∠2+∠CAE(角的和差),
∴∠BAE=∠DAC,
∴∠3=∠DAC(等量代换),
∴AD∥BC(内错角相等,两直线平行),
故答案为:BAE,两直线平行,同位角相等;BAE,等量代换,
等式的性质,DAC,DAC,等量代换,同错角相等,两直线平行.
25.(6分)如图,在直角坐标平面内,已知点A的坐标是(0,4),点B的坐标是(﹣2,﹣3)
(1)图中点C的坐标是 (2,﹣3) .
(2)点C关于x轴对称的点D的坐标是 (2,3) .
(3)如果将点B沿着与x轴平行的方向向右平移2个单位得到点B',那么A、B'两点之间的距离是 7 .
(4)图中△ACD的面积是 6 .
【分析】(1)根据平面直角坐标系可直接写出C点坐标;
(2)根据关于x轴对称的点的坐标特点:横坐标不变,纵坐标互为相反数可得D点坐标;
(3)根据点的平移:横坐标,右移加,左移减;纵坐标,上移加,下移减可得B′点坐标,进而得到答案;
(4)根据三角形的面积公式可得答案.
【解答】解:(1)图中点C的坐标是(2,﹣3).
(2)点C关于x轴对称的点D的坐标是(2,3).
(3)如果将点B沿着与x轴平行的方向向右平移2个单位得到点B'(﹣2+2,﹣3),即(0,﹣3),那么A、B'两点之间的距离是:4﹣(﹣3)=7.
(4)图中△ACD的面积:=.
故答案为:(1)(2,﹣3);(2)(2,3);(3)7;(4)6.
四、解答题(本大题共3题,其中第26题7分,第27题8分,第28题9分,满分24分)
26.(7分)如图,两车从路段MN的两端同时出发,以相同的速度行驶,相同时间后分别到达A,B两地,两车行进的路线平行.那么A,B两地到路段MN的距离相等吗?为什么?
【分析】要判断A,B两地到路段MN的距离是否相等,可以由条件证明△AEM≌△BFN,再根据全等三角形的性质就可以的得出结论.
【解答】解:A,B两地到路段MN的距离相等.
理由:∵AE⊥MN,BF⊥MN,
∴∠AFN=∠AEM=90°.
∵AM∥BN,
∴∠M=∠N.
在△AEM和△BFN中,
,
∴△AEM≌△BFN(AAS),
∴AE=BF.
∴A,B两地到路段MN的距离相等.
27.(8分)如图,已知AB=AD,∠ABC=∠ADC.试判断AC与BD的位置关系,并说明理由.
【分析】AC与BD垂直,理由为:由AB=AD,利用等边对等角得到一对角相等,利用等式性质得到∠BDC=∠DBC,利用等角对等边得到DC=BC,利用SSS得到三角形ABC与三角形ADC全等,利用全等三角形对应角相等得到∠DAC=∠BAC,再利用三线合一即可得证.
【解答】解:AC⊥BD,理由为:
∵AB=AD(已知),
∴∠ADB=∠ABD(等边对等角),
∵∠ABC=∠ADC(已知),
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB(等式性质),即∠BDC=∠DBC,
∴DC=BC(等角对等边),
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠DAC=∠BAC(全等三角形的对应角相等),
又∵AB=AD,
∴AC⊥BD(等腰三角形三线合一).
28.(9分)如图,在等腰△ABC中,AB=AC,点M是直线BC上一点(不与B、C重合).以AM为一边在AM的右侧作等腰△AMN,使∠MAN=∠BAC,AM=AN,联结CN.
(1)如图(1),当点M在线段BC上时,如果∠BAC=90°,∠BCN= 90 °;
(2)设∠BAC=α,∠BCN=β,
①如图(2),当点M在线段BC上移动时,α、β之间有怎样的数量关系?请说明理由.
②当点M在直线BC上移动时,α、β之间有怎样的数量关系?请直接写出你的结论.
【分析】(1)由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAM≌△CAN,可得∠ABC=∠ACN=45°,可求∠BCN的度数;
(2)①由“SAS”可证△ABM≌△ACN得出∠ABM=∠ACN,再用三角形的内角和即可得出结论;
②分两种情况画出图形,由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和与外角的性质即可得出结论.
【解答】解:(1)∵AB=AC,∠BAC=90°,
则∠ABC=∠ACB=45°,
∵∠MAN=∠BAC,
∴∠BAM=∠CAN,且AB=AC,AM=AN,
∴△BAM≌△CAN(SAS),
∴∠ABC=∠ACN=45°,
∴∠BCN=∠ACB+∠ACN=90°,
故答案为:90;
(2)①α+β=180°,理由如下:
∵∠BAC=∠MAN,
∴∠BAC﹣∠MAC=∠MAN﹣∠MAC.
即∠BAM=∠CAN.
在△ABM与△ACN中,
,
∴△ABM≌△ACN(SAS),
∴∠B=∠ACN.
∴∠B+∠ACB=∠ACN+∠ACB.
∵∠ACN+∠ACB=β,
∴∠B+∠ACB=β,
∵α+∠B+∠ACB=180°,
∴α+β=180°;
②当点M在BC的延长线上时,α+β=180°,如图:
理由如下:∵∠BAC=∠MAN,
∴∠BAM=∠CAN,
在△ABD和△ACE中,
,
∴△ABM≌△ACN(SAS),
∴∠ABM=∠ACN,
在△ABC中,∠BAC+∠ABM+∠ACB=180°,
∴∠BAC+∠ACN+∠ACB=∠BAC+∠BCN=180°,
即:α+β=180°.
当点M在CB的延长线上时,α=β,如图:
理由如下:∵∠BAC=∠MAN,
∴∠BAM=∠CAN,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(SAS),
∴∠ABM=∠ACN,
∵∠ABM=∠α+∠ACB,∠ACN=∠β+∠ACB,
∴α=β.
综上,α+β=180°或α=β.
一、选择题:(本大题共6题,每题3分,满分18分)
1.下列各数:3.14,﹣,,π,5.3,0.2020020002……(它的位数无限且相邻两个2之间“0”的个数依次加1个),其中无理数有( )
A.1个 B.2个 C.3个 D.4个
2.下列各式中,正确的是( )
A.(﹣a)﹣2=a2 B.a?(﹣a)2=﹣a3
C.a3÷(﹣a)2=﹣a D.(﹣a3)2=a6
3.已知点A(m﹣1,m+4)在x轴上,则点A的坐标是( )
A.(0,5) B.(﹣5,0) C.(0,3) D.(﹣3,0)
4.如图,将三角板的直角顶点放在直尺的一边上,如果∠1=70°,那么∠2的度数为( )
A.10° B.15° C.20° D.25°
5.下列说法中,正确的是( )
A.腰对应相等的两个等腰三角形全等
B.等腰三角形角平分线与中线重合
C.底边和顶角分别对应相等的两个等腰三角形全等
D.形状相同的两个三角形全等
6.现有1cm、3cm、5cm、6cm长的四根木棒,任选其中三根组成一个三角形,那么可以组成三角形的个数是( )
A.1 B.2 C.3 D.4
二、填空题:(本大题共14题,每题2分,满分28分)
7.(2分)实数36的算术平方根是 .
8.(2分)把表示成幂的形式是 .
9.(2分)计算:()4+= .
10.(2分)比较大小:﹣ ﹣3(填“>”、“<”、“=”).
11.(2分)近似数1.2567×105有 个有效数字.
12.(2分)人体中成熟的红细胞平均直径为0.00077厘米,将数字0.00077用科学记数法表示为 .
13.(2分)与点P(﹣2,3)关于x轴对称的点的横坐标是 .
14.(2分)如图,一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是 .
15.(2分)△ABC的三个内角的度数之比是1:3:5,如果按角分类,那么△ABC是 三角形.
16.(2分)如图:已知AB=CD,使△ABO≌△CDO,还需添加一个条件,你添加的条件是 .(只需一个,不添加辅助线)
17.(2分)如图,在等腰△ABC中,AB=AC,点O是△ABC内一点,且OB=OC,联结AO并延长,交边BC于点D.如果BD=3,那么BC的值为 .
18.(2分)已知△ABC≌△A'B'C',等腰△ABC的周长为14cm,BC=6cm,那么△A'B'C'的底边长等于 .
19.(2分)如图,将直角三角形(∠ACB为直角)沿线段CD折叠使B落在B'处,若∠ACB'=50°,则∠ACD的度数为 .
20.(2分)如图是一组密码的一部分,为了保密,许多情况下采用不同的密码.请你运用所学知识,找到破译的“钥匙”.目前,据此“钥匙”已破译出“动脑思考”的真实意思是“装好收获”.请破译“正在做题”真实意思是 .
三、简答题:(本大题共5题,每题6分,满分30分)
21.(6分)计算:﹣12019+()﹣3+()2019?(﹣4)2019﹣(3﹣π)0.
22.(6分)利用幂的性质计算:(25×75)÷14(结果表示为幂的形式).
23.(6分)如图,已知∠A的两边与∠D的两边分别平行,且∠D比∠A的2倍多30°,求∠D的度数.
24.(6分)阅读并填空.已知:如图,线BCF、线AEF是直线,AB∥CD,∠1=∠2,∠3=∠4.试说明AD∥BC.
解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAE=∠2+∠CAE( )
即∠BAE=∠
∴∠3=∠ ( )
∴AD∥BC( )
25.(6分)如图,在直角坐标平面内,已知点A的坐标是(0,4),点B的坐标是(﹣2,﹣3)
(1)图中点C的坐标是 .
(2)点C关于x轴对称的点D的坐标是 .
(3)如果将点B沿着与x轴平行的方向向右平移2个单位得到点B',那么A、B'两点之间的距离是 .
(4)图中△ACD的面积是 .
四、解答题(本大题共3题,其中第26题7分,第27题8分,第28题9分,满分24分)
26.(7分)如图,两车从路段MN的两端同时出发,以相同的速度行驶,相同时间后分别到达A,B两地,两车行进的路线平行.那么A,B两地到路段MN的距离相等吗?为什么?
27.(8分)如图,已知AB=AD,∠ABC=∠ADC.试判断AC与BD的位置关系,并说明理由.
28.(9分)如图,在等腰△ABC中,AB=AC,点M是直线BC上一点(不与B、C重合).以AM为一边在AM的右侧作等腰△AMN,使∠MAN=∠BAC,AM=AN,联结CN.
(1)如图(1),当点M在线段BC上时,如果∠BAC=90°,∠BCN= °;
(2)设∠BAC=α,∠BCN=β,
①如图(2),当点M在线段BC上移动时,α、β之间有怎样的数量关系?请说明理由.
②当点M在直线BC上移动时,α、β之间有怎样的数量关系?请直接写出你的结论.
2019-2020学年上海市嘉定区七年级(下)期末数学试卷
参考答案与试题解析
一、选择题:(本大题共6题,每题3分,满分18分)
1.下列各数:3.14,﹣,,π,5.3,0.2020020002……(它的位数无限且相邻两个2之间“0”的个数依次加1个),其中无理数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据无理数的定义求解即可.
【解答】解:,π,0.2020020002……(它的位数无限且相邻两个2之间“0”的个数依次加1个)是无理数,共有3个,
故选:C.
2.下列各式中,正确的是( )
A.(﹣a)﹣2=a2 B.a?(﹣a)2=﹣a3
C.a3÷(﹣a)2=﹣a D.(﹣a3)2=a6
【分析】分别根据负整数指数幂的定义,同底数幂的乘法法则,同底数幂的除法法则以及幂的乘方运算法则逐一判断即可.
【解答】解:A.(﹣a)﹣2=,故本选项不符合题意;
B.a?(﹣a)2=a3,故本选项不符合题意;
C.a3÷(﹣a)2=a,故本选项不符合题意;
D.(﹣a3)2=a6,故本选项符合题意;
故选:D.
3.已知点A(m﹣1,m+4)在x轴上,则点A的坐标是( )
A.(0,5) B.(﹣5,0) C.(0,3) D.(﹣3,0)
【分析】直接利用x轴上点的坐标特点得出m的值,即可得出答案.
【解答】解:∵A(m﹣1,m+4)在x轴上,
∴m+4=0,
解得:m=﹣4,
∴m﹣1=﹣5,
∴点A的坐标是:(﹣5,0).
故选:B.
4.如图,将三角板的直角顶点放在直尺的一边上,如果∠1=70°,那么∠2的度数为( )
A.10° B.15° C.20° D.25°
【分析】利用平行线的性质可得∠3的度数,再利用平角定义可得∠2的度数.
【解答】解:∵a∥b,
∴∠1=∠3=70°,
∵∠4=90°,
∴∠2=180°﹣90°﹣70°=20°,
故选:C.
5.下列说法中,正确的是( )
A.腰对应相等的两个等腰三角形全等
B.等腰三角形角平分线与中线重合
C.底边和顶角分别对应相等的两个等腰三角形全等
D.形状相同的两个三角形全等
【分析】根据全等三角形的判定判断即可.
【解答】解:A、腰对应相等的两个等腰三角形不一定全等,因为角不一定相等,选项错误,不符合题意;
B、等腰三角形顶角的角平分线与底边的中线重合,选项错误,不符合题意;
C、底边和顶角分别对应相等的两个等腰三角形全等,利用ASA可得全等,选项正确,符合题意;
D、形状、大小相同的两个三角形全等,选项错误,不符合题意;
故选:C.
6.现有1cm、3cm、5cm、6cm长的四根木棒,任选其中三根组成一个三角形,那么可以组成三角形的个数是( )
A.1 B.2 C.3 D.4
【分析】从4条线段里任取3条线段组合,可有4种情况,看哪种情况不符合三角形三边关系,舍去即可.
【解答】解:四条木棒的所有组合:1,3,5和1,3,6和1,5,6和3,5,6;
只有3,5,6能组成三角形.
故选:A.
二、填空题:(本大题共14题,每题2分,满分28分)
7.(2分)实数36的算术平方根是 6 .
【分析】根据算术平方根的定义即可作答.
【解答】解:∵62=36,
∴36的算术平方根是6.
8.(2分)把表示成幂的形式是 .
【分析】根据分数指数幂即可求出答案.
【解答】解:.
故答案为:.
9.(2分)计算:()4+= 6 .
【分析】直接利用二次根式的性质进而分别计算得出答案.
【解答】解:原式=4+2
=6.
故答案为:6.
10.(2分)比较大小:﹣ < ﹣3(填“>”、“<”、“=”).
【分析】先把3化成,再与进行比较,即可得出结果.
【解答】解:∵3=,
∴>,
∴>3,
∴﹣<﹣3,
故答案为:<.
11.(2分)近似数1.2567×105有 5 个有效数字.
【分析】科学记数法的一般形式为a×10n,其中,1≤|a|<10,n为整数数位减1,有效数字应是a×10n中a的有效数字,即乘号前面的所有数字.
【解答】解:1.2567×105有1、2、5、6、7共5个有效数字;
故答案为5.
12.(2分)人体中成熟的红细胞平均直径为0.00077厘米,将数字0.00077用科学记数法表示为 7.7×10﹣4 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.00077=7.7×10﹣4.
故答案为:7.7×10﹣4.
13.(2分)与点P(﹣2,3)关于x轴对称的点的横坐标是 ﹣2 .
【分析】直接利用关于x轴对称点的性质,横坐标不变,纵坐标互为相反数,进而得出答案.
【解答】解:点P(﹣2,3)关于x轴对称的点的横坐标是﹣2.
故答案为:﹣2.
14.(2分)如图,一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是 105° .
【分析】先根据AD∥BC求出∠3的度数,再根据AB∥CD即可得出结论.
【解答】解:如图,∵AD∥BC,∠1=75°,
∴∠3=∠1=75°,
∵AB∥CD,
∴∠2=180°﹣∠3=180°﹣75°=105°.
故答案为:105°.
15.(2分)△ABC的三个内角的度数之比是1:3:5,如果按角分类,那么△ABC是 钝角 三角形.
【分析】已知三角形三个内角的度数之比,可以设一份为k°,根据三角形的内角和等于180°列方程求三个内角的度数,从而确定三角形的形状.
【解答】解:设一份为k°,则三个内角的度数分别为k°,3k°,5k°.
则k°+3k°+5k°=180°,
解得k=20,
∴5k°=100°,
所以这个三角形是钝角三角形.
故答案为:钝角.
16.(2分)如图:已知AB=CD,使△ABO≌△CDO,还需添加一个条件,你添加的条件是 ∠A=∠C .(只需一个,不添加辅助线)
【分析】由图形可知∠AOB=∠COD,结合条件,根据全等三角形的判定方法填写答案即可.
【解答】解:
∵AB=CD,且∠AOB=∠COD,
∴当∠B=∠D或∠A=∠C时,满足AAS,可证明△ABO≌△CDO,
故答案为:∠A=∠C(∠B=∠D).
17.(2分)如图,在等腰△ABC中,AB=AC,点O是△ABC内一点,且OB=OC,联结AO并延长,交边BC于点D.如果BD=3,那么BC的值为 6 .
【分析】证△ABO≌△ACO(SAS),得出∠BAO=∠CAO,由等腰三角形的性质得出CD=BD=3,即可得出答案.
【解答】解:∵AB=AC,OB=OC,
∴∠ABC=∠ACB,∠OBC=∠OCB,
∴∠ABO=∠ACO,
在△ABO和△ACO中,,
∴△ABO≌△ACO(SAS),
∴∠BAO=∠CAO,
∵AB=AC
∴CD=BD=3,
∴BC=2BD=6;
故答案为:6.
18.(2分)已知△ABC≌△A'B'C',等腰△ABC的周长为14cm,BC=6cm,那么△A'B'C'的底边长等于 4cm或2cm .
【分析】根据全等三角形的性质得出AB=A′B′,BC=B′C′,AC=A′C′,分为两种情况,求出即可.
【解答】解:∵△ABC≌△A′B′C′,
∴AB=A′B′,BC=B′C′,AC=A′C′,
分为两种情况:
①当BC是底边时,腰AB=AC,A′B′=A′C′,
∵△ABC≌△A′B′C′,
∴AB=AC=A′B′=A′C′,
∵等腰△ABC的周长为14cm,BC=6cm,
∴△A′B′C′中一定有一条底边B′C′的长是4cm,
②BC是腰时,腰是6cm,
∵等腰△ABC的周长为14cm,
∴△A′B′C′中一定有一条底边的长是14﹣6﹣6=2(cm),
即底边长是4cm或2cm,
故答案为:4cm或2cm.
19.(2分)如图,将直角三角形(∠ACB为直角)沿线段CD折叠使B落在B'处,若∠ACB'=50°,则∠ACD的度数为 20° .
【分析】根据翻折的性质可知:∠BCD=∠B′CD,又∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+60°=150°,继而即可求出∠BCD的值,又∠ACD+∠BCD=∠ACB=90°,继而即可求出∠ACD的度数.
【解答】解:∵△B′CD是由△BCD翻折得到的,
∴∠BCD=∠B′CD,
又∵∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+50°=140°,
∴∠BCD=70°,
又∵∠ACD+∠BCD=∠ACB=90°,
∴∠ACD=20°.
故答案为:20°.
20.(2分)如图是一组密码的一部分,为了保密,许多情况下采用不同的密码.请你运用所学知识,找到破译的“钥匙”.目前,据此“钥匙”已破译出“动脑思考”的真实意思是“装好收获”.请破译“正在做题”真实意思是 “我爱数学” .
【分析】根据题意可以发现对应字之间的规律,从而可以解答本题.
【解答】解:由题意可得,
“动脑思考”的真实意思是“装好收获”.“动”所对应的字为“装”,是“动”字先向右平移一个单位,再向上平移两个得到的“装”,其他各个字对应也是这样得到的,
∴“正在做题”的真实意思是“我爱数学”,
故答案为:“我爱数学”.
三、简答题:(本大题共5题,每题6分,满分30分)
21.(6分)计算:﹣12019+()﹣3+()2019?(﹣4)2019﹣(3﹣π)0.
【分析】根据根据有理数的乘方的定义,负整数指数幂的定义,积的乘方运算法则以及任何非零数的零次幂等于1计算即可.
【解答】解:原式=﹣1+
=﹣1+8﹣12019﹣1
=﹣1+8﹣1﹣1
=5.
22.(6分)利用幂的性质计算:(25×75)÷14(结果表示为幂的形式).
【分析】先根据积的乘方运算法则化简,再根据幂的乘方运算法则以及同底数幂的除法法则计算即可.
【解答】解:(25×75)÷14
=
=
=
=.
23.(6分)如图,已知∠A的两边与∠D的两边分别平行,且∠D比∠A的2倍多30°,求∠D的度数.
【分析】利用平行线的性质可得出∠A+∠D=180°,结合∠D比∠A的2倍多30°,即可求出∠D的度数.
【解答】解:∵AB∥DE,
∴∠1=∠A,
∵AC∥DF,
∴∠1+∠D=180°,
∴∠A+∠D=180°①,
∵∠D=2∠A+30°②,
解①②组成的方程组得∠D=130°.
24.(6分)阅读并填空.已知:如图,线BCF、线AEF是直线,AB∥CD,∠1=∠2,∠3=∠4.试说明AD∥BC.
解:∵AB∥CD(已知)
∴∠4=∠ BAE ( 两直线平行,同位角相等 )
∵∠3=∠4(已知)
∴∠3=∠ BAE ( 等量代换 )
∵∠1=∠2(已知)
∴∠1+∠CAE=∠2+∠CAE( 等式的性质 )
即∠BAE=∠ DAC
∴∠3=∠ DAC ( 等量代换 )
∴AD∥BC( 同错角相等,两直线平行 )
【分析】由AB∥CD得∠4=∠BAE,根据等量代换,等式的性质得∠3=∠DAC,最后由内错角相等,两直平行判定直线AD∥BC.
【解答】解:如图所示:
∵AB∥CD,
∴∠4=∠BAE(两直线平行,同位角相等),
又∵∠3=∠4,
∴∠3=∠BAE(等量代换),
又∵∠1=∠2,
∴∠1+∠CAE=∠2+∠CAE(角的和差),
∴∠BAE=∠DAC,
∴∠3=∠DAC(等量代换),
∴AD∥BC(内错角相等,两直线平行),
故答案为:BAE,两直线平行,同位角相等;BAE,等量代换,
等式的性质,DAC,DAC,等量代换,同错角相等,两直线平行.
25.(6分)如图,在直角坐标平面内,已知点A的坐标是(0,4),点B的坐标是(﹣2,﹣3)
(1)图中点C的坐标是 (2,﹣3) .
(2)点C关于x轴对称的点D的坐标是 (2,3) .
(3)如果将点B沿着与x轴平行的方向向右平移2个单位得到点B',那么A、B'两点之间的距离是 7 .
(4)图中△ACD的面积是 6 .
【分析】(1)根据平面直角坐标系可直接写出C点坐标;
(2)根据关于x轴对称的点的坐标特点:横坐标不变,纵坐标互为相反数可得D点坐标;
(3)根据点的平移:横坐标,右移加,左移减;纵坐标,上移加,下移减可得B′点坐标,进而得到答案;
(4)根据三角形的面积公式可得答案.
【解答】解:(1)图中点C的坐标是(2,﹣3).
(2)点C关于x轴对称的点D的坐标是(2,3).
(3)如果将点B沿着与x轴平行的方向向右平移2个单位得到点B'(﹣2+2,﹣3),即(0,﹣3),那么A、B'两点之间的距离是:4﹣(﹣3)=7.
(4)图中△ACD的面积:=.
故答案为:(1)(2,﹣3);(2)(2,3);(3)7;(4)6.
四、解答题(本大题共3题,其中第26题7分,第27题8分,第28题9分,满分24分)
26.(7分)如图,两车从路段MN的两端同时出发,以相同的速度行驶,相同时间后分别到达A,B两地,两车行进的路线平行.那么A,B两地到路段MN的距离相等吗?为什么?
【分析】要判断A,B两地到路段MN的距离是否相等,可以由条件证明△AEM≌△BFN,再根据全等三角形的性质就可以的得出结论.
【解答】解:A,B两地到路段MN的距离相等.
理由:∵AE⊥MN,BF⊥MN,
∴∠AFN=∠AEM=90°.
∵AM∥BN,
∴∠M=∠N.
在△AEM和△BFN中,
,
∴△AEM≌△BFN(AAS),
∴AE=BF.
∴A,B两地到路段MN的距离相等.
27.(8分)如图,已知AB=AD,∠ABC=∠ADC.试判断AC与BD的位置关系,并说明理由.
【分析】AC与BD垂直,理由为:由AB=AD,利用等边对等角得到一对角相等,利用等式性质得到∠BDC=∠DBC,利用等角对等边得到DC=BC,利用SSS得到三角形ABC与三角形ADC全等,利用全等三角形对应角相等得到∠DAC=∠BAC,再利用三线合一即可得证.
【解答】解:AC⊥BD,理由为:
∵AB=AD(已知),
∴∠ADB=∠ABD(等边对等角),
∵∠ABC=∠ADC(已知),
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB(等式性质),即∠BDC=∠DBC,
∴DC=BC(等角对等边),
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠DAC=∠BAC(全等三角形的对应角相等),
又∵AB=AD,
∴AC⊥BD(等腰三角形三线合一).
28.(9分)如图,在等腰△ABC中,AB=AC,点M是直线BC上一点(不与B、C重合).以AM为一边在AM的右侧作等腰△AMN,使∠MAN=∠BAC,AM=AN,联结CN.
(1)如图(1),当点M在线段BC上时,如果∠BAC=90°,∠BCN= 90 °;
(2)设∠BAC=α,∠BCN=β,
①如图(2),当点M在线段BC上移动时,α、β之间有怎样的数量关系?请说明理由.
②当点M在直线BC上移动时,α、β之间有怎样的数量关系?请直接写出你的结论.
【分析】(1)由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAM≌△CAN,可得∠ABC=∠ACN=45°,可求∠BCN的度数;
(2)①由“SAS”可证△ABM≌△ACN得出∠ABM=∠ACN,再用三角形的内角和即可得出结论;
②分两种情况画出图形,由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和与外角的性质即可得出结论.
【解答】解:(1)∵AB=AC,∠BAC=90°,
则∠ABC=∠ACB=45°,
∵∠MAN=∠BAC,
∴∠BAM=∠CAN,且AB=AC,AM=AN,
∴△BAM≌△CAN(SAS),
∴∠ABC=∠ACN=45°,
∴∠BCN=∠ACB+∠ACN=90°,
故答案为:90;
(2)①α+β=180°,理由如下:
∵∠BAC=∠MAN,
∴∠BAC﹣∠MAC=∠MAN﹣∠MAC.
即∠BAM=∠CAN.
在△ABM与△ACN中,
,
∴△ABM≌△ACN(SAS),
∴∠B=∠ACN.
∴∠B+∠ACB=∠ACN+∠ACB.
∵∠ACN+∠ACB=β,
∴∠B+∠ACB=β,
∵α+∠B+∠ACB=180°,
∴α+β=180°;
②当点M在BC的延长线上时,α+β=180°,如图:
理由如下:∵∠BAC=∠MAN,
∴∠BAM=∠CAN,
在△ABD和△ACE中,
,
∴△ABM≌△ACN(SAS),
∴∠ABM=∠ACN,
在△ABC中,∠BAC+∠ABM+∠ACB=180°,
∴∠BAC+∠ACN+∠ACB=∠BAC+∠BCN=180°,
即:α+β=180°.
当点M在CB的延长线上时,α=β,如图:
理由如下:∵∠BAC=∠MAN,
∴∠BAM=∠CAN,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(SAS),
∴∠ABM=∠ACN,
∵∠ABM=∠α+∠ACB,∠ACN=∠β+∠ACB,
∴α=β.
综上,α+β=180°或α=β.
同课章节目录
