人教版七年级上册数学习题课件 第2章 集训课堂 测素质 认识整式(30张PPT)
文档属性
| 名称 | 人教版七年级上册数学习题课件 第2章 集训课堂 测素质 认识整式(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 373.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 00:00:00 | ||
图片预览








文档简介
测素质
课题2
人教版 七年级上
第二章 整式的加减
集训课堂
认识整式
D
A
1
2
3
4
5
D
A
6
7
8
10
D
C
B
11
12
答 案 呈 现
温馨提示:点击 进入讲评
9
C
习题链接
(3a+4b)
1;2
3a
-3
13
14
15
16
17
18
温馨提示:点击 进入讲评
习题链接
19
D
1
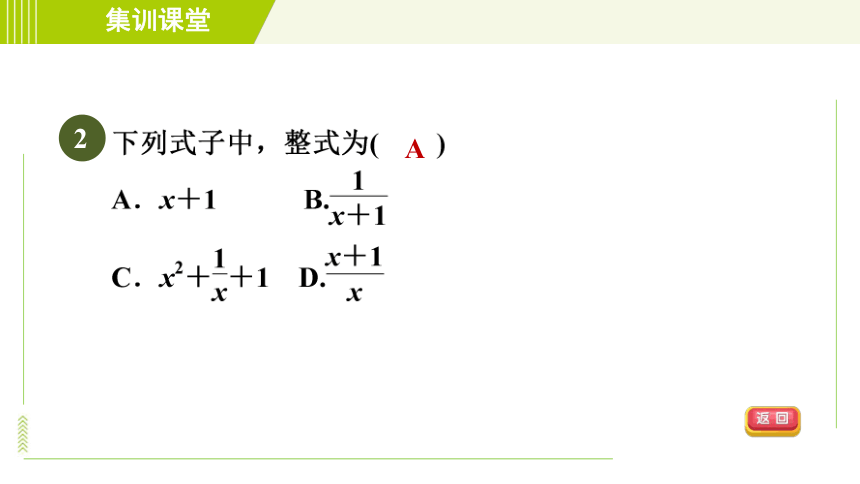
2
A
我们知道,用字母表示的式子是具有一般意义的,请仔细分析下列赋予3a实际意义的例子中不正确的是( )
A.若葡萄的价格是3元/千克,则3a表示买a千克葡萄的金额
B.若a表示一个等边三角形的边长,则3a表示这个等边三角形的周长
C.若a表示某正方形的面积,则3a表示3个这样的正方形的面积
D.若3和a分别表示一个两位数中的十位数字和个位数字,则3a表示这个两位数
3
D
A
4
当x=1,y=-2时,整式2x+y-1的值是( )
A.1 B.-2 C.2 D.-1
D
5
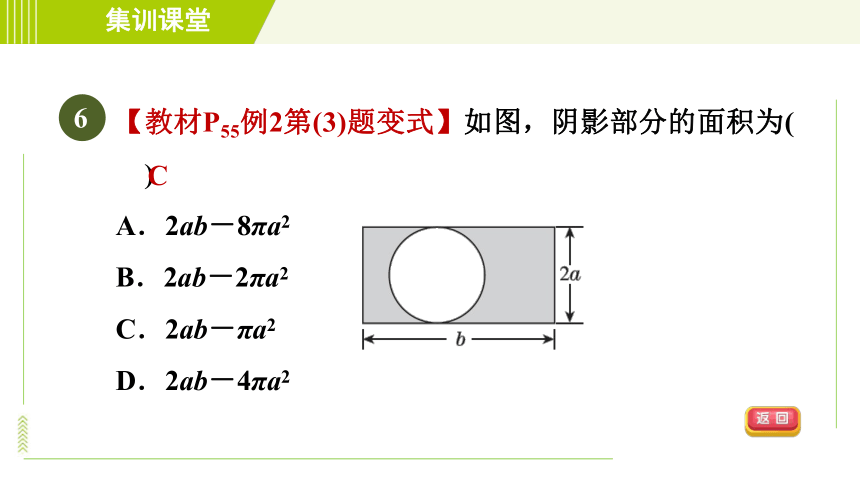
【教材P55例2第(3)题变式】如图,阴影部分的面积为( )
A.2ab-8πa2
B.2ab-2πa2
C.2ab-πa2
D.2ab-4πa2
6
C
某品牌液晶电视机原价为m元,由于技术更新,成本降低,现降价30%,则该品牌电视机现价为( )
A.(m-30%)元 B.30%m元
C.(1-30%)m元 D.(1+30%)m元
C
7
8.观察下列单项式:-2x,22x2,-23x3,24x4,…,-219x19,220x20,…,则第n个单项式是( )
A.2nxn B.(-1)n2nxn
C.-2nxn D.(-1)n+12nxn
B
8
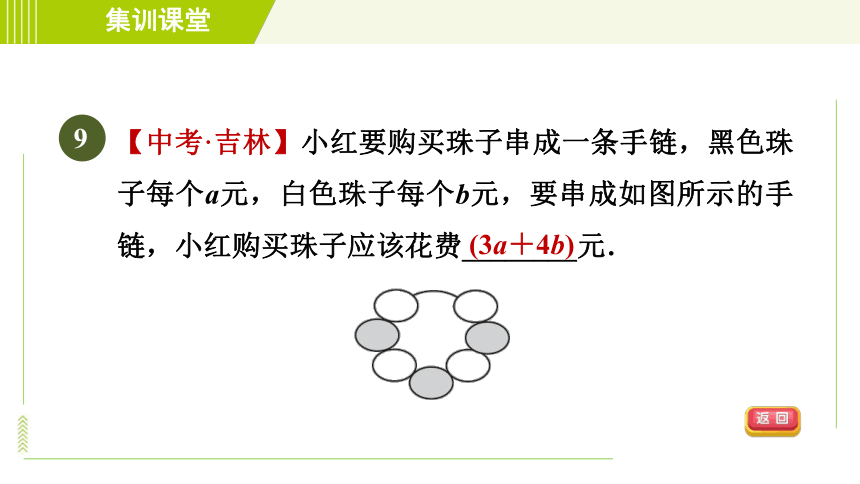
【中考·吉林】小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费________元.
(3a+4b)
9
如果单项式(5m-2)x2yn+1是关于x,y的系数为3的五次单项式,则m=________,n=________.
1
10
2
在如图的月历中,任意圈出一竖列相邻的三个数,设中间的一个数为a,则这三个数之和为______.(用含a的式子表示)
3a
11
若关于x的多项式6x2-7x+2mx2+3不含x的二次项,则m=________.
12
-3
-6或-24
13
如图,观察下列图形,可得它们是按一定规律排列的.依照此规律,解决下列问题.
14
(1)第5个图形有________颗五角星,第6个图形有________颗五角星;
(2)第2 020个图形有________颗五角星,第n个图形有________颗五角星.
16
19
6 061
(3n+1)
15
(1)单项式:_______________________________;
(2)多项式:_______________________________;
(3)整式:_________________________________.
③④⑨
①②⑤
①②③④⑤⑨
(8分)已知关于y的多项式(a-4)y3-2yb+y-ab为二次三项式.
(1)求a,b的值;
解:因为关于y的多项式(a-4)y3-2yb+y-ab为二次三项式,所以a-4=0,b=2,即a=4,b=2.
16
(2)当y=-3时,求这个二次三项式的值.
解:把a=4,b=2代入关于y的多项式得-2y2+y-8.
当y=-3时,-2y2+y-8=-2×(-3)2+(-3)-8=-29.
(10分)【教材P70习题T7改编】如图是一个工件的横截面及其尺寸(单位:cm).
17
(1)用含a,b的式子表示它的面积S;
(2)当a=15,b=8时,求S的值.(π取3.14,精确到0.01 cm2)
(10分)定义:f(a,b)是关于a,b的多项式,如果f(a,b)=f(b,a),那么f(a,b)叫做“对称多项式”.例如:若f(a,b)=a2+a+b+b2,则f(b,a)=b2+b+a+a2,所以f(a,b)=f(b,a),所以f(a,b)是“对称多项式”.
18
(1)试说明f(a,b)=a2-2ab+b2是“对称多项式”;
(2)请写出一个“对称多项式”,f(a,b)=_______________;(不多于四项)
解:因为f(a,b)=a2-2ab+b2,所以f(b,a)=b2-2ba+a2,所以f(a,b)=f(b,a),故f(a,b)=a2-2ab+b2是“对称多项式”.
a+b(答案不唯一)
(3)如果f1(a,b)和f2(a,b)均为“对称多项式”,那么f1(a,b)+f2(a,b)一定是“对称多项式”吗?如果一定是,请说明理由;如果不一定是,请举例说明.
解:不一定是.举例:f1(a,b)=a+b,f2(a,b)=-a-b,f1(a,b),f2(a,b)都是“对称多项式”,而f1(a,b)+f2(a,b)=0,是单项式,不是多项式(所举例子不唯一).
19
(10分)学校餐厅中,一张桌子可坐6人,有以下两种摆放方式(如图):
(1)当有5张桌子时,两种摆放方式各能坐多少人?
(2)当有n张桌子时,两种摆放方式各能坐多少人?(用含n的式子表示)
解:用第一种摆放方式可以坐5×4+2=22(人);
用第二种摆放方式可以坐5×2+4=14(人).
用第一种摆放方式可以坐(4n+2)人;
用第二种摆放方式可以坐(2n+4)人.
解:选择第一种方式.理由如下:
第一种方式:60张桌子一共可以坐60×4+2=242(人);
第二种方式:60张桌子一共可以坐60×2+4=124(人).
因为242>200>124,所以选择第一种方式.
(3)新学期将有200人在学校就餐,但餐厅只有60张这样的桌子,若你是老师,你打算选择哪种方式来摆放桌子?为什么?
课题2
人教版 七年级上
第二章 整式的加减
集训课堂
认识整式
D
A
1
2
3
4
5
D
A
6
7
8
10
D
C
B
11
12
答 案 呈 现
温馨提示:点击 进入讲评
9
C
习题链接
(3a+4b)
1;2
3a
-3
13
14
15
16
17
18
温馨提示:点击 进入讲评
习题链接
19
D
1
2
A
我们知道,用字母表示的式子是具有一般意义的,请仔细分析下列赋予3a实际意义的例子中不正确的是( )
A.若葡萄的价格是3元/千克,则3a表示买a千克葡萄的金额
B.若a表示一个等边三角形的边长,则3a表示这个等边三角形的周长
C.若a表示某正方形的面积,则3a表示3个这样的正方形的面积
D.若3和a分别表示一个两位数中的十位数字和个位数字,则3a表示这个两位数
3
D
A
4
当x=1,y=-2时,整式2x+y-1的值是( )
A.1 B.-2 C.2 D.-1
D
5
【教材P55例2第(3)题变式】如图,阴影部分的面积为( )
A.2ab-8πa2
B.2ab-2πa2
C.2ab-πa2
D.2ab-4πa2
6
C
某品牌液晶电视机原价为m元,由于技术更新,成本降低,现降价30%,则该品牌电视机现价为( )
A.(m-30%)元 B.30%m元
C.(1-30%)m元 D.(1+30%)m元
C
7
8.观察下列单项式:-2x,22x2,-23x3,24x4,…,-219x19,220x20,…,则第n个单项式是( )
A.2nxn B.(-1)n2nxn
C.-2nxn D.(-1)n+12nxn
B
8
【中考·吉林】小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费________元.
(3a+4b)
9
如果单项式(5m-2)x2yn+1是关于x,y的系数为3的五次单项式,则m=________,n=________.
1
10
2
在如图的月历中,任意圈出一竖列相邻的三个数,设中间的一个数为a,则这三个数之和为______.(用含a的式子表示)
3a
11
若关于x的多项式6x2-7x+2mx2+3不含x的二次项,则m=________.
12
-3
-6或-24
13
如图,观察下列图形,可得它们是按一定规律排列的.依照此规律,解决下列问题.
14
(1)第5个图形有________颗五角星,第6个图形有________颗五角星;
(2)第2 020个图形有________颗五角星,第n个图形有________颗五角星.
16
19
6 061
(3n+1)
15
(1)单项式:_______________________________;
(2)多项式:_______________________________;
(3)整式:_________________________________.
③④⑨
①②⑤
①②③④⑤⑨
(8分)已知关于y的多项式(a-4)y3-2yb+y-ab为二次三项式.
(1)求a,b的值;
解:因为关于y的多项式(a-4)y3-2yb+y-ab为二次三项式,所以a-4=0,b=2,即a=4,b=2.
16
(2)当y=-3时,求这个二次三项式的值.
解:把a=4,b=2代入关于y的多项式得-2y2+y-8.
当y=-3时,-2y2+y-8=-2×(-3)2+(-3)-8=-29.
(10分)【教材P70习题T7改编】如图是一个工件的横截面及其尺寸(单位:cm).
17
(1)用含a,b的式子表示它的面积S;
(2)当a=15,b=8时,求S的值.(π取3.14,精确到0.01 cm2)
(10分)定义:f(a,b)是关于a,b的多项式,如果f(a,b)=f(b,a),那么f(a,b)叫做“对称多项式”.例如:若f(a,b)=a2+a+b+b2,则f(b,a)=b2+b+a+a2,所以f(a,b)=f(b,a),所以f(a,b)是“对称多项式”.
18
(1)试说明f(a,b)=a2-2ab+b2是“对称多项式”;
(2)请写出一个“对称多项式”,f(a,b)=_______________;(不多于四项)
解:因为f(a,b)=a2-2ab+b2,所以f(b,a)=b2-2ba+a2,所以f(a,b)=f(b,a),故f(a,b)=a2-2ab+b2是“对称多项式”.
a+b(答案不唯一)
(3)如果f1(a,b)和f2(a,b)均为“对称多项式”,那么f1(a,b)+f2(a,b)一定是“对称多项式”吗?如果一定是,请说明理由;如果不一定是,请举例说明.
解:不一定是.举例:f1(a,b)=a+b,f2(a,b)=-a-b,f1(a,b),f2(a,b)都是“对称多项式”,而f1(a,b)+f2(a,b)=0,是单项式,不是多项式(所举例子不唯一).
19
(10分)学校餐厅中,一张桌子可坐6人,有以下两种摆放方式(如图):
(1)当有5张桌子时,两种摆放方式各能坐多少人?
(2)当有n张桌子时,两种摆放方式各能坐多少人?(用含n的式子表示)
解:用第一种摆放方式可以坐5×4+2=22(人);
用第二种摆放方式可以坐5×2+4=14(人).
用第一种摆放方式可以坐(4n+2)人;
用第二种摆放方式可以坐(2n+4)人.
解:选择第一种方式.理由如下:
第一种方式:60张桌子一共可以坐60×4+2=242(人);
第二种方式:60张桌子一共可以坐60×2+4=124(人).
因为242>200>124,所以选择第一种方式.
(3)新学期将有200人在学校就餐,但餐厅只有60张这样的桌子,若你是老师,你打算选择哪种方式来摆放桌子?为什么?
