人教版七年级上册数学习题课件 第2章 集训课堂 练素养 整式化简求值的常见题型(20张PPT)
文档属性
| 名称 | 人教版七年级上册数学习题课件 第2章 集训课堂 练素养 整式化简求值的常见题型(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 268.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 22:32:42 | ||
图片预览







文档简介
练素养
课题2
人教版 七年级上
第二章 整式的加减
集训课堂
整式化简求值的常见题型
1
2
3
4
5
6
7
8
10
11
温馨提示:点击 进入讲评
9
习题链接
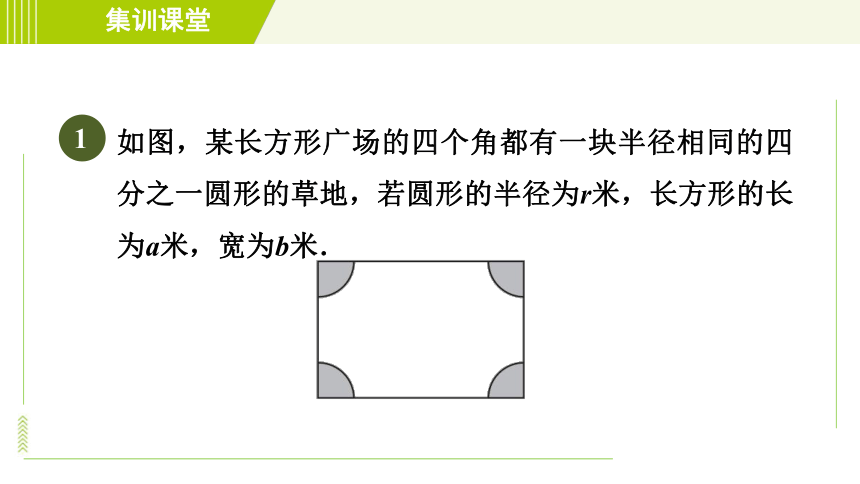
如图,某长方形广场的四个角都有一块半径相同的四分之一圆形的草地,若圆形的半径为r米,长方形的长为a米,宽为b米.
1
(1)分别用整式表示草地和空地的面积;
(2)若长方形的长为300米,宽为200米,圆形的半径为10米,求广场空地的面积(结果精确到个位).
当a=300,b=200,r=10时,ab-πr2=300×200-100π≈59 686.
故广场空地的面积约为59 686平方米.
2
解:因为a,b互为相反数,c,d互为倒数,|x|=1,
所以a+b=0,cd=1,x=±1,
当a+b=0,cd=1,x=1时,原式=0+12-1×1=0+1-1=0;当a+b=0,cd=1,x=-1时,
原式=0+(-1)2-1×(-1)=1-(-1)=2.
综上所述,式子a+b+x2-cdx的值为0或2.
已知a,b互为相反数,c,d互为倒数,|x|=1,求式子a+b+x2-cdx的值.
已知A=3a2-6ab+b2,B=-a2-5ab-7b2,
其中a=-1,b=1,求-3A+2B的值.
3
解:-3A+2B
=-3(3a2-6ab+b2)+2(-a2-5ab-7b2)
=-9a2+18ab-3b2-2a2-10ab-14b2
=(-9-2)a2+(18-10)ab+(-3-14)b2
=-11a2+8ab-17b2.
当a=-1,b=1时,
-11a2+8ab-17b2
=-11×(-1)2+8×(-1)×1-17×12
=-11×1+8×(-1)-17×1
=-11+(-8)-17
=-36.
所以-3A+2B的值为-36.
解:由题意,得m+1+1=6,7-m+3n=6,解得m=4,n=1,所以m2+n2=42+12=17.
4
(2)若a=-1,b=-2,求该多项式的值.
5
已知A+B=3x2-5x+1,A-C=-2x+3x2-5,求当x=2时B+C的值.[提示:B+C=(A+B)-(A-C)]
6
解:B+C=(A+B)-(A-C)=3x2-5x+1-(-2x+3x2-5)=3x2-5x+1+2x-3x2+5
=(3-3)x2+(-5+2)x+1+5=-3x+6.
当x=2时,-3x+6=-3×2+6=-6+6=0.
所以当x=2时,B+C的值为0.
已知a2-a-4=0,求4a2-2(a2-a+3)-(a2-a-4)-4a的值.
解:原式=4a2-2a2+2a-6-a2+a+4-4a=a2-a-2.又因为a2-a-4=0,所以a2-a=4,
所以原式=4-2=2.
7
8
已知(2x+3)4=a0x4+a1x3+a2x2+a3x+a4,求下列各式的值;
(1)a0+a1+a2+a3+a4;
解:将x=1代入(2x+3)4=a0x4+a1x3+a2x2+a3x+a4,
得a0+a1+a2+a3+a4=(2+3)4=625.
9
(2)a0-a1+a2-a3+a4;
解:将x=-1代入(2x+3)4=
a0x4+a1x3+a2x2+a3x+a4,
得a0-a1+a2-a3+a4=(-2+3)4=1.
(3)a0+a2+a4.
解:因为(a0+a1+a2+a3+a4)+(a0-a1+a2-a3+a4)=2(a0+a2+a4),
所以625+1=2(a0+a2+a4),所以a0+a2+a4=313.
【点拨】
本题中直接求各项系数所组成式子的值是行不通的,观察各式的特点可以发现,通过赋予x特殊值可以求出式子的值.
解:(2x2+ax-y+6)-(2bx2-3x+5y-1)
=2x2+ax-y+6-2bx2+3x-5y+1
=(2-2b)x2+(a+3)x-6y+7.
因为上式的值与字母x所取的值无关,
所以2-2b=0,a+3=0,即a=-3,b=1.
10
已知三个有理数a,b,c在数轴上的位置如图所示,且|a|=2,|b|=3,|c|=1.求a-b+c的值.
解:由题意及数轴可知a=-2,b=-3,c=1.
则a-b+c=-2-(-3)+1
=-2+3+1=1+1=2.
所以a-b+c的值为2.
11
课题2
人教版 七年级上
第二章 整式的加减
集训课堂
整式化简求值的常见题型
1
2
3
4
5
6
7
8
10
11
温馨提示:点击 进入讲评
9
习题链接
如图,某长方形广场的四个角都有一块半径相同的四分之一圆形的草地,若圆形的半径为r米,长方形的长为a米,宽为b米.
1
(1)分别用整式表示草地和空地的面积;
(2)若长方形的长为300米,宽为200米,圆形的半径为10米,求广场空地的面积(结果精确到个位).
当a=300,b=200,r=10时,ab-πr2=300×200-100π≈59 686.
故广场空地的面积约为59 686平方米.
2
解:因为a,b互为相反数,c,d互为倒数,|x|=1,
所以a+b=0,cd=1,x=±1,
当a+b=0,cd=1,x=1时,原式=0+12-1×1=0+1-1=0;当a+b=0,cd=1,x=-1时,
原式=0+(-1)2-1×(-1)=1-(-1)=2.
综上所述,式子a+b+x2-cdx的值为0或2.
已知a,b互为相反数,c,d互为倒数,|x|=1,求式子a+b+x2-cdx的值.
已知A=3a2-6ab+b2,B=-a2-5ab-7b2,
其中a=-1,b=1,求-3A+2B的值.
3
解:-3A+2B
=-3(3a2-6ab+b2)+2(-a2-5ab-7b2)
=-9a2+18ab-3b2-2a2-10ab-14b2
=(-9-2)a2+(18-10)ab+(-3-14)b2
=-11a2+8ab-17b2.
当a=-1,b=1时,
-11a2+8ab-17b2
=-11×(-1)2+8×(-1)×1-17×12
=-11×1+8×(-1)-17×1
=-11+(-8)-17
=-36.
所以-3A+2B的值为-36.
解:由题意,得m+1+1=6,7-m+3n=6,解得m=4,n=1,所以m2+n2=42+12=17.
4
(2)若a=-1,b=-2,求该多项式的值.
5
已知A+B=3x2-5x+1,A-C=-2x+3x2-5,求当x=2时B+C的值.[提示:B+C=(A+B)-(A-C)]
6
解:B+C=(A+B)-(A-C)=3x2-5x+1-(-2x+3x2-5)=3x2-5x+1+2x-3x2+5
=(3-3)x2+(-5+2)x+1+5=-3x+6.
当x=2时,-3x+6=-3×2+6=-6+6=0.
所以当x=2时,B+C的值为0.
已知a2-a-4=0,求4a2-2(a2-a+3)-(a2-a-4)-4a的值.
解:原式=4a2-2a2+2a-6-a2+a+4-4a=a2-a-2.又因为a2-a-4=0,所以a2-a=4,
所以原式=4-2=2.
7
8
已知(2x+3)4=a0x4+a1x3+a2x2+a3x+a4,求下列各式的值;
(1)a0+a1+a2+a3+a4;
解:将x=1代入(2x+3)4=a0x4+a1x3+a2x2+a3x+a4,
得a0+a1+a2+a3+a4=(2+3)4=625.
9
(2)a0-a1+a2-a3+a4;
解:将x=-1代入(2x+3)4=
a0x4+a1x3+a2x2+a3x+a4,
得a0-a1+a2-a3+a4=(-2+3)4=1.
(3)a0+a2+a4.
解:因为(a0+a1+a2+a3+a4)+(a0-a1+a2-a3+a4)=2(a0+a2+a4),
所以625+1=2(a0+a2+a4),所以a0+a2+a4=313.
【点拨】
本题中直接求各项系数所组成式子的值是行不通的,观察各式的特点可以发现,通过赋予x特殊值可以求出式子的值.
解:(2x2+ax-y+6)-(2bx2-3x+5y-1)
=2x2+ax-y+6-2bx2+3x-5y+1
=(2-2b)x2+(a+3)x-6y+7.
因为上式的值与字母x所取的值无关,
所以2-2b=0,a+3=0,即a=-3,b=1.
10
已知三个有理数a,b,c在数轴上的位置如图所示,且|a|=2,|b|=3,|c|=1.求a-b+c的值.
解:由题意及数轴可知a=-2,b=-3,c=1.
则a-b+c=-2-(-3)+1
=-2+3+1=1+1=2.
所以a-b+c的值为2.
11
