菱形的性质
图片预览






文档简介
(共32张PPT)
人教版数学教材八年级下
19.2特殊的平行四边形
19.2.2菱形的性质
观 察
下面的图形中有你熟悉的吗?
三菱汽车标志欣赏
读一读
越王勾践剑,一把在地下埋藏了2000多年的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列的黑色菱形暗花纹。
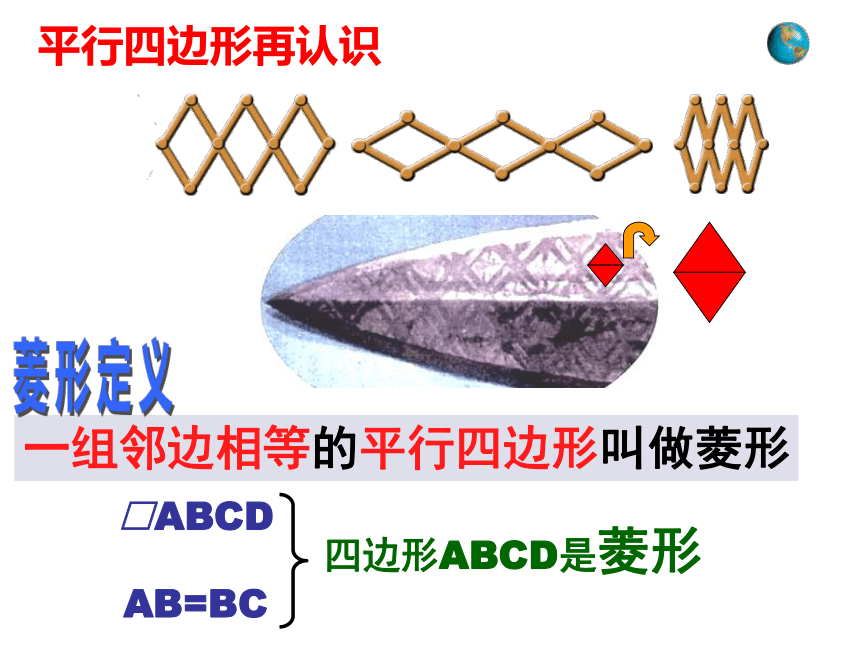
平行四边形再认识
一组邻边相等的平行四边形叫做菱形
AB=BC
四边形ABCD是菱形
□ABCD
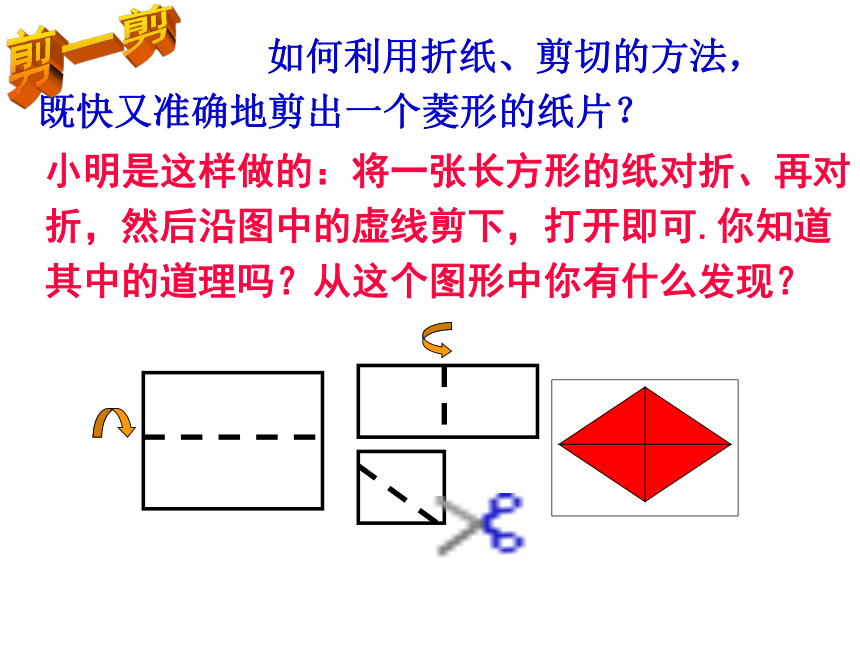
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?从这个图形中你有什么发现?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
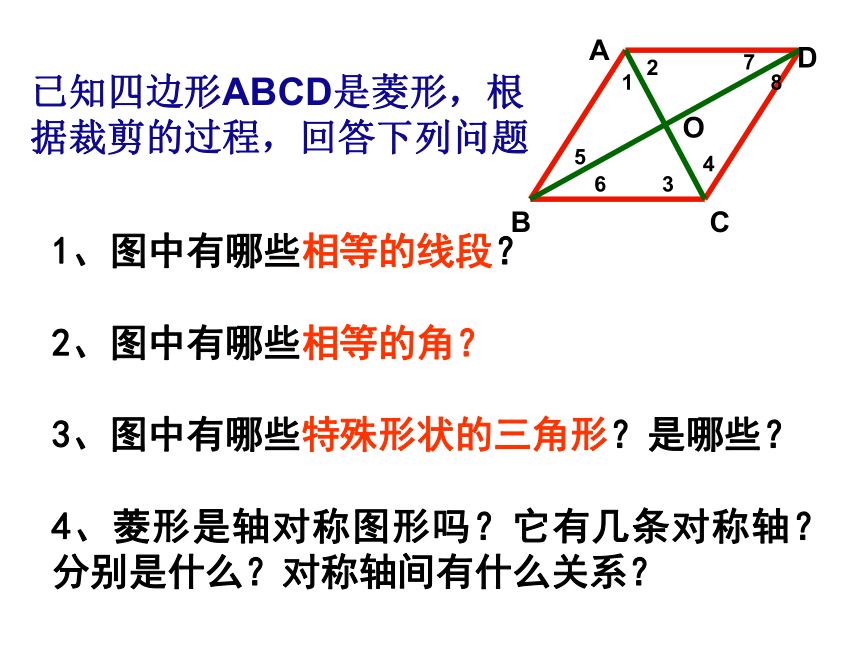
已知四边形ABCD是菱形,根据裁剪的过程,回答下列问题
A
B
C
D
O
1
2
3
4
5
6
7
8
1、图中有哪些相等的线段?
2、图中有哪些相等的角?
3、图中有哪些特殊形状的三角形?是哪些?
4、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?
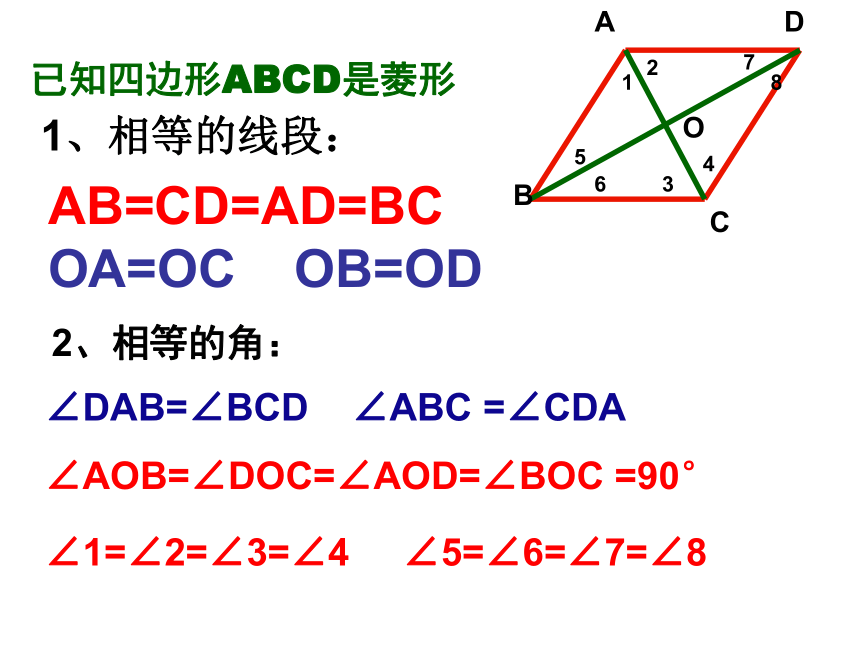
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
1、相等的线段:
AB=CD=AD=BC
OA=OC OB=OD
2、相等的角:
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
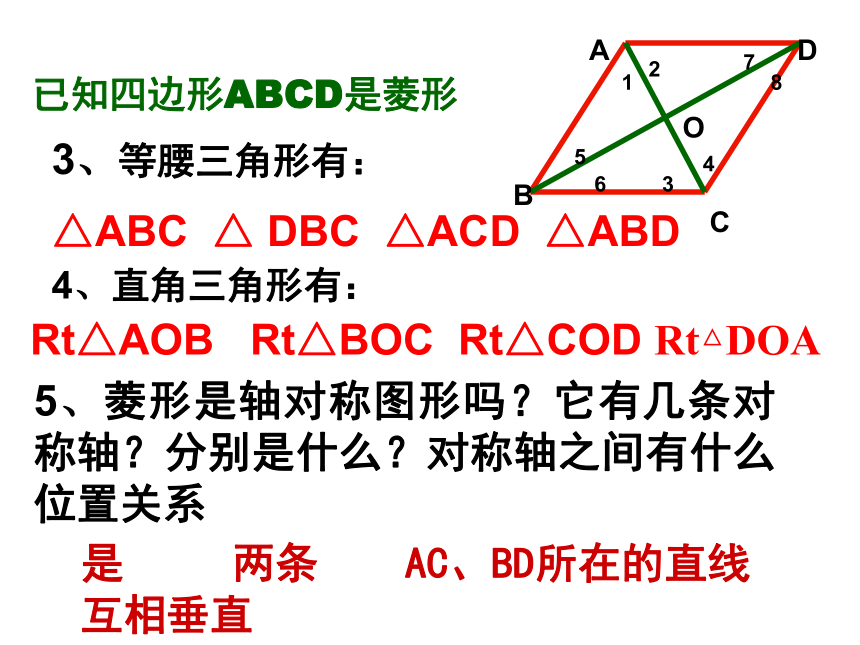
3、等腰三角形有:
△ABC △ DBC △ACD △ABD
4、直角三角形有:
Rt△AOB Rt△BOC Rt△COD Rt△DOA
5、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴之间有什么位置关系
是 两条 AC、BD所在的直线 互相垂直
A
B
C
D
O
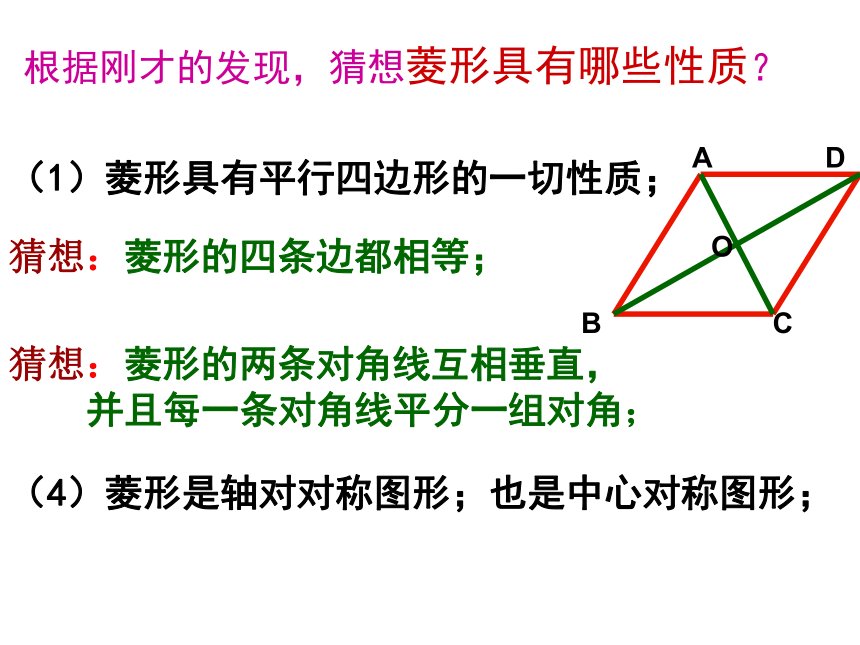
根据刚才的发现,猜想菱形具有哪些性质?
(1)菱形具有平行四边形的一切性质;
猜想:菱形的四条边都相等;
猜想:菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;
(4)菱形是轴对对称图形;也是中心对称图形;
命题: 菱形的四条边都相等。
已知:如图,四边ABCD是菱形
求证:AB=BC=CD=AD
证明:∵四边形ABCD是平行四边形
∴ AB=CD AD=BC (平行四 边形的两组对边分别相等)
∵ AB=AD
∴ AB=BC=CD=AD
A
B
C
D
已知:在□ABCD中,AB=AD
已知:菱形ABCD的对角线AC和BD相交于点O,如下图,
证明:∵四边形ABCD是菱形
A
B
C
D
O
∴ △ABD是等腰三角形
∵BO=DO
∴AB=AD ,BO=DO
∴AC⊥BD
即,AC平分∠BAD
同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC
命题:菱形的对角线互相垂直,
并且每一条对角线平分一组对角;
【菱形的面积公式】
菱形是特殊的平行四边形,
利用平行四边形面积公式计算
菱形的面积
S菱形=BC× AE
想一想:已知菱形的两条对角线的长,能求出它的面积吗
= S△ABD+S△BCD = AC×BD
S菱形ABCD
菱形的面积=底×高=对角线乘积的一半
A
B
C
D
O
E
菱形的两条对角线互相平分
菱形的对边平行
边
对角线
角
菱形的四条边相等
菱形的对角相等
菱形的邻角互补
菱形的两条对角线互相垂直,
每一条对角线平分一组对角。
A
D
C
B
O
菱形的面积=底×高=对角线乘积的一半
A
D
C
B
O
∵四边形ABCD是菱形,
说说理由:
∴AD∥BC,AB∥CD ( )
AB=BC=CD=DA ( )
OA=OC,OB=OD ( )
AC⊥BD ( )
∠ADB=∠CDB=∠ABD=∠CBD
= ∠ADC= ∠ABC ( )
你都掌握了吗?
1.已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中∠ABC=60度,则∠BAC=_______。
3cm
60度
3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )
C
A.10cm B.7cm C. 5cm D.4cm
A
B
C
D
O
3
4
有关菱形问题可转化为直角三角形或
等腰三角形的问题来解决
A
B
C
D
例2:如图,菱形花坛ABCD的周长为80m, ∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积( 分别精确到0.01m和0.01m )
2
O
解:∵ 花坛ABCD是菱形
∴ AC⊥BD, ∠ABO = ∠ABC = ×60°=30°
AB = BC = CD = AD = ×80 = 20 (m)
在Rt△OAB中,AO= AB= ×20=10(m)
BO= ≈17.32(m)
∴ 花坛的两条小路长
AC = 2AO = 20 (m)
BD = 2BO ≈34.64(m)
花坛的面积 = AC·BD≈346.4 ( )
4、已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。
A
B
C
D
E
O
A
B
C
D
E
O
2
∵四边形ABCD是菱形, ∴AD=AB
解:
∴AD=AB=BD
∵ E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB 的中垂线)
∴ ∠DAB= 60 °, ∴ ∠ABC=120 °
(2)
∵AE=2, ∴ AB=4 ∴ BD=AB=4
∵四边形ABCD是菱形,∴ AC⊥DB
∵ DB=4 ∴ 0B=2
∴ 在R t△AOB中,由勾股定理得
2
AO=
∴ AC=4
(3)
在Rt△DAE中,由勾股定理得
DE=
=2
∴ S菱形ABCD=4×2
=8
(1)
已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD;
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
D
C
B
A
在任意四边形ABCD中,对角线AC⊥BD ,且AC=18,BD=10。问四边形ABCD的面积是多少?
ABCD=S△ABD+S△BCD
S
=
BD·AO
+
BD·CO
=
·BD· (AO+CO)
=
BD·AC
=
×10×18=90
解:
D
A
O
B
C
你有什么
发现?
如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。
A
B
C
D
E
F
你敢挑战吗?回去想一想
菱形性质的应用
已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.
求:(1).对角线AC的长度; (2).菱形的面积
解:(1)
∵四边形ABCD是菱形,
=2×△ABD的面积
∴∠AED=900,
(2)菱形ABCD的面积=△ABD的面积+△CBD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
1个定义
2个公式
3个特性
:有一组邻边相等的平行四边形叫菱形
:S菱形=底×高
S菱形= 对角线乘积的一半
:特在“边、对角线、对称性”
作业
习题19.2第5,11,12题
人教版数学教材八年级下
19.2特殊的平行四边形
19.2.2菱形的性质
观 察
下面的图形中有你熟悉的吗?
三菱汽车标志欣赏
读一读
越王勾践剑,一把在地下埋藏了2000多年的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列的黑色菱形暗花纹。
平行四边形再认识
一组邻边相等的平行四边形叫做菱形
AB=BC
四边形ABCD是菱形
□ABCD
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?从这个图形中你有什么发现?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
已知四边形ABCD是菱形,根据裁剪的过程,回答下列问题
A
B
C
D
O
1
2
3
4
5
6
7
8
1、图中有哪些相等的线段?
2、图中有哪些相等的角?
3、图中有哪些特殊形状的三角形?是哪些?
4、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
1、相等的线段:
AB=CD=AD=BC
OA=OC OB=OD
2、相等的角:
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
3、等腰三角形有:
△ABC △ DBC △ACD △ABD
4、直角三角形有:
Rt△AOB Rt△BOC Rt△COD Rt△DOA
5、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴之间有什么位置关系
是 两条 AC、BD所在的直线 互相垂直
A
B
C
D
O
根据刚才的发现,猜想菱形具有哪些性质?
(1)菱形具有平行四边形的一切性质;
猜想:菱形的四条边都相等;
猜想:菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;
(4)菱形是轴对对称图形;也是中心对称图形;
命题: 菱形的四条边都相等。
已知:如图,四边ABCD是菱形
求证:AB=BC=CD=AD
证明:∵四边形ABCD是平行四边形
∴ AB=CD AD=BC (平行四 边形的两组对边分别相等)
∵ AB=AD
∴ AB=BC=CD=AD
A
B
C
D
已知:在□ABCD中,AB=AD
已知:菱形ABCD的对角线AC和BD相交于点O,如下图,
证明:∵四边形ABCD是菱形
A
B
C
D
O
∴ △ABD是等腰三角形
∵BO=DO
∴AB=AD ,BO=DO
∴AC⊥BD
即,AC平分∠BAD
同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ;
AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC
命题:菱形的对角线互相垂直,
并且每一条对角线平分一组对角;
【菱形的面积公式】
菱形是特殊的平行四边形,
利用平行四边形面积公式计算
菱形的面积
S菱形=BC× AE
想一想:已知菱形的两条对角线的长,能求出它的面积吗
= S△ABD+S△BCD = AC×BD
S菱形ABCD
菱形的面积=底×高=对角线乘积的一半
A
B
C
D
O
E
菱形的两条对角线互相平分
菱形的对边平行
边
对角线
角
菱形的四条边相等
菱形的对角相等
菱形的邻角互补
菱形的两条对角线互相垂直,
每一条对角线平分一组对角。
A
D
C
B
O
菱形的面积=底×高=对角线乘积的一半
A
D
C
B
O
∵四边形ABCD是菱形,
说说理由:
∴AD∥BC,AB∥CD ( )
AB=BC=CD=DA ( )
OA=OC,OB=OD ( )
AC⊥BD ( )
∠ADB=∠CDB=∠ABD=∠CBD
= ∠ADC= ∠ABC ( )
你都掌握了吗?
1.已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中∠ABC=60度,则∠BAC=_______。
3cm
60度
3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )
C
A.10cm B.7cm C. 5cm D.4cm
A
B
C
D
O
3
4
有关菱形问题可转化为直角三角形或
等腰三角形的问题来解决
A
B
C
D
例2:如图,菱形花坛ABCD的周长为80m, ∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积( 分别精确到0.01m和0.01m )
2
O
解:∵ 花坛ABCD是菱形
∴ AC⊥BD, ∠ABO = ∠ABC = ×60°=30°
AB = BC = CD = AD = ×80 = 20 (m)
在Rt△OAB中,AO= AB= ×20=10(m)
BO= ≈17.32(m)
∴ 花坛的两条小路长
AC = 2AO = 20 (m)
BD = 2BO ≈34.64(m)
花坛的面积 = AC·BD≈346.4 ( )
4、已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。
A
B
C
D
E
O
A
B
C
D
E
O
2
∵四边形ABCD是菱形, ∴AD=AB
解:
∴AD=AB=BD
∵ E是AB的中点,且DE⊥AB
∴DA=DB(DE为AB 的中垂线)
∴ ∠DAB= 60 °, ∴ ∠ABC=120 °
(2)
∵AE=2, ∴ AB=4 ∴ BD=AB=4
∵四边形ABCD是菱形,∴ AC⊥DB
∵ DB=4 ∴ 0B=2
∴ 在R t△AOB中,由勾股定理得
2
AO=
∴ AC=4
(3)
在Rt△DAE中,由勾股定理得
DE=
=2
∴ S菱形ABCD=4×2
=8
(1)
已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD;
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
D
C
B
A
在任意四边形ABCD中,对角线AC⊥BD ,且AC=18,BD=10。问四边形ABCD的面积是多少?
ABCD=S△ABD+S△BCD
S
=
BD·AO
+
BD·CO
=
·BD· (AO+CO)
=
BD·AC
=
×10×18=90
解:
D
A
O
B
C
你有什么
发现?
如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。
A
B
C
D
E
F
你敢挑战吗?回去想一想
菱形性质的应用
已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.
求:(1).对角线AC的长度; (2).菱形的面积
解:(1)
∵四边形ABCD是菱形,
=2×△ABD的面积
∴∠AED=900,
(2)菱形ABCD的面积=△ABD的面积+△CBD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
1个定义
2个公式
3个特性
:有一组邻边相等的平行四边形叫菱形
:S菱形=底×高
S菱形= 对角线乘积的一半
:特在“边、对角线、对称性”
作业
习题19.2第5,11,12题
