第三章 勾股定理 3.3勾股定理的应用 苏科版数学八年级上册(共20张)
文档属性
| 名称 | 第三章 勾股定理 3.3勾股定理的应用 苏科版数学八年级上册(共20张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 13:14:15 | ||
图片预览






文档简介
(共20张PPT)
勾
股
定理的
3.3
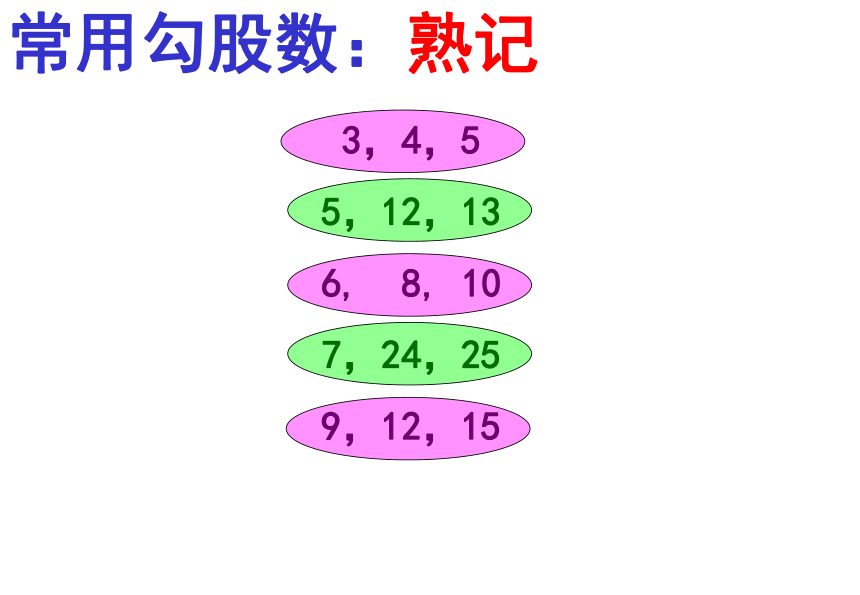
直角三角形两条直角边的平方和等于斜边的平方。
c
a
b
A
B
C
∵
在Rt△ABC中,
∠C=90?
,AB=c,AC=b,BC=a,
?
a2+b2=c2.
┏
勾股定理:
几何语言:
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
∵
△ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,
?∠C=90?
(△ABC是直角三角形)
.
c
a
b
A
B
C
勾股逆定理:
几何语言:
3,4,5
5,12,13
6,
8,
10
7,24,25
9,12,15
常用勾股数:熟记
2.若直角三角形的三边长分别为3,4,x,则x值为_____.
x
4
3
┏
x
4
3
┏
解:如图,当X为斜边时,X=5
;
当X为直角边时,X=√7
.
1.
已知直角三角形ABC中,∠C=900:
①a=5,b=12,则c=____;
②a=6,c=10,则b=____;
③b=7,c=25,则a=____;
小试牛刀
3.
已知直角三角形ABC中,∠C=900:
①a=6,b:c=4:5,则b、c分别为多少?
②a=7,c比b多了1,则b、c分别为多少?
方程的思想:
①中设b为4x,则c为5x;
②中设b为x,则c为x+1。
再由勾股定理列方程
例1.小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度。
A
B
C
5
方程的思想:
┏
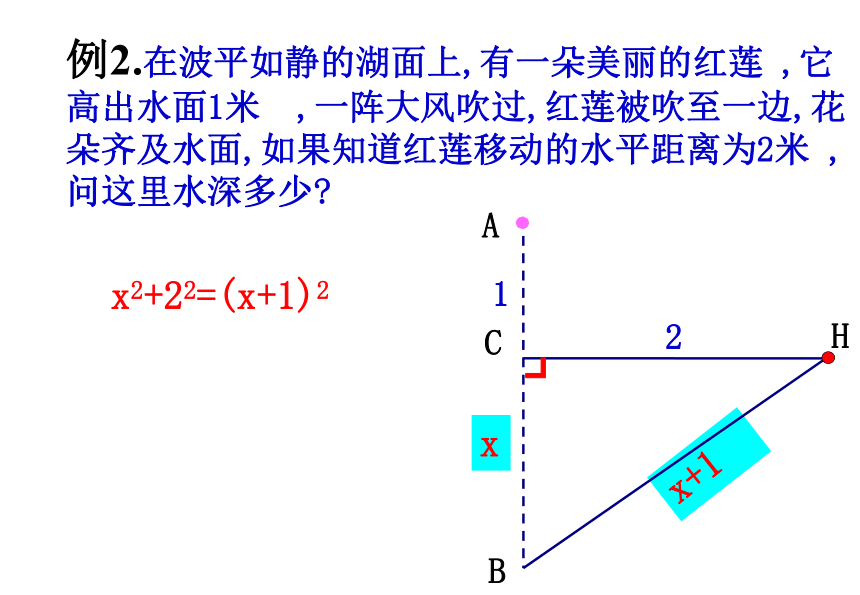
例2.在波平如静的湖面上,有一朵美丽的红莲
,它高出水面1米
,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米
,问这里水深多少?
x+1
B
C
A
H
1
2
?
┓
x
x2+22=(x+1)2
例3.如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
A
B
D
E
C
例4.已知:如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8cm
,BC=10cm,求EC的长
A
B
C
D
E
F
例5.某农民开垦出一块三边长分别为13m,15m,14m三角形地块准备种植花生,聪明的同学你能帮他算一算这块地的面积吗?
不是直角三角形怎么办呢?
14
15
13
C
B
A
14
15
13
C
B
A
我有办法可以把它转化为直角三角形,问题不就容易了吗?
D
┏
补1.一种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面露出5㎝,问吸管要做多长?
A
B
C
补2.做一个长,宽,高分别为4厘米,3厘米,
12厘米的木箱,一根长为12.5厘米的木棒能否放
入,为什么?试用今天学过的知识说明。
拓展
4
3
12
12
A
B
C
A
B
C
D
B
4
3
D
C
x
小结:
(在直角三角形中,知道一边及另两边关系,可以求出未知的两边.)
A
B
我怎么走
会最近呢?
附加题:有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B
,
蚂蚁沿着圆柱侧面爬行的最短路程是多少?
(π的值取3)
B
A
高
12cm
B
A
长18cm
(π的值取3)
9cm
∵
AB2=92+122=81+144=225=
∴
AB=15(cm)
蚂蚁爬行的最短路程是15厘米.
152
勾
股
定理的
3.3
直角三角形两条直角边的平方和等于斜边的平方。
c
a
b
A
B
C
∵
在Rt△ABC中,
∠C=90?
,AB=c,AC=b,BC=a,
?
a2+b2=c2.
┏
勾股定理:
几何语言:
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
∵
△ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,
?∠C=90?
(△ABC是直角三角形)
.
c
a
b
A
B
C
勾股逆定理:
几何语言:
3,4,5
5,12,13
6,
8,
10
7,24,25
9,12,15
常用勾股数:熟记
2.若直角三角形的三边长分别为3,4,x,则x值为_____.
x
4
3
┏
x
4
3
┏
解:如图,当X为斜边时,X=5
;
当X为直角边时,X=√7
.
1.
已知直角三角形ABC中,∠C=900:
①a=5,b=12,则c=____;
②a=6,c=10,则b=____;
③b=7,c=25,则a=____;
小试牛刀
3.
已知直角三角形ABC中,∠C=900:
①a=6,b:c=4:5,则b、c分别为多少?
②a=7,c比b多了1,则b、c分别为多少?
方程的思想:
①中设b为4x,则c为5x;
②中设b为x,则c为x+1。
再由勾股定理列方程
例1.小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度。
A
B
C
5
方程的思想:
┏
例2.在波平如静的湖面上,有一朵美丽的红莲
,它高出水面1米
,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米
,问这里水深多少?
x+1
B
C
A
H
1
2
?
┓
x
x2+22=(x+1)2
例3.如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
A
B
D
E
C
例4.已知:如图所示,折叠长方形的一边AD,使点D落在BC边的点F处,已知AB=8cm
,BC=10cm,求EC的长
A
B
C
D
E
F
例5.某农民开垦出一块三边长分别为13m,15m,14m三角形地块准备种植花生,聪明的同学你能帮他算一算这块地的面积吗?
不是直角三角形怎么办呢?
14
15
13
C
B
A
14
15
13
C
B
A
我有办法可以把它转化为直角三角形,问题不就容易了吗?
D
┏
补1.一种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面露出5㎝,问吸管要做多长?
A
B
C
补2.做一个长,宽,高分别为4厘米,3厘米,
12厘米的木箱,一根长为12.5厘米的木棒能否放
入,为什么?试用今天学过的知识说明。
拓展
4
3
12
12
A
B
C
A
B
C
D
B
4
3
D
C
x
小结:
(在直角三角形中,知道一边及另两边关系,可以求出未知的两边.)
A
B
我怎么走
会最近呢?
附加题:有一个圆柱,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面上的A点有一只蚂蚁,它想从点A爬到点B
,
蚂蚁沿着圆柱侧面爬行的最短路程是多少?
(π的值取3)
B
A
高
12cm
B
A
长18cm
(π的值取3)
9cm
∵
AB2=92+122=81+144=225=
∴
AB=15(cm)
蚂蚁爬行的最短路程是15厘米.
152
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
