第三章 勾股定理 3.3勾股定理的应用 课件 苏科版数学八年级上册 (共21张)
文档属性
| 名称 | 第三章 勾股定理 3.3勾股定理的应用 课件 苏科版数学八年级上册 (共21张) |  | |
| 格式 | zip | ||
| 文件大小 | 669.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 13:21:47 | ||
图片预览



文档简介
(共21张PPT)
初中数学八年级上册
(苏科版)
3.3勾股定理的应用
学习目标
通过构造直角三角形,运用勾股定理解决较复杂的实际问题。
c
b
a
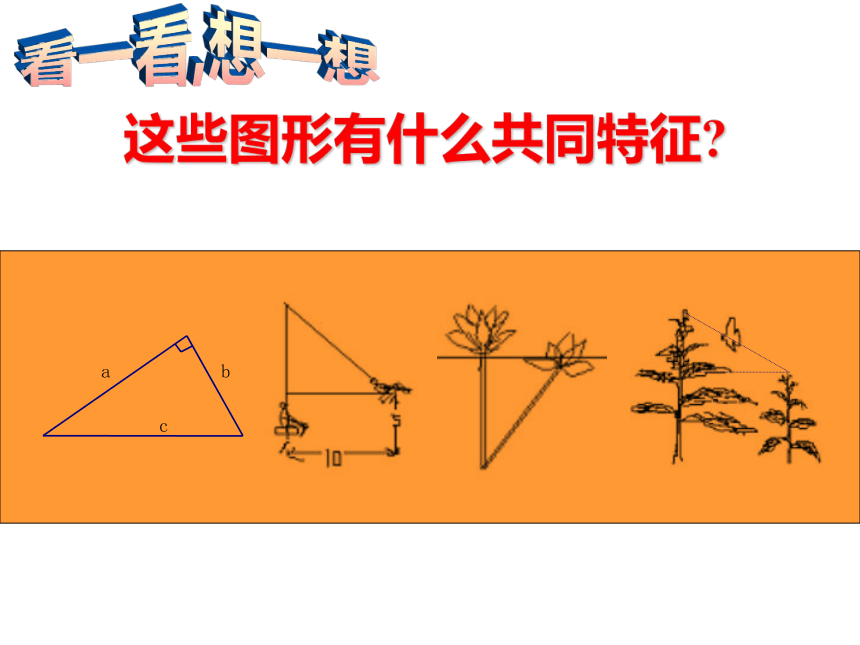
这些图形有什么共同特征?
问题
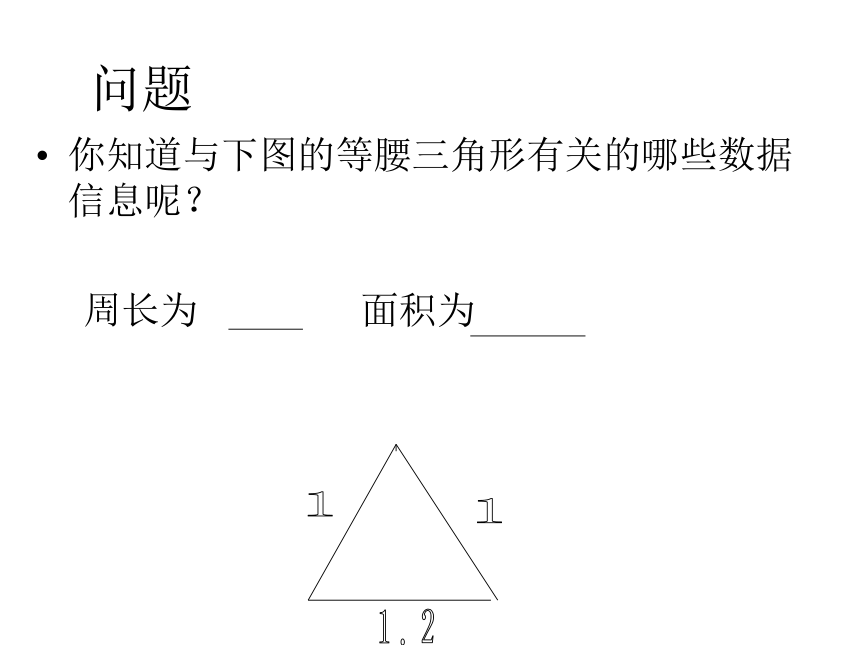
你知道与下图的等腰三角形有关的哪些数据信息呢?
周长为
面积为
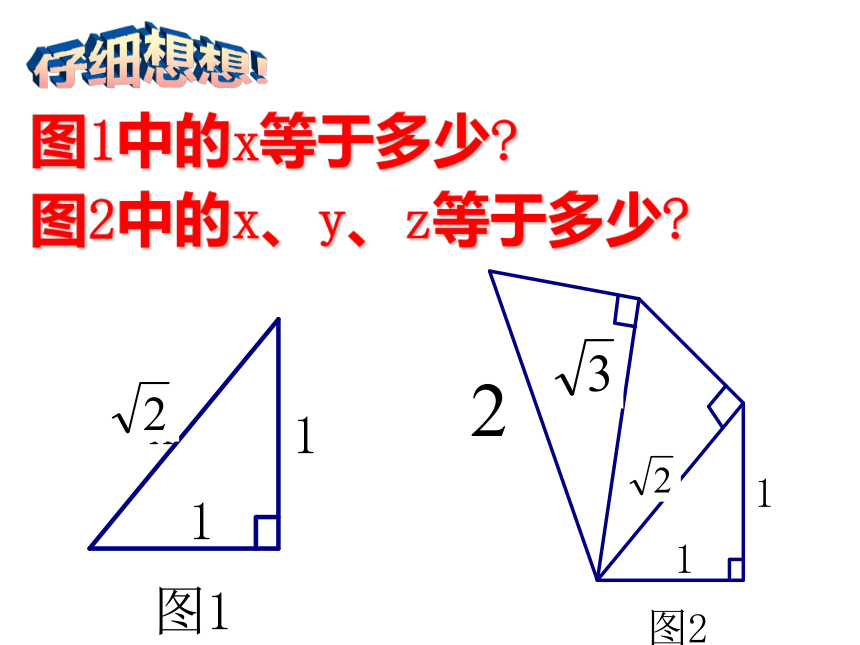
图1中的x等于多少?
图2中的x、y、z等于多少?
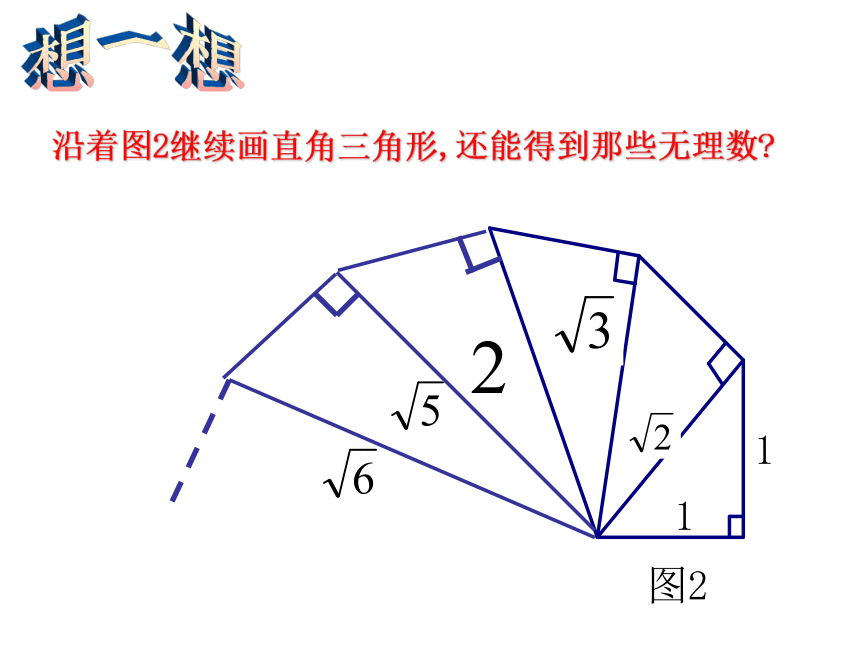
沿着图2继续画直角三角形,还能得到那些无理数?
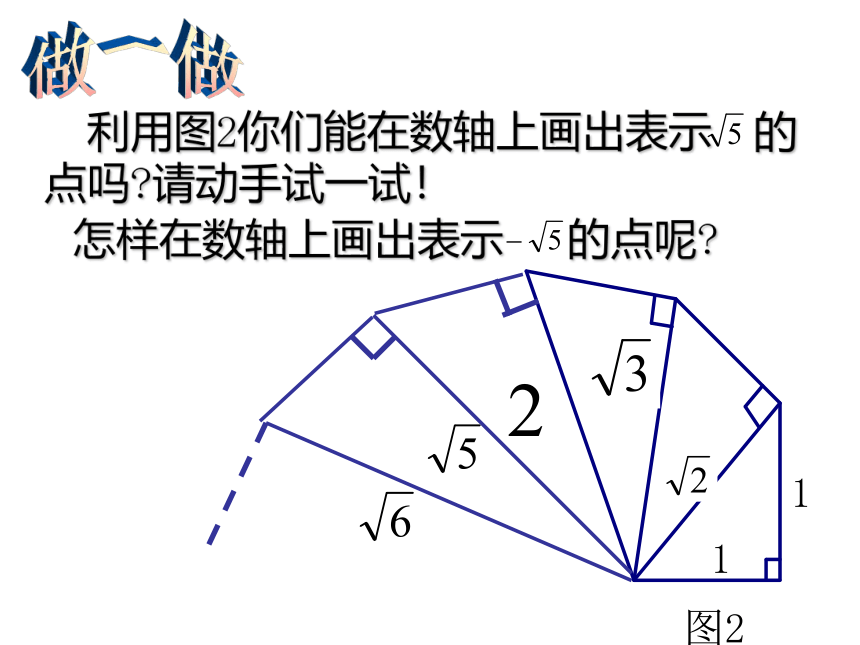
利用图2你们能在数轴上画出表示
的点吗?请动手试一试!
怎样在数轴上画出表示
的点呢?
在数轴上表示
,
的点怎样画出?
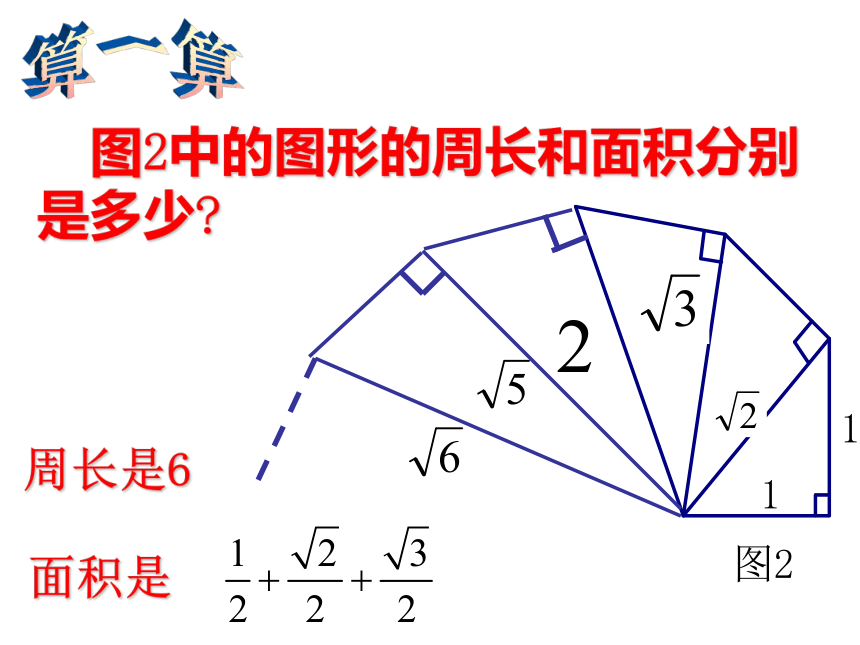
图2中的图形的周长和面积分别是多少?
周长是6
面积是
你们能说出
的实际意义吗?
如图,求四边形ABCD的周长和面积。
周长是68;
面积是246;
例1、如图,等边三角形ABC的边长是6,求△ABC的面积。
解:作AD⊥BC,
∵△ABC是等边三角形,
∴
在Rt△ABC中,
∴
1、如图5,在△ABC中,AB=AC=17,BC=16,求△ABC的面积。
2、如图6,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13,求△ABC的周长和面积。
材料1:如图7,在△ABC中,AB=25,BC=7,AC=24,问△ABC是什么三角形?
材料2:如图8,在△ABC中,AB=26,BC=20,BC边上的中线AD=24,求AC.
,
解:∵AD是BC边上的中线,
∴
∵
∴
∴∠ADB=90°,
∴AD⊥BC,
∴AD是BC的垂直平线,
∴AC=AB=26.
材料3:
如图9,在△ABC中,
AB=15,AD=12,BD=9,AC=13,求△ABC的周长和面积。
周长为42
面积为84
自学检测
1.已知四边形ABCD,∠B=90°,各边尺寸如图所示,你能求出∠BAD的度数吗?
A
2
2
3
1
B
C
D
┓
勾股定理与它的逆定理在应用上有什么区别?
勾股定理主要应用于求线段的长度、图形的周长、面积;
勾股定理的逆定理用于判断三角形的形状。
如图,以△ABC的三边为直径向外作半圆,且S1+S3=S2,试判断△ABC的形状?
S1
S2
S3
勾
股
定
理
的
应
用
表示无理数
勾
股
定
理
的
逆
定
理
的
应
用
数
形
结
合
思
想
转
化
思
想
1、数形结合思想
2、转化思想
3、勾股定理与其逆定理在应用上的区别
初中数学八年级上册
(苏科版)
3.3勾股定理的应用
学习目标
通过构造直角三角形,运用勾股定理解决较复杂的实际问题。
c
b
a
这些图形有什么共同特征?
问题
你知道与下图的等腰三角形有关的哪些数据信息呢?
周长为
面积为
图1中的x等于多少?
图2中的x、y、z等于多少?
沿着图2继续画直角三角形,还能得到那些无理数?
利用图2你们能在数轴上画出表示
的点吗?请动手试一试!
怎样在数轴上画出表示
的点呢?
在数轴上表示
,
的点怎样画出?
图2中的图形的周长和面积分别是多少?
周长是6
面积是
你们能说出
的实际意义吗?
如图,求四边形ABCD的周长和面积。
周长是68;
面积是246;
例1、如图,等边三角形ABC的边长是6,求△ABC的面积。
解:作AD⊥BC,
∵△ABC是等边三角形,
∴
在Rt△ABC中,
∴
1、如图5,在△ABC中,AB=AC=17,BC=16,求△ABC的面积。
2、如图6,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13,求△ABC的周长和面积。
材料1:如图7,在△ABC中,AB=25,BC=7,AC=24,问△ABC是什么三角形?
材料2:如图8,在△ABC中,AB=26,BC=20,BC边上的中线AD=24,求AC.
,
解:∵AD是BC边上的中线,
∴
∵
∴
∴∠ADB=90°,
∴AD⊥BC,
∴AD是BC的垂直平线,
∴AC=AB=26.
材料3:
如图9,在△ABC中,
AB=15,AD=12,BD=9,AC=13,求△ABC的周长和面积。
周长为42
面积为84
自学检测
1.已知四边形ABCD,∠B=90°,各边尺寸如图所示,你能求出∠BAD的度数吗?
A
2
2
3
1
B
C
D
┓
勾股定理与它的逆定理在应用上有什么区别?
勾股定理主要应用于求线段的长度、图形的周长、面积;
勾股定理的逆定理用于判断三角形的形状。
如图,以△ABC的三边为直径向外作半圆,且S1+S3=S2,试判断△ABC的形状?
S1
S2
S3
勾
股
定
理
的
应
用
表示无理数
勾
股
定
理
的
逆
定
理
的
应
用
数
形
结
合
思
想
转
化
思
想
1、数形结合思想
2、转化思想
3、勾股定理与其逆定理在应用上的区别
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
