四川省仁寿县2020-2021学年高二下学期6月联考数学(文)试题 Word版含答案
文档属性
| 名称 | 四川省仁寿县2020-2021学年高二下学期6月联考数学(文)试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 604.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 00:00:00 | ||
图片预览



文档简介
仁寿县2020-2021学年高二下学期6月联考
文科数学
2021.06
数学试题卷(文科)共4页.满分150分.考试时间120分钟.
注意事项:
1.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号.
2.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上.
3.所有题目必须在答题卡上作答,在试题卷上答题无效.
4.考试结束后,将答题卡交回.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个备选项中,只有一项是符合题目要求的.
1.已知i为虚数单位,复数false,false,若z为纯虚数,则false( )
A.false B.false C.2 D.false
2.某学校决定从该校的2000名高一学生中采用系统抽样(等距)的方法抽取50名学生进行体质分析,现将2000名学生从1至2000编号,已知样本中第一个编号为7,则抽取的第26个学生的编号为( )
A.997 B.1007 C.1047 D.1087
3.2020年初,从非洲蔓延到东南亚的蝗虫灾害严重威胁了国际农业生产,影响了人民生活.世界性与区域性温度的异常?早涝频繁发生给蝗灾发生创造了机会.已知蝗虫的产卵量false与温度false的关系可以用模型false拟合,设false,其变换后得到一组数据:
false
false
false
false
false
1756410129540false
false
false
false
false
false
false
由上表可得线性回归方程false,则false( )
A.false B.false C.false D.false
4.甲、乙两名同学在高考前的5次模拟考中的数学成绩如茎叶图所示,记甲、 乙两人的平均成绩分别为false,下列说法正确的是( )
A.false,且乙比甲的成绩稳定 B.false,且乙比甲的成绩稳定
C.false,且甲比乙的成绩稳定 D.false,且甲比乙的成绩稳定
5.2021年电影春节档票房再创新高,其中电影《唐人街探案3》和《你好,李焕英》是今年春节档电影中最火爆的两部电影,这两部电影都是2月12日(大年初一)首映,根据猫眼票房数据得到如下统计图,该图统计了从2月12日到2月18日共计7天的累计票房(单位:亿元),则下列说法中错误的是( )
4410075217805
A.这7天电影《你好,李焕英》每天的票房都超过2.5亿元
B.这7天两部电影的累计票房的差的绝对值先逐步扩大后逐步缩小
C.这7天电影《你好,李焕英》的当日票房占比逐渐增大
D.这7天中有4天电影《唐人街探案3》的当日票房占比超过50%
6.如图所示的程序框图,若输入x的值为2,输出v的值为16,则判断框内可以填入( )
A.k≤3? B.k≤4? C.k≥3? D.k≥4?
7.函数false的零点个数为( )
A.false B.false或false C.false或false D.false或false或false
8.苏格兰数学家科林麦克劳林(ColinMaclaurin)研究出了著名的Maclaurin级数展开式,受到了世界上顶尖数学家的广泛认可,下面是麦克劳林建立的其中一个公式:false,试根据此公式估计下面代数式false的近似值为( )(可能用到数值ln2.414=0.881,ln3.414=1.23)
A.3.23 B.2.881 C.1.881 D.1.23
9.函数false(其中false为自然对数的底数)的图象大致是( )
A. B. C. D.
10.甲乙两人相约10天内在某地会面,约定先到的人等候另一个人,经过三天后方可离开.若他们在期限内到达目的地是等可能的,则此二人会晤的概率是( )
A.0.5 B.0.51 C.0.75 D.0.4
11.设函数false是奇函数false的导函数,false.当false时,false,则使得false成立的false的取值范围是( )
A.false B.false C.false D.false
12.已知函数false,false,设false为实数,若存在实数false,使false,则实数false的取值范围为( )
A.false B.false C.false D.false
二、填空题:本大题共4小题,每小题5分,共20分. 请将答案填在答题卷中的相应位置.
13.false的边false,false为边false上一动点,则false的概率为__▲___
14.复数false(false是虚数单位)是方程false的一个根,则实数false___▲___
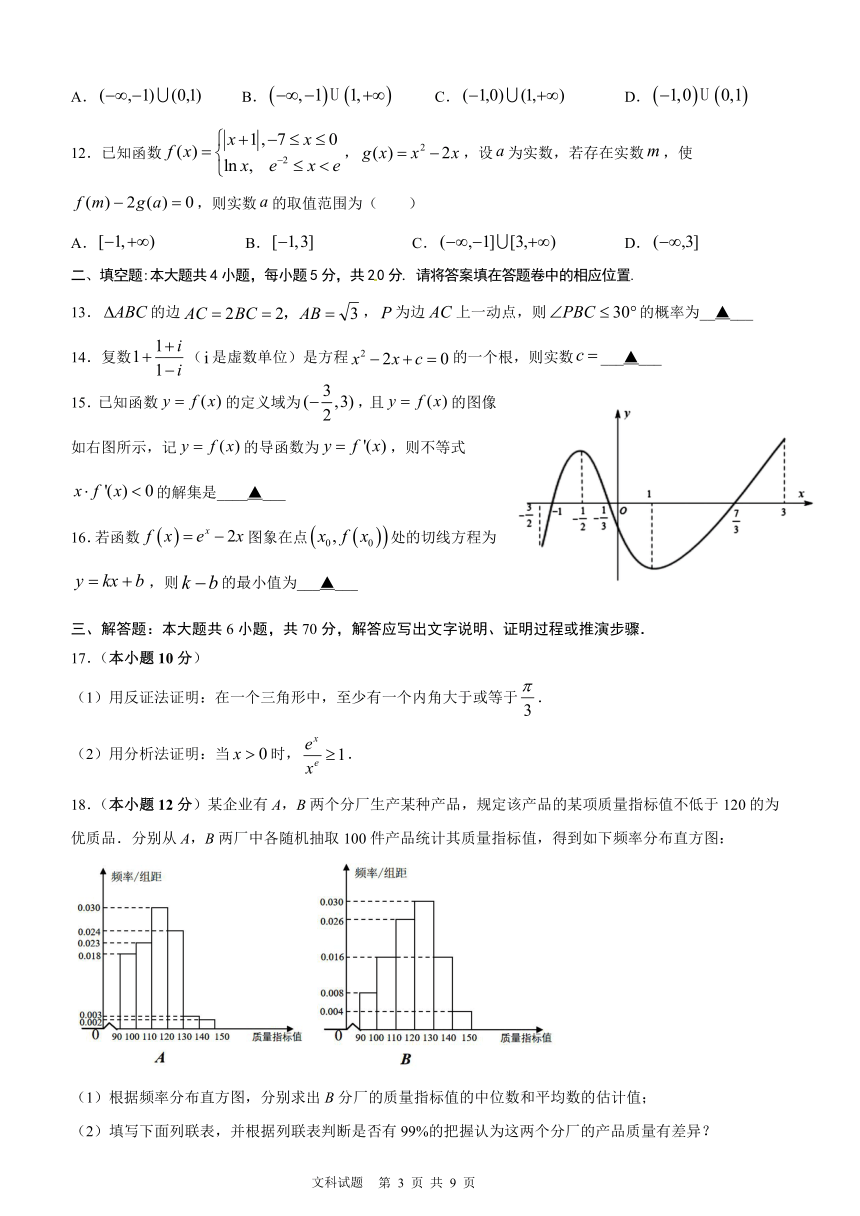
385699016383015.已知函数false的定义域为false,且false的图像如右图所示,记false的导函数为false,则不等式false的解集是____▲___
16.若函数false图象在点false处的切线方程为false,则false的最小值为___▲___
三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或推演步骤.
17.(本小题10分)
(1)用反证法证明:在一个三角形中,至少有一个内角大于或等于false.
(2)用分析法证明:当false时,false.
18.(本小题12分)某企业有A,B两个分厂生产某种产品,规定该产品的某项质量指标值不低于120的为优质品.分别从A,B两厂中各随机抽取100件产品统计其质量指标值,得到如下频率分布直方图:
根据频率分布直方图,分别求出B分厂的质量指标值的中位数和平均数的估计值;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为这两个分厂的产品质量有差异?
3067050128270
19.(本小题12分)已知函数false.
(1)求曲线false在false处的切线方程;
(2)求曲线false过点false的切线方程.
3524250270510
20.(本小题12分)某工厂为了对新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组检测数据false如表所示:
已知变量false具有线性负相关关系,且false,现有甲?乙?丙三位同学通过计算求得其回归直线方程分别为:甲false;乙false;丙false,其中有且仅有一位同学的计算结果是正确的.
(1)试判断谁的计算结果正确?并求出false的值;
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”.现从检测数据中随机抽取2个,求“理想数据”至少有一个的概率.
21.(本小题12分)已知函数false.
(1)求函数false的最值;
(2)求证:false.
22.(本小题12分)已知函数falsefalse为自然对数的底数).
(1)若false是false的极值点,求false的取值;
(2)若false只有一个零点,求false的取值范围.
仁寿县2020-2021学年高二下学期6月联考
文科数学参考答案
选择题
1.C 2.B 3.B 4.A 5.D 6.A 7.A 8.B 9.C 10.B 11.C 12.B
填空题
13.false 14.false 15.false 16.false
解答题
17.解:(1)证明:假设三角形三个角false都小于false·············································1分
那么false····························································································2分
而三角形内角和false与假设矛盾·····························································3分
所以三角形至少有一个内角大于或等于false·····························································4分
(2)证明:要证false(false),只需证false·····················································5分
则需证false,即false··········································································7分
令false,则false,当false时,false;当false时,false,所以false,即false,则原不等式得证··················································10分
18.解:(1)B分厂的质量指标值;
由false,则false的中位数为false······································2分
false的平均数为false·········6分
(2)false列联表:
···············································································7分
由列联表可知false的观测值为:
false··································11分
所以有99%的把握认为两个分厂的产品质量有差异.················································12分
19.解:(1)由已知得false,则false,所以切线斜率false,···························2分
因为false,所以切点坐标为false,·····················································4分
所以所求直线方程为false,
故曲线false在false处的切线方程为false.·······················································5分
(2)由已知得false,设切点为false,···················································6分
则false,即false,得false或false,
所以切点为false或false,切线的斜率为false或false,·················································10分
所以切线方程为false或false
即切线方程为false或false·······························································12分
20.解:(1)∵变量false具有线性负相关关系,∴甲是错误的.······································1分
又∵false∴false,满足方程false,故乙是正确的.··········3分
由false得false··································································5分
(2)由计算可得“理想数据”有false个,即false,则用字母false代表“理想数据”,其余检测数据用false代表,·················································································7分
所以从检测数中随机抽取false个有false,false,false,false,false,false,false,false,false,false,false,false,false,false,false共false种,······························································································10分
满足题意的有false,false,false,false,false,false,false,false,false,false,false,false共false种,·········11分
所以“理想数据”至少有一个的概率为false····························································12分
21.解:(1)由题可知false··································································1分
所以false,当false时,false,false单调递减;当false时,false,false单调递增,所以false··································································4分
(2)方法一:false,令false,
false,故false在false上单调递增.············································5分
又false,又false在false上连续,
false使得false,即false,falsefalse.(*)·····························7分
false随false的变化情况如下:
false
false
false
false
false
false
false
false
false
↘
极小值
↗
falsefalse. 由(*)式得false,代入上式得
false. 令false,
false,故false在false上单调递减.false,又false,.
即falsefalse.·················································································12分
方法二:falsefalse,································································8分
易得false,false,
所以false,得证false······················································12分
22.解:(1)false,······································································1分
当false时,false,false;false,false,此时false恒成立,则false不是函数false的极值点·······················································································3分
所以false···············································································4分
(2)false只有一个零点,显然是false,所以分为两种情况
第1种情况:false满足false,此时false·····················································6分
第2种情况:false无解,
令false,false;
①当false时,false,false单调递增false,故在false上存在false使得false;·························································································8分
②当false时,方程false显然无解;·······························································9分
③当false时,false解得false,当false时,false,false单调递减;当false时,false,false单调递增,则false,即false,所以false·································································································11分
综上所述:false················································································12分
文科数学
2021.06
数学试题卷(文科)共4页.满分150分.考试时间120分钟.
注意事项:
1.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号.
2.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上.
3.所有题目必须在答题卡上作答,在试题卷上答题无效.
4.考试结束后,将答题卡交回.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个备选项中,只有一项是符合题目要求的.
1.已知i为虚数单位,复数false,false,若z为纯虚数,则false( )
A.false B.false C.2 D.false
2.某学校决定从该校的2000名高一学生中采用系统抽样(等距)的方法抽取50名学生进行体质分析,现将2000名学生从1至2000编号,已知样本中第一个编号为7,则抽取的第26个学生的编号为( )
A.997 B.1007 C.1047 D.1087
3.2020年初,从非洲蔓延到东南亚的蝗虫灾害严重威胁了国际农业生产,影响了人民生活.世界性与区域性温度的异常?早涝频繁发生给蝗灾发生创造了机会.已知蝗虫的产卵量false与温度false的关系可以用模型false拟合,设false,其变换后得到一组数据:
false
false
false
false
false
1756410129540false
false
false
false
false
false
false
由上表可得线性回归方程false,则false( )
A.false B.false C.false D.false
4.甲、乙两名同学在高考前的5次模拟考中的数学成绩如茎叶图所示,记甲、 乙两人的平均成绩分别为false,下列说法正确的是( )
A.false,且乙比甲的成绩稳定 B.false,且乙比甲的成绩稳定
C.false,且甲比乙的成绩稳定 D.false,且甲比乙的成绩稳定
5.2021年电影春节档票房再创新高,其中电影《唐人街探案3》和《你好,李焕英》是今年春节档电影中最火爆的两部电影,这两部电影都是2月12日(大年初一)首映,根据猫眼票房数据得到如下统计图,该图统计了从2月12日到2月18日共计7天的累计票房(单位:亿元),则下列说法中错误的是( )
4410075217805
A.这7天电影《你好,李焕英》每天的票房都超过2.5亿元
B.这7天两部电影的累计票房的差的绝对值先逐步扩大后逐步缩小
C.这7天电影《你好,李焕英》的当日票房占比逐渐增大
D.这7天中有4天电影《唐人街探案3》的当日票房占比超过50%
6.如图所示的程序框图,若输入x的值为2,输出v的值为16,则判断框内可以填入( )
A.k≤3? B.k≤4? C.k≥3? D.k≥4?
7.函数false的零点个数为( )
A.false B.false或false C.false或false D.false或false或false
8.苏格兰数学家科林麦克劳林(ColinMaclaurin)研究出了著名的Maclaurin级数展开式,受到了世界上顶尖数学家的广泛认可,下面是麦克劳林建立的其中一个公式:false,试根据此公式估计下面代数式false的近似值为( )(可能用到数值ln2.414=0.881,ln3.414=1.23)
A.3.23 B.2.881 C.1.881 D.1.23
9.函数false(其中false为自然对数的底数)的图象大致是( )
A. B. C. D.
10.甲乙两人相约10天内在某地会面,约定先到的人等候另一个人,经过三天后方可离开.若他们在期限内到达目的地是等可能的,则此二人会晤的概率是( )
A.0.5 B.0.51 C.0.75 D.0.4
11.设函数false是奇函数false的导函数,false.当false时,false,则使得false成立的false的取值范围是( )
A.false B.false C.false D.false
12.已知函数false,false,设false为实数,若存在实数false,使false,则实数false的取值范围为( )
A.false B.false C.false D.false
二、填空题:本大题共4小题,每小题5分,共20分. 请将答案填在答题卷中的相应位置.
13.false的边false,false为边false上一动点,则false的概率为__▲___
14.复数false(false是虚数单位)是方程false的一个根,则实数false___▲___
385699016383015.已知函数false的定义域为false,且false的图像如右图所示,记false的导函数为false,则不等式false的解集是____▲___
16.若函数false图象在点false处的切线方程为false,则false的最小值为___▲___
三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或推演步骤.
17.(本小题10分)
(1)用反证法证明:在一个三角形中,至少有一个内角大于或等于false.
(2)用分析法证明:当false时,false.
18.(本小题12分)某企业有A,B两个分厂生产某种产品,规定该产品的某项质量指标值不低于120的为优质品.分别从A,B两厂中各随机抽取100件产品统计其质量指标值,得到如下频率分布直方图:
根据频率分布直方图,分别求出B分厂的质量指标值的中位数和平均数的估计值;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为这两个分厂的产品质量有差异?
3067050128270
19.(本小题12分)已知函数false.
(1)求曲线false在false处的切线方程;
(2)求曲线false过点false的切线方程.
3524250270510
20.(本小题12分)某工厂为了对新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组检测数据false如表所示:
已知变量false具有线性负相关关系,且false,现有甲?乙?丙三位同学通过计算求得其回归直线方程分别为:甲false;乙false;丙false,其中有且仅有一位同学的计算结果是正确的.
(1)试判断谁的计算结果正确?并求出false的值;
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”.现从检测数据中随机抽取2个,求“理想数据”至少有一个的概率.
21.(本小题12分)已知函数false.
(1)求函数false的最值;
(2)求证:false.
22.(本小题12分)已知函数falsefalse为自然对数的底数).
(1)若false是false的极值点,求false的取值;
(2)若false只有一个零点,求false的取值范围.
仁寿县2020-2021学年高二下学期6月联考
文科数学参考答案
选择题
1.C 2.B 3.B 4.A 5.D 6.A 7.A 8.B 9.C 10.B 11.C 12.B
填空题
13.false 14.false 15.false 16.false
解答题
17.解:(1)证明:假设三角形三个角false都小于false·············································1分
那么false····························································································2分
而三角形内角和false与假设矛盾·····························································3分
所以三角形至少有一个内角大于或等于false·····························································4分
(2)证明:要证false(false),只需证false·····················································5分
则需证false,即false··········································································7分
令false,则false,当false时,false;当false时,false,所以false,即false,则原不等式得证··················································10分
18.解:(1)B分厂的质量指标值;
由false,则false的中位数为false······································2分
false的平均数为false·········6分
(2)false列联表:
···············································································7分
由列联表可知false的观测值为:
false··································11分
所以有99%的把握认为两个分厂的产品质量有差异.················································12分
19.解:(1)由已知得false,则false,所以切线斜率false,···························2分
因为false,所以切点坐标为false,·····················································4分
所以所求直线方程为false,
故曲线false在false处的切线方程为false.·······················································5分
(2)由已知得false,设切点为false,···················································6分
则false,即false,得false或false,
所以切点为false或false,切线的斜率为false或false,·················································10分
所以切线方程为false或false
即切线方程为false或false·······························································12分
20.解:(1)∵变量false具有线性负相关关系,∴甲是错误的.······································1分
又∵false∴false,满足方程false,故乙是正确的.··········3分
由false得false··································································5分
(2)由计算可得“理想数据”有false个,即false,则用字母false代表“理想数据”,其余检测数据用false代表,·················································································7分
所以从检测数中随机抽取false个有false,false,false,false,false,false,false,false,false,false,false,false,false,false,false共false种,······························································································10分
满足题意的有false,false,false,false,false,false,false,false,false,false,false,false共false种,·········11分
所以“理想数据”至少有一个的概率为false····························································12分
21.解:(1)由题可知false··································································1分
所以false,当false时,false,false单调递减;当false时,false,false单调递增,所以false··································································4分
(2)方法一:false,令false,
false,故false在false上单调递增.············································5分
又false,又false在false上连续,
false使得false,即false,falsefalse.(*)·····························7分
false随false的变化情况如下:
false
false
false
false
false
false
false
false
false
↘
极小值
↗
falsefalse. 由(*)式得false,代入上式得
false. 令false,
false,故false在false上单调递减.false,又false,.
即falsefalse.·················································································12分
方法二:falsefalse,································································8分
易得false,false,
所以false,得证false······················································12分
22.解:(1)false,······································································1分
当false时,false,false;false,false,此时false恒成立,则false不是函数false的极值点·······················································································3分
所以false···············································································4分
(2)false只有一个零点,显然是false,所以分为两种情况
第1种情况:false满足false,此时false·····················································6分
第2种情况:false无解,
令false,false;
①当false时,false,false单调递增false,故在false上存在false使得false;·························································································8分
②当false时,方程false显然无解;·······························································9分
③当false时,false解得false,当false时,false,false单调递减;当false时,false,false单调递增,则false,即false,所以false·································································································11分
综上所述:false················································································12分
同课章节目录
