沪教版五年级下册数学习题-6.5 图形与几何(面积的计算)(无答案)
文档属性
| 名称 | 沪教版五年级下册数学习题-6.5 图形与几何(面积的计算)(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 117.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 00:00:00 | ||
图片预览


文档简介
面积的计算(复习与提高)
班级
姓名
学号
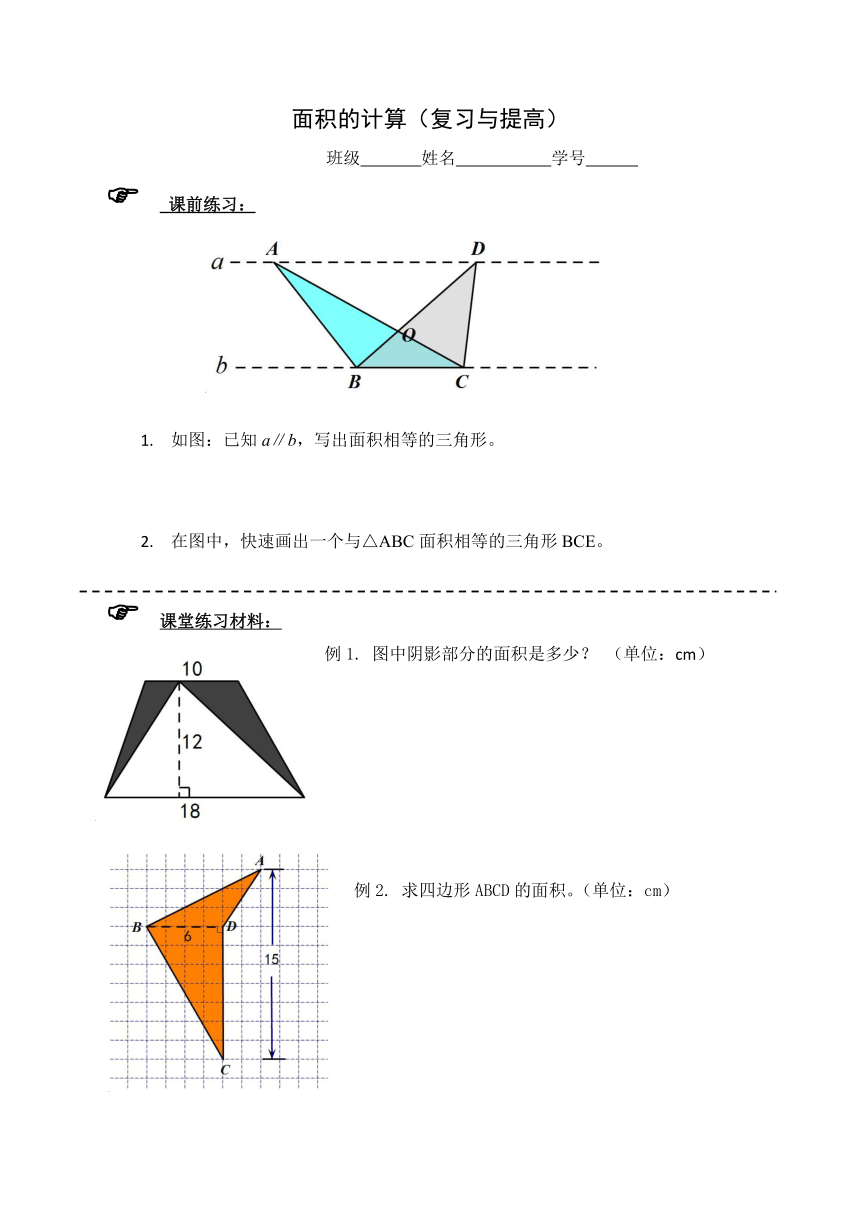
课前练习:
1.
如图:已知a∥b,写出面积相等的三角形。
2.
在图中,快速画出一个与△ABC面积相等的三角形BCE。
课堂练习材料:
例1.
图中阴影部分的面积是多少?
(单位:cm)
例2.
求四边形ABCD的面积。(单位:cm)
例3.
如图,△ABC和△DEF是完全相等的两个直角三角形。
已知AB=10cm,AD=3cm,EO=2cm。求四边形OEFC的面积。
例4.
下面组合图形中大小正方形的边长分别是13cm和9cm。
(
(
2
)图中
阴影
部分的面积是多少?
(
启发你想到很简洁的计算方法了吗?
)
)
(
(
1
)
算式“(
9+13
)×
9
÷
2
”,表示哪个图形的面积?
既可以表示
的面积,又可以表示
的面积。
)
例5.如图,长方形ABCD中,AB=12cm,BC=8cm,
三角形CEF的面积是28cm2,求梯形ABFD的面积。
面积的计算(复习与提高)
班级
姓名
学号
课后练习:
1.
图中AB、DC、FE互相平行,且AD∥BC,DF∥CE,这个图形的面积共是多少?
(单位:厘米)
2.
计算这个组合图形的面积(单位:分米)
3.
长方形ABCD的长12cm,宽5cm,三角形甲比乙的面积大15cm2,求CE的长度
比较下面三个图形,分别求出阴影部分的面积。(单位:厘米)
班级
姓名
学号
课前练习:
1.
如图:已知a∥b,写出面积相等的三角形。
2.
在图中,快速画出一个与△ABC面积相等的三角形BCE。
课堂练习材料:
例1.
图中阴影部分的面积是多少?
(单位:cm)
例2.
求四边形ABCD的面积。(单位:cm)
例3.
如图,△ABC和△DEF是完全相等的两个直角三角形。
已知AB=10cm,AD=3cm,EO=2cm。求四边形OEFC的面积。
例4.
下面组合图形中大小正方形的边长分别是13cm和9cm。
(
(
2
)图中
阴影
部分的面积是多少?
(
启发你想到很简洁的计算方法了吗?
)
)
(
(
1
)
算式“(
9+13
)×
9
÷
2
”,表示哪个图形的面积?
既可以表示
的面积,又可以表示
的面积。
)
例5.如图,长方形ABCD中,AB=12cm,BC=8cm,
三角形CEF的面积是28cm2,求梯形ABFD的面积。
面积的计算(复习与提高)
班级
姓名
学号
课后练习:
1.
图中AB、DC、FE互相平行,且AD∥BC,DF∥CE,这个图形的面积共是多少?
(单位:厘米)
2.
计算这个组合图形的面积(单位:分米)
3.
长方形ABCD的长12cm,宽5cm,三角形甲比乙的面积大15cm2,求CE的长度
比较下面三个图形,分别求出阴影部分的面积。(单位:厘米)
