江苏省淮安市2020-2021学年高一下学期期末调研测试数学试题 Word版含答案
文档属性
| 名称 | 江苏省淮安市2020-2021学年高一下学期期末调研测试数学试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 699.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-29 00:00:00 | ||
图片预览




文档简介
1027430010350500淮安市2020─2021学年度第二学期期末调研测试
高一数学试题
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若复数false,则z在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.每年的3月15日是“国际消费者权益日”,某地市场监管局在当天对某市场的20家肉制品店、100家粮食加工品店和15家乳制品店进行抽检,要用分层抽样的方法从中抽检27家,则粮食加工品店需要被抽检( )
A.20家 B.10家 C.15家 D.25家
3.在false中,角A,B,C所对的边分别是a,b,c,若false,则角A的大小为( )
A.false B.false C.false D.false
4.已知α为第二象限角,false,则false( )
A.false B.false C.false D.false
5.如图,在有五个正方形拼接而成的图形中,false( )
A.false B.false C.false D.false
6.已知m,n,l是不重合的三条直线,false,false,false是不重合的三个平面,则( )
A.若false,false,则false B.若false,false,false,则false
C.若false,false,false,则false D.若false,false,false,false,则false
7.古代将圆台称为“圆亭”,《九章算术》中“今有圆亭,下周三丈,上周二丈,高一丈,问积几何?”即一圆台形建筑物,下底周长3丈,上底周长2丈,高1丈,则它的体积为( )
A.false立方丈 B.false立方丈 C.false立方丈 D.false立方丈
8.已知点P是边长为1的正方形false的对角线false上的一点,则false的最小值为( )
A.false B.false C.false D.false
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.下列说法中正确的是( )
A.若false,false,则false
B.对于向量false,false,false,有false
C.向量false,false能作为所在平面内的一组基底
D.设false,false为非零向量,则“存在负数λ,使得false”是“false”的充分而不必要条件
10.某位同学连续抛掷质地均匀的骰子10次,向上的点数分别为1,2,2,2,3,3,3,4,5,5,则这10个数( )
A.众数为2和3 B.标准差为false C.平均数为3 D.第85百分位数为4.5
11.正六角星形是人们普遍知道的犹太人标志,凡是犹太人所到之处,都可看到这种标志.正六角星可由两个正三角形一上一下连锁组成(如图一).如图二所示的正六角星的中心为O,A,B,C是该正六角星的顶点,则( )
A.向量false,false的夹角为120°
B.若false,则false
C.false
D.若false,则false
12.如图,点M是棱长为1的正方体false的侧面false上的一个动点,则下列结论正确的是( )
A.二面角false的大小为45°
B.存在点false,使得异面直线false与false所成的角为30°
C.点M存在无数个位置满足false
D.点M存在无数个位置满足false面false
三、填空题:本题共4小题,每小题5分,共20分
13.若向量false,写出一个与向量false方向相反且共线的向量__________.
14.若一个水平放置的平面图形的斜二测直观图是等腰梯形,且false,false,则该平面图形的面积为__________.
15.已知false,false,false,false,则false__________.
16.粽子古称“角黍”,是中国传统的节庆食品之一,由粽叶包裹糯米等食材蒸制而成,因各地风俗不同,粽子的形状和味道也不同,某地流行的“五角粽子”,其形状可以看成所有棱长都相等的正四棱锥,现在需要在粽子内部放入一颗咸蛋黄,蛋黄的形状近似地看成球,则当这个蛋黄的体积最大时,正四棱锥的高与蛋黄半径的比值为__________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
设复数false,false,i为虚数单位).
(1)若false为实数,求m的值;
(2)若false,且false,求m的值.
18.(本小题满分12分)
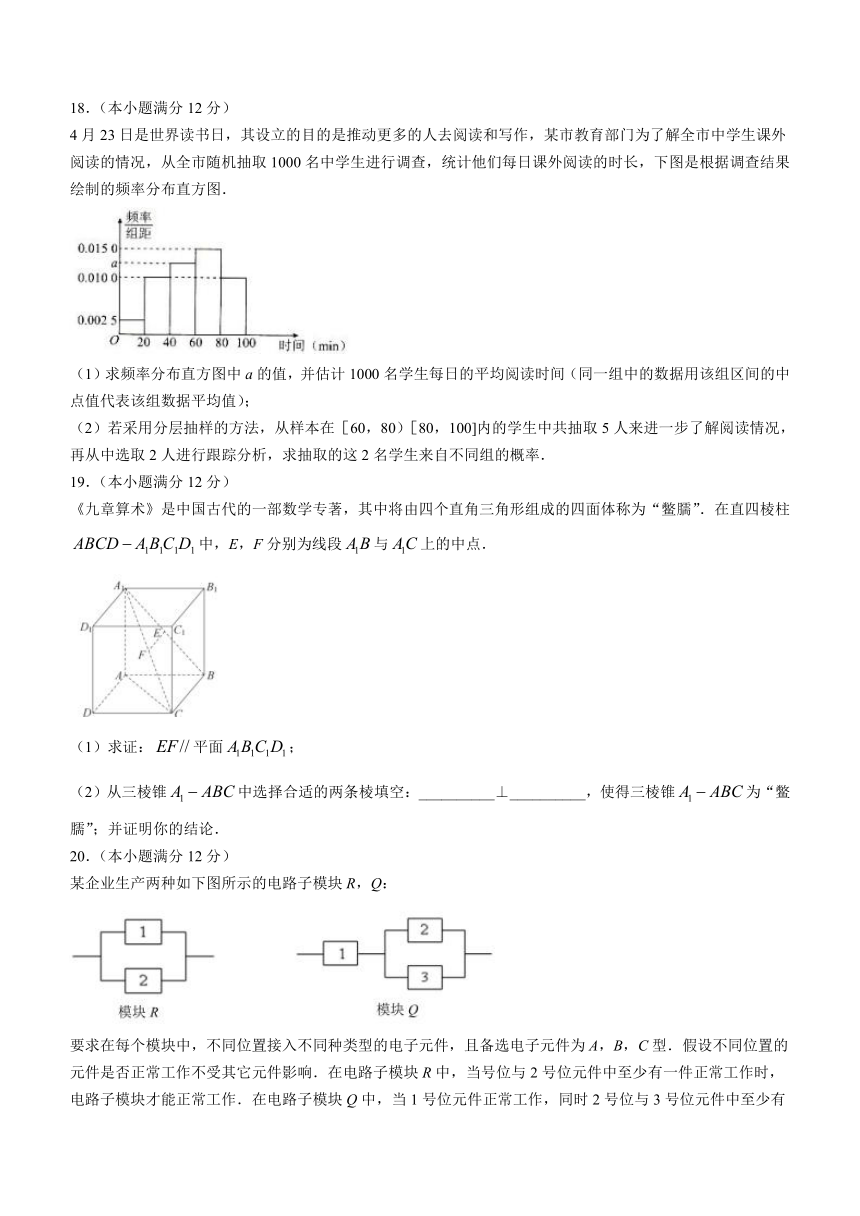
4月23日是世界读书日,其设立的目的是推动更多的人去阅读和写作,某市教育部门为了解全市中学生课外阅读的情况,从全市随机抽取1000名中学生进行调查,统计他们每日课外阅读的时长,下图是根据调查结果绘制的频率分布直方图.
(1)求频率分布直方图中a的值,并估计1000名学生每日的平均阅读时间(同一组中的数据用该组区间的中点值代表该组数据平均值);
(2)若采用分层抽样的方法,从样本在[60,80)[80,100]内的学生中共抽取5人来进一步了解阅读情况,再从中选取2人进行跟踪分析,求抽取的这2名学生来自不同组的概率.
19.(本小题满分12分)
《九章算术》是中国古代的一部数学专著,其中将由四个直角三角形组成的四面体称为“鳖臑”.在直四棱柱false中,E,F分别为线段false与false上的中点.
(1)求证:false平面false;
(2)从三棱锥false中选择合适的两条棱填空:__________⊥__________,使得三棱锥false为“鳖臑”;并证明你的结论.
20.(本小题满分12分)
某企业生产两种如下图所示的电路子模块R,Q:
要求在每个模块中,不同位置接入不同种类型的电子元件,且备选电子元件为A,B,C型.假设不同位置的元件是否正常工作不受其它元件影响.在电路子模块R中,当号位与2号位元件中至少有一件正常工作时,电路子模块才能正常工作.在电路子模块Q中,当1号位元件正常工作,同时2号位与3号位元件中至少有一件正常工作时,电路子模块才能正常工作.
(1)若备选电子元件A,B型正常工作的概率分别为0.9,0.8,依次接入位置1,2,求此时电路子模块R能正常工作的概率;
(2)若备选电子元件A,B,C型正常工作的概率分别为0.7,0.8,0.9,试问如何接入备选电子元件,电路子模块Q能正常工作的概率最大,并说明理由.
21.(本小题满分12分)
从①false;②false;③false这三个条件中选一个,补充到下面问题中,并完成解答.
已知false中,角A,B,C所对的边分别是a,b,c,且__________.
(1)求角A的大小;
(2)若false为锐角三角形,false,求false的周长的取值范围.
22.(本小题满分12分)
如图,在三棱锥false中,false,false,false,且false,false,false两两夹角都为false.
(1)若false,求三棱锥false的体积;
(2)若false,求三棱锥false的体积.
淮安市2020—2021学年度第二学期期末调研测试
高一数学试题
一、单项选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【答案】A
【解析】坐标为(1,1)
2.【答案】A
【解析】三种店的比例为20:100:15=4:20:23故抽20家粮食加工店.
3.【答案】D
【解析】由题意知false,则false.
4.【答案】B
【解析】false,false
5.【答案】C
【解析】false,false,false
6.【答案】C
【解析】A错误,还可以在平面false内.B错误,false,false可以互相垂直.D错误,false,false可以相交.
7.【答案】B
【解析】设上底半径为r,下底半径为R,false,false,false,false
false
8.【答案】C
【解析】如图
false,false
false
false,false,此时P与B重合.
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.【答案】CD
【解析】A:false不能为false;B:两向量方向未必相同.
10.【答案】AC
【解析】众数为2和3,平均数为false;
标准差false,
这组数按照从小到大排为1,2,2,2,3,3,3,4,5,5false,8.5非整数,则第85百分位数为第九个数5.
11.【答案】ABC
【解析】false由两个小正三角形,为false.
false
C:有平行四边形法则可知,false,false
则false
D:由平行四边形法则可知,若以false,false为基底分解,则系数和应该为复制,否则方向与false不一致,故错误.
12.【答案】A:这个二面角的大小即为false的二面角大小为45°
B:∵false平行false∴false为异面直线false与false所成角当M在线段false,移动时,M取false中点,
false最小,正弦值为false,错误.
C:当M在false上时,满足条件.∵false,false,false∴false平面false
∵false平面false∴false|
false,false平面false,false平面false
∴false平面false,
∵false,false平面false,false平面false
∴false平面false
∵false
∴平面false平面false
当M在false时,false平面false
∴false平面false
三、填空题:本题共4小题,每小题5分,共20分
13.【答案】(1,2)
【解析】false,false时,方向相反且共线,所以false.
14.【答案】false
【解析】作false,false,因为false,false,false
所以false,false.因此false.
又根据斜二测画法的特征可得,在原图中
false,false,即原图为直角梯形,且高为直观图中false的2倍,
所以该平面图形的面积为
false.
15.【答案】false
【解析】因为false,false,所以false.
false.
false,因为false,所以false.
16.【答案】false
【解析】设正四棱锥的棱长均为false,球的体积要达到最大,则需要球与四棱锥的五个面都相切.
正四棱锥的高false,设球半径为r,四棱锥的面积false,
false,
false
false,false,所以false.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.【解析】(1)由于false,
所以false,解得false;
(2)由于false,所以false,解得false.
18.【解析】(1)由false可得false;
这1000名学生每日的平均阅读时间,false分钟;
(2)由于false,因此,[60,80)抽取了3人a,b,c,false抽取了2人d,e,
则再从中抽取2人共有false10种不同的抽取方法,
抽取的2人来自不同组共有6种可能,因此抽取的2人来自不同组的概率为false.
19.【解析】(1)证明:在直四棱柱false中,因为E,F分别为false边false与false的中点,
所以false,又因为false,所以false,因为false平面false,false平面false
所以false平面false;
(2)若false,则三棱锥false为“鳖臑”;且false为直角三角形;证明:在直四棱柱
false中,false平面false,所以false,false,所以false,false均为直角三角形;因为false,false,false,false,false平面false,所以false平面false;
又因为false平面false,所以false,所以false为直角三角形.
因此,三棱锥false的四个面均为直角三角形,三棱锥false为“鳖儒”.
20.【解析】(1)假设事件A,B,C分别表示电子元件A,B,C正常工作,电路子模块R不能正常工作的概率为false,由于事件A,B互相独立,所以false,
因此电路子模块R能正常工作的概率为false
(2)由于当1号位元件正常工作,同时2号位与3号位元件中至少有一件正常工作时,电路子模块Q才能正常工作,因此①若1号位元件为电子元件A,则电路子模块Q正常工作的概率为
false;
②若1号位元件为电子元件B,则电路子模块Q正常工作的概率为
false;
③若1号位元件为电子元件c,则电路子模块Q正常工作的概率为
false;
因此,1号位接入正常工作概率最大的元件C时,电路子模块Q正常工作的概率最大.
21.【解析】(1)若选①,在false中,由正弦定理得:false,
因为false,A,B,false,所以false且false,因此false,false;
若选②,在false中,由余弦定理得.false,
所以false,因为false,
因此false,且false,故false;
若选③,在false中,false,且false
由正弦定理得:false,故false,false;
(2)因为false为锐角三角形,所以false,false,因此false
由正弦定理得:false,
因为false,false,
所以false的周长为false,
false,false
由于false,所以false的周长取值范围为false.
22.【解析】(1)因为false,false,false,false,false平面false
所以false平面false,因此false,
(2)解法一,在线段false上取点D,使得false,连接false,false,
因为false,false,false,
由于余弦定理可得:false,所以false
同理可得:false,又因为false,false,false平面false,
所以false平面false,在等腰三角形false中,
因为false,false,
所以false,所以三棱锥false的体积为false.
由于false,因此false.
解法二:过点B作面false的垂线,垂足为H,
过点B作false的垂线,垂足为M,
连接false,false,false,因为false,false,false,
由于余弦定理可得:false,所以false,
false,false,false,
所以false与false全等,故false,
又因为false,所以直角三角形false与false全等,
false,因为false,false,false,false平面false,
false,所以false平面false.
又因为false平面false,所以false﹔
同理可得:false,在直角三角形false,false中,
因为false,false,所以false与false全等,
false,点H在false的平分线上,
因为false为直角三角形,false,false,
false,所以false,
因此false,false.
高一数学试题
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若复数false,则z在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.每年的3月15日是“国际消费者权益日”,某地市场监管局在当天对某市场的20家肉制品店、100家粮食加工品店和15家乳制品店进行抽检,要用分层抽样的方法从中抽检27家,则粮食加工品店需要被抽检( )
A.20家 B.10家 C.15家 D.25家
3.在false中,角A,B,C所对的边分别是a,b,c,若false,则角A的大小为( )
A.false B.false C.false D.false
4.已知α为第二象限角,false,则false( )
A.false B.false C.false D.false
5.如图,在有五个正方形拼接而成的图形中,false( )
A.false B.false C.false D.false
6.已知m,n,l是不重合的三条直线,false,false,false是不重合的三个平面,则( )
A.若false,false,则false B.若false,false,false,则false
C.若false,false,false,则false D.若false,false,false,false,则false
7.古代将圆台称为“圆亭”,《九章算术》中“今有圆亭,下周三丈,上周二丈,高一丈,问积几何?”即一圆台形建筑物,下底周长3丈,上底周长2丈,高1丈,则它的体积为( )
A.false立方丈 B.false立方丈 C.false立方丈 D.false立方丈
8.已知点P是边长为1的正方形false的对角线false上的一点,则false的最小值为( )
A.false B.false C.false D.false
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.下列说法中正确的是( )
A.若false,false,则false
B.对于向量false,false,false,有false
C.向量false,false能作为所在平面内的一组基底
D.设false,false为非零向量,则“存在负数λ,使得false”是“false”的充分而不必要条件
10.某位同学连续抛掷质地均匀的骰子10次,向上的点数分别为1,2,2,2,3,3,3,4,5,5,则这10个数( )
A.众数为2和3 B.标准差为false C.平均数为3 D.第85百分位数为4.5
11.正六角星形是人们普遍知道的犹太人标志,凡是犹太人所到之处,都可看到这种标志.正六角星可由两个正三角形一上一下连锁组成(如图一).如图二所示的正六角星的中心为O,A,B,C是该正六角星的顶点,则( )
A.向量false,false的夹角为120°
B.若false,则false
C.false
D.若false,则false
12.如图,点M是棱长为1的正方体false的侧面false上的一个动点,则下列结论正确的是( )
A.二面角false的大小为45°
B.存在点false,使得异面直线false与false所成的角为30°
C.点M存在无数个位置满足false
D.点M存在无数个位置满足false面false
三、填空题:本题共4小题,每小题5分,共20分
13.若向量false,写出一个与向量false方向相反且共线的向量__________.
14.若一个水平放置的平面图形的斜二测直观图是等腰梯形,且false,false,则该平面图形的面积为__________.
15.已知false,false,false,false,则false__________.
16.粽子古称“角黍”,是中国传统的节庆食品之一,由粽叶包裹糯米等食材蒸制而成,因各地风俗不同,粽子的形状和味道也不同,某地流行的“五角粽子”,其形状可以看成所有棱长都相等的正四棱锥,现在需要在粽子内部放入一颗咸蛋黄,蛋黄的形状近似地看成球,则当这个蛋黄的体积最大时,正四棱锥的高与蛋黄半径的比值为__________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
设复数false,false,i为虚数单位).
(1)若false为实数,求m的值;
(2)若false,且false,求m的值.
18.(本小题满分12分)
4月23日是世界读书日,其设立的目的是推动更多的人去阅读和写作,某市教育部门为了解全市中学生课外阅读的情况,从全市随机抽取1000名中学生进行调查,统计他们每日课外阅读的时长,下图是根据调查结果绘制的频率分布直方图.
(1)求频率分布直方图中a的值,并估计1000名学生每日的平均阅读时间(同一组中的数据用该组区间的中点值代表该组数据平均值);
(2)若采用分层抽样的方法,从样本在[60,80)[80,100]内的学生中共抽取5人来进一步了解阅读情况,再从中选取2人进行跟踪分析,求抽取的这2名学生来自不同组的概率.
19.(本小题满分12分)
《九章算术》是中国古代的一部数学专著,其中将由四个直角三角形组成的四面体称为“鳖臑”.在直四棱柱false中,E,F分别为线段false与false上的中点.
(1)求证:false平面false;
(2)从三棱锥false中选择合适的两条棱填空:__________⊥__________,使得三棱锥false为“鳖臑”;并证明你的结论.
20.(本小题满分12分)
某企业生产两种如下图所示的电路子模块R,Q:
要求在每个模块中,不同位置接入不同种类型的电子元件,且备选电子元件为A,B,C型.假设不同位置的元件是否正常工作不受其它元件影响.在电路子模块R中,当号位与2号位元件中至少有一件正常工作时,电路子模块才能正常工作.在电路子模块Q中,当1号位元件正常工作,同时2号位与3号位元件中至少有一件正常工作时,电路子模块才能正常工作.
(1)若备选电子元件A,B型正常工作的概率分别为0.9,0.8,依次接入位置1,2,求此时电路子模块R能正常工作的概率;
(2)若备选电子元件A,B,C型正常工作的概率分别为0.7,0.8,0.9,试问如何接入备选电子元件,电路子模块Q能正常工作的概率最大,并说明理由.
21.(本小题满分12分)
从①false;②false;③false这三个条件中选一个,补充到下面问题中,并完成解答.
已知false中,角A,B,C所对的边分别是a,b,c,且__________.
(1)求角A的大小;
(2)若false为锐角三角形,false,求false的周长的取值范围.
22.(本小题满分12分)
如图,在三棱锥false中,false,false,false,且false,false,false两两夹角都为false.
(1)若false,求三棱锥false的体积;
(2)若false,求三棱锥false的体积.
淮安市2020—2021学年度第二学期期末调研测试
高一数学试题
一、单项选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【答案】A
【解析】坐标为(1,1)
2.【答案】A
【解析】三种店的比例为20:100:15=4:20:23故抽20家粮食加工店.
3.【答案】D
【解析】由题意知false,则false.
4.【答案】B
【解析】false,false
5.【答案】C
【解析】false,false,false
6.【答案】C
【解析】A错误,还可以在平面false内.B错误,false,false可以互相垂直.D错误,false,false可以相交.
7.【答案】B
【解析】设上底半径为r,下底半径为R,false,false,false,false
false
8.【答案】C
【解析】如图
false,false
false
false,false,此时P与B重合.
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.【答案】CD
【解析】A:false不能为false;B:两向量方向未必相同.
10.【答案】AC
【解析】众数为2和3,平均数为false;
标准差false,
这组数按照从小到大排为1,2,2,2,3,3,3,4,5,5false,8.5非整数,则第85百分位数为第九个数5.
11.【答案】ABC
【解析】false由两个小正三角形,为false.
false
C:有平行四边形法则可知,false,false
则false
D:由平行四边形法则可知,若以false,false为基底分解,则系数和应该为复制,否则方向与false不一致,故错误.
12.【答案】A:这个二面角的大小即为false的二面角大小为45°
B:∵false平行false∴false为异面直线false与false所成角当M在线段false,移动时,M取false中点,
false最小,正弦值为false,错误.
C:当M在false上时,满足条件.∵false,false,false∴false平面false
∵false平面false∴false|
false,false平面false,false平面false
∴false平面false,
∵false,false平面false,false平面false
∴false平面false
∵false
∴平面false平面false
当M在false时,false平面false
∴false平面false
三、填空题:本题共4小题,每小题5分,共20分
13.【答案】(1,2)
【解析】false,false时,方向相反且共线,所以false.
14.【答案】false
【解析】作false,false,因为false,false,false
所以false,false.因此false.
又根据斜二测画法的特征可得,在原图中
false,false,即原图为直角梯形,且高为直观图中false的2倍,
所以该平面图形的面积为
false.
15.【答案】false
【解析】因为false,false,所以false.
false.
false,因为false,所以false.
16.【答案】false
【解析】设正四棱锥的棱长均为false,球的体积要达到最大,则需要球与四棱锥的五个面都相切.
正四棱锥的高false,设球半径为r,四棱锥的面积false,
false,
false
false,false,所以false.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.【解析】(1)由于false,
所以false,解得false;
(2)由于false,所以false,解得false.
18.【解析】(1)由false可得false;
这1000名学生每日的平均阅读时间,false分钟;
(2)由于false,因此,[60,80)抽取了3人a,b,c,false抽取了2人d,e,
则再从中抽取2人共有false10种不同的抽取方法,
抽取的2人来自不同组共有6种可能,因此抽取的2人来自不同组的概率为false.
19.【解析】(1)证明:在直四棱柱false中,因为E,F分别为false边false与false的中点,
所以false,又因为false,所以false,因为false平面false,false平面false
所以false平面false;
(2)若false,则三棱锥false为“鳖臑”;且false为直角三角形;证明:在直四棱柱
false中,false平面false,所以false,false,所以false,false均为直角三角形;因为false,false,false,false,false平面false,所以false平面false;
又因为false平面false,所以false,所以false为直角三角形.
因此,三棱锥false的四个面均为直角三角形,三棱锥false为“鳖儒”.
20.【解析】(1)假设事件A,B,C分别表示电子元件A,B,C正常工作,电路子模块R不能正常工作的概率为false,由于事件A,B互相独立,所以false,
因此电路子模块R能正常工作的概率为false
(2)由于当1号位元件正常工作,同时2号位与3号位元件中至少有一件正常工作时,电路子模块Q才能正常工作,因此①若1号位元件为电子元件A,则电路子模块Q正常工作的概率为
false;
②若1号位元件为电子元件B,则电路子模块Q正常工作的概率为
false;
③若1号位元件为电子元件c,则电路子模块Q正常工作的概率为
false;
因此,1号位接入正常工作概率最大的元件C时,电路子模块Q正常工作的概率最大.
21.【解析】(1)若选①,在false中,由正弦定理得:false,
因为false,A,B,false,所以false且false,因此false,false;
若选②,在false中,由余弦定理得.false,
所以false,因为false,
因此false,且false,故false;
若选③,在false中,false,且false
由正弦定理得:false,故false,false;
(2)因为false为锐角三角形,所以false,false,因此false
由正弦定理得:false,
因为false,false,
所以false的周长为false,
false,false
由于false,所以false的周长取值范围为false.
22.【解析】(1)因为false,false,false,false,false平面false
所以false平面false,因此false,
(2)解法一,在线段false上取点D,使得false,连接false,false,
因为false,false,false,
由于余弦定理可得:false,所以false
同理可得:false,又因为false,false,false平面false,
所以false平面false,在等腰三角形false中,
因为false,false,
所以false,所以三棱锥false的体积为false.
由于false,因此false.
解法二:过点B作面false的垂线,垂足为H,
过点B作false的垂线,垂足为M,
连接false,false,false,因为false,false,false,
由于余弦定理可得:false,所以false,
false,false,false,
所以false与false全等,故false,
又因为false,所以直角三角形false与false全等,
false,因为false,false,false,false平面false,
false,所以false平面false.
又因为false平面false,所以false﹔
同理可得:false,在直角三角形false,false中,
因为false,false,所以false与false全等,
false,点H在false的平分线上,
因为false为直角三角形,false,false,
false,所以false,
因此false,false.
同课章节目录
