13.2.5 边边边练习题-2021——2022学年华东师大版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 13.2.5 边边边练习题-2021——2022学年华东师大版八年级数学上册(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 00:00:00 | ||
图片预览



文档简介
13.2.5 边边边
【基础练习】
知识点
1 “角角角”不能判定三角形全等
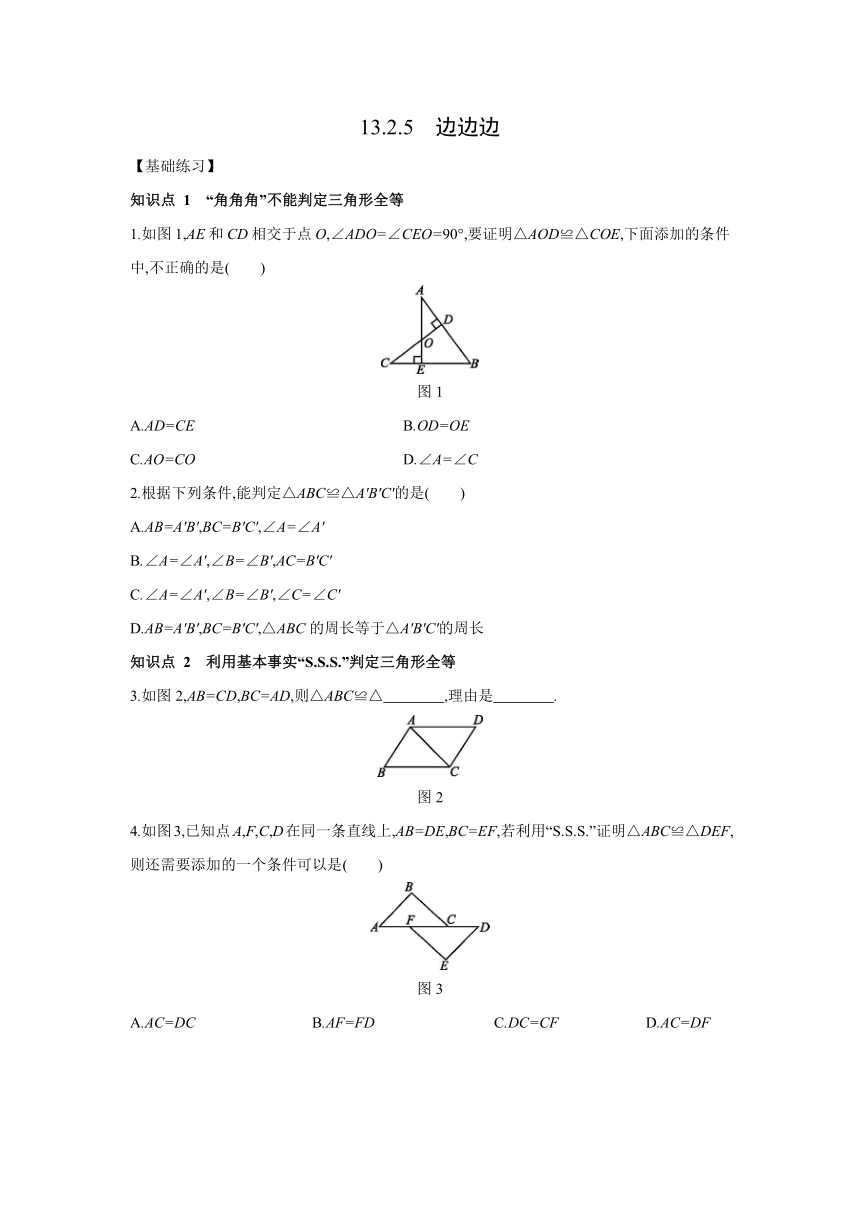
1.如图1,AE和CD相交于点O,∠ADO=∠CEO=90°,要证明△AOD≌△COE,下面添加的条件中,不正确的是( )
图1
A.AD=CE
B.OD=OE
C.AO=CO
D.∠A=∠C
2.根据下列条件,能判定△ABC≌△A'B'C'的是( )
A.AB=A'B',BC=B'C',∠A=∠A'
B.∠A=∠A',∠B=∠B',AC=B'C'
C.∠A=∠A',∠B=∠B',∠C=∠C'
D.AB=A'B',BC=B'C',△ABC的周长等于△A'B'C'的周长
知识点
2 利用基本事实“S.S.S.”判定三角形全等
3.如图2,AB=CD,BC=AD,则△ABC≌△ ,理由是 .?
图2
4.如图3,已知点A,F,C,D在同一条直线上,AB=DE,BC=EF,若利用“S.S.S.”证明△ABC≌△DEF,则还需要添加的一个条件可以是( )
图3
A.AC=DC
B.AF=FD
C.DC=CF
D.AC=DF
5.[2019·西藏]
如图4,点E,C在线段BF上,BE=CF,AB=DE,AC=DF.
求证:∠ABC=∠DEF.
图4
知识点
3 基本事实“S.S.S.”的简单应用
6.工人师傅常用角尺平分一个任意角,做法如下:如图5,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC.由此作法便可得△NOC≌△MOC,其依据是( )
图5
A.S.S.S.
B.S.A.S.
C.A.S.A.
D.A.A.S.
7.如图6,有两根长12
m的绳子,一端系在旗杆上的同一位置,另一端分别固定在地面上的两个木桩上(绳结处的误差忽略不计),现在只有一把卷尺,如何来检验旗杆是否垂直于地面?说明理由.
图6
8.如图7,点B,F,C,E在直线l上(点F,C之间不能直接测量),点A,D在直线l异侧,测得AB=DE,AC=DF,BF=EC.图中线段AB与DE平行吗?请说明理由.
图7
【能力提升】
9.如图8,CA=CB,AD=BD,M,N分别是CA,CB的中点.若DM=5
cm,则DN等于( )
图8
A.3
cm
B.4
cm
C.5
cm
D.6
cm
10.如图9,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
图9
A.1个
B.2个
C.3个
D.4个
11.[2019·桂林]
如图10,AB=AD,BC=DC,点E在AC上.
求证:(1)AC平分∠BAD;
(2)BE=DE.
图10
12.雨伞的中截面如图11所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,则雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
图11
13.如图12所示,D是BC上一点,AB=AD,BC=DE,AC=AE.求证:∠CDE=∠BAD.
图12
14.如图13,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从点D出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当其中一个点到达终点时,其余两点也随之停止移动.
(1)求证:AD∥BC;
(2)在移动过程中,小明发现当点G的移动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的移动速度取哪些值时,有△DEG与△BFG全等的情况出现.
图13
答案
1.D [解析]
在△AOD与△COE中,∠ADO=∠CEO=90°,∠AOD=∠COE(对顶角相等).
A项,若添加AD=CE,根据全等三角形的判定定理A.A.S.可以判定△AOD≌△COE,故本选项不符合题意.
B项,若添加OD=OE,根据判定三角形全等的基本事实A.S.A.可以判定△AOD≌△COE,故本选项不符合题意.
C项,若添加AO=CO,根据全等三角形的判定定理A.A.S.可以判定△AOD≌△COE,故本选项不符合题意.
D项,若添加∠A=∠C,在△AOD与△COE中,没有对应边相等,不能判定它们全等,故本选项符合题意.故选D.
2.D
3.CDA S.S.S. [解析]
在△ABC和△CDA中,∵AB=CD,BC=DA,AC=CA,
∴△ABC≌△CDA(S.S.S.).故答案为CDA,S.S.S..
4.D [解析]
利用“S.S.S.”证明△ABC≌△DEF,还需要添加的一个条件可以是AC=DF.理由如下:
在△ABC和△DEF中,
∵AB=DE,BC=EF,AC=DF,
∴△ABC≌△DEF(S.S.S.).故选D.
5.证明:∵BE=CF,∴BE+EC=CF+EC,
即BC=EF.
在△ABC与△DEF中,
∵AB=DE,BC=EF,AC=DF,
∴△ABC≌△DEF(S.S.S.),∴∠ABC=∠DEF.
6.A [解析]
在△NOC和△MOC中,
∵ON=OM,CO=CO,NC=MC,
∴△NOC≌△MOC(S.S.S.),
∴∠BOC=∠AOC.
故选A.
7.解:用卷尺测量出BD,CD的长度,看它们是否相等.若BD=CD,则AD⊥BC.
理由:在△ABD和△ACD中,
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(S.S.S.),
∴∠ADB=∠ADC.
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC.
8.解:图中线段AB与DE平行.
理由:∵BF=EC,
∴BF+FC=FC+EC,
即BC=EF.
在△ABC和△DEF中,
∵AB=DE,AC=DF,BC=EF,
∴△ABC≌△DEF(S.S.S.),
∴∠ABC=∠DEF,
∴AB∥DE.
9.C [解析]
连结CD.
在△ADC与△BDC中,
∵CA=CB,AD=BD,CD=CD,
∴△ADC≌△BDC(S.S.S.),∴∠A=∠B.
∵M,N分别是CA,CB的中点,
∴AM=BN.
在△ADM与△BDN中,
∵AM=BN,∠A=∠B,AD=BD,
∴△ADM≌△BDN(S.A.S.),
∴DN=DM=5
cm.
10.C [解析]
要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位,故点P的位置可以是P1,P3,P4,共3个.故选C.
11.证明:(1)在△ABC与△ADC中,
∵AB=AD,AC=AC,BC=DC,
∴△ABC≌△ADC(S.S.S.),
∴∠BAC=∠DAC,∴AC平分∠BAD.
(2)由(1)知∠BAE=∠DAE.
在△BAE与△DAE中,
∵AB=AD,∠BAE=∠DAE,AE=AE,
∴△BAE≌△DAE(S.A.S.),
∴BE=DE.
12.解:∠BAD=∠CAD.
理由:∵AB=AC,AE=AB,AF=AC,
∴AE=AF.
在△AEO和△AFO中,
∵AE=AF,AO=AO,OE=OF,
∴△AEO≌△AFO(S.S.S.),
∴∠BAD=∠CAD.
13.证明:在△ABC与△ADE中,
∵AB=AD,BC=DE,AC=AE,
∴△ABC≌△ADE(S.S.S.),
∴∠BAC=∠DAE,∠C=∠E,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
在△AEF和△DCF中,
∵∠E=∠C,∠AFE=∠DFC,
∴∠CAE=∠CDE,∴∠CDE=∠BAD.
14.解:(1)证明:在△ABD和△CDB中,
∵AD=CB,AB=CD,BD=DB,
∴△ABD≌△CDB(S.S.S.),
∴∠ADB=∠CBD,∴AD∥BC.
(2)设移动时间为t秒,点G的移动速度为每秒v个单位.
当0则DE=BF,DG=BG,
∴
∴∴v=3;
若△DEG≌△BGF,则DE=BG,DG=BF,
∴
∴(不合题意,舍去);
当则DE=BF,DG=BG,
∴∴
∴v=1.5;
若△DEG≌△BGF,则DE=BG,DG=BF,
∴∴
∴v=1.
综上,当点G的移动速度为每秒1.5个单位或3个单位或1个单位时,有△DEG与△BFG全等的情况出现.
【基础练习】
知识点
1 “角角角”不能判定三角形全等
1.如图1,AE和CD相交于点O,∠ADO=∠CEO=90°,要证明△AOD≌△COE,下面添加的条件中,不正确的是( )
图1
A.AD=CE
B.OD=OE
C.AO=CO
D.∠A=∠C
2.根据下列条件,能判定△ABC≌△A'B'C'的是( )
A.AB=A'B',BC=B'C',∠A=∠A'
B.∠A=∠A',∠B=∠B',AC=B'C'
C.∠A=∠A',∠B=∠B',∠C=∠C'
D.AB=A'B',BC=B'C',△ABC的周长等于△A'B'C'的周长
知识点
2 利用基本事实“S.S.S.”判定三角形全等
3.如图2,AB=CD,BC=AD,则△ABC≌△ ,理由是 .?
图2
4.如图3,已知点A,F,C,D在同一条直线上,AB=DE,BC=EF,若利用“S.S.S.”证明△ABC≌△DEF,则还需要添加的一个条件可以是( )
图3
A.AC=DC
B.AF=FD
C.DC=CF
D.AC=DF
5.[2019·西藏]
如图4,点E,C在线段BF上,BE=CF,AB=DE,AC=DF.
求证:∠ABC=∠DEF.
图4
知识点
3 基本事实“S.S.S.”的简单应用
6.工人师傅常用角尺平分一个任意角,做法如下:如图5,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC.由此作法便可得△NOC≌△MOC,其依据是( )
图5
A.S.S.S.
B.S.A.S.
C.A.S.A.
D.A.A.S.
7.如图6,有两根长12
m的绳子,一端系在旗杆上的同一位置,另一端分别固定在地面上的两个木桩上(绳结处的误差忽略不计),现在只有一把卷尺,如何来检验旗杆是否垂直于地面?说明理由.
图6
8.如图7,点B,F,C,E在直线l上(点F,C之间不能直接测量),点A,D在直线l异侧,测得AB=DE,AC=DF,BF=EC.图中线段AB与DE平行吗?请说明理由.
图7
【能力提升】
9.如图8,CA=CB,AD=BD,M,N分别是CA,CB的中点.若DM=5
cm,则DN等于( )
图8
A.3
cm
B.4
cm
C.5
cm
D.6
cm
10.如图9,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
图9
A.1个
B.2个
C.3个
D.4个
11.[2019·桂林]
如图10,AB=AD,BC=DC,点E在AC上.
求证:(1)AC平分∠BAD;
(2)BE=DE.
图10
12.雨伞的中截面如图11所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O沿AD滑动时,雨伞开闭,则雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
图11
13.如图12所示,D是BC上一点,AB=AD,BC=DE,AC=AE.求证:∠CDE=∠BAD.
图12
14.如图13,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从点D出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当其中一个点到达终点时,其余两点也随之停止移动.
(1)求证:AD∥BC;
(2)在移动过程中,小明发现当点G的移动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的移动速度取哪些值时,有△DEG与△BFG全等的情况出现.
图13
答案
1.D [解析]
在△AOD与△COE中,∠ADO=∠CEO=90°,∠AOD=∠COE(对顶角相等).
A项,若添加AD=CE,根据全等三角形的判定定理A.A.S.可以判定△AOD≌△COE,故本选项不符合题意.
B项,若添加OD=OE,根据判定三角形全等的基本事实A.S.A.可以判定△AOD≌△COE,故本选项不符合题意.
C项,若添加AO=CO,根据全等三角形的判定定理A.A.S.可以判定△AOD≌△COE,故本选项不符合题意.
D项,若添加∠A=∠C,在△AOD与△COE中,没有对应边相等,不能判定它们全等,故本选项符合题意.故选D.
2.D
3.CDA S.S.S. [解析]
在△ABC和△CDA中,∵AB=CD,BC=DA,AC=CA,
∴△ABC≌△CDA(S.S.S.).故答案为CDA,S.S.S..
4.D [解析]
利用“S.S.S.”证明△ABC≌△DEF,还需要添加的一个条件可以是AC=DF.理由如下:
在△ABC和△DEF中,
∵AB=DE,BC=EF,AC=DF,
∴△ABC≌△DEF(S.S.S.).故选D.
5.证明:∵BE=CF,∴BE+EC=CF+EC,
即BC=EF.
在△ABC与△DEF中,
∵AB=DE,BC=EF,AC=DF,
∴△ABC≌△DEF(S.S.S.),∴∠ABC=∠DEF.
6.A [解析]
在△NOC和△MOC中,
∵ON=OM,CO=CO,NC=MC,
∴△NOC≌△MOC(S.S.S.),
∴∠BOC=∠AOC.
故选A.
7.解:用卷尺测量出BD,CD的长度,看它们是否相等.若BD=CD,则AD⊥BC.
理由:在△ABD和△ACD中,
∵AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD(S.S.S.),
∴∠ADB=∠ADC.
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC.
8.解:图中线段AB与DE平行.
理由:∵BF=EC,
∴BF+FC=FC+EC,
即BC=EF.
在△ABC和△DEF中,
∵AB=DE,AC=DF,BC=EF,
∴△ABC≌△DEF(S.S.S.),
∴∠ABC=∠DEF,
∴AB∥DE.
9.C [解析]
连结CD.
在△ADC与△BDC中,
∵CA=CB,AD=BD,CD=CD,
∴△ADC≌△BDC(S.S.S.),∴∠A=∠B.
∵M,N分别是CA,CB的中点,
∴AM=BN.
在△ADM与△BDN中,
∵AM=BN,∠A=∠B,AD=BD,
∴△ADM≌△BDN(S.A.S.),
∴DN=DM=5
cm.
10.C [解析]
要使△ABP与△ABC全等,点P到AB的距离应该等于点C到AB的距离,即3个单位,故点P的位置可以是P1,P3,P4,共3个.故选C.
11.证明:(1)在△ABC与△ADC中,
∵AB=AD,AC=AC,BC=DC,
∴△ABC≌△ADC(S.S.S.),
∴∠BAC=∠DAC,∴AC平分∠BAD.
(2)由(1)知∠BAE=∠DAE.
在△BAE与△DAE中,
∵AB=AD,∠BAE=∠DAE,AE=AE,
∴△BAE≌△DAE(S.A.S.),
∴BE=DE.
12.解:∠BAD=∠CAD.
理由:∵AB=AC,AE=AB,AF=AC,
∴AE=AF.
在△AEO和△AFO中,
∵AE=AF,AO=AO,OE=OF,
∴△AEO≌△AFO(S.S.S.),
∴∠BAD=∠CAD.
13.证明:在△ABC与△ADE中,
∵AB=AD,BC=DE,AC=AE,
∴△ABC≌△ADE(S.S.S.),
∴∠BAC=∠DAE,∠C=∠E,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
在△AEF和△DCF中,
∵∠E=∠C,∠AFE=∠DFC,
∴∠CAE=∠CDE,∴∠CDE=∠BAD.
14.解:(1)证明:在△ABD和△CDB中,
∵AD=CB,AB=CD,BD=DB,
∴△ABD≌△CDB(S.S.S.),
∴∠ADB=∠CBD,∴AD∥BC.
(2)设移动时间为t秒,点G的移动速度为每秒v个单位.
当0
∴
∴∴v=3;
若△DEG≌△BGF,则DE=BG,DG=BF,
∴
∴(不合题意,舍去);
当
∴∴
∴v=1.5;
若△DEG≌△BGF,则DE=BG,DG=BF,
∴∴
∴v=1.
综上,当点G的移动速度为每秒1.5个单位或3个单位或1个单位时,有△DEG与△BFG全等的情况出现.
