13.2.6斜边直角边练习题 -2021——2022学年华东师大版八年级数学上册(Word版含答案)
文档属性
| 名称 | 13.2.6斜边直角边练习题 -2021——2022学年华东师大版八年级数学上册(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 139.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 00:00:00 | ||
图片预览



文档简介
13.2.6 斜边直角边
【基础练习】
知识点
1 “H.L.”定理
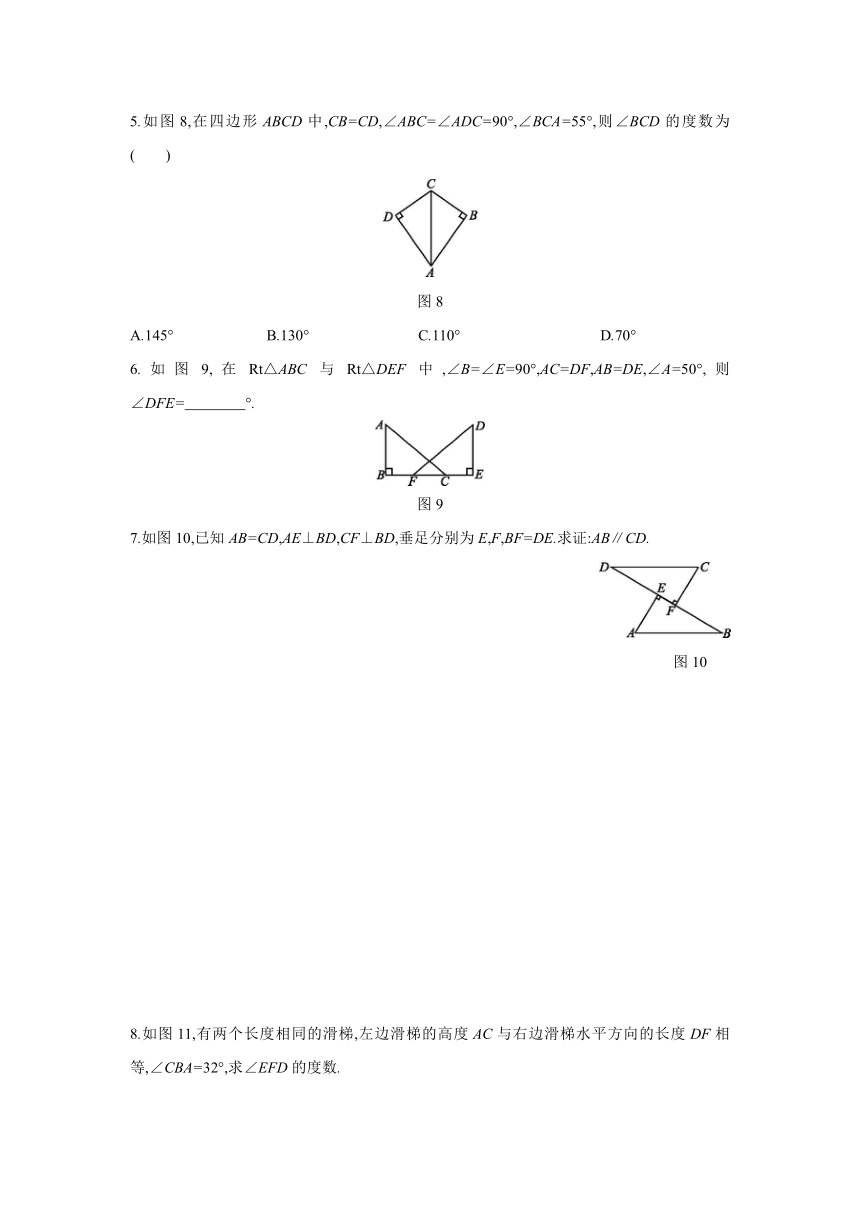
1.如图4,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,公共边AO=
,则Rt△ADO≌Rt△ ,理由是 .?
图4
2.如图5,能用“H.L.”判定Rt△ABC和Rt△A'B'C'全等的条件是( )
图5
A.AC=A'C',BC=B'C'
B.∠A=∠A',AB=A'B'
C.AC=A'C',AB=A'B'
D.∠B=∠B',BC=B'C'
3.如图6,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件: ,从而可以根据“H.L.”判定Rt△EAB≌Rt△BCD.?
图6
4.如图7,已知AC⊥BC,BD⊥AD,AC与BD交于点O,AC=BD.求证:△ABC≌△BAD.
图7
知识点
2 “H.L.”定理的应用
5.如图8,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BCA=55°,则∠BCD的度数为( )
图8
A.145°
B.130°
C.110°
D.70°
6.如图9,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,∠A=50°,则∠DFE= °.?
图9
7.如图10,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE.求证:AB∥CD.
图10
8.如图11,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,∠CBA=32°,求∠EFD的度数.
图11
【能力提升】
9.[2019·哈尔滨呼兰区期中]
如图12,在△ABC中,CD⊥AB于点D,E为CD上一点,EF⊥AC于点F,连结AE.若ED=EF,∠ECF=58°,则∠DAE的度数为( )
图12
A.32°
B.18°
C.16°
D.29°
10.如图13,D为Rt△ABC中斜边BC上的一点,且BD=AB,过点D作BC的垂线,交AC于点E.若AE=12
cm,则DE的长为 cm.?
图13
11.如图14所示,在Rt△ABC中,∠C=90°,AC=10,BC=5,一条线段PQ=AB,点P,Q分别在AC和过点A且垂直于AC的射线AX上运动,当AP= 时,△ABC与△APQ全等.?
图14
12.如图15,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
(1)图中有几对全等的三角形?请一一列出;
(2)选择一对你认为全等的三角形进行证明.
图15
13.已知:如图16所示,BE⊥CD于点E,BE=DE,A为BE上一点,且BC=DA,DA的延长线交BC于点F.
求证:(1)△BEC≌△DEA;
(2)DF⊥BC.
图16
14.如图17,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)若点B,C在DE的同侧(如图①),且AD=CE,求证:AB⊥AC.
(2)若点B,C在DE的两侧(如图②),(1)中的其他条件不变,AB与AC仍垂直吗?若垂直,请给出证明;若不垂直,请说明理由.
图17
答案
1.AO APO H.L.
2.C [解析]
A选项,∵AC=A'C',∠C=∠C',BC=B'C',∴Rt△ABC≌Rt△A'B'C'(S.A.S.),故A选项不符合题意;
B选项,∵∠A=∠A',∠C=∠C',AB=A'B',
∴Rt△ABC≌Rt△A'B'C'(A.A.S.),故B选项不符合题意;
C选项,∵AC=A'C',AB=A'B',∴Rt△ABC≌Rt△A'B'C'(H.L.),故C选项符合题意;
D选项,∵∠B=∠B',BC=B'C',∠C=∠C',∴Rt△ABC≌Rt△A'B'C'(A.S.A.),故D选项不符合题意.故选C.
3.EB=BD
4.证明:∵AC⊥BC,BD⊥AD,∴∠C=∠D=90°.
在Rt△ABC和Rt△BAD中,
∵AB=BA,AC=BD,
∴Rt△ABC≌Rt△BAD(H.L.).
5.C
6.40 [解析]
在Rt△ABC与Rt△DEF中,
∵AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(H.L.),
∴∠D=∠A=50°,
∴∠DFE=90°-∠D=90°-50°=40°.
7.证明:∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
∵BF=DE,∴BF+EF=DE+EF,
即BE=DF.
在Rt△AEB和Rt△CFD中,
∵AB=CD,BE=DF,
∴Rt△AEB≌Rt△CFD(H.L.),
∴∠B=∠D,∴AB∥CD.
8.解:在Rt△ABC与Rt△DEF中,
∵BC=EF,AC=DF,
∴Rt△ABC≌Rt△DEF(H.L.),
∴∠FED=∠CBA=32°(全等三角形的对应角相等),∴∠EFD=90°-32°=58°.
9.C [解析]
∵CD⊥AB,∠ECF=58°,
∴∠ADE=90°,∠DAC=32°.
∵EF⊥AC,
∴∠AFE=∠ADE=90°.
在Rt△ADE和Rt△AFE中,
∵AE=AE,DE=FE,
∴Rt△ADE≌Rt△AFE(H.L.),
∴∠DAE=∠FAE,
∴∠DAE=16°.故选C.
10.12
11.5或10
12.解:(1)3对,分别是△ABD≌△ACD,△ADE≌△ADF,△BDE≌△CDF.
(2)答案不唯一,选证△BDE≌△CDF.
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵D是BC的中点,∴BD=CD.
在Rt△BDE和Rt△CDF中,
∵BE=CF,BD=CD,
∴Rt△BDE≌Rt△CDF(H.L.).
13.证明:(1)∵BE⊥CD,
∴∠BEC=∠DEA=90°.
在Rt△BEC和Rt△DEA中,
∵BE=DE,BC=DA,
∴Rt△BEC≌Rt△DEA(H.L.).
(2)∵Rt△BEC≌Rt△DEA,∴∠B=∠D.
∵∠B+∠C=90°,∴∠C+∠D=90°,
∴∠DFC=90°,即DF⊥BC.
14.解:(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠CEA=90°.
在Rt△ABD和Rt△CAE中,
∵AB=CA,AD=CE,
∴Rt△ABD≌Rt△CAE,∴∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,
∴∠DAB+∠EAC=90°,
∴∠BAC=180°-(∠DAB+∠EAC)=90°,
∴AB⊥AC.
(2)AB与AC仍垂直.
证明:同(1)一样可证得Rt△ABD≌Rt△CAE,
∴∠DAB=∠ECA.
∵∠EAC+∠ECA=90°,
∴∠EAC+∠DAB=90°,即∠BAC=90°,
∴AB⊥AC.
【基础练习】
知识点
1 “H.L.”定理
1.如图4,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,公共边AO=
,则Rt△ADO≌Rt△ ,理由是 .?
图4
2.如图5,能用“H.L.”判定Rt△ABC和Rt△A'B'C'全等的条件是( )
图5
A.AC=A'C',BC=B'C'
B.∠A=∠A',AB=A'B'
C.AC=A'C',AB=A'B'
D.∠B=∠B',BC=B'C'
3.如图6,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件: ,从而可以根据“H.L.”判定Rt△EAB≌Rt△BCD.?
图6
4.如图7,已知AC⊥BC,BD⊥AD,AC与BD交于点O,AC=BD.求证:△ABC≌△BAD.
图7
知识点
2 “H.L.”定理的应用
5.如图8,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BCA=55°,则∠BCD的度数为( )
图8
A.145°
B.130°
C.110°
D.70°
6.如图9,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,∠A=50°,则∠DFE= °.?
图9
7.如图10,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE.求证:AB∥CD.
图10
8.如图11,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,∠CBA=32°,求∠EFD的度数.
图11
【能力提升】
9.[2019·哈尔滨呼兰区期中]
如图12,在△ABC中,CD⊥AB于点D,E为CD上一点,EF⊥AC于点F,连结AE.若ED=EF,∠ECF=58°,则∠DAE的度数为( )
图12
A.32°
B.18°
C.16°
D.29°
10.如图13,D为Rt△ABC中斜边BC上的一点,且BD=AB,过点D作BC的垂线,交AC于点E.若AE=12
cm,则DE的长为 cm.?
图13
11.如图14所示,在Rt△ABC中,∠C=90°,AC=10,BC=5,一条线段PQ=AB,点P,Q分别在AC和过点A且垂直于AC的射线AX上运动,当AP= 时,△ABC与△APQ全等.?
图14
12.如图15,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
(1)图中有几对全等的三角形?请一一列出;
(2)选择一对你认为全等的三角形进行证明.
图15
13.已知:如图16所示,BE⊥CD于点E,BE=DE,A为BE上一点,且BC=DA,DA的延长线交BC于点F.
求证:(1)△BEC≌△DEA;
(2)DF⊥BC.
图16
14.如图17,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)若点B,C在DE的同侧(如图①),且AD=CE,求证:AB⊥AC.
(2)若点B,C在DE的两侧(如图②),(1)中的其他条件不变,AB与AC仍垂直吗?若垂直,请给出证明;若不垂直,请说明理由.
图17
答案
1.AO APO H.L.
2.C [解析]
A选项,∵AC=A'C',∠C=∠C',BC=B'C',∴Rt△ABC≌Rt△A'B'C'(S.A.S.),故A选项不符合题意;
B选项,∵∠A=∠A',∠C=∠C',AB=A'B',
∴Rt△ABC≌Rt△A'B'C'(A.A.S.),故B选项不符合题意;
C选项,∵AC=A'C',AB=A'B',∴Rt△ABC≌Rt△A'B'C'(H.L.),故C选项符合题意;
D选项,∵∠B=∠B',BC=B'C',∠C=∠C',∴Rt△ABC≌Rt△A'B'C'(A.S.A.),故D选项不符合题意.故选C.
3.EB=BD
4.证明:∵AC⊥BC,BD⊥AD,∴∠C=∠D=90°.
在Rt△ABC和Rt△BAD中,
∵AB=BA,AC=BD,
∴Rt△ABC≌Rt△BAD(H.L.).
5.C
6.40 [解析]
在Rt△ABC与Rt△DEF中,
∵AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(H.L.),
∴∠D=∠A=50°,
∴∠DFE=90°-∠D=90°-50°=40°.
7.证明:∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
∵BF=DE,∴BF+EF=DE+EF,
即BE=DF.
在Rt△AEB和Rt△CFD中,
∵AB=CD,BE=DF,
∴Rt△AEB≌Rt△CFD(H.L.),
∴∠B=∠D,∴AB∥CD.
8.解:在Rt△ABC与Rt△DEF中,
∵BC=EF,AC=DF,
∴Rt△ABC≌Rt△DEF(H.L.),
∴∠FED=∠CBA=32°(全等三角形的对应角相等),∴∠EFD=90°-32°=58°.
9.C [解析]
∵CD⊥AB,∠ECF=58°,
∴∠ADE=90°,∠DAC=32°.
∵EF⊥AC,
∴∠AFE=∠ADE=90°.
在Rt△ADE和Rt△AFE中,
∵AE=AE,DE=FE,
∴Rt△ADE≌Rt△AFE(H.L.),
∴∠DAE=∠FAE,
∴∠DAE=16°.故选C.
10.12
11.5或10
12.解:(1)3对,分别是△ABD≌△ACD,△ADE≌△ADF,△BDE≌△CDF.
(2)答案不唯一,选证△BDE≌△CDF.
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵D是BC的中点,∴BD=CD.
在Rt△BDE和Rt△CDF中,
∵BE=CF,BD=CD,
∴Rt△BDE≌Rt△CDF(H.L.).
13.证明:(1)∵BE⊥CD,
∴∠BEC=∠DEA=90°.
在Rt△BEC和Rt△DEA中,
∵BE=DE,BC=DA,
∴Rt△BEC≌Rt△DEA(H.L.).
(2)∵Rt△BEC≌Rt△DEA,∴∠B=∠D.
∵∠B+∠C=90°,∴∠C+∠D=90°,
∴∠DFC=90°,即DF⊥BC.
14.解:(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠CEA=90°.
在Rt△ABD和Rt△CAE中,
∵AB=CA,AD=CE,
∴Rt△ABD≌Rt△CAE,∴∠DBA=∠EAC.
∵∠DAB+∠DBA=90°,
∴∠DAB+∠EAC=90°,
∴∠BAC=180°-(∠DAB+∠EAC)=90°,
∴AB⊥AC.
(2)AB与AC仍垂直.
证明:同(1)一样可证得Rt△ABD≌Rt△CAE,
∴∠DAB=∠ECA.
∵∠EAC+∠ECA=90°,
∴∠EAC+∠DAB=90°,即∠BAC=90°,
∴AB⊥AC.
