2020-2021学年人教版九年级数学上册课件: 21.3 实际问题与一元二次方程(81张)
文档属性
| 名称 | 2020-2021学年人教版九年级数学上册课件: 21.3 实际问题与一元二次方程(81张) |  | |
| 格式 | pptx | ||
| 文件大小 | 649.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-30 11:03:31 | ||
图片预览











文档简介
实际问题与一元二次方程
能根据实际问题中的数量关系,正确列出一元二次方程.?
通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识.
教学目标
教学重点
教学难点
正确列出一元二次方程,解决有关的实际问题.
根据实际问题列出一元二次方程.
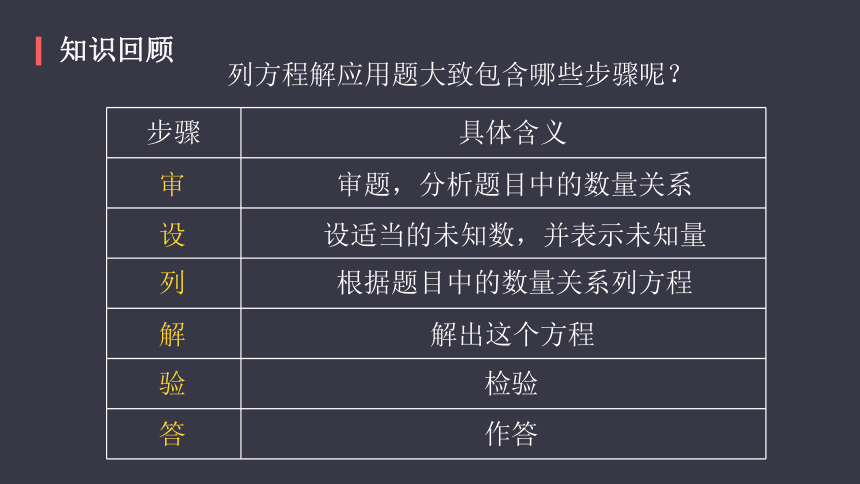
列方程解应用题大致包含哪些步骤呢?
知识回顾
步骤
审
设
列
解
验
答
具体含义
审题,分析题目中的数量关系
设适当的未知数,并表示未知量
根据题目中的数量关系列方程
解出这个方程
检验
作答
探究
若一人患流感每轮能传染5人,??
第二轮过后共有____________人患了流感.
则第一轮过后共有________人患了流感,
1+5
1+5+6×5
有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个人?
分析:不妨假设每轮传染中平均一个人传染了x个人.
第一轮
第二轮
一共有________人被传染.?
传染源有__________人.?
新增了____________人被传染.?
所以一共有_________________人被传染.?
1+x
x(1+x)
1+x+x(1+x)
探究
1+x
列方程
有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了x个人.
第一轮
第二轮
一共有________人被传染.?
1+x
探究
一共有__________________人被传染.?
答:
每轮传染中平均一个人传染了10个人.
1+x+x(1+x)
1+x+x(1+x)=121?
思考
有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个人?
每轮传染中平均一个人传染了10个人
如果按照这样的传染速度,
第三轮传染后有____________________人患流感.
1210+121=1331
前三轮被传染的总人数分别是11,121,1331
你能发现什么规律吗?
11,121=11?,1331=11??
后一轮是在前一轮的基础上乘以________
11
利用这个规律,你能换种方式列方程,
解决刚才的问题吗?
思考
另一种方式
列方程
有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了x个人.
第一轮
第二轮
一共有________人被传染.?
1+x
一共有______________________________人被传染.?
答:
每轮传染中平均一个人传染了10个人.
1+x+x(1+x)=(1+x)??
(1+x)?=121?
传播问题的规律
如果一开始是1个人,每轮传染中平均一个人传染x个人.?
第一轮
第二轮
第三轮
第四轮
第n轮
一共有________人被传染
一共有__________人被传染
一共有__________人被传染
一共有__________人被传染
一共有__________人被传染
归纳总结
……
……
1+x
(1+x)?
(1+x)?
(1+x)
(1+x)
某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是 91,每个支干长出多少个小分支?
练习
解:设每个支干长 x 个小分支,
由题意可得,1+x+x?=91
答:每个支干长出 9 个小分支.
去年的产量为5万吨,今年比去年增长了20%,今年的产量是多少?
今年比去年增长了20%,应理解为:
知识回顾
今年是去年的_________倍
所以:今年的产量 = 去年的产量× (1+20%)
(1+20%)
一件价格为200元的商品连续两次降价,每次降价的百分数为15%,降价后的商品价格是多少?
分析:第一次降价后的商品价格为原来的(1-15%)倍,
即 第一次为200×(1-15%),
第二次为第一次的(1-15%)倍,
即第二次为200×(1-15)×(1-15%)= 200 ×(1-15%)??
知识回顾
某农户的粮食产量年平均增长率为 x,?
问题1
第三年的产量为______________ kg.
第二年的产量为____________ kg,
第一年的产量为 60000 kg,
60000(1+x)
60000(1+x)??
某糖厂 2012 年食糖产量为 a 吨,??
问题2
2014 年的产量将是__________.
那么预计 2013 年的产量将是________.
如果在以后两年平均减产的百分率为 x,
a(1-x)
a(1-x)??
你能归纳上述两个问题中蕴含的共同等量关系吗?
归纳
两年后
变化后的量=变化前的量× _______________
(1±x)??
(其中增长取+,降低取-)
两年前生产1t 甲种药品的成本是5000元,生产1t 乙种药品的成本是6000 元,随着生产技术的进步,现在生产1t 甲种药品的成本是3000 元,生产1t 乙种药品的成本是3600 元,哪种药品成本的年平均下降率较大?
探究
年平均下降率的计算相对复杂,你能算出年平均下降额吗?
甲药品成本的年平均下降额:
(5000-3000)÷2=1000元
乙药品成本的年平均下降额:
(6000-3600)÷2=1200元
很显然,甲、乙的年平均下降额不同.
两年前生产1t 甲种药品的成本是5000元,
现在生产1t 甲种药品的成本是3000 元,
①求甲药品成本的年平均下降率
解:设甲药品成本的年平均下降率x,
一年后甲种药品成本为5000(1-x)元,
两年后甲种药品成本为5000(1-x)?元,
列方程,得:
5000(1-x)? = 3000
解方程,得:
探究
思考
两年前生产1t 甲种药品的成本是5000元,
现在生产1t 甲种药品的成本是3000 元,
解方程,得:
(舍去)
根据问题的实际意义可知,
成本下降率得是一个小于1的正数.
这两个解都
满足要求吗?
所以 x 只能取0.225,
即甲药品成本的年平均下降率为22.5%.
你能用类似的方法求出乙药品成本的年平均下降率吗?
探究
两年前生产1t 乙种药品的成本是6000 元,
现在生产1t 乙种药品的成本是3600 元,
②求乙药品成本的年平均下降率
解:设乙药品成本的年平均下降率y,
一年后乙种药品成本为6000(1-y)元,
两年后乙种药品成本为6000(1-y)?元,
列方程,得:
6000(1-y)? = 3600
解方程,得:
乙药品成本的年平均下降率为22.5%.
(舍去)
下降额大的药品,下降率一定大吗?
不一定
下降额反映的是绝对变化量,
下降率反映的是相对变化量,
两者兼顾才能全面比较对象的变化状况.
思考
药品
年平均下降额
年平均下降率
甲
乙
1000元
1200元
22.5%
22.5%
变化率问题
基本特征
平均变化率保持不变
关键步骤
①找出变化前后的数量
②找出等量关系
③根据等量关系列方程
归纳
某房屋开发公司经过几年的不懈努力,开发建设住宅面积由2000年4万平方米,到2002年的7万平方米.设这两年该房屋开发公司开发建设住宅面积的年平均增长率为x ,则可列方程为________________.
4(1+x)?=7
某彩电厂今年每个月的产量的增长率都相同.已知该厂今年4月份的彩电产量为5万台,6月份的产量为7.2万台.求月增长率.
答案:20%.
甲商场3月份的利润为200万元,5月份的利润为242万元. 求甲商场的月平均利润率?
答案:10%.
乙商场3月份的利润为100万元,5月份的利润为144万元.
求乙商场的月平均利润率?
答案:20%.
青山村种的水稻2007年平均每公顷8000kg,2009年平均每公顷产9680kg,求该村水稻每公顷产量的年平均增长率.
答案:10%.
某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,该校这两年实验器材投资上的平均增长率为多少?
提示: 2(1+x)+2(1+x)?=8 .
长沙市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备一开盘均价购买一套100平方米的房子.开发商还给予以下两种优惠方案以供选择:
①打9.8折销售;②不打折,送两年物业管理费,物业管理费是每平方米每月1.5元.请问哪种方案更优惠?
答案: (1)10% ;(2)方案1.
某工程队在城市实施棚户区改造过程中承包了一项拆迁工程,原计划每天拆迁1250平方米,因准备工作不足,第一天少拆迁了20%.从第二天开始,该工程队加快了拆迁速度,第三天拆迁了1440平方米.
(1)求该工程队第一天拆迁的面积?
(2)若该工程队第二天,第三天每天的拆迁面积比前一天的拆迁面积增长的百分数相同,求这个百分数 .
答案: (1)1000 ;(2)20%.
问题1
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下、左、右边衬等宽,应如何设计四周边衬的宽度?
解:可设四周边衬的宽度为 x cm,则中央矩形的面积可以
表示_______________________cm?.
根据边衬面积,可列方程:
还有其他列方程的方法吗?
(27-2x)(21-2x)
也可以直接根据中央矩形面积列方程:
问题1
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下、左、右边衬等宽,应如何设计四周边衬的宽度?
解:可设四周边衬的宽度为 x cm,则中央矩形的面积可以
表示_______________________cm?.
(27-2x)(21-2x)
总结:这类问题都可以用未知数表示边长,
然后利用边长与面积的关系列方程.
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位) ?
问题2
分析:封面的长宽之比是9∶7,
所以中央的矩形的长宽之比也应是______.
设中央的矩形的长和宽分别是 9a cm和 7a cm,
由此得上、下边衬与左、右边衬的宽度之比是:
= 9∶7?
9∶7
解:设上、下边衬的宽均为 9y cm,左、右边衬宽均为 7y cm,
则中央矩形的长为_________cm,中央矩形的宽_________cm.
问题2
根据中央矩形的面积可列方程:
整理得
解方程得:
(27-18y)
(21-14y)
这两个根都满足要求吗?
问题2
这显然不符合实际情况
所以上下边衬的宽为0.2×9=1.8cm
左右边衬的宽为0.2×7=1.4cm
刚才我们是设边衬的宽为未知数,然后列方程求解的,那有没有更简单的方法呢?
问题2
可以直接设中央矩形的长和宽,
然后列方程求出长和宽,再间接地求出边衬的宽度.
解:设中央矩形的长是9x,宽是7x,
依题意,得:
解方程,得:
接下来怎么求边衬的宽度呢?
(舍去)
上、下边衬的宽度为:
问题2
左、右边衬的宽度为:
1.8cm
1.4cm
面积问题
①设未知数
②把矩形的边长表示出来
③根据面积列方程
关键步骤
归纳
在长方形钢片上冲去一个长方形,制成一个四周宽相等的长方形框.已知长方形钢片的长为30cm,宽为20cm,要使制成的长方形框的面积为400cm?,求这个长方形框的框边宽.
答案:5cm.
如图,长方形ABCD,AB=15m,BC=20m,四周外围环绕着宽度相等的小路,已知小路的面积为246m?,求小路的宽度.
答案:3m.
如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?
答案:1m.
用20cm长的铁丝能否折成面积为30cm?的矩形,若能够,求它的长与宽;若不能,请说明理由.
已知矩形周长和面积求长和宽
答案:不能.
如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为 640 的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏 AB 的长为 x m,则根据题意可列方程_______________.
已知矩形周长和面积求长和宽
如图,有长为 22 米的篱笆,一面利用墙(墙的最大可用长度为?14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在 BC 上用其他材料造了宽为 1 米的两个小门.
?(1) 设花圃的宽 AB 为 x 米,请你用含 x 的代数式表示 BC 的长____________米;
?(2) 若此时花圃的面积刚好为 45 m ,
求此时花圃的宽.
已知矩形周长和面积求长和宽
答案:(1)(24-3x)米;(2)5米.
学校组织了一次篮球单循环比赛(每两队之间都进行了一次比赛),共进行了15场比赛,那么有几个球队参加了这次比赛?
比赛问题
答案:6.
参加足球联赛的每两队之间都进行了两次比赛(双循环比赛),共要比赛90场,共有多少个队参加了比赛?
比赛问题
答案:10.
两个连续奇数的积是 323,求这两个数?
数字问题
答案:17,19 或 -17,-19.
定价问题
百佳超市将进货单价为40元的商品按50元出售时,能卖500个,已知该商品要涨价1元,其销售量就要减少10个,为了赚8000元利润,售价应定为多少,这时应进货为多少个?
提示:设涨价 x 元,
然后把每件商品的利润和销量表示出来.
答案:要想赚8000元,售价为60元或80元;
若售价为60元,则进贷量应为400个;
若售价为80元,则进贷量应为200个.
定价问题
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天可多售出2件,若商场平均每天要盈利1200元,每件衬衫应降价多少元?
提示:设降价 x 元,
然后把每件衬衫的利润和销量表示出来.
答案:每件衬衫应降价20元.
定价问题
某商场将每件进价 80 元的某种商品原来按每件100元出售,一天可售出 100 件,后来经过市场调查,发现这种商品单价每降低?
1 元,其销售量可增加 10 件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)若商场经营该商品一天要获利润 2160 元,则每件商品应降价多少元?
答案:(1)利润2000元;(2)每件商品应降价2元或8元.
定价问题
新华商场销售某种冰箱,每台进价为2500元.市场调研表明:
当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
答案:2750元.
定价问题
某种新品种进价是120元,在试销阶段发现每件售价(元)与产品的日销售量(件)始终存在下表中的数量关系:
(1)请你根据上表中所给数据表述出每件售价提高的数量(元)与日销售量减少的数量(件)之间的关系.
(2)在不改变上述关系的情况下,请你帮助商场经理策划每件商品定价为多少元时,每日盈利可达到1600元?
答案:(1)每提高一元,销售量减少1个.(2)160元.
每件售(元)
每日销售(件)
130
70
150
50
165
35
这节课我们学会了什么?
1.传播问题的规律:
标题
如果一开始是1个人,每轮传染中平均一个人传染x个人.?
第n轮,一共有___________人被传染.?
(1+x)
2.变化率问题的求解步骤:
①找出变化前后的数量
②找出等量关系
③根据等量关系列方程
3.面积问题的求解步骤:
①设未知数
②把矩形的边长表示出来
③根据面积列方程
复习巩固
1. 解下列方程:
复习巩固
2. 两个相邻偶数的积是168. 求这两个偶数.
复习巩固
3. 一个直角三角形的两条直角边的和是14cm,面积是24cm?.求两条直角边的长.
综合运用
4. 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少小分支?
综合运用
5. 一个菱形两条对角线长的和是10cm,面积是12cm?.求菱形的周长.
综合运用
6. 参加足球联赛的每两队之间都进行两场比赛,共要比赛90场,共有多少个队参加比赛?
综合运用
7. 青山村种的水稻2010年平均每公顷产7200kg,2012年平均每公顷产8450kg.求水稻每公顷产量的年平均增长率.
综合运用
8. 要为一幅长29cm,宽22cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的四分之一,镜框边的宽度应是多少厘米(结果保留小数点后一位)?
拓广探索
9. 如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,横、竖彩条的宽度比为3:2.如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度(结果保留小数点后一位)?
拓广探索
10. 如图,线段 AB 的长为1.
A
B
C
D
E
三角点阵中前n行的点数计算
? ? ? ? 容易发现,10是三角点阵中前4行的点数和,你能发现300是前多少行的点数的和吗?
三角点阵中前n行的点数计算
? ? ? ? 用试验的方法,由上而下地逐行相加其点数,可以得到答案.但是这样寻找答案需要花费较多时间.你能用一元二次方程解决这个问题吗?
? ? ? ?三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
三角点阵中前n行的点数计算
? ? ? ? 如果把图1的三角点阵中各行的点数依次换为2,4,6,…,2n,…,你能探究出前n行的点数和满足什么规律吗?这个三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
复习巩固
1. 解下列方程:
(1)196x?-1=0;? ? ? ? ? ? ? ? ?(2)4x?+12x+9=81;
(3)x?-7x-1=0;? ? ? ? ? ? ? ? (4)2x?+3x=3;
(5)x?-2x+1=25;? ? ? ? ? ? ? (6)x(2x-5)=4x-10;
(7)x?+5x+7=3x+11;? ? ? ?(8)1-8x+16x?=2-8x.
复习巩固
2. 两个数的和为8,积为9.75. 求这两个数.
复习巩固
3. 一个矩形的长和宽相差3cm,面积是4cm?.求这个矩形的长和宽.
复习巩固
4. 求下列方程两个根的和与积:
(1)x?-5x-10=0;? ? ? ? ? ? ?(2)2x?+7x+1=0;?
(3)3x?-1=2x+5;? ? ? ? ? ? ?(4)x(x-1)=3x+7.
综合运用
5. 一个直角梯形的下底比上底长2cm,高比上底短1cm,面积是8cm?.画出这个梯形.
综合运用
6. 一个长方体的长与宽的比为5:2,高为5cm,表面积为40cm?.画出这个长方体的展开图.
综合运用
7. 要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛,应邀请多少个球队参加比赛?
综合运用
8. 如图,利用一面墙(墙的长度不限),用20cm长的篱笆,怎样围成一个面积为50cm?的矩形场地?
综合运用
9. 某银行经过最近的两次降息,使一年期存款的年利率由2.25%降至1.98%,平均每次降息的百分率是多少(结果写成a%的形式,其中a保留小数点后两位)?
综合运用
10. 向阳村2010年的人均收入为12000元,2012年的人均收入为14520元.求人均收入的年平均增长率.
综合运用
11. 用一条长40cm的绳子怎样围成一个面积为75cm?的矩形?能围成一个面积为101cm?的矩形吗?如能,说明围法;如不能,说明理由.
拓广探索
12. 如图,要设计一个等腰梯形的花坛,花坛上底长100m,下底长180m,上下底相距80m.在两腰中点连线处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.甬道的面积是梯形面积的六分之一.甬道的宽应是多少米(结果保留小数点后两位)?
拓广探索
13. 一个小球以 5m/s 的速度开始向前滚动,并且均匀减速,4s 后小球停止滚动.
(1)小球的滚动速度平均每秒减少多少?
(2)小球滚动 5m 约用了多少秒(结果保留小数点后一位)?
(提示:匀变速直线运动中,每个时间段内的平均速度 v(初速度与末速度的算术平均数)与路程 s ,时间 t 的关系为 s=vt .)
能根据实际问题中的数量关系,正确列出一元二次方程.?
通过列方程解应用题体会一元二次方程在实际生活中的应用,经历将实际问题转化为数学问题的过程,提高数学应用意识.
教学目标
教学重点
教学难点
正确列出一元二次方程,解决有关的实际问题.
根据实际问题列出一元二次方程.
列方程解应用题大致包含哪些步骤呢?
知识回顾
步骤
审
设
列
解
验
答
具体含义
审题,分析题目中的数量关系
设适当的未知数,并表示未知量
根据题目中的数量关系列方程
解出这个方程
检验
作答
探究
若一人患流感每轮能传染5人,??
第二轮过后共有____________人患了流感.
则第一轮过后共有________人患了流感,
1+5
1+5+6×5
有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个人?
分析:不妨假设每轮传染中平均一个人传染了x个人.
第一轮
第二轮
一共有________人被传染.?
传染源有__________人.?
新增了____________人被传染.?
所以一共有_________________人被传染.?
1+x
x(1+x)
1+x+x(1+x)
探究
1+x
列方程
有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了x个人.
第一轮
第二轮
一共有________人被传染.?
1+x
探究
一共有__________________人被传染.?
答:
每轮传染中平均一个人传染了10个人.
1+x+x(1+x)
1+x+x(1+x)=121?
思考
有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个人?
每轮传染中平均一个人传染了10个人
如果按照这样的传染速度,
第三轮传染后有____________________人患流感.
1210+121=1331
前三轮被传染的总人数分别是11,121,1331
你能发现什么规律吗?
11,121=11?,1331=11??
后一轮是在前一轮的基础上乘以________
11
利用这个规律,你能换种方式列方程,
解决刚才的问题吗?
思考
另一种方式
列方程
有一个人患了流感,经过两轮传染后共有 121个人患了流感,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了x个人.
第一轮
第二轮
一共有________人被传染.?
1+x
一共有______________________________人被传染.?
答:
每轮传染中平均一个人传染了10个人.
1+x+x(1+x)=(1+x)??
(1+x)?=121?
传播问题的规律
如果一开始是1个人,每轮传染中平均一个人传染x个人.?
第一轮
第二轮
第三轮
第四轮
第n轮
一共有________人被传染
一共有__________人被传染
一共有__________人被传染
一共有__________人被传染
一共有__________人被传染
归纳总结
……
……
1+x
(1+x)?
(1+x)?
(1+x)
(1+x)
某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是 91,每个支干长出多少个小分支?
练习
解:设每个支干长 x 个小分支,
由题意可得,1+x+x?=91
答:每个支干长出 9 个小分支.
去年的产量为5万吨,今年比去年增长了20%,今年的产量是多少?
今年比去年增长了20%,应理解为:
知识回顾
今年是去年的_________倍
所以:今年的产量 = 去年的产量× (1+20%)
(1+20%)
一件价格为200元的商品连续两次降价,每次降价的百分数为15%,降价后的商品价格是多少?
分析:第一次降价后的商品价格为原来的(1-15%)倍,
即 第一次为200×(1-15%),
第二次为第一次的(1-15%)倍,
即第二次为200×(1-15)×(1-15%)= 200 ×(1-15%)??
知识回顾
某农户的粮食产量年平均增长率为 x,?
问题1
第三年的产量为______________ kg.
第二年的产量为____________ kg,
第一年的产量为 60000 kg,
60000(1+x)
60000(1+x)??
某糖厂 2012 年食糖产量为 a 吨,??
问题2
2014 年的产量将是__________.
那么预计 2013 年的产量将是________.
如果在以后两年平均减产的百分率为 x,
a(1-x)
a(1-x)??
你能归纳上述两个问题中蕴含的共同等量关系吗?
归纳
两年后
变化后的量=变化前的量× _______________
(1±x)??
(其中增长取+,降低取-)
两年前生产1t 甲种药品的成本是5000元,生产1t 乙种药品的成本是6000 元,随着生产技术的进步,现在生产1t 甲种药品的成本是3000 元,生产1t 乙种药品的成本是3600 元,哪种药品成本的年平均下降率较大?
探究
年平均下降率的计算相对复杂,你能算出年平均下降额吗?
甲药品成本的年平均下降额:
(5000-3000)÷2=1000元
乙药品成本的年平均下降额:
(6000-3600)÷2=1200元
很显然,甲、乙的年平均下降额不同.
两年前生产1t 甲种药品的成本是5000元,
现在生产1t 甲种药品的成本是3000 元,
①求甲药品成本的年平均下降率
解:设甲药品成本的年平均下降率x,
一年后甲种药品成本为5000(1-x)元,
两年后甲种药品成本为5000(1-x)?元,
列方程,得:
5000(1-x)? = 3000
解方程,得:
探究
思考
两年前生产1t 甲种药品的成本是5000元,
现在生产1t 甲种药品的成本是3000 元,
解方程,得:
(舍去)
根据问题的实际意义可知,
成本下降率得是一个小于1的正数.
这两个解都
满足要求吗?
所以 x 只能取0.225,
即甲药品成本的年平均下降率为22.5%.
你能用类似的方法求出乙药品成本的年平均下降率吗?
探究
两年前生产1t 乙种药品的成本是6000 元,
现在生产1t 乙种药品的成本是3600 元,
②求乙药品成本的年平均下降率
解:设乙药品成本的年平均下降率y,
一年后乙种药品成本为6000(1-y)元,
两年后乙种药品成本为6000(1-y)?元,
列方程,得:
6000(1-y)? = 3600
解方程,得:
乙药品成本的年平均下降率为22.5%.
(舍去)
下降额大的药品,下降率一定大吗?
不一定
下降额反映的是绝对变化量,
下降率反映的是相对变化量,
两者兼顾才能全面比较对象的变化状况.
思考
药品
年平均下降额
年平均下降率
甲
乙
1000元
1200元
22.5%
22.5%
变化率问题
基本特征
平均变化率保持不变
关键步骤
①找出变化前后的数量
②找出等量关系
③根据等量关系列方程
归纳
某房屋开发公司经过几年的不懈努力,开发建设住宅面积由2000年4万平方米,到2002年的7万平方米.设这两年该房屋开发公司开发建设住宅面积的年平均增长率为x ,则可列方程为________________.
4(1+x)?=7
某彩电厂今年每个月的产量的增长率都相同.已知该厂今年4月份的彩电产量为5万台,6月份的产量为7.2万台.求月增长率.
答案:20%.
甲商场3月份的利润为200万元,5月份的利润为242万元. 求甲商场的月平均利润率?
答案:10%.
乙商场3月份的利润为100万元,5月份的利润为144万元.
求乙商场的月平均利润率?
答案:20%.
青山村种的水稻2007年平均每公顷8000kg,2009年平均每公顷产9680kg,求该村水稻每公顷产量的年平均增长率.
答案:10%.
某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,该校这两年实验器材投资上的平均增长率为多少?
提示: 2(1+x)+2(1+x)?=8 .
长沙市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备一开盘均价购买一套100平方米的房子.开发商还给予以下两种优惠方案以供选择:
①打9.8折销售;②不打折,送两年物业管理费,物业管理费是每平方米每月1.5元.请问哪种方案更优惠?
答案: (1)10% ;(2)方案1.
某工程队在城市实施棚户区改造过程中承包了一项拆迁工程,原计划每天拆迁1250平方米,因准备工作不足,第一天少拆迁了20%.从第二天开始,该工程队加快了拆迁速度,第三天拆迁了1440平方米.
(1)求该工程队第一天拆迁的面积?
(2)若该工程队第二天,第三天每天的拆迁面积比前一天的拆迁面积增长的百分数相同,求这个百分数 .
答案: (1)1000 ;(2)20%.
问题1
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下、左、右边衬等宽,应如何设计四周边衬的宽度?
解:可设四周边衬的宽度为 x cm,则中央矩形的面积可以
表示_______________________cm?.
根据边衬面积,可列方程:
还有其他列方程的方法吗?
(27-2x)(21-2x)
也可以直接根据中央矩形面积列方程:
问题1
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下、左、右边衬等宽,应如何设计四周边衬的宽度?
解:可设四周边衬的宽度为 x cm,则中央矩形的面积可以
表示_______________________cm?.
(27-2x)(21-2x)
总结:这类问题都可以用未知数表示边长,
然后利用边长与面积的关系列方程.
要设计一本书的封面,封面长 27 cm,宽 21 cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度(结果保留小数点后一位) ?
问题2
分析:封面的长宽之比是9∶7,
所以中央的矩形的长宽之比也应是______.
设中央的矩形的长和宽分别是 9a cm和 7a cm,
由此得上、下边衬与左、右边衬的宽度之比是:
= 9∶7?
9∶7
解:设上、下边衬的宽均为 9y cm,左、右边衬宽均为 7y cm,
则中央矩形的长为_________cm,中央矩形的宽_________cm.
问题2
根据中央矩形的面积可列方程:
整理得
解方程得:
(27-18y)
(21-14y)
这两个根都满足要求吗?
问题2
这显然不符合实际情况
所以上下边衬的宽为0.2×9=1.8cm
左右边衬的宽为0.2×7=1.4cm
刚才我们是设边衬的宽为未知数,然后列方程求解的,那有没有更简单的方法呢?
问题2
可以直接设中央矩形的长和宽,
然后列方程求出长和宽,再间接地求出边衬的宽度.
解:设中央矩形的长是9x,宽是7x,
依题意,得:
解方程,得:
接下来怎么求边衬的宽度呢?
(舍去)
上、下边衬的宽度为:
问题2
左、右边衬的宽度为:
1.8cm
1.4cm
面积问题
①设未知数
②把矩形的边长表示出来
③根据面积列方程
关键步骤
归纳
在长方形钢片上冲去一个长方形,制成一个四周宽相等的长方形框.已知长方形钢片的长为30cm,宽为20cm,要使制成的长方形框的面积为400cm?,求这个长方形框的框边宽.
答案:5cm.
如图,长方形ABCD,AB=15m,BC=20m,四周外围环绕着宽度相等的小路,已知小路的面积为246m?,求小路的宽度.
答案:3m.
如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?
答案:1m.
用20cm长的铁丝能否折成面积为30cm?的矩形,若能够,求它的长与宽;若不能,请说明理由.
已知矩形周长和面积求长和宽
答案:不能.
如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为 640 的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏 AB 的长为 x m,则根据题意可列方程_______________.
已知矩形周长和面积求长和宽
如图,有长为 22 米的篱笆,一面利用墙(墙的最大可用长度为?14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在 BC 上用其他材料造了宽为 1 米的两个小门.
?(1) 设花圃的宽 AB 为 x 米,请你用含 x 的代数式表示 BC 的长____________米;
?(2) 若此时花圃的面积刚好为 45 m ,
求此时花圃的宽.
已知矩形周长和面积求长和宽
答案:(1)(24-3x)米;(2)5米.
学校组织了一次篮球单循环比赛(每两队之间都进行了一次比赛),共进行了15场比赛,那么有几个球队参加了这次比赛?
比赛问题
答案:6.
参加足球联赛的每两队之间都进行了两次比赛(双循环比赛),共要比赛90场,共有多少个队参加了比赛?
比赛问题
答案:10.
两个连续奇数的积是 323,求这两个数?
数字问题
答案:17,19 或 -17,-19.
定价问题
百佳超市将进货单价为40元的商品按50元出售时,能卖500个,已知该商品要涨价1元,其销售量就要减少10个,为了赚8000元利润,售价应定为多少,这时应进货为多少个?
提示:设涨价 x 元,
然后把每件商品的利润和销量表示出来.
答案:要想赚8000元,售价为60元或80元;
若售价为60元,则进贷量应为400个;
若售价为80元,则进贷量应为200个.
定价问题
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天可多售出2件,若商场平均每天要盈利1200元,每件衬衫应降价多少元?
提示:设降价 x 元,
然后把每件衬衫的利润和销量表示出来.
答案:每件衬衫应降价20元.
定价问题
某商场将每件进价 80 元的某种商品原来按每件100元出售,一天可售出 100 件,后来经过市场调查,发现这种商品单价每降低?
1 元,其销售量可增加 10 件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)若商场经营该商品一天要获利润 2160 元,则每件商品应降价多少元?
答案:(1)利润2000元;(2)每件商品应降价2元或8元.
定价问题
新华商场销售某种冰箱,每台进价为2500元.市场调研表明:
当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
答案:2750元.
定价问题
某种新品种进价是120元,在试销阶段发现每件售价(元)与产品的日销售量(件)始终存在下表中的数量关系:
(1)请你根据上表中所给数据表述出每件售价提高的数量(元)与日销售量减少的数量(件)之间的关系.
(2)在不改变上述关系的情况下,请你帮助商场经理策划每件商品定价为多少元时,每日盈利可达到1600元?
答案:(1)每提高一元,销售量减少1个.(2)160元.
每件售(元)
每日销售(件)
130
70
150
50
165
35
这节课我们学会了什么?
1.传播问题的规律:
标题
如果一开始是1个人,每轮传染中平均一个人传染x个人.?
第n轮,一共有___________人被传染.?
(1+x)
2.变化率问题的求解步骤:
①找出变化前后的数量
②找出等量关系
③根据等量关系列方程
3.面积问题的求解步骤:
①设未知数
②把矩形的边长表示出来
③根据面积列方程
复习巩固
1. 解下列方程:
复习巩固
2. 两个相邻偶数的积是168. 求这两个偶数.
复习巩固
3. 一个直角三角形的两条直角边的和是14cm,面积是24cm?.求两条直角边的长.
综合运用
4. 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少小分支?
综合运用
5. 一个菱形两条对角线长的和是10cm,面积是12cm?.求菱形的周长.
综合运用
6. 参加足球联赛的每两队之间都进行两场比赛,共要比赛90场,共有多少个队参加比赛?
综合运用
7. 青山村种的水稻2010年平均每公顷产7200kg,2012年平均每公顷产8450kg.求水稻每公顷产量的年平均增长率.
综合运用
8. 要为一幅长29cm,宽22cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的四分之一,镜框边的宽度应是多少厘米(结果保留小数点后一位)?
拓广探索
9. 如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,横、竖彩条的宽度比为3:2.如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度(结果保留小数点后一位)?
拓广探索
10. 如图,线段 AB 的长为1.
A
B
C
D
E
三角点阵中前n行的点数计算
? ? ? ? 容易发现,10是三角点阵中前4行的点数和,你能发现300是前多少行的点数的和吗?
三角点阵中前n行的点数计算
? ? ? ? 用试验的方法,由上而下地逐行相加其点数,可以得到答案.但是这样寻找答案需要花费较多时间.你能用一元二次方程解决这个问题吗?
? ? ? ?三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
三角点阵中前n行的点数计算
? ? ? ? 如果把图1的三角点阵中各行的点数依次换为2,4,6,…,2n,…,你能探究出前n行的点数和满足什么规律吗?这个三角点阵中前n行的点数和能是600吗?如果能,求出n;如果不能,试用一元二次方程说明道理.
复习巩固
1. 解下列方程:
(1)196x?-1=0;? ? ? ? ? ? ? ? ?(2)4x?+12x+9=81;
(3)x?-7x-1=0;? ? ? ? ? ? ? ? (4)2x?+3x=3;
(5)x?-2x+1=25;? ? ? ? ? ? ? (6)x(2x-5)=4x-10;
(7)x?+5x+7=3x+11;? ? ? ?(8)1-8x+16x?=2-8x.
复习巩固
2. 两个数的和为8,积为9.75. 求这两个数.
复习巩固
3. 一个矩形的长和宽相差3cm,面积是4cm?.求这个矩形的长和宽.
复习巩固
4. 求下列方程两个根的和与积:
(1)x?-5x-10=0;? ? ? ? ? ? ?(2)2x?+7x+1=0;?
(3)3x?-1=2x+5;? ? ? ? ? ? ?(4)x(x-1)=3x+7.
综合运用
5. 一个直角梯形的下底比上底长2cm,高比上底短1cm,面积是8cm?.画出这个梯形.
综合运用
6. 一个长方体的长与宽的比为5:2,高为5cm,表面积为40cm?.画出这个长方体的展开图.
综合运用
7. 要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛,应邀请多少个球队参加比赛?
综合运用
8. 如图,利用一面墙(墙的长度不限),用20cm长的篱笆,怎样围成一个面积为50cm?的矩形场地?
综合运用
9. 某银行经过最近的两次降息,使一年期存款的年利率由2.25%降至1.98%,平均每次降息的百分率是多少(结果写成a%的形式,其中a保留小数点后两位)?
综合运用
10. 向阳村2010年的人均收入为12000元,2012年的人均收入为14520元.求人均收入的年平均增长率.
综合运用
11. 用一条长40cm的绳子怎样围成一个面积为75cm?的矩形?能围成一个面积为101cm?的矩形吗?如能,说明围法;如不能,说明理由.
拓广探索
12. 如图,要设计一个等腰梯形的花坛,花坛上底长100m,下底长180m,上下底相距80m.在两腰中点连线处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.甬道的面积是梯形面积的六分之一.甬道的宽应是多少米(结果保留小数点后两位)?
拓广探索
13. 一个小球以 5m/s 的速度开始向前滚动,并且均匀减速,4s 后小球停止滚动.
(1)小球的滚动速度平均每秒减少多少?
(2)小球滚动 5m 约用了多少秒(结果保留小数点后一位)?
(提示:匀变速直线运动中,每个时间段内的平均速度 v(初速度与末速度的算术平均数)与路程 s ,时间 t 的关系为 s=vt .)
同课章节目录
